基于多源数据融合的采煤机截割载荷预测方法

于 宁 孙业新 陈洪月

辽宁工程技术大学机械工程学院，阜新，123000

0 引言

采煤机是煤矿开采最重要的设备。由于采煤工作面不均匀围岩、坚硬夹矸等因素的影响，采煤机滚筒在截割过程中易受到强烈的冲击，导致截割滚筒的截齿异常磨损或摇臂内的齿轮断齿失效等[1-2]，因此，研究采煤机的滚筒载荷识别与预测方法对采煤机工作状态监测与预警具有重要意义。

截割载荷预测在煤矿装备智能化领域一直是研究热点与难题。郝志勇等[3]通过实验采集销轴和压力环的三向应变，采用小波分解降噪并进行载荷谱分形关联维数计算，研究了滚筒截割载荷分布规律；李晓豁等[4]基于MATLAB/GUI研发了滚筒截割载荷模拟系统，依据滚筒参数和煤岩信息预测截割载荷，解决了截割载荷计算困难问题；刘春生等[5]提出了一种改进分数阶Tikhonov正则化载荷识别算法，对截割载荷有较好的识别效果。目前，有不少学者应用神经网络识别与预测截割载荷。张强等[6]提出一种基于模糊神经网络的多传感器信息融合的煤岩识别方法，依据实验提取截割过程中的振动、电流等信号特征，预测了滚筒的截割轨迹。刘春生等[7]建立了基于熵权的正则化神经网络载荷谱预测模型，提出了依据有限楔入角的载荷谱的预测方法，实现不同楔入角的截割载荷预测。蒋干[8]采用IFOA-RBF神经网络实现了单一传感信号下的煤岩截割状态识别，经过D-S证据理论融合，最终得到了煤岩截割载荷识别结果。毛君等[9]将深度信念网络(deep belief network，DBN)应用于滚筒载荷预测，经过实验测试得到了良好的载荷预测效果，结果表明DBN预测模型特征提取能力强，且优于BP神经网络(BPNN)。

综上所述，在数据量庞大且复杂的条件下，DBN可以实现特征自主学习，在预测精度上优于传统的神经网络，而应用DBN的载荷预测研究较少。在上述学者对截割载荷的研究基础上，本文提出了一种改进的DBN载荷预测模型，在DBN的基础上，结合贝叶斯正则化(BR)方法和粒子群优化(PSO)算法，建立了基于BR-PSO-DBN的滚筒载荷预测模型。

1 DBN的改进

1.1 DBN

DBN由多层无监督受限玻尔兹曼机(restricted Boltzmann machine，RBM)和一层有监督的反向传播网络堆叠而成[10]。DBN包含两个学习过程：前向无监督堆叠和后向有监督微调。前向无监督堆叠过程为：将第一个RBM的输出作为第二个RBM的输入，依此类推，采用贪婪学习算法进行预训练，实现从前到后的无监督学习，初步确定网络权重。后向有监督微调过程为：从DBN网络最后一层开始精调网络各层的参数，根据标签数据进行训练，采用BP算法微调初始网络权重，得到最优的网络参数。

1.2 引入BR法

多传感器采集条件下，数据量增大，特征维度增加，RBM堆叠得到的DBN非常复杂，建立的模型容易发生过拟合现象。为避免过拟合问题，增强网络的泛化能力，本文引入BR法优化每层RBM的训练函数，限制网络规模的同时减小训练误差。

根据BR法[11]，将RBM中的性能函数优化为

Fw=αP+βEw

(1)

(2)

P0=P(v,h)∝exp(-E(v,h))=
exp(hTWv+bTv+aTh)

(3)

式中，Fw为优化的训练函数；Ew为复杂度惩罚项；P0为初始的训练函数；α、β为超参数；h、v分别表示隐含层和可视层；m、n分别为可视单元与隐藏单元数量；P为联合概率分布；E(v,h)为该组态下的能量函数；W为显层与隐层各单元之间的连接权值，W=[wij]；a、b分别为显层与隐层各单元的偏置值。

如果α远大于β，则减小训练误差，如果α远小于β，则减小网络规模。

确定网络结构后，确定训练函数超参数α、β的取值。依据HINTON等[12]给出的正则化法超参数取值的经验(α∈[0.5,1]，β∈[0,0.5])，本文通过实验随机多次在取值范围内给α、β赋值，最后取网络识别效果最佳的赋值。引入BR法优化各层RBM，确定最优的网络模型规模以及超参数α、β，提高网络对样本数据的适应能力。

1.3 引入PSO算法

为使网络获得最优的网络权重，引入PSO算法对传统的BP算法加以改进，强化网络精调的能力。PSO算法通过随机粒子种群迭代进行寻优，每次迭代通过跟踪个体最优解和全局最优解来更新粒子的运行速度和位置。首先初始化粒子群参数，种群F={F1,F2,…,Fn}，设第i个粒子在t次迭代的位置为Fi,t=(fi1,t,fi2,t,…，fiD,t)T，速度Vi,t=(vi1,t,vi2,t,…,viD，t)T，个体的最优位置pi，t=(pi1，t,pi2，t,…,piD，t)T，全局的最优位置pg，t=(pg1，t,pg2，t,…,pgD，t)T，则第i粒子在t+1次迭代时有：

vid，t+1=vid，t+c1r1(pid，t-xid，t)+c2r2(pgd，t-xid，t)

(4)

式中，d=1,2,…，D；i=1,2,…,n；r1、r2为样本空间(0，1)内的随机数；c1、c2为加速因子。

PSO算法中如果个体最优解多于全局最优解，则会陷入局部最优解，所以笔者引入惯性权重来平衡算法的寻优能力：

w=wmax-(wmax-wmin)t/tmax

(5)

(6)

式中，w为第t次迭代的权重；C1、C2为第t次迭代的加速因子；wmax、wmin分别为最大和最小的惯性权重；tmax为最大迭代次数；Cmax、Cmin分别为最大和最小的加速因子。

式(5)能够增强算法局部寻优能力，式(6)能够增强粒子个体的搜索能力和对全局的感知能力。改进PSO算法的步骤如图1所示。

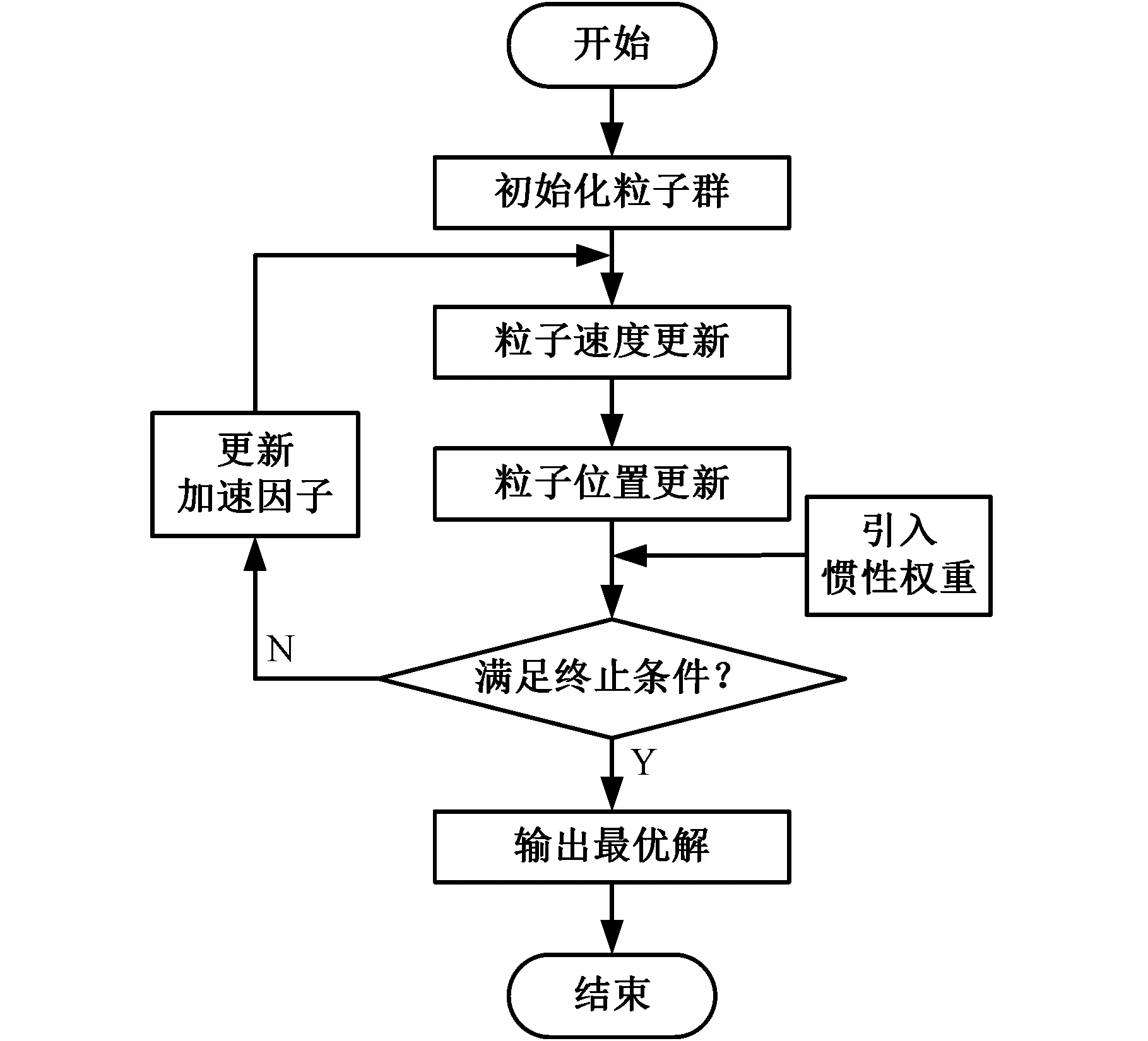
图1 改进粒子群算法步骤Fig.1 Steps of improved particle swarm algorithm

1.4 改进决策域更新系数

PSO算法是群智能算法之一，而收敛停滞一直是群智能算法的难题，因为算法有限的搜索能力，使种群可能收敛到一个停滞解[13]。为克服此问题，本文通过改进决策域更新系数来增大种群个体的决策域半径。

引入指数分布系数对决策域更新系数β0进行改进：

β′=β0Ri

(7)

式中,Ri为指数分布系数。

与原更新系数相比，指数分布系数扩大了算法的搜索范围，加快了起始计算速度，增强了局部寻优能力。

对引入指数分布系数的决策域更新系数做线性处理，以保证改进后的算法在后期的搜索精度：

β′(t)=β′min+(β′max-β′min)t/tmax

(8)

种群迭代至后期时，算法的调整步长减小，以实现最优解的搜索精度。

综合考虑算法的收敛速度和寻优精度，采用递减移动步长S，使算法整个过程始终保持较高的搜索强度，递减的公式为

S=S0δtεδ∈(0,1)

(9)

式中，S0为初始步长；δ为递减系数；ε为待优化问题的问题域。

改进后的动态决策域半径更新公式为

(10)

式中,rs为萤火虫感知域；rdi为萤火虫i的动态决策域；ni为邻域的阈值；Ni(t)为萤火虫i在第t次的邻居集合。

位置更新公式为

(11)

2 建立BR-PSO-DBN预测模型

本文以某型采煤机左截割部为实验对象，滚筒截割三向载荷和滚筒扭矩为预测目标，输入参数选取惰轮轴、连接架销轴载荷和摇臂壳体应变量，采煤机截割部结构见图2。

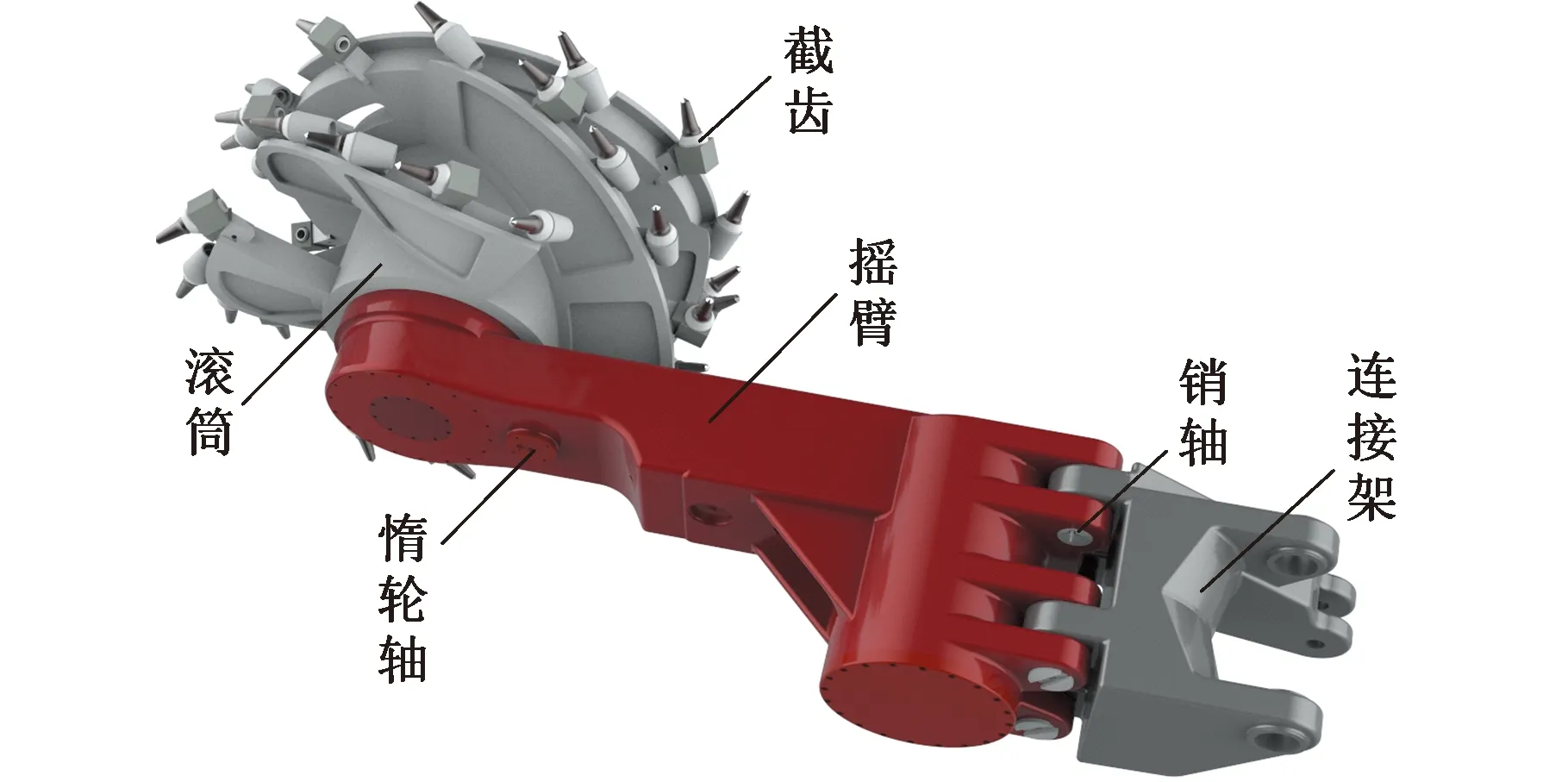
图2 采煤机截割部结构图Fig.2 Structure diagram of cutting part of coalmining machine

(1)惰轮轴载荷。惰轮轴距离滚筒侧最近，载荷传递损耗小，以惰轮轴载荷为特征参数，能够提高截割载荷预测精度。实验中采用与惰轮轴外形相似且具有同等力学特性的传感器[14]，实时监测截割过程中惰轮轴的Y向和Z向受力情况。

(2)连接架销轴载荷。连接架销轴连接摇臂与连接架，滚筒截割载荷通过摇臂作用在连接架销轴，因此连接架销轴载荷可以作为预测截割载荷的特征参数。4个连接销轴Y向和Z向受力状况由具有相同强度的销轴传感器测得[15]。

(3)摇臂壳体应变。摇臂作为截割部的重要组成部分，支撑整个滚筒，承受较大的滚筒截割载荷，所以在摇臂壳体两侧进行应力应变测量。利用模态分析方法[16]研究摇臂变形规律，在摇臂采空面过渡位置和惰轮轴周围的受力较大区域内布置12个应变传感器，并在应变传感器正上方安装金属防护板，以适应截割煤岩时的复杂工况。传感器布置如图3所示，其中3、5、8号传感器测量Z向应变，余下传感器测量Y向应变。

图3 摇臂壳体应变值采集示意图Fig.3 Schematic illustration of the collection of strainvalues of the rocker shell

将截割部滚筒所受三向截割载荷和扭矩作为输出参数，实测数据通过截齿传感器采集[17]。

综上所述，采煤机滚筒载荷预测模型的输入层包括22个神经元，输出层包括4个神经元。构建的BR-PSO-DBN模型如图4所示，其中，C表示隐含层， W表示对应计算过程。

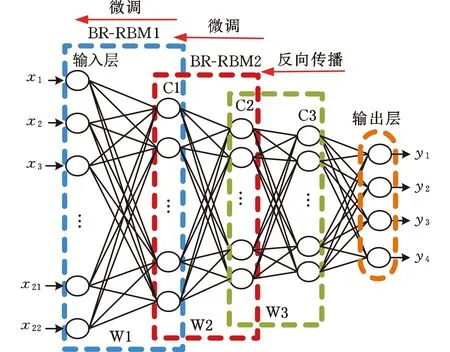
图4 BR-PSO-DBN预测模型Fig.4 BR-PSO-DBN forecasting model

BR-PSO-DBN预测模型包含2个BR-RBM隐含层，各隐含层内神经元个数由BR法优化确定；预测模型采用BP-PSO算法进行微调。

3 训练BR-PSO-DBN预测模型

在截割载荷预测之前，对BR-PSO-DBN预测模型进行训练。

(1)数据处理。从实验数据中提取输入样本并构建样本空间，划分训练样本和测试样本。样本空间根据3种不同工况分为3个部分，分别在各区域内中截取10 000个样本数据。归一化处理样本数据，加快程序的运行，公式为

x*=(x-xmin)/(xmax-xmin)

(12)

式中，xmin为样本数据最小值；xmax为样本数据最大值。

(2)数据融合。输入层xi通过2层RBM和1层反馈层进行数据融合，RBM作为一种生成式随机神经网络，其联合状态的能量函数为

(13)

式中，I、J分别为显性神经元和隐性神经元的个数。

RBM中隐层C1或C2中的神经元hj被激活的概率为

(14)

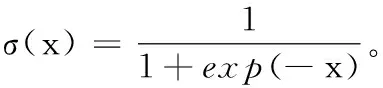
判断神经元hj是否被激活的公式为

(15)

式中，u服从0～1均匀分布，即u～U(0,1)。

RBM为双向连接，则重构时隐层神经元激活显层神经元的概率为

(16)

对反馈层采用BP算法，输出神经元表达式为

(17)

其权重表达式为

wji(t+1)=wji(t)+ηδpjopj

(18)

式中，η为微调学习速率；δpj为网络预测误差；opj为神经元的输出信号。

(3)无监督学习。通过贝叶斯法优化每层RBM的规模，固定隐元个数，确定超参数α、β和初始权值。预训练阶段学习速率采用常用值0.1，每个RBM迭代200次。

(4)有监督学习。输入标签数据通过PSO算法优化的BP神经网络微调,确定最优权值，微调学习速率η同样设置为0.1，最后保存训练好的网络模型参数。具体流程见图5。

图5 BR-PSO-DBN具体流程图Fig.5 BR-PSO-DBN specific flow chart

4 截割载荷测试实验

实验数据来源于中煤张家口煤矿机械装备实验室，模拟井下实际工况进行采煤机截割载荷实验测试，实验系统的组成如图6所示。

图6 实验系统Fig.6 Experimental system

实验系统通过在螺旋滚筒下方安装无线发射模块采集截齿传感器数据，在摇臂采空侧安装无线发射模块对惰轮轴传感器、摇臂应变等数据进行采集和无线传输，最后汇总显示到PC端。

根据截煤经验，采煤机摇臂割顶煤时比采煤机摇臂割底煤时更易发生应变集中而造成摇臂损伤，并且随摇臂摆角增大而显著，因此实验中，左截割部在摇臂最大摆角35°条件下，分别测试采煤机空载、斜切进刀和正常截割三种工况下不同速度时的受力。在采煤机空载阶段牵引速度设为2 m/min，检查采煤机行走过程中各传感数据传输情况；当采煤机行至26号架后以3 m/min行驶，进入斜切进刀截割过程；当采煤机行至16号架时，进入到正常截割阶段，采煤机以3 m/min继续截割至煤壁最左侧停止，实验经28 min结束，样本数据采集完毕。测试时三机状态如图7所示，测试过程严格按照采煤机在煤矿井下的截割工艺运作。

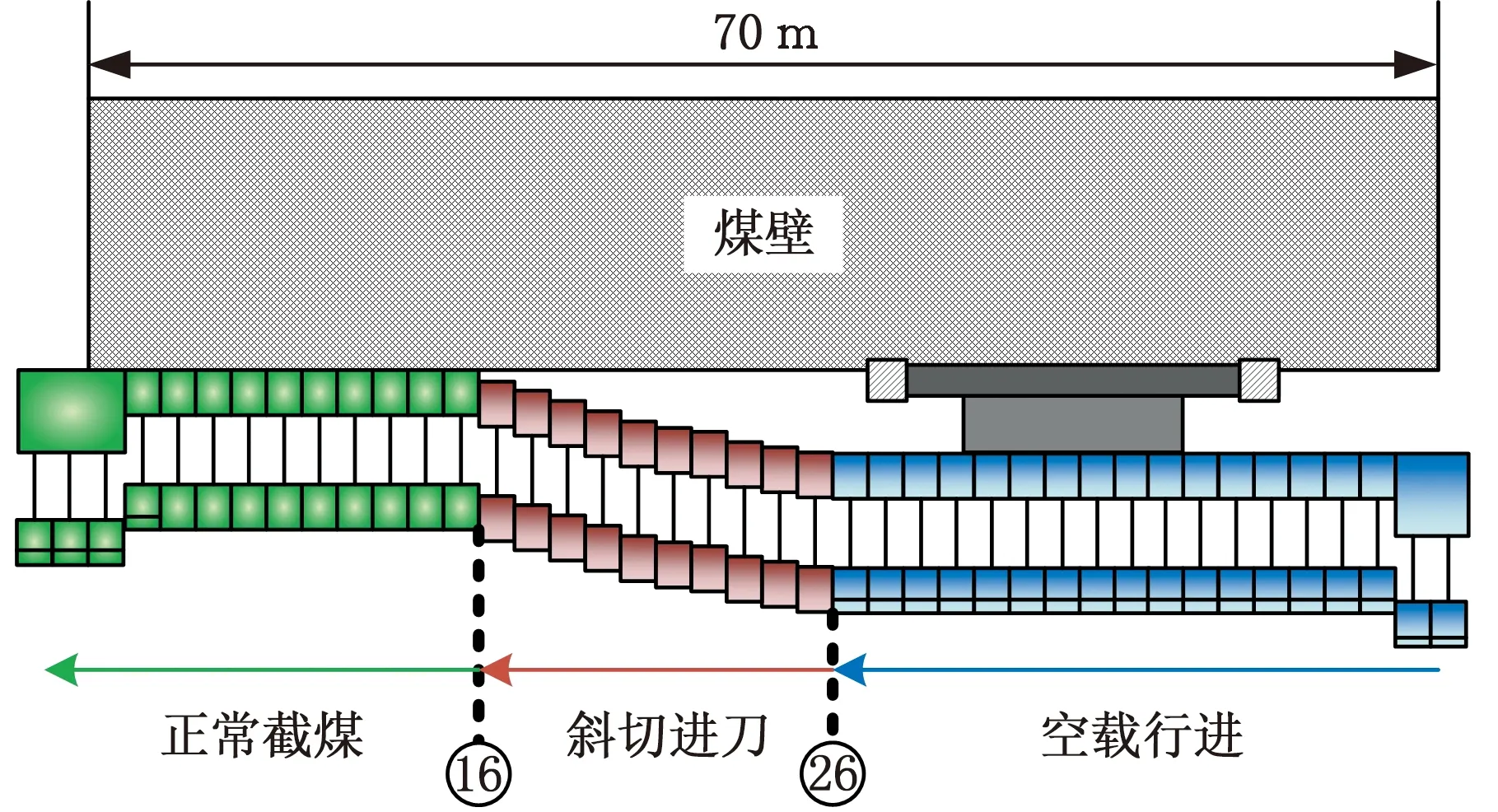
图7 实验测试三机状态Fig.7 Status of 3 experimental machines

数据处理后，由样本数据中提取的100个测试实验数据点所构成的连接架销轴输入样本曲线(8组)、惰轮轴输入样本曲线(2组)、摇臂应变输入样本曲线(12组)分别如图8～图10所示。

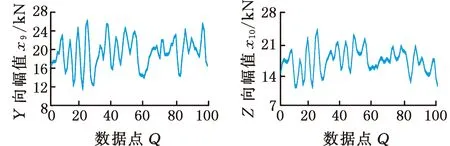
图9 惰轮轴Y向和Z向输入样本Fig.9 Y and Z input samples of idler wheels

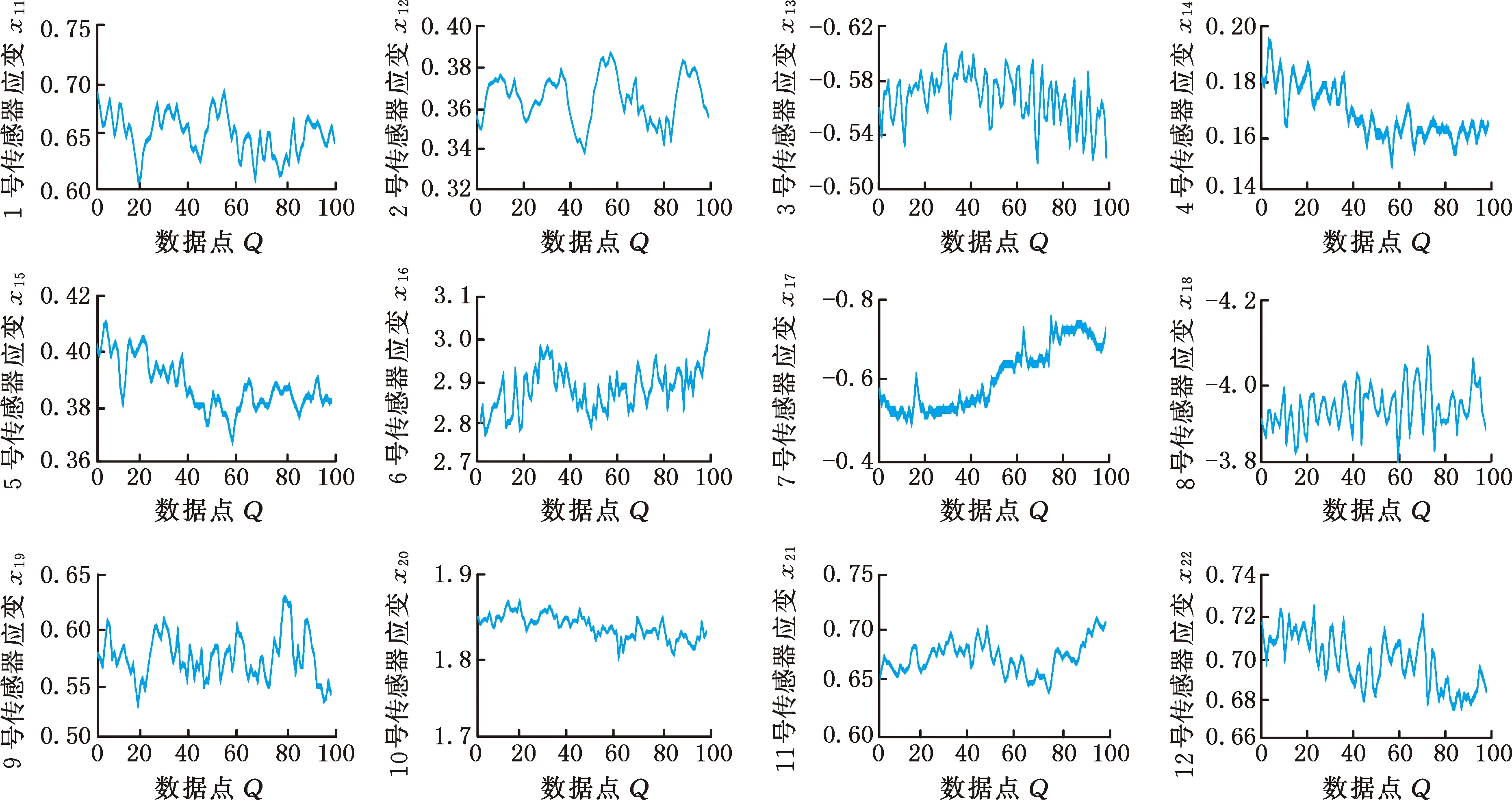
图10 摇臂应变输入样本Fig.10 Rocker strain input sample

5 数据对比分析

首先将测试样本输入到BR-PSO-DBN预测模型中，然后经过数据融合处理，最后输出对应数据点的滚筒三向载荷和滚筒扭矩特征数据。将截齿传感器实际测得的截割载荷数据与采煤机滚筒截割载荷预测模型得到的预测载荷数据进行对比分析，通过载荷预测的精度来验证BR-PSO-DBN模型的准确性。观察图11中滚筒载荷预测值与实测值曲线可知：预测曲线与实测曲线的变化规律较为相似，曲线中峰值点的位置是一一对应的，说明预测结果能够准确地反映滚筒实际载荷变化特征。

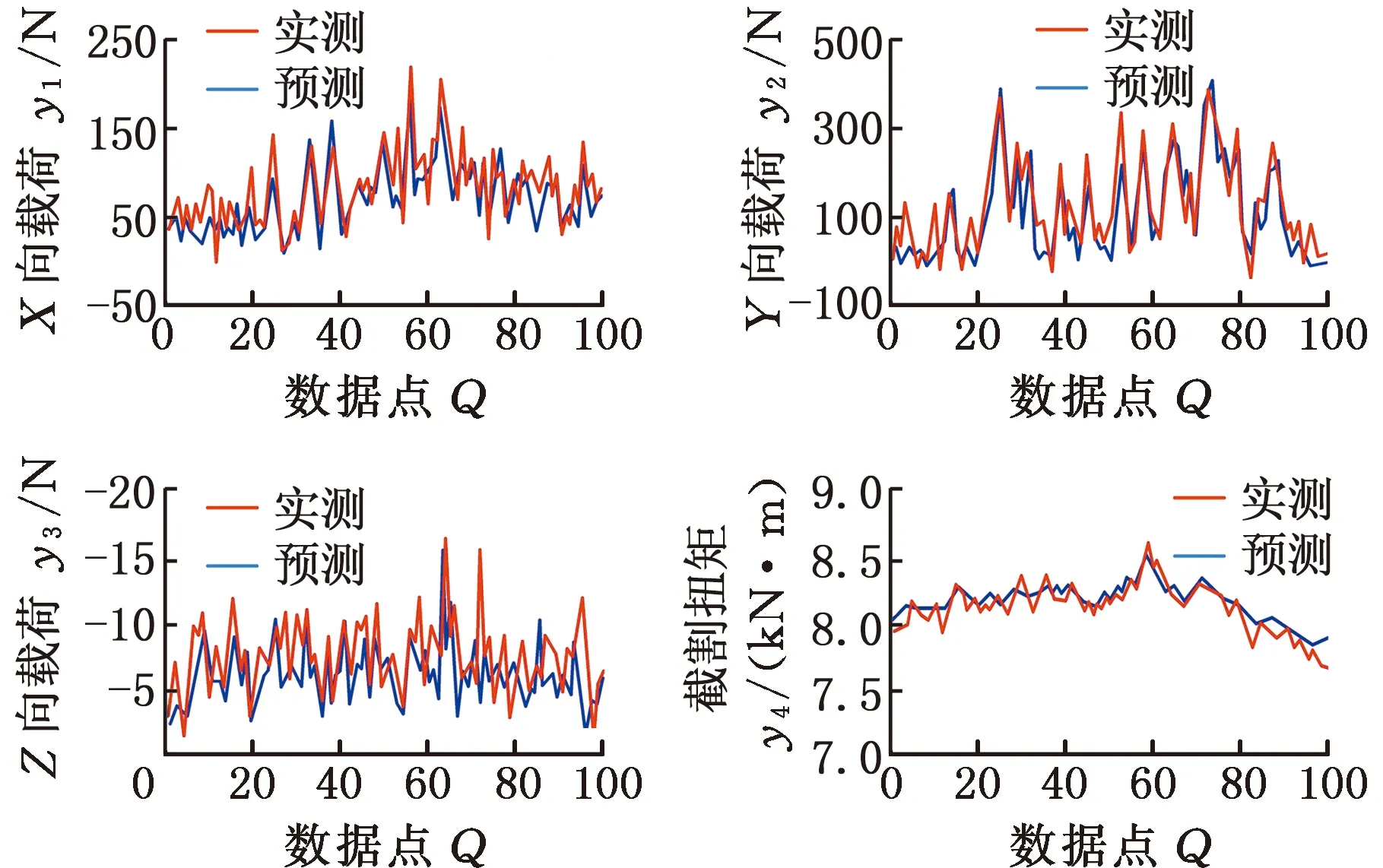
图11 实测曲线与预测曲线对比 Fig.11 Comparison of measured and predicted curves

对实验数据与预测数据作进一步处理，得到预测与实测数据如表1所示，将截割载荷的BR-PSO-DBN预测值和实验值从平均值、最大值、最小值和标准偏差4个方面进行比较：在X向和Y向上的滚筒截割载荷以及滚筒扭矩的预测值略小于实际测试值，在Z向的截割载荷预测值略大于实际测量值。4个载荷测试结果的相关系数分别为0.8370、0.8926、0.8765和0.9455，均在0.83以上，其中滚筒扭矩预测值与实际测试值的近似程度最高，达到了95%，说明BR-PSO-DBN预测模型可以准确地预测滚筒的截割扭矩，在X、Y和Z向上的截割载荷误差相对较大，但预测值与实验值之间的相似度超过83%，证实了该预测值具有较高精度，BR-PSO-DBN模型预测截割载荷的方法具有可行性。

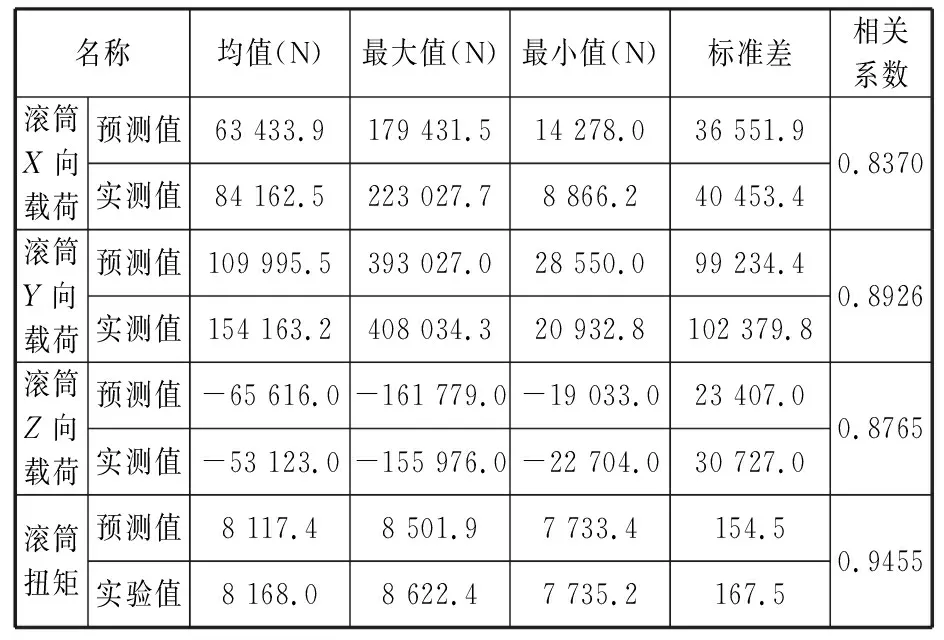
表1 预测与实测数据误差对比分析

6 结论

(1)本文采用BR-PSO-DBN模型从多传感器数据中抽取状态特征信息融合，实现截割载荷的预测与辨识，解决了单一传感器监测效能低和截割载荷预测精度低的问题。

(2)以深度信念网络为框架，在无监督学习和有监督学习阶段分别引入贝叶斯正则化和改进的粒子群算法对传统深度信念网络结构进行优化，建立了BR-PSO-DBN截割载荷预测模型。

(3)通过实验系统测试得到惰轮轴载荷数据、连接架销轴载荷数据、摇臂应变数据，归一化处理后创建训练样本和测试样本，并导入训练样本，获得最优的网络参数，完成了BR-PSO-DBN模型的训练。

(4)输入以22个变量的100组数据组成的测试样本，输出滚筒截割载荷和扭矩的预测数据，将预测曲线与现场实验系统实测曲线进行比对，两组曲线变化趋势基本相同，对应峰值基本一致。

(5)数据处理后，将两种结果的相关系数进行对比。BR-PSO-DBN预测模型对截割载荷预测精度达到了83%以上，其中滚筒扭矩预测精度最高，达到了95%，进一步验证了截割载荷预测具有很高精度，预测方法能够应用到实际生产中对采煤机滚筒载荷进行识别，提高采煤机截割煤岩安全状态感知力。