TNTZ钛合金流变行为及物理基本构模型

钟明君 王克鲁 程 静 欧阳德来 崔 霞 李 鑫

1.南昌航空大学航空制造工程学院，南昌，3300632.南昌航空大学材料科学与工程学院，南昌，330063

0 引言

Ti-29Nb-13Ta-4.5Zr(TNTZ)钛合金作为Ti-Nb-Ta-Zr系中的第三代新型β型医用钛合金，具有低弹性模量、高比强度、良好的耐磨耐蚀性和生物相容性等特点，被广泛用于人工关节、骨骼修复、脊柱固定器等生物医用材料领域，具有极其重要的医用价值[1-3]。

本构模型是描述金属材料在塑性变形过程中流变应力动态响应的数学模型，该模型刻画了流变应力与热变形参数(应变速率、变形温度和应变)之间的非线性函数关系。金属材料在塑性加工时，流变应力的大小既是衡量材料塑性加工能力的重要指标，也是设备选择和模具相关设计的依据和前提[4]。由于钛合金在热加工过程中变形抗力大，对变形温度和应变速率较为敏感，成形比较困难，因此，研究TNTZ钛合金热变形过程中的流变行为和本构模型对合理制定其热加工工艺具有重要意义。

近年来，国内外学者对TNTZ钛合金的各项性能展开了一系列研究。黄海广等[5]采用放电等离子体烧结技术(SPS)制备了综合性能优良的TNTZ钛合金，研究了烧结温度对其致密度、微观组织和力学性能的影响。王冉[6]通过向TNTZ钛合金中添加稀土氧化物Y2O3，研究了Y2O3对TNTZ钛合金腐蚀磨损性能的影响规律，结果表明Y2O3的添加可以改善TNTZ钛合金的力学性能，提高合金的硬度、耐腐蚀性和耐磨损能力。物理基本构模型考虑了材料内部组织结构的变化，将宏观参数(应变速率、变形温度、应变量)与材料相关的物理基础参数(自扩散激活能等)进行结合，在预测流变应力的同时还能有效地反映材料的物理特性。然而，目前对TNTZ钛合金热变形过程中的流变行为和本构模型的研究还十分有限，尚未出现利用物理基本构模型预测TNTZ钛合金流变应力的相关报道。

本文通过对TNTZ钛合金进行等温恒应变速率压缩实验，探究了不同工艺参数对TNTZ钛合金流变应力的影响规律，为优化TNTZ钛合金的热加工工艺参数及有限元数值模拟提供参考。

1 实验材料与方法

本实验所用材料为锻态TNTZ钛合金棒料，其名义成分为Ti-29Nb-13Ta-4.5Zr，该合金的主要化学成分如表1所示。采用机械加工将TNTZ钛合金制备成φ8 mm×12 mm的圆柱状试样，然后在Gleeble-3500热模拟机上对其分别进行变形温度为700，750，800，850，900 ℃，应变速率为0.001，0.01，0.1，1 s-1的等温恒应变速率压缩实验。所有试样的最终高度压下量均为70%，实验以10 ℃/s的速度将试样加热至变形温度后保温300 s，以使温度均匀，热压缩结束后立即喷水冷却至室温。采用线切割机沿试样轴线切割压缩试样，并按标准制备金相试样，采用体积比为V(HF)∶V(HNO3)∶V(H2O)=1∶3∶7的腐蚀液进行腐蚀，最后利用XJP-6A金相显微镜观察其原始微观组织。图1所示为TNTZ钛合金的原始组织。

表1 TNTZ钛合金化学成分(质量分数)

图1 TNTZ钛合金的原始组织Fig.1 Original microstructure of TNTZ titanium alloy

2 结果与分析

2.1 流变行为分析

图2为变形温度为700～900 ℃、应变速率为0.001～1 s-1条件下TNTZ钛合金的流变应力曲线。由图2可知，在同一变形温度下，TNTZ钛合金的流变应力随着应变速率的增大而增大，表明该合金为正应变速率敏感材料。这是由于随着应变速率的增大，材料在相同形变程度下的变形时间大幅缩短，位错增加以及运动使得材料内部位错群堆积，促使材料的临界切应力增大；短时间内材料的动态软化无法利用位错的滑移和攀移充分进行，导致该合金流变应力增大[7-8]。而在同一应变速率下，TNTZ钛合金的流变应力随变形温度的升高而明显减小，表明TNTZ钛合金为负温度敏感材料。这是由于变形温度升高，原子的动能增大，原子间相互结合的能力减小，导致材料的临界切应力减小；同时，温度的升高促进了热激活作用，动态软化效应高于加工硬化作用，使得位错密度下降，从而导致该合金流变应力减小[9-10]。一般认为流变曲线中的动态软化与变形热效应密切相关。

(a)t=850 ℃

2.2 变形热的计算

材料在压缩过程中，大部分塑性功转化为热能，导致试样温度升高，称为变形热效应。实际上，在等温压缩过程中，虽然试样表面的温度保持不变，但由于热量不能迅速耗散，致使试样内部的局部温度有不同程度的升高。当温度和变形应变相同时，变形热对流变应力的影响主要取决于应变速率，因此，变形热效应不可忽视。由变形热效应产生的温升可表示为[11]

(1)

(2)

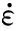
图3 TNTZ钛合金在不同应变速率下的温升曲线Fig.3 Temperature rise curves of TNTZ titanium alloyat different strain rates

利用TNTZ钛合金热压缩实验所获得的流变应力曲线数据，根据式(1)和式(2)计算不同变形条件下的温升值。图3为TNTZ钛合金在不同应变速率下的温升曲线，可以看出，当变形温度一定时，变形热效应引起的温升与应变速率正相关，即随着应变速率的增大而增大。特别是在低温高应变速率下尤为明显，当变形温度为700 ℃，应变速率为0.001 s-1和1 s-1时，变形热的最大值分别达到33.881 ℃、85.716 ℃，相差约2.5倍。这主要是因为在低应变速率条件下，合金试样产生的变形热大部分能够通过夹具散失到外界环境中，对变形试样的温度影响不大；而在高应变速率条件下，合金试样的变形抗力增大，变形时间较短，单位时间内的变形量增大，在短时间内无法将产生的变形热及时散失而大量存储于试样内部，从而导致试样温度急剧上升[12]。当应变速率一定时，变形热的大小与温度成负相关，即随变形温度的升高而减小。这主要是因为变形温度越高，合金试样与外界环境中的温差越大，热量散失速度加快，热压缩产生的变形热可以迅速散失；此外，高温变形时合金变形抗力减小，单位体积变形所需能量也随之减少[13-14]。

2.3 物理基本构模型

与传统Arrhenius型双曲正弦本构模型相比，物理基本构模型考虑了变形温度对材料自扩散系数和弹性模量的影响，不仅可以表征材料的流变行为，还可以揭示材料的物理特性[15]，其表达式为[16-17]

(3)

(4)

(5)

式中，B、α为材料常数；n为蠕变指数；D(T)、E(T)分别为材料自扩散系数和弹性模量与温度之间的关系函数；D0为扩散常数；Qsd为自扩散激活能，J/mol；R为气体常数，R=8.314 J/(mol·K)；E0、G0分别为材料在温度为300 K时的弹性模量和剪切模量，MPa;Tm为材料的熔点，K。

式(3)～ 式(5)中TNTZ钛合金相关材料参数可参照表2[18-20]。

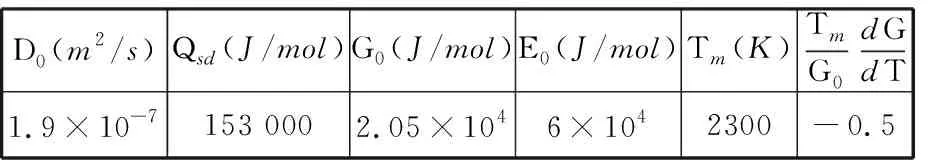
表2 TNTZ钛合金的相关材料参数[18-20]

为了获得式(3)中的三个未知材料参数(α、n、B)，引入以下方程[21-22]：

(6)

(7)

式中，B1、B2、n1、β为材料常数；α=β/n1。

将式(6)和式(7)两边取对数整理得到：

(8)

(9)

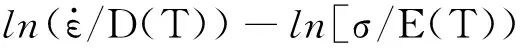
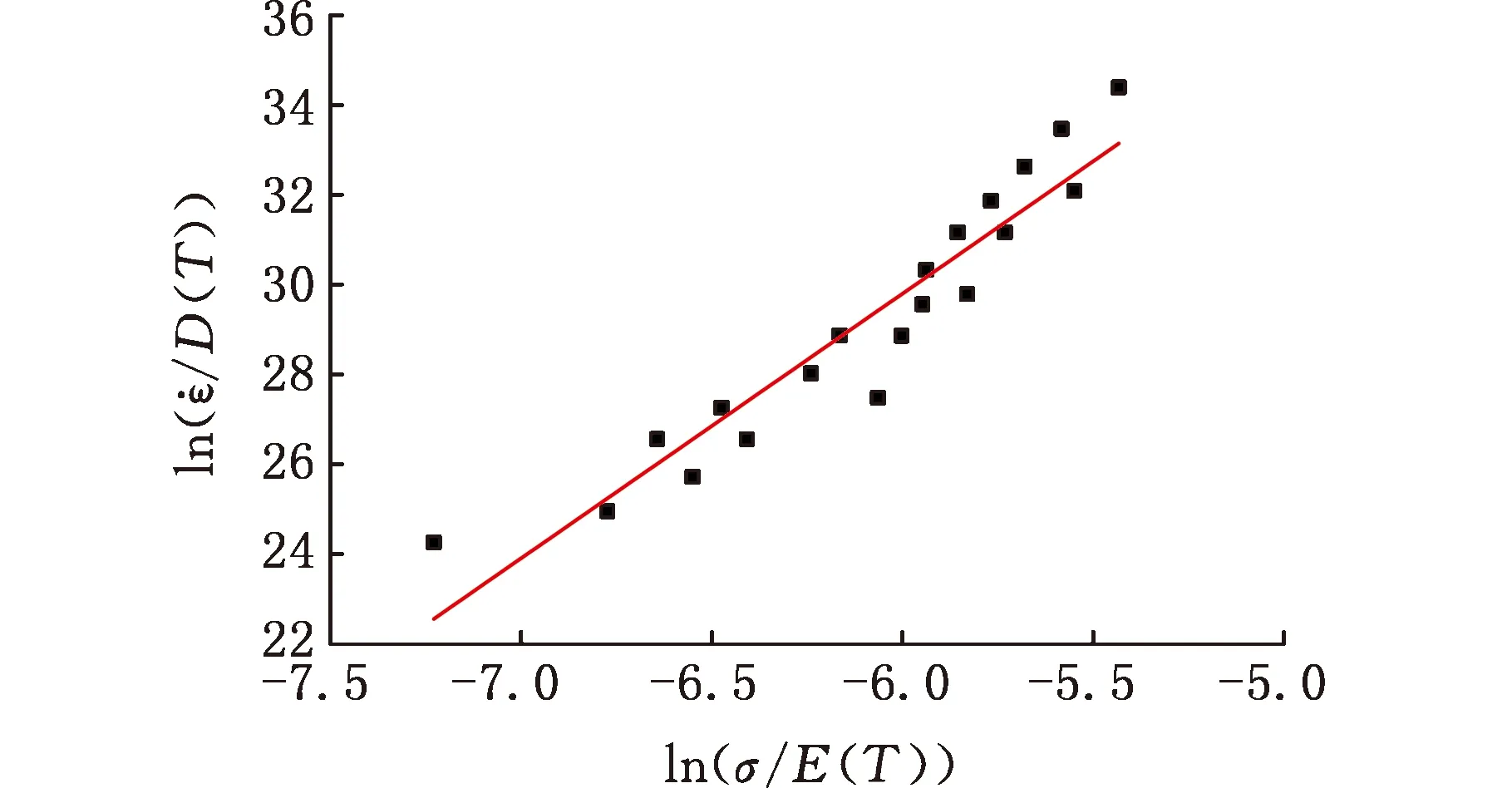
图4 真应变为0.6时的拟合曲线Fig.4 Fitting curves with true strain of 0.6

将以上所求的材料参数代入式(3)，可得TNTZ钛合金在真应变为0.6时的物理基本构模型：

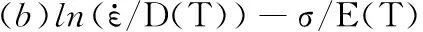
(10)

2.4 基于应变补偿的物理基本构模型

根据上述求解过程，同理可计算不同应变下的材料参数α、n、lnB，结果如表3所示。由于物理基本构模型是基于材料在塑性变形中的稳态流动建立的，故本构模型的求解没有考虑应变对流变应力的影响。要建立更为精确的本构模型，应变累积对流变应力的影响不容忽视。通过多元线性回归拟合材料参数(α、n、lnB)与应变之间的函数关系，研究不同变形程度下本构模型中材料参数随应变的变化规律，发现9次多项式拟合精度最好，拟合曲线见图5。由多项式拟合确定的函数表达式为

(11)

表3 不同应变下的材料参数Tab.3 Material parameters at different strains

将式(11)嵌入到式(3)中进行变换，得到TNTZ钛合金在变形温度为700～900 ℃、应变速率为0.001～1 s-1条件下基于应变补偿的物理基本构模型：

(12)

(a)α

2.5 基于应变补偿的物理基本构模型的验证

为了验证建立的基于应变补偿的物理基本构模型的准确性，将应变0.1～1.2依次代入式(11)，从而求得与应变相对应的材料参数α、n、lnB，再将相关的温度、应变速率和应变分别代入到基于应变补偿的本构方程式(12)，求得相应变形条件下的流变应力预测值，最后与流变应力的实验值进行比较，从而确定基于应变补偿的物理基本构模型对TNTZ钛合金在变形温度为700～900 ℃、变形速率为0.001～1 s-1条件下的适用性。图6所示为应变补偿本构模型的流变应力预测值与实验值对比，可以看出，通过应变补偿建立的物理基本构模型，其预测值和实验值吻合良好。

此外，采用相关系数R和平均相对误差EAR对所建立的本构模型精度进行进一步评价，其表达式如下:

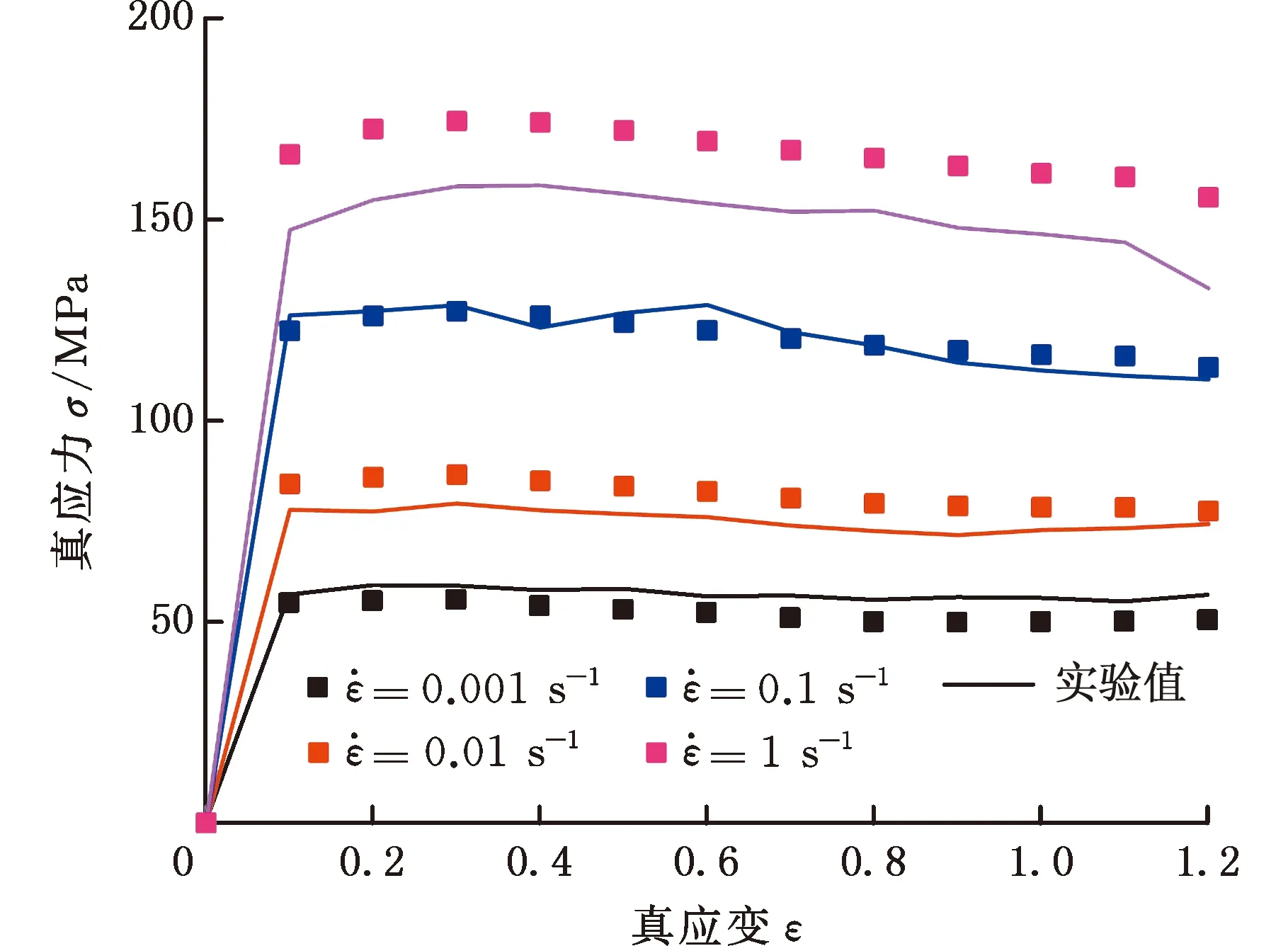
(a)t=850 ℃

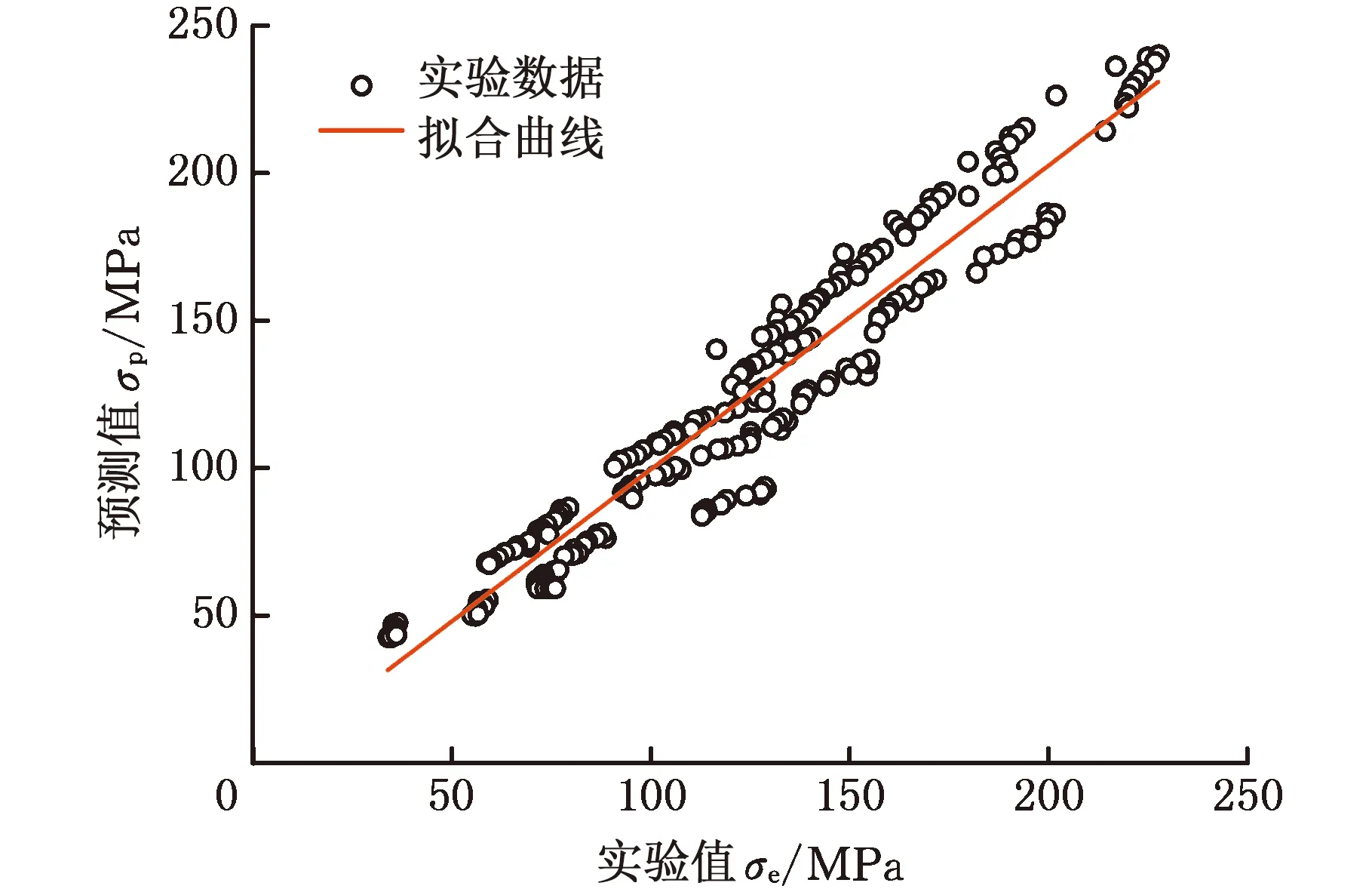
图7 TNTZ钛合金流变应力实验值与应变补偿物理基本构模型预测值的对比Fig.7 Comparison between experimental values ofrheological stress for TNTZ titanium alloy and predictedvalues of strain compensation physically basedconstitutive model

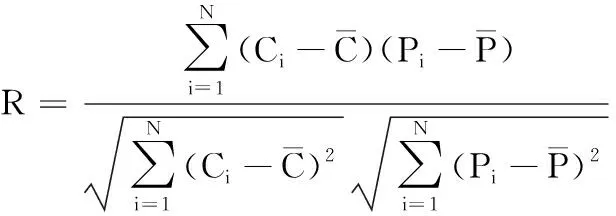
(13)

(14)

式中，N为数据点；C为实验值；P为预测值。

将整理的预测值与实验值代入式(13)和式(14)计算R与EAR，结果如图7所示。经计算，基于应变补偿的物理基本构模型流变应力预测值与实验值的相关系数R达到0.964，平均相对误差EAR为10.63%，进一步证明所建立的基于应变补偿的物理基本构模型具有较高的预测精度。

3 结论

(1)TNTZ钛合金是正应变速率敏感和负温度敏感材料，其流变应力随应变速率的增大而增大，随变形温度的升高而减小。

(2)变形热效应引起的温升大小与应变速率正相关，与变形温度负相关。

(3)通过应变补偿建立的物理基本构模型预测精度较高，流变应力预测值和实验值吻合良好，模型相关系数R为0.964，平均相对误差为10.63%。