负载不平衡下小样本数据的轴承故障诊断

何 强 唐向红，，3 李传江 陆见光，，3 陈家兑

1.贵州大学现代制造技术教育部重点实验室，贵阳，5500252.贵州大学机械工程学院，贵阳，5500253.贵州大学公共大数据国家重点实验室，贵阳，550025

0 引言

在工业生产中，机械传动设备的安全运行是工业生产过程中的核心要求，设备故障可能会导致严重的经济损失乃至灾难性事故。轴承作为机械传动装置必不可少的零件，有必要对其进行监测与诊断。

轴承恶劣的工作环境(如负载不平衡、变负载、变转速)对轴承可靠性诊断提出了挑战。负载不平衡在轴承旋转时会产生一个与转速同频的不平衡激励力，从而引起轴承的不平衡振动，因此从负载不平衡轴承上测得的振动信号具有非平稳性特点[1]，很难从中提取到有效特征用于故障诊断。短时傅里叶变换(short-time Fourier transform，STFT)作为时频分析方法的一种，能够有效处理非平稳信号，目前在机械故障诊断中已得到了广泛的应用。HE等[2]利用LAMSTAR神经网络对经过STFT预处理的传感器信号进行分类，实现了各种工况下轴承故障精确诊断；王丽华等[3]提出了一种基于短时傅里叶变换和卷积神经网络(CNN)的故障诊断方法，成功应用于异步电动机的故障诊断。由于轴承工作环境以及数据采集设备等原因，实际上采集到的轴承工作数据是有限的；同时，由于轴承大多数时候都处于正常运行状态，导致了其故障样本更为稀少。上述方法虽然实现了机械设备故障的精确诊断，但是训练数据对基于深度学习的故障诊断方法有着较大影响，在小样本、数据不平衡等情况下，其诊断性能会严重下降[4-5]。

2014年，GOODFELLOW等[6]提出了生成对抗网络(generative adversarial network，GAN)，它在图像生成方面具有显著的能力。针对机械设备故障故障样本量少、数据不平衡等问题，生成对抗网络被引入故障诊断领域。文献[4]提出了一种结合GAN和堆叠自动编码器(stacked denoising auto encoder，SDAE)的齿轮箱故障诊断方法，它在小样本情况下依然具有较好的诊断效果；文献[7]提出一种基于GAN的往复式机械故障诊断方法，它在数据极端失衡情况下依然有效；文献[8]提出了一种小样本条件下基于GAN的旋转机械故障诊断方法。以上方法虽然在故障样本生成方面具有一定的贡献，但依然缺乏以下两点考虑：其一，大多数基于GAN的故障诊断方法单单针对时域信号或频域信号，不能良好地利用振动信号的频域信息与时域信息；其二，GAN及其变种都是建立在图像处理领域上的，基于一维信号的GAN故障诊断方法不能充分发挥出其图像生成能力。

本文将STFT与梯度惩罚Wasserstein距离生成对抗网络(WGAN-GP)相结合，通过STFT构建轴承振动信号的时频谱图，在充分利用振动信号时域信息与频域信息的同时，更好地发挥WGAN-GP的图像生成能力。此外，构建自注意力卷积神经网络(SeCNN)以进一步提高模型对不平衡负载的抗干扰能力。分析CUT-2实验平台两种负载不平衡轴承数据集，实验结果表明该方法具有良好的鲁棒性和泛化能力，且在小样本条件下具有较好的故障诊断性能。

1 STFT变换、GAN网络以及自注意力模块

1.1 短时傅里叶变换

STFT变换是一种针对突变、非平稳信号的时频分析方法，通过STFT能够将一维的振动信号转变为包含时域、频域信息的二维矩阵。它的基本思想是：为时域信号加上具有固定长度的滑动窗，并对窗内的信号做傅里叶变换，得到窗长度这一时间段内的局部频谱，随着窗口在信号上的平移，最终可以得到每一时间段上频谱的集合。STFT的一般数学表达式为

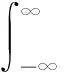
(1)

式中，g(t-τ)为τ时刻的滑动窗；f(t)为时域信号。

1.2 生成对抗网络

GAN网络主要由生成器G与鉴别器D两个模块组成。生成器主要职能是接收已知分布的随机噪声z，并尽力输出与真实样本分布一致的假样本G(z)；鉴别器主要职能是接受混合有真实样本与假样本的数据集，并尽力从中辨别出真实样本与假样本。生成器与鉴别器通过不断地博弈学习来提高各自拟合真实样本的能力与鉴别真假样本的能力。生成器与鉴别器在交替训练中达到纳什均衡，其一般数学表达式为

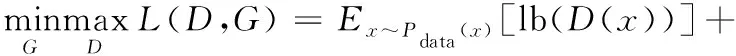
(2)

式中，D(·)、G(·)分别为生成器与鉴别器的输出值；x～Pdata(x)表示输入样本x的分布为Pdata(x)；z～Pz(z)表示输入噪声z的分布为Pz(z)；E[·]为期望函数。

由于JS散度导致了GAN训练不稳定、模式崩塌等问题，故Wasserstein距离生成对抗网络(Wasserstein generative adversarial network，WGAN)[9]引入了一种新的分布度量距离，即Wasserstein Distance，也叫做EM距离，定义为

(3)

式中，Ⅱ(p,q)表示分布p、q的联合分布；(x,y)采样自联合分布r；Ε(x,y)～y[‖x-y‖]为距离‖x-y‖的期望；inf{·}表示集合的下确界；W(p,q)为分布p、q的Wasserstein距离。

WGAN从理论层面上分析了GAN训练不稳定的原因，并有效解决了问题。然而，WGAN权重裁剪的实现方式存在两个问题：其一，网络的权重大部分都集中在两端，这使得神经网络的学习变成了简单的函数映射；其二，对网络权重的强制裁剪容易造成梯度消失或梯度爆炸。为解决以上问题，WGAN-GP[10]被提了出来，采用增加梯度惩罚项的方式来迫使判别器满足1-Lipschitz函数约束。同时，将梯度值约束在1周围时网络的效果会更好，梯度惩罚项的定义为

(4)

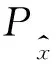
相对于WGAN，WGAN-GP收敛速度更快，生成样本质量更好。

1.3 自注意力模块

自注意力机制已成功应用于语音识别[11]、图像处理[12-13]等领域。本文将自注意力机制引入轴承故障诊断以进一步提高故障诊断效率。自注意力机制的实现参考文献[14]中的SE(Squeeze-and-Excitation)模块。由于本文自注意力模块是在网络的全连接层后实现的，因此不需要额外的全局平均池化操作(Squeeze)。此外，在Excitation操作中多加入一层全连接层以进一步加强自注意力机制对故障特征的非线性拟合能力。自注意力模块实现如图1所示。

图1 自注意力模块示意图Fig.1 Schematic diagram of self-attention module

自注意力模块一共有FC1、FC2、FC3三个全连接层，两个ReLU激活函数和一个 Sigmoid激活函数。首先，第一个全连接层将特征维度降到输入特征维度(X-dim)的1/16，第二个全连接层将特征维度增加到X/4，再分别使用ReLU激活函数；第三个全连接层将特征维度恢复到X，也就是输入特征维度。通过这样的设计可以提高自注意力模块对振动信号中复杂故障特征的非线性拟合能力。此外采用全连接层以及ReLU激活函数这样的结构可使参数量、计算量极小。然后使用Sigmoid激活函数对第三个全连接层的输出进行激活，这样就得到了区间[0,1]的权重值。最后将权重值与输入特征的元素按位相乘就实现了自注意力模块。

2 基于WGAN-GP和SeCNN的轴承故障诊断方法

针对轴承振动信号易受负载不平衡干扰、故障样本数量少等问题，提出基于WGAN-GP和SeCNN的故障诊断方法。诊断过程如下：首先对轴承振动信号进行短时傅里叶变换，得到信号的时频谱图，分为训练集、验证集、测试集；然后将训练集输入到WGAN-GP中进行对抗训练，直至网络收敛，从生成器中生成与训练样本分布相似的新样本，将新样本添加到训练集中以扩充训练集；最后，将扩充后的训练集输入到SeCNN中进行训练，并将训练好的模型应用于测试集，输出故障识别结果。诊断流程见图2。

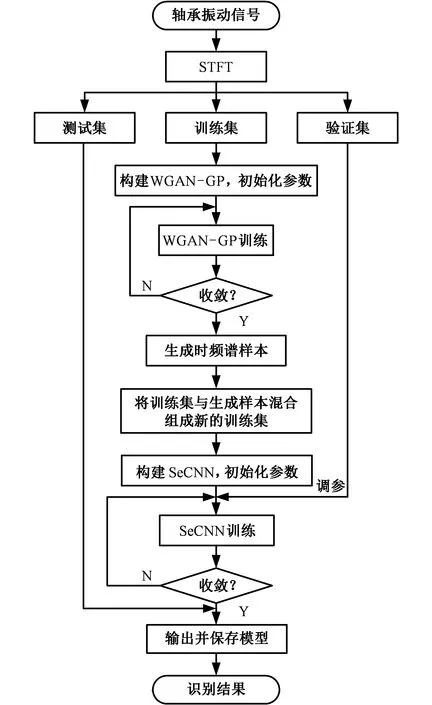
图2 基于WGAN-GP和SeCNN的轴承故障诊断流程图Fig.2 Flow chart of bearing fault diagnosis basedon WGAN-GP and SeCNN

2.1 使用WGAN-GP生成时频谱样本

实际工业中收集足够的轴承故障数据是比较困难的，因此将少数样本的时频谱作为WGAN-GP的真实样本，训练WGAN-GP并生成与真实样本分布相似的时频谱样本。基于WGAN-GP模型生成的高质量时频谱样本能够进一步丰富原始数据集、提高诊断模型的鲁棒性，从而有助于实现轴承故障的精确诊断。WGAN-GP模型结构示意图见图3。

图3 WGAN-GP示意图Fig.3 Schematic diagram of WGAN-GP

生成器的输入为随机噪声z，它采样自区间为[-1,1]上的均匀分布；生成器的输出为合成样本G(z)，其分布与真实样本X分布相似。鉴别器的输入为真实样本X或合成样本G(z)，输出为线性函数值y。因为卷积运算在特征提取上的能力已被证明，所以本文模型WGAN-GP的鉴别器和生成器主要由卷积与转置卷积构成。生成器与鉴别器网络详细结构图见图4。

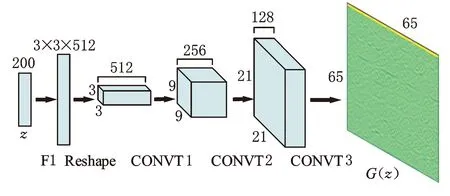
(a)生成器

在生成器G中，输入为符合均匀分布的随机噪声z，噪声维度为200。该输入先经过全连接层F1扩维，然后将数据重组为三维张量并使用LeakyReLU[15]激活函数，最后通过三层转置卷积操作生成大小为(65,65,1)的张量，也就是生成的时频谱样本，其中前两层转置卷积均采用批量归一化。第一层转置卷积的卷积核个数为256，大小为3，步长为3，LeakyReLU作为激活函数；第二层转置卷积的卷积核个数为128，大小为5，步长为2，LeakyReLU作为激活函数；第三层转置卷积的卷积核个数为1，大小为5，步长为3，使用Tanh激活函数。

在鉴别器D中，一共3个卷积层，卷积核大小均为4，步长均为2，卷积核个数分别为64、128、256，均将LeakyReLU作为激活函数；最后一层为全连接层，节点个数为1，不使用激活函数。

在训练WGAN-GP时可以用鉴别器的loss值来指示模型训练进度，鉴别器的loss值越趋向于收敛就代表模型训练得越好，生成的样本质量越高。鉴别器的loss值定义如下：

(5)

在WGAN-GP训练中，基于上述损失函数，迭代更新模型参数。采用Adam[16]优化器，鉴别器学习率为0.0001，生成器学习率为0.0002，两者交替训练直至鉴别器loss值收敛。

2.2 基于自注意力机制的卷积神经网络

本文提出的基于自注意力机制的卷积神经网络(SeCNN)旨在减小不平衡负载对数据的影响、提高模型的轴承故障特征提取能力，进而实现轴承故障抗干扰诊断。SeCNN的输入为混合了真实时频谱样本和生成时频谱样本的训练集，通过验证集识别准确率指示SeCNN模型的训练进度，最后将训练好的SeCNN模型用于测试集识别，并输出识别结果。本文提出的SeCNN模型主要由最大池化层、卷积层以及自注意力模块组成，SeCNN结构图见图5。

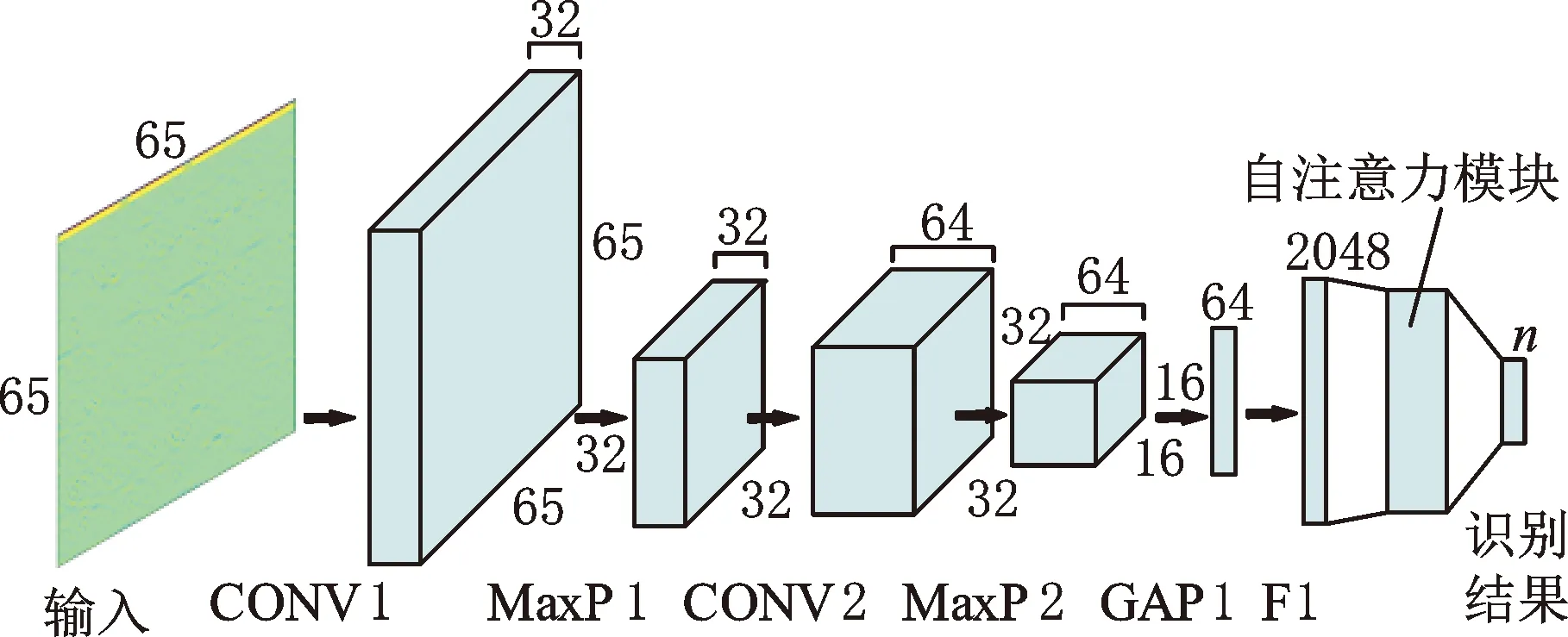
图5 SeCNN模型结构图Fig.5 SeCNN model structure diagram

在SeCNN中，卷积层CONV1和CONV2的卷积核大小均为3，步长均为1，卷积核个数分别为32、64，使用ReLU激活函数；池化层MaxP1和MaxP2的窗口大小均为2，步长均为2；GAP1为全局平均池化层；F1为全连接层，节点数为2048；输出层节点数为输入样本的类别数n，采用Softmax激活函数。

3 实验与结果分析

为了验证本文所提方法的有效性，针对轴承实测的振动信号，分析该方法在轴承负载不平衡和小样本情况下的鲁棒性和泛化能力。

3.1 数据集描述

轴承实验数据来源于CUT-2轴承实验平台，平台如图6所示。实验轴承型号为6900ZZ，使用电火花加工技术分别在轴承外圈、滚珠、内圈加工直径为0.2 mm和0.3 mm的故障，单点故障以及复合故障如图7所示。使用加速度传感器采集轴承振动信号，采样频率10 kHz，轴承转速3000 r/min。轴承不平衡负载的构建分为两种：第一种为加装负载在负载盘上单点连续分布；第二种为加装负载在负载盘上半盘均匀分布。每种轴承负载不平衡条件下采集12类故障，包含单点故障以及复合故障。每类故障采集200个样本，样本长度为1024，按照2∶1∶1把数据集分为训练集、验证集和测试集，具体的数据集信息如表1所示。同时设定短时傅里叶变换的窗函数长度为128，窗函数重叠点数为112，每个样本对应生成的时频谱图尺寸为65×65。

图6 CUT-2轴承实验平台Fig.6 CUT-2 bearing test platform

(a)外圈故障 (b)内圈故障 (c)球体故障 (d)复合故障图7 轴承故障的位置Fig.7 Location of the bearing faults

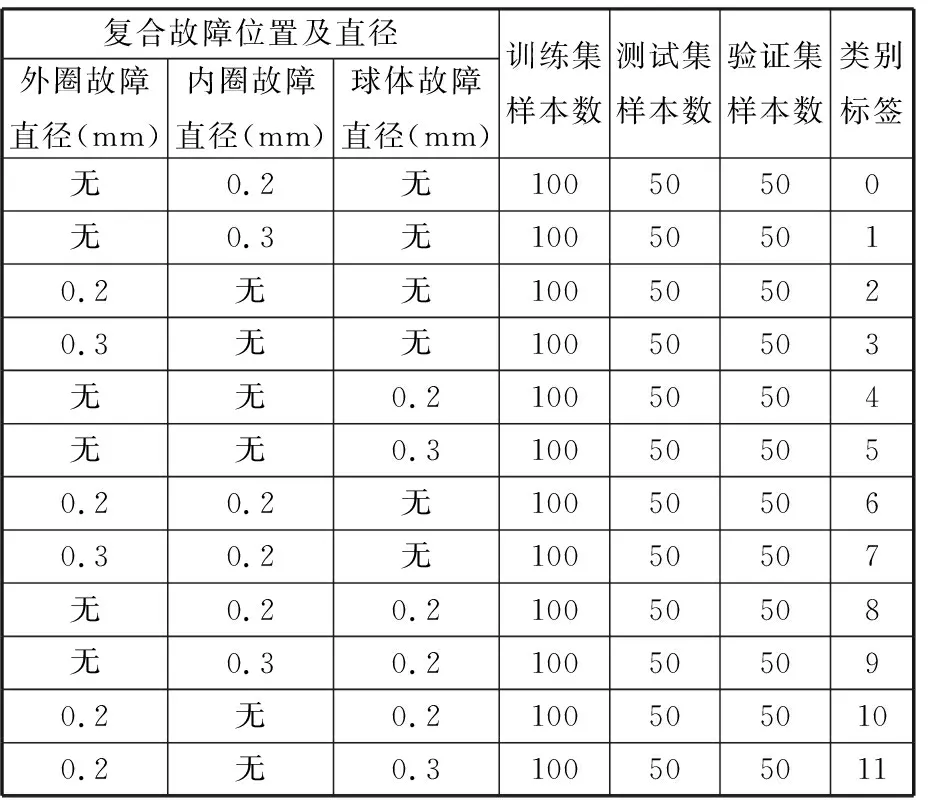
表1 CUT-2平台轴承数据集

3.2 WGAN-GP模型训练及数据生成

使用第一种负载不平衡轴承数据训练集对所提出的WGAN-GP模型进行训练。训练轮数设为2000，模型批处理样本数目为10，每类故障生成的时频谱样本数量预设定100，训练集做区间为[-1,1]的归一化处理。基于深度学习框架Tensorflow进行模型的搭建与训练，记录鉴别器loss的值并获得合成样本，实验结果如图8所示。

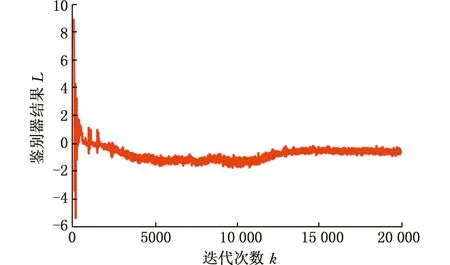
图8 鉴别器loss变化曲线Fig.8 Loss variation curve of discriminator

由图8可以看出，最初鉴别器loss值由大幅振荡迅速趋向于收敛但随后又出现小幅振荡，说明此时模型正处于学习阶段，并没有找到最优解方向。经过15 000次迭代后，鉴别器loss值小幅波动并趋向于平稳，说明此时WGAN-GP已经得到了很好的训练，生成器合成的时频谱样本分布已经很接近故障样本分布。待模型训练完毕后，从生成器获得合成的时频谱样本。表2展示了传感器获取的故障标签为1～6的真实样本及其时频谱图和对应生成器合成的时频谱样本。由表2可以看出，合成的时频谱图与真实时频谱图很相似但又不完全相同，这说明模型既有效学习到故障特征，又保证了合成样本的高质量、多样性。

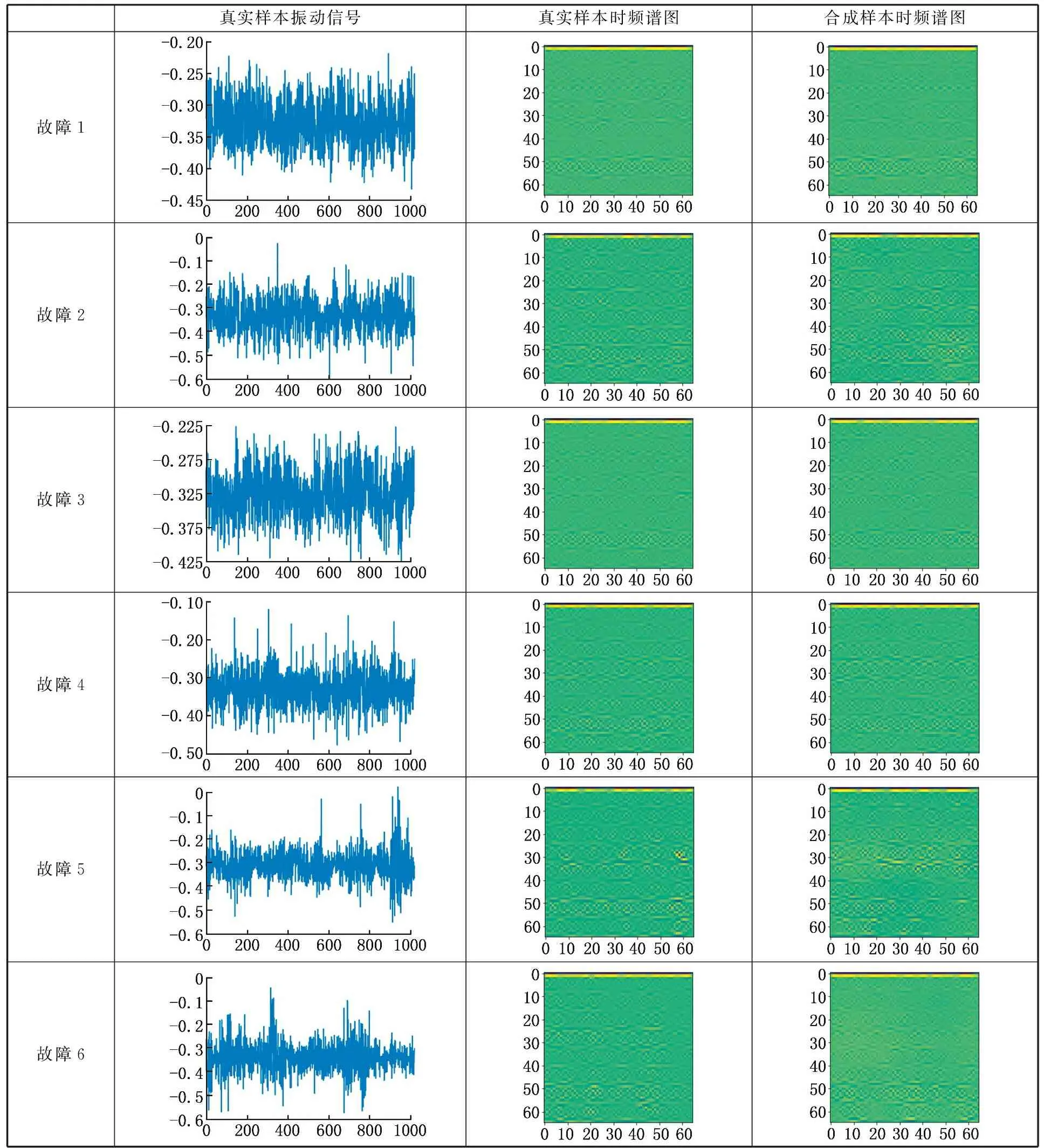
表2 真实样本及其时频谱图与合成样本时频谱图

3.3 SeCNN模型训练及合成样本质量评估

SeCNN采用Adam优化器更新模型参数，学习率设置为0.001，训练轮数设置为100，批处理样本数目为10。虽然训练轮数设置为100，但是本文在SeCNN的训练过程中引入了Early-Stopping机制，在一定训练轮数内，如果模型的验证集的准确率没有提高，则停止训练并保存模型参数。训练集准确率及验证集准确率变化曲线见图9。由图9可以看出，模型在第59轮时就达到了停止条件，训练集准确率与验证集准确率趋向于重合，这说明模型被训练良好，且没有出现过拟合现象。

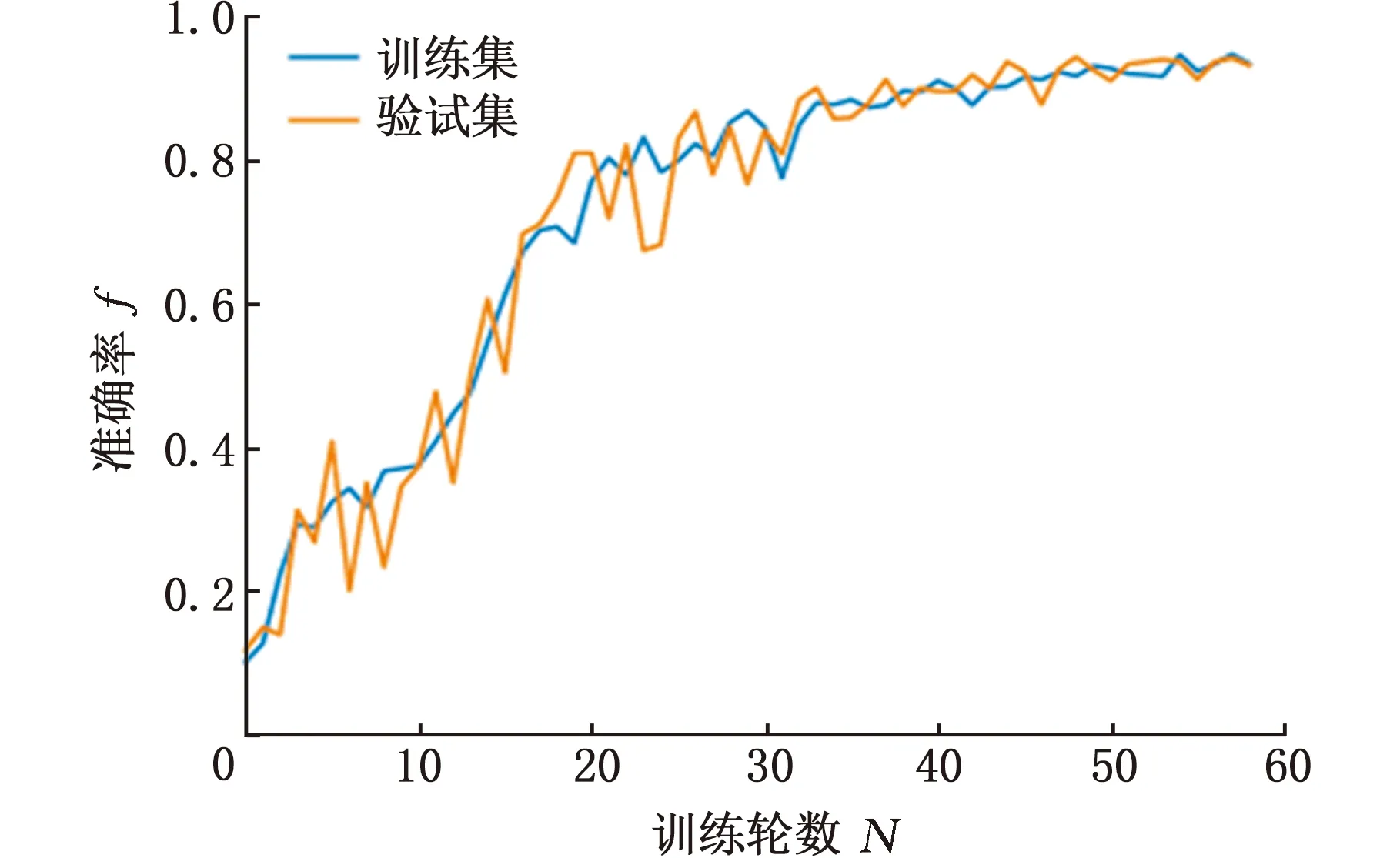
图9 训练集及验证集准确率变化曲线Fig.9 Accuracy change curve of training set andverification set

为了进一步评估合成样本的质量以及合成样本数量对SeCNN模型学习的影响，每类故障分别生成100、200、500、1000个样本，将生成的样本与初始训练集混合组成新的训练集输入到SeCNN中，并将训练好的SeCNN模型应用于测试集。为了避免实验结果受随机因素的影响，每次测试均进行10次重复性实验，计算出模型的平均准确率及其标准差，实验结果如表3所示。表3中，实验方法SeCNN表示没有向训练集中添加合成样本，SeCNN_100、SeCNN_200、SeCNN_500、SeCNN_1000表示向训练集每类故障分别添加100、200、500、1000个合成样本。

由表3可以看出,当向训练集每类故障添加合成样本的数量达到500个时，SeCNN平均准确率达到了94.23%，相较于没有添加合成样本的SeCNN来说其平均准确率提高了3.01%，准确率标准差更是减小了82%，充分说明了通过WGAN-GP合成样本的高质量、多样性以及对故障诊断模型性能的有效提高。值得一提的是，SeCNN_1000相较于SeCNN_500，平均准确率虽然只提高了0.19%，但是其准确率标准差却减小了81.13%，这说明了大数据对基于深度学习的故障诊断模型的泛化能力以及稳定性具有显著提高作用。

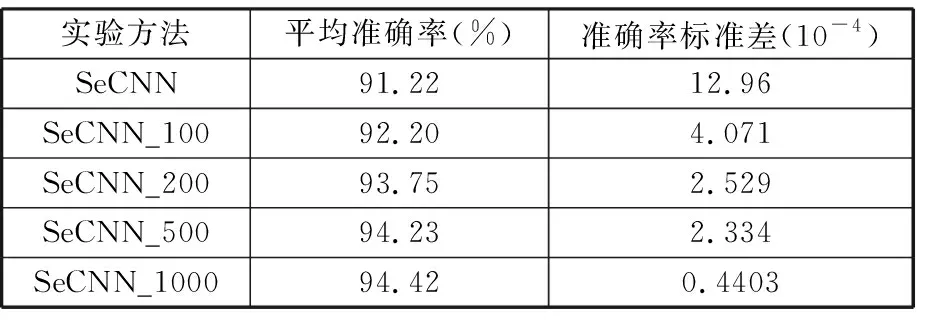
表3 生成不同样本的数量对模型SeCNN的影响

3.4 与其他深度学习方法的对比实验

为了进一步验证本文基于短时傅里叶变换的WGAN-GP+SeCNN轴承故障诊断方法的有效性，将其与CNN以及文献[3]、文献[17]、文献[18]中算法共四种算法进行对比。其中CNN是不带自注意力模块的SeCNN，输入为时频谱图，其他参数与SeCNN保持一致。每种算法进行10次重复性实验，实验结果如表4所示。

表4 第一种轴承负载不平衡下不同算法实验结果

由表4可以看出，文献[17]与文献[18]提出的基于一维振动信号的故障诊断算法对负载不平衡下的轴承数据集诊断精度较低，不能有效识别出各种故障。其中文献[17]的诊断精度只有10.27%，这可能是由于其卷积核设置过大，不能有效学习到故障局部特征所致；通过查看其训练过程发现训练集准确率已经达到100%，但是验证集却只有10%左右，说明该模型已经出现了严重的过拟合现象。文献[18]虽然诊断精度相对于文献[17]有所提高，但是该算法是基于一维时域信号的故障诊断方法，丢失了信号的频域信息；其次，批处理大小设置为64，在样本量较小时不能发挥出算法的性能，所以文献[18]的诊断精度依然较低。文献[3]与算法CNN+STFT都是基于短时傅里叶变换的故障诊断方法，其诊断精度相较于基于一维振动信号的故障诊断方法有了很大提高，这说明短时傅里叶变换能很好地应对非平稳信号，且时频域信息的样本在提高数据量的同时对模型性能也有较大提高。此外，由表4算法SeCNN的实验结果可以看出，相对于没有自注意力机制的CNN+STFT以及文献[3]来说，其诊断精度有了一定提高，这说明自注意力模块在抑制噪声权重、提高故障特征权重方面具有比较明显的作用。本文方法相较于其他主流故障诊断方法具有较大优势，相较于文献[3]与算法CNN+STFT的故障诊断方法其准确率提高了4%以上，准确率标准差减少了95%以上，验证了本文方法在轴承负载不平衡下基于小样本数据的故障诊断具有可行性。

为了说明本文方法在处理轴承负载不平衡问题时的优越性，将负载平衡轴承数据输入到不同故障诊断算法中进行训练与测试，实验结果如表5所示。

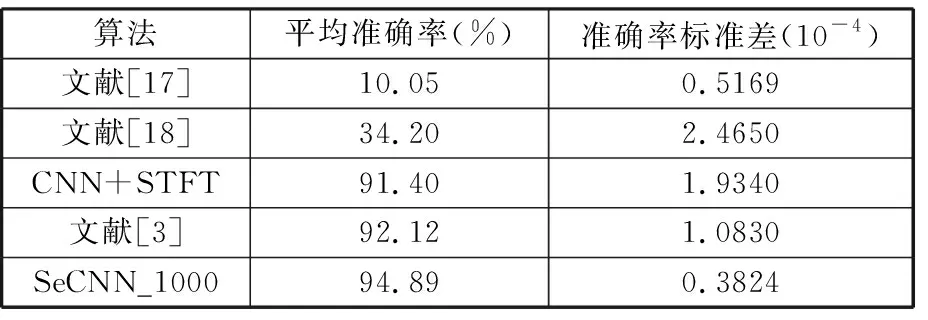
表5 轴承负载平衡下不同算法实验结果

由表5可以看出，文献[17]的平均识别率几乎没有变化，说明该算法没有学习到故障特征，造成了模型的随机分类，这与前文的分析一致。文献[18]的平均准确率在移除负载不平衡的影响后反而下降了，说明影响该算法的主要因素是数据量，较小的样本量造成了模型的不稳定。算法CNN+STFT与文献[3]在负载平衡下不仅平均准确率得到了提高并且准确率标准差也减小了86%左右，这说明在移除负载不平衡的影响后普通算法的诊断性能与稳定性都得到了提高。对照表4与表5可以看出，本文方法在负载平衡下与负载不平衡下的诊断性能相近，这说明该方法对负载不平衡具有较好的鲁棒性。

3.5 鲁棒性与泛化性能实验

为了进一步验证轴承负载不平衡下本文方法的鲁棒性与泛化能力，对第二种负载不平衡轴承数据集进行实验与分析。使用轴承训练集对WGAN-GP进行训练，通过实验发现，当训练轮数达到5000时，模型鉴别器的loss值处于收敛状态，因此确定训练轮数为5000。将本文方法与其他四种故障诊断方法进行对比，所有配置与前文保持一致，每种模型进行10次重复实验，实验结果如表6所示。

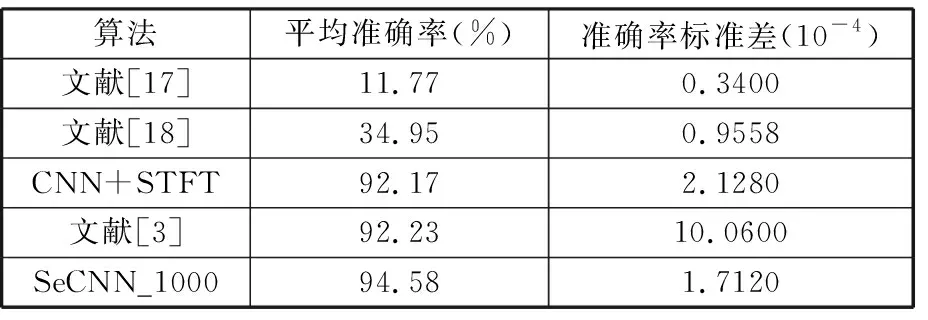
表6 第二种轴承负载不平衡下不同算法实验结果

由表6可以看出，本文方法相较于其他四种算法具有明显优势，故障识别平均准确率达到了94.58%，能够有效分辨出轴承负载不平衡下的复合故障与单点故障，证明了该方法具有良好的鲁棒性与泛化性能。

4 结论

(1)将振动信号通过短时傅里叶变换转为时频谱能够充分利用的时域与频域信息，并且时频谱样本方便生成对抗网络(GAN)处理，可更好地发挥其生成图像的优势。

(2)利用梯度惩罚Wasserstein距离生成对抗网络(WGAN-GP)生成时频谱样本，丰富了数据集，可以有效提高基于深度学习的故障诊断模型的泛化能力和鲁棒性。

(3)基于自注意力机制的卷积神经网络在面对负载不平衡条件下的轴承时，其故障诊断能力相较于普通卷积神经网络有了较大提高，说明将自注意力机制引入到故障诊断领域中具有可行性。