阵列天线DOA跟踪环路鉴别器性能分析

关刚强，李柏渝，聂俊伟，王飞雪

（国防科学技术大学电子科学与工程学院，湖南　长沙 410073）

阵列天线DOA跟踪环路鉴别器性能分析

关刚强，李柏渝，聂俊伟，王飞雪

（国防科学技术大学电子科学与工程学院，湖南长沙 410073）

网址：www.sys-ele.com

利用阵列天线波束指向空间相关性的特点，可以构建一个类似于传统锁相环结构的闭合环路以实现对导航信号来波方向（direction of arrival，DOA）的跟踪。DOA跟踪环路中鉴别器的实现方法主要有实部相减相干法、幅值相减归一化法、功率相减归一化法，首先基于波束形成技术建立了阵列天线导航接收机DOA跟踪模型，在此基础上从鉴别器增益、收敛范围和输出噪声方差3个方面对比分析了采用不同角度鉴别器算法的跟踪性能，最后对其进行了仿真验证。

阵列天线；波束形成；来波方向跟踪；鉴别器

0　引　言

在利用阵列天线导航接收机对载体平台姿态测量的工程应用中，平台姿态的改变将引起载体坐标系下信号来波方向（direction of arrival，DOA）矢量的变化，因此姿态实时测量过程中对载体坐标系下导航信号DOA的连续估计问题即是对信号DOA的跟踪问题［1 2］。具有超分辨能力的空间谱估计算法如多重信号分类算法［3］、旋转不变子空间算法等均需要对接收数据协方差矩阵进行特征值分解［4］，具有较高的计算复杂度，而且信号DOA快速变化时可能引起空间谱的扩展，将严重降低DOA的估计性能，通常不能满足载体平台姿态实时测量的需求。

针对基于阵列天线的信号DOA跟踪问题，已有国内外文献对此进行了相关的研究，如文献［5-8］利用投影近似子空间跟踪算法递归估计信号子空间能够解决空间谱扩展问题并避免了特征值的分解，但需要额外的搜索过程才能获得信号的DOA估计。文献［9-13］提出了利用角度跟踪环路算法来跟踪信号DOA并对其进行了研究，但其仅考虑了相干法和非相干功率法的角度鉴别器，其分析有一定的局限性，本文在此基础上对DOA跟踪环路中常用的不同实现算法下的鉴别器性能进行了分析对比和仿真验证。

1　基于波束形成的DOA跟踪模型

如图1所示，基于波束形成技术的阵列天线导航接收机DOA跟踪利用阵列波束指向的空间相关性特点在阵列波束宽度内生成两个关于当前时刻信号DOA的估计值对称的观测波束，通过对两个观测波束接收的数据进行处理从而获得当前时刻信号DOA误差信息，并更新信号DOA估计值，从而形成一个闭合的跟踪回路。

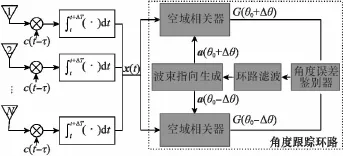
图1　基于波束形成技术的导航接收机DOA跟踪框图

由于导航信号伪码良好的互相关特性，仅考虑单颗卫星信号时经过相关积分解扩处理后的阵列天线接收数据矢量可写为

式中，α、φ为导航信号的幅度和相位残留；d（k）为导航电文符号；θ、a（θ）分别为该颗卫星信号的DOA和对应的导向矢量；v（t）为均值为零方差为σ2I的高斯白噪声，I为单位矩阵。设第k个观测时刻的信号DOA估计为，利用两个对称的观测波束对阵列接收数据进行空域相关，则空域相关器的输出可分别表示为

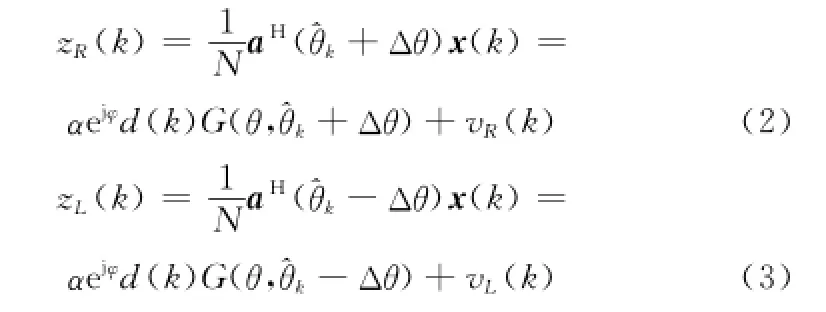
式中，N为阵列天线阵元个数；（·）H为共轭转置运算；Δθ为角度间距，即两观测矢量夹角的一半；a（θ1）为归一化空域相关函数；υ为两个观测波束的噪声分量。角度误差鉴别器根据空域相关函数的特点通过对两个观测波束的输出进行处理从而获得当前时刻的信号DOA估计误差信息，可表示为

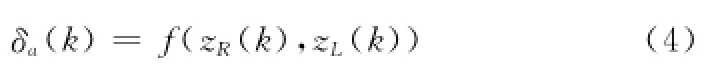
式中，f（·）为鉴别器函数。将角度误差经过环路滤波后获得下一时刻的DOA估计并更新观测波束指向。第（k+1）时刻的DOA估计值为

式中，K0为环路增益；h（k）为环路滤波器的冲击响应函数；⊗表示卷积运算。若当前时刻的DOA估计值小于真实信号DOA值θ，则角度误差鉴别器的输出δa（k）将大于0，下一时刻更新后的DOA估计值将增大；反之，则下一时刻更新后的DOA估计值将减小。从而使阵列天线导航接收机的观测波束指向随着导航信号DOA改变的方向移动，通过迭代直至DOA估计收敛于真实的信号DOA。

2　DOA跟踪环路鉴别器对比分析

2.1鉴别器实现算法对比

DOA跟踪环路中常用的鉴别器实现算法如表1所示，根据获取角度误差的处理方式不同，主要分为相干鉴别器和非相干鉴别器，非相干鉴别器包括幅值相减归一化法和功率相减归一化法。

表1　DOA跟踪环路鉴别器实现算法对比

实部相减相干法需要剥离导航信号的载波相位残留和电文符号调制，而且其鉴别结果还受信号振幅的影响；幅值相减归一化法鉴别器中空域相关器输出幅值需要经过求根才能获得，而功率相减归一化法则避免了求根运算，因此后者相对于前者计算量有所减少［14］，然而由于空域相关器输出的幅值曲线与功率曲线不相重合，二者的收敛特性也存在差异，考虑到鉴别器的作用是让DOA跟踪环路朝着使两个对称的观测波束接收到的信号功率相等的方向上调节，这两种鉴别器算法最终也会使DOA跟踪环路收敛。

2.2鉴别器增益和收敛区间定义

鉴别器收敛区间为使DOA跟踪环路能够收敛的初始角度误差范围，当初始的角度误差超过收敛区间时，环路可能假锁到其他伪收敛点上［15］。如图2所示，定义收敛区间Iθ为鉴别器输出曲线上第一个极大值点与第一个极小值点之间的角度范围。由于收敛区间内各点的斜率不同，考虑到环路稳定跟踪时误差一般都较小，因此将鉴别器增益定义为鉴别器曲线DOA估计误差为零处的斜率ks，可近似计算为

式中，fθ为DOA估计误差为θ的鉴别器输出。

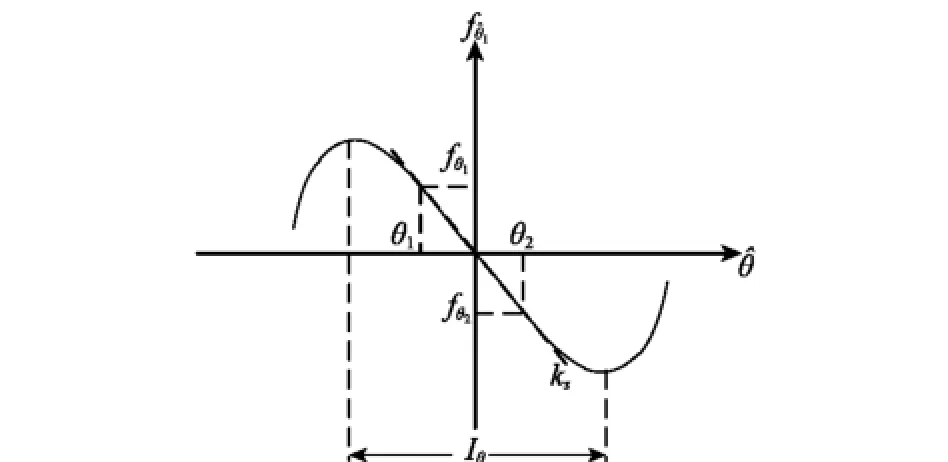
图2　鉴别器增益和收敛范围定义

2.3鉴别器输出方差分析

当跟踪环路处于稳态时，角度误差鉴别器可近似为线性函数，此时鉴别器输出可写为

式中，υε（k）为噪声部分。将式（7）代入式（6）则DOA跟踪误差的迭代过程可重写为

对式（9）进行z变换，则有

式中，υε（z）为鉴别器输出噪声分量υε（k）的z变换；H（z）为环路滤波器在z平面的传递函数。一般情况下K0ks≫1，此时DOA跟踪环路的均方误差为

式中，BL为系统函数F（z）的双边等效噪声带宽。若系统函数一定，则角度误差鉴别器的输出方差将直接影响到信号DOA跟踪的误差方差。

首先考虑采用实部相减相干算法时，鉴别器输出的噪声部分为其方差为

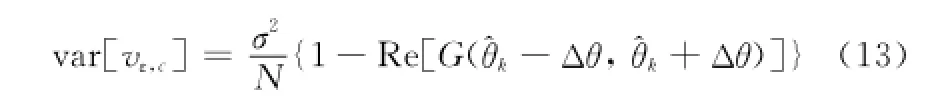
当采用非相干角度鉴别器算法时，由于对输出进行了归一化处理，很难获得解析形式的噪声分量表示，另外考虑到幅值法和功率法的鉴别器性能相近，为分析过程的简便，仅对归一化前的功率相减法鉴别器进行分析，此时其输出噪声部分可写为

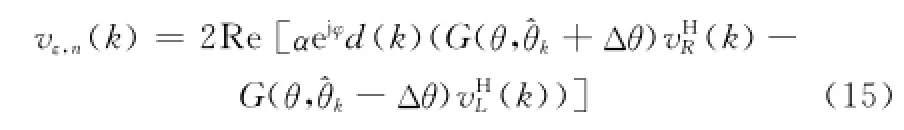
在稳态条件下其方差为

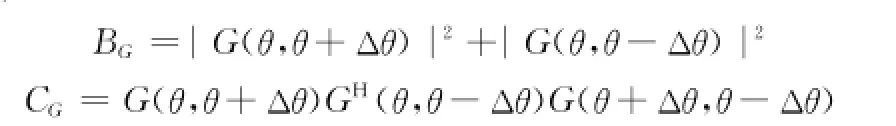
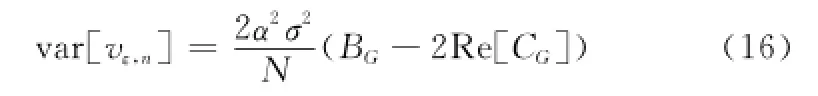
式中

对比式（14）和式（16）可以发现，鉴别器输出方差与阵元个数成N反比，与解扩后的单阵元噪声功率σ2成正比，由于功率法引入的平方损耗，空域相关函数对非相干鉴别器的影响更为明显。

3　仿真验证

以N=12个全向阵元间距为半波长构成的均匀直线阵列为例，假设入射到阵列的导航信号DOA初始值为0°，并以恒定的角速度运动，另设仿真过程中导航信号已成功实现了解调解扩处理。为表述方便，将实部相减相干法、幅值相减归一化法和功率相减归一化法鉴别器分别编号为鉴别器1、2和3，角度间距Δθ=2°时3种不同鉴别器算法的理想鉴别曲线如图3所示。从图3中可以看出，3个鉴别器在各自的收敛范围内均可正常工作，而且鉴别器输出在角度估计误差比较小时呈良好的线性关系。

图3-3种鉴别器的输出曲线

不同实现算法下的鉴别器增益和收敛范围与角度间距的关系分别如图4和图5所示。

图4-3种角度鉴别器的增益

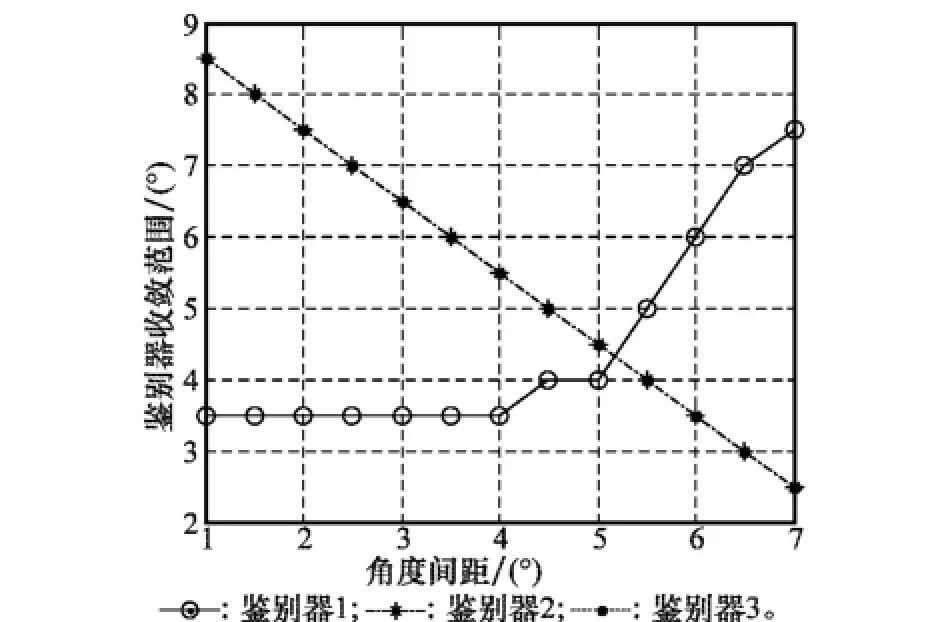
图5-3种角度鉴别器的收敛范围

将σ2/N进行归一化处理，则高斯白噪声环境下采用相干实部求差法和为归一化的非相干功率法的DOA鉴别器输出方差与角度间距的关系如图6所示。

图6　相干和非相干角度鉴别器输出的方差

4　结　论

通过上面的对比分析和仿真结果，可以看出，相干和非相干鉴别器均能实现对导航信号DOA的跟踪，当角度间距在阵列天线波束宽度范围内时相干鉴别器的和增益和跟踪误差方差性能优于非相干鉴别器，而非相干鉴别器的收敛范围则要比相干算法更宽，因此可在DOA跟踪环路的引入阶段利用非相干鉴别器以提高适应性，而在环路锁定后则利用相干鉴别器以提高DOA的跟踪精度。

［1］Chun Y，David M L.Angles of arrival tracking of GPSsignals with digital beamforming monopulse for attitude determination［C］//Proc. of the 60th Annual Meeting of the Institute of Naυigation，2004：521-532.

［2］Chun Y.Digital beamforming monopulse for GPS attitude determination［C］//Proc.of the 14th International Technical Meeting of the Satellite Diυision of the Institute of Naυigation，2001：2037-2047.

［3］Wang Y L，Chen H，Peng Y N，et al.Spatial spectrum estimation theory and algorithm［M］.Beijing：Tsinghua University Press，2004：2-13.（王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京：清华大学出版社，2004：2-13.）

［4］Chen Q，Lei H，So H C.Computationally efficient ESPRIT algorithm for direction-of-arrival estimation based onNystrom method［J］.Signal Processing，2014，94：74-80.

［5］Javier S A，Sylvie M.An efficient PASTd-algorithm implementation for multiple direction of arrival tracking［J］.IEEE Trans. on Signal Processing，1999，47（8）：2321-2324.

［6］Liu C N，Wang GM，Xin J M，et al.Low complexity subspace based two dimensional direction-of-arrivals tracking of multiple targets［C］//Proc.of the 11th International Conference on Signal Processing，2012：1825-1829.

［7］Xenofon G D，George VM.Fast and stable subspace tracking［J］. IEEE Trans.on Signal Processing，2008，56（4）：1452-1465.

［8］Mu Z，Alle J V.Stable subspace tracking algorithm based on a signed URV decomposition［J］.IEEE Trans.on Signal Processing，2012，60（6）：3036-3051.

［9］Seunghyun M，Dongyoun S，Kwang B L，et al.Direction-of-arrival tracking scheme for DS/CDMA system：direction lock loop［J］. IEEE Journal on Wireless Communications，2004，3（1）：191-202.

［10］Wang A D.Tracking the spatial multiple targets based on array signal processing［D］.Hangzhou：Zhejiang University，2010.（王安定.基于阵列信号处理的空间多目标跟踪［D］.杭州：浙江大学，2010.）

［11］Sebt M，Sheikhi A，Nayebi M.Robust low-angle estimation by an array radar［J］.IET Radar，Sonar&Naυigation，2010，4（6）：780-790.

［12］Dongmin P，Eunjung Y，Soyeon A，et al.Adaptive beamforming for low-angle target tracking undermultipath interference［J］. IEEE Trans.on Aerospace and Electronic Systems，2014，50（4）：2564-2577.

［13］Evgeny M.Method of automatic target angle tracking by sumand-difference monopulse radar invariant against the polarization jamming［C］//Proc.of the 7th European Radar Conference，2010：499-502.

［14］Xie G.Principlesof GPS and receiυer design［M］.Beijing：Publishing House of Electronics Industry，2009：307-317.（谢钢.GPS原理与接收机设计［M］.北京：电子工业出版社，2009：307-317.）

［15］Tang X M.Weak signal receiving technology for high-performance GNSS receiver based on precise model［D］.Changsha：National University of Defense Technology，2010.（唐小妹.基于精确模型的高性能卫星导航弱信号导航接收技术研究［D］.长沙：国防科学技术大学，2010.）

Performance analysis of discriminators in DOA tracking loop with antenna array

GUAN Gang-qiang，LI Bai-yu，NIE Jun-wei，WANG Fei-xue
（College of Electronic Science and Engineering，National Uniυersity of Defense Technology，Changsha 410073，China）

By using the spatial correlation characteristics of the beam steering vector with antenna array，as similar to the traditional phase lock loop（PLL）a closed loop can be constructed to realize the direction of arrival（DOA）tracking for global navigation satellite system（GNSS）signals by using beamforming.The three most popular implementations of discriminators in the DOA tracking loop are named as the coherent method with real part subtraction，normalization methods with amplitude subtraction and power subtraction.Firstly，a DOA tracking model in the GNSS receiver with antenna array is established by using beamforming，and then the performances of the DOA discriminator are analyzed from three different aspects which are gain，convergence range and noise variance，finally simulation verifications are carried out.

antenna array；beamforming；direction of arrival（DOA）tracking；discriminator

1001-506X（2016）05-0990-04

TN 911

A

10.3969/j.issn.1001-506X.2016.05.03

2015-06-17；

2015-09-18；网络优先出版日期：2015-10-14。

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20151014.0956.004.html

国家自然科学基金（61403413）资助课题

关刚强（1986-），男，博士研究生，主要研究方向为阵列天线导航接收机关键技术。

E-mail：closetoqiang@163.com

李柏渝（1982-），男，讲师，博士，主要研究方向为导航接收机天线射频关键技术。

E-mail：libaiyu@nudt.edu.cn

聂俊伟（1983-），男，讲师，博士，主要研究方向为阵列天线抗干扰技术。

E-mail：niejunwei@nudt.edu.cn

王飞雪（1971-），男，教授，博士，主要研究方向为卫星导航接收机导航定位技术与工程应用。

E-mail：feixuewang_nnc@163.com