超短基线声传感器安装偏差标定测线规划

李　　　昭，郑　翠　娥，孙　大　军

（1.哈尔滨工程大学水声工程学院，黑龙江　哈尔滨 150001；

2.水声技术国防重点实验室，黑龙江　哈尔滨 150001）

超短基线声传感器安装偏差标定测线规划

李昭1，2，郑翠娥1，2，孙大军1，2

（1.哈尔滨工程大学水声工程学院，黑龙江哈尔滨 150001；

2.水声技术国防重点实验室，黑龙江哈尔滨 150001）

利用测线对称性对固定测量偏差的抵消作用，对超短基线声传感器安装偏差标定测线进行了规划。通过分析各类测角偏差对标定的影响，得出安装偏角估值无偏时测线应满足的对称性与重合性条件，规划了满足该条件3类测线：直线测线、圆测线及将两者合并的组合测线，并通过仿真计算与实验数据处理对3类测线进行了比对。仿真与实验结果表明组合测线在不能严格保证对称重合测量的实际情况下标定结果更准确、一致性更好，修正后超短基线系统的定位精度更高。因此将组合测线作为超短基线声传感器安装偏差的标定测线。

超短基线；安装误差标定；测线规划；传感器校准

网址：www.sys-ele.com

0　引　言

超短基线定位系统通过全球卫星定位系统（global satellite positioning system，GPS）、航向/姿态传感器将声学传感器所得的相对位置转换到地理坐标系，以获得被跟踪目标的地理坐标［1-6］。由于航向/姿态传感器和声学传感器通常是分离式安装，从而导致声学传感器坐标系与船只坐标系存在的坐标夹角偏差［1-3］。该偏差是影响系统定位精度的主要因素：1°的艏向安装偏角产生1.7%斜距的定位误差［1-8］。因而在超短基线系统实施定位作业之前须先进行安装偏差标定，通过所采集的标定数据反演声学传感器的安装偏差。而标定数据需要在水面船只沿预定测线围绕水下应答器航行过程中采集［4-6］。通常地，测量计算精度与测量数据采集轨迹几何形状有关［9］，标定数据采集测线同样影响着声传感器安装误差标定准确度，因此标定测线的合理规划能够提高标定作业的有效性。但目前水声定位中涉及测线规划的研究较少，缺乏可借鉴的研究成果：文献［1-3］在论述超短基线标定时指出了一些测量的注意事项，但并未对标定测线进行研究；文献［10］利用模拟退火方法数值反演定位海底基阵阵元所用水面若干测点形成的最优几何图形，但该方法在面对测线中过多未知测点位置的求解时极易发散；IxSea、Sonardyne等公司的超短基线采用了∞形、圆形轨迹标定［11-12］，但未公开其设计考虑因素。国内对超短基线标定研究以圆形标定航迹为主，分析的角度主要从避免声速剖面补偿的角度出发，未考虑观测仪器的偏差对标定性能的影响［6，13］。本文将以减小固定测量偏差对标定影响为出发点，通过理论分析规划测线。

文章首先研究了最小二乘估计在固定测量误差影响下的误差，分析表明利用反向的偏差相消特性可减小估值误差。随后分析了由应答器位置偏差产生的通用横墨卡托格网系统（universal transverse mercartor grid system，UTM）坐标系下测角偏差，以及由声速偏差产生的声学传感器坐标系下测角偏差对各个安装偏角标定的影响，得出无偏估计对应的测量条件。结合该条件与仿真计算结果，规划了由直线和圆组合而成的组合测线作为超短基线声传感器安装偏角的标定测线。仿真计算表明该测线在不能保证对称重合测量的条件时标定精度高、一致性好，并通过湖试验证了该测线的性能。

1　超短基线安装偏角标定原理

超短基线安装偏角指声传感器坐标系与船只坐标系间由安装产生的坐标轴角度偏差，包括：艏向安装偏角、纵倾安装偏角β与横摇安装偏角γ。标定共包含超短基线声传感器坐标系A（简称声传感器坐标系）、船只航向姿态测量系统坐标系S（简称船只坐标系）、UTM大地坐标系U 3个坐标系，3个坐标系的定义参见文献［6］。标定利用在UTM与声传感器两个坐标系下测得的声信号入射方向的偏差估计超短基线安装偏角。标定计算的观测方程［13］为

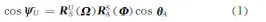
式中，θA=（θAx，θAy，θAz）T为信号入射方向与声传感器坐标系夹角，由超短基线测得；U=（ΨUx，ΨUy，ΨUz）T为信号入射方向与UTM坐标系夹角，由应答器、船只UTM坐标及声速剖面算得。θA、U均为已知量。Φ=（α，β，γ）T为超短基线安装偏角，为待估计量，其定义参见文献［6］。Ω=（H，κ，φ）T代表船只艏向、纵摇与横摇角度，由航向姿态系统测量得到，定义遵循航向姿态测量设备规范。Rlk是坐标系k向坐标系l的变换的变换矩阵，具体形式为

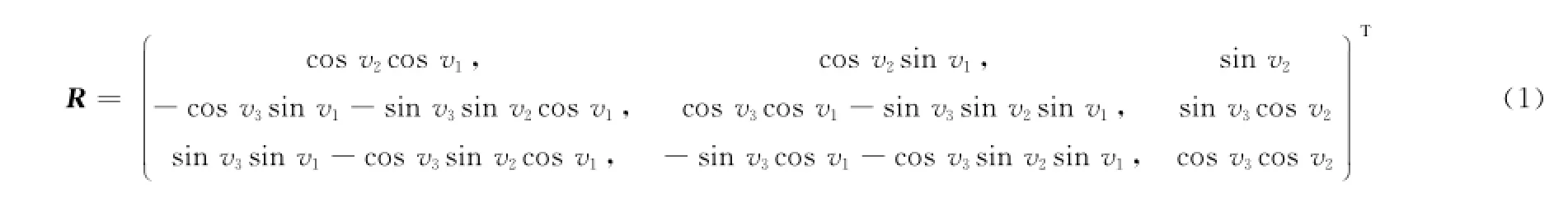
由S坐标系向U坐标系转换时，式中υ1，υ2，υ3代表船只艏向、纵摇与横摇；由A坐标系向S坐标系转换时，则代表待标定的艏向、纵摇与横摇安装偏角。

测量数据中的固定偏差误差会使标定结果有偏。对于超短基线声传感器安装偏角标定而言，测量数据的固定偏差主要包括由应答器位置不准确而使U产生的误差，以及因声速不准确使θA产生的误差［6，13］。

2　固定偏差对最小二乘估值影响

超短基线声传感器安装偏角标定通常基于最小二乘估计（least square method，LSM）原理。现研究当观测数据中存在固定偏差时，LSM估计结果的特性。

令观测模型Pi×j利用无误差数据bi×1估计得到的未知数xj×1为真值，即

则估值x=（PTP）-1PTb。其中，i为观测数据数量，j为未知数个数。假设x1j×1=x+Δx1，x2j×1=x+Δx2为利用两组含不同固定偏差的观测数据b1m×1（i1=m），b2n×1（i2=n）得到的估值结果。若利用全部观测数据估值，则

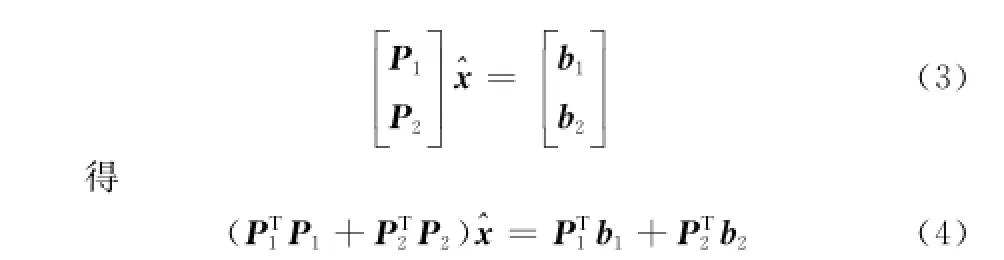
当仅有一组观测数据存在固定误差而导致Δx1=Δx、Δx2=0时，式（4）可写为

以上推导说明：对于相同的观测模型，LSM具有抵消反向的估值偏差、减小估值偏差的特性。若利用可产生反向估值偏差的测点组成超短基线标定测线，则可利用这种抵消特性可提高估计准确度。

3　固定误差对安装偏角标定影响

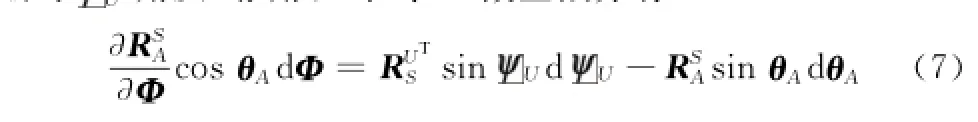
本节将分别分析这两种固定测量误差对安装偏角估计的影响，并寻找能够产生反向估值误差的测点作为规划标定测线的基础。

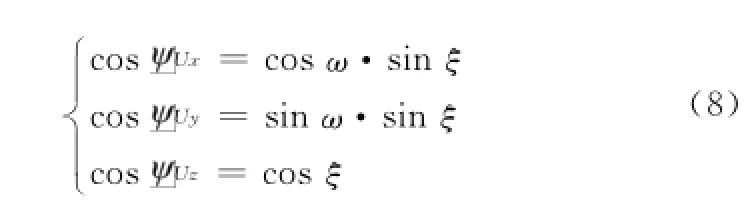
式中，ω为传感器相对应答器的水平方位角

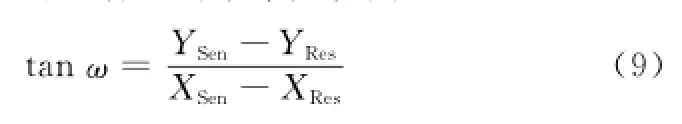
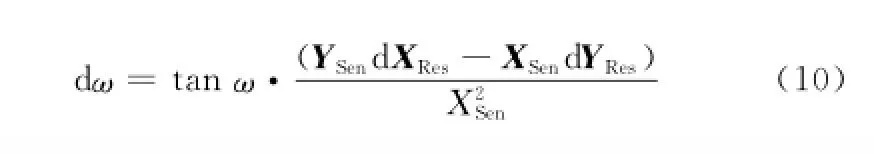
深海条件下（深度大于1 000 m）长基线法定位应答器UTM坐标精度为m级，产生的方位角计算偏差约为0.1°左右，是影响标定精度的主要因素之一。

（XSen，YSen）为传感器UTM坐标，通过船载GPS测量结果转换得到，（XRes，YRes）为应答器UTM坐标，用长基线距离交会法计算得到。ξ为入射声线与水平面法线的夹角，通过声传感器与应答器间的本征声线搜索得到［13］。

将应答器视为坐标中心，当应答器UTM坐标存在偏差时

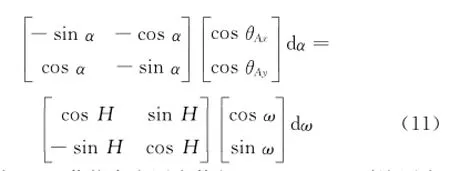
对于式（11），若能存在测点使得dα1=-dα2，则该测点可作为所规划测线的一部分，以抵消固定偏差。

考虑测点关于应答器原点对称：（XSen1，YSen1）= -（XSen2，YSen2），由式（10）易知dω1=-dω2。代入式（11），此时在以下两种条件下满足dα1=-dα2。

条件1θA1=θA2，H1=π+H2，ω1=π+ω2，即满足两测点船行方向相反，且在传感器坐标系下应答器位置未发生改变。

条件2θA1=π+θA2，H1=H2，ω1=π+ω2，即满足两测点船行方向相同，且在传感器坐标系下应答器位置与原位置关于原点对称。

由以上两条件可见，估值偏差的符号与船行方向及应答器的相对位置紧密相关。

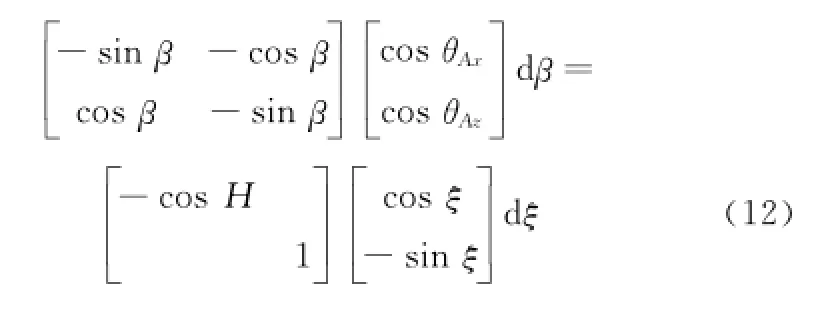
当两测点关于应答器原点对称，有dξ1=dξ2。由于应答器始终在船只下方，式（12）中cosθAz符号不变，以下情况可满足dβ1=-dβ2。

条件3θA 1=θA 2，H1=π+H2，ξ1=ξ2。，即满足两测点船行方向相反，且在传感器坐标系下应答器位置未发生改变。横摇偏角γ与式（12）的分析结果相同，此处不再详细说明。

3.2声传感器坐标系内方位角θA偏差

声传感器坐标系下的方位角θA可通过声传感器接收应答器信号时延差计算得到［1，6 7］

式中，τ为通过声学测时得到的时延差；d为准确已知的声传感器间距；C为声传感器处对应声速。超短基线定位时，其声传感器所在的表层海水温度随时间变化明显，同日内最大温差甚至超过1°C，由此产生的声速偏差可超过4 m/s［14］。即便在声传感器处增加实时测量声速以补偿表层水体声速的实时变化，声速测量设备由于长期未校准时偏差也可达到2 m/s左右［10］。当利用存在偏差的声速计算声信号入射方向角θA时，产生的传感器坐标系下方位角偏差dθA为［15］

可见声速对θA的影响与θA大小相关。在π/4方位角下，3 m/s的声速偏差将产生0.1°的方位角偏差，是影响标定精度的主要因素之一。

同样首先考虑θA偏差对艏向安装偏角α的影响，式（7）可展开为

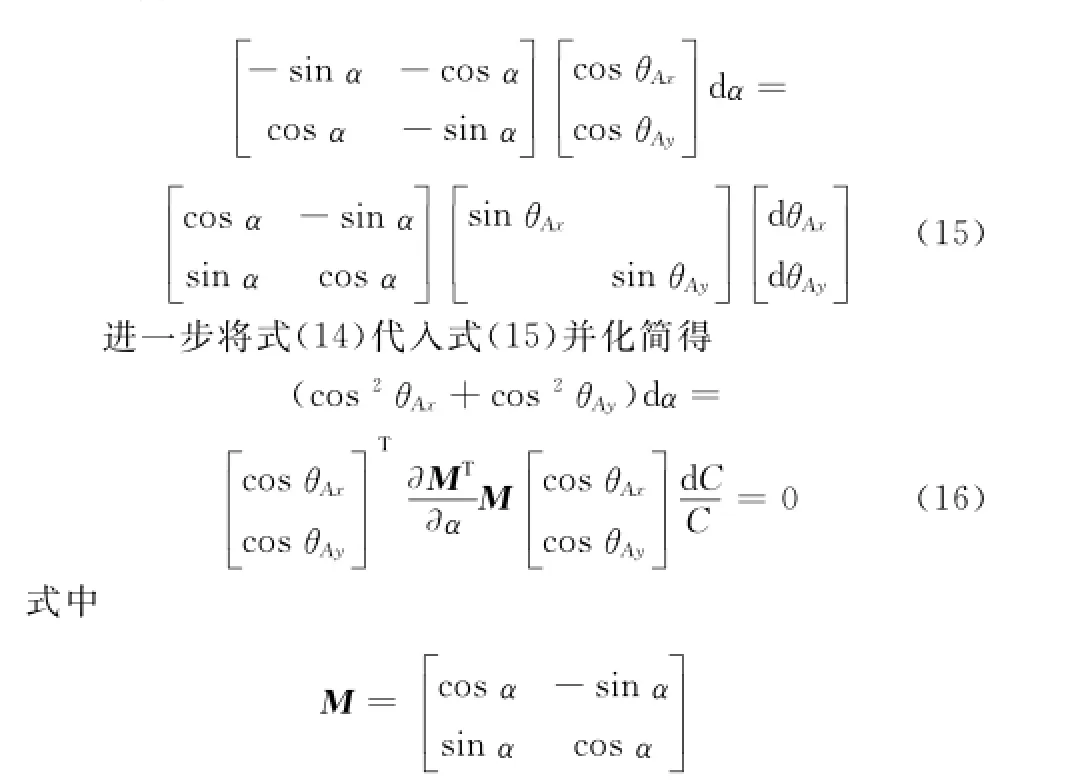
式（16）表明：声速测量偏差d C不会产生艏向安装偏角估值偏差。

对于纵倾安装偏角β受θA的影响，由于θAz是利用θAx，θAy计算得到［6 7］的，故将θAz表达为θAx，θAy的函数。此时式（7）化简为

进一步化简得到dθAx=cotθAx/C·d C。易知此时在以下情况下可满足dβ1=-dβ2使纵倾安装偏角β估值无偏。

条件4θAx1=π-θAx2，即要求在声传感器坐标系下，两测点测得的应答器x坐标反向。

特殊地，当θAx=π/2时，dθAx=0，dβ=0。即当应答器与声传感器x轴夹角为90°时，β为无偏估计。因而若以满足θAx=π/2条件的测点组成测线，也可使纵倾安装偏角β不受θA测量偏差的影响。

同理对于横摇安装偏角γ

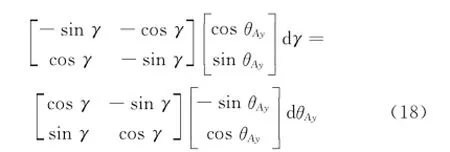
化简得dθAy=cotθAy/C·d C，则以下条件可满足dγ1= -dγ2。

条件5θAy1=π-θAy2，即要求在声传感器坐标系下，两测点测得的应答器y坐标反向。

特殊地，当θAy=π/2时dθAy=0，dγ=0。故若以满足θAy=π/2条件的测点组成测线，也可使横摇安装偏角γ不受θA测量偏差的影响。

由此针对声传感器坐标系下方位角θA偏差的影响，分别找到了能抵消艏向、纵倾、横摇安装偏角估值偏差的条件。

4　安装偏角标定测线规划

第3节分析推导时以测量的对称性为前提，再利用相同或相反的行船方向抵消安装偏角估值偏差。可见规划测线减小安装偏角估计误差本质上是利用测线的对称性与航向对固定测量偏差进行抵消。因此在规划安装偏角标定测线时首先需要保证测线对称性，并需要设计行船方向。

如图1所示的测点及航向均满足第3.1节中条件1。需要说明的是在图中4组航向间仍有多组航向满足要求，这里仅列出部分具有代表性的航向。穿过应答器上方的往返两条直线测线满足航向Ⅰ与Ⅲ，如图2（a）；以应答器为圆心的两条往返圆形测线则满足航向Ⅱ与Ⅳ，如图2（b）所示。需要说明的是，图2（a）和图2（b）中将两条本应完全重合的测线稍微错开以便于辨识。

以任意恒定航向通过应答器的直线测线均满足第3.1节中条件2，如图3所示。但此测线不满足第3.1节中条件3，说明仅利用一条直线测线标定结果仍受UTM坐标系下方位角测量偏差的影响。而图2中全部测线不仅都满足条件2，还同样满足第3.2节中条件4和条件5。因而2条重合往返的对称直线或圆测线都能抵消测量偏差的影响，使安装偏角估值无偏。此外，若将图2所示4条测线合并，也能使安装偏角估值不受测量偏差影响。

图1　满足条件1的部分测点

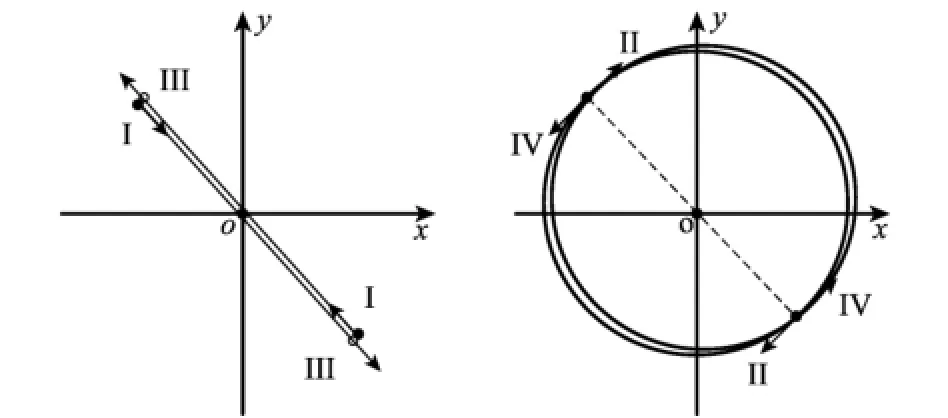
图2　图1航向对应的测线

实际测量中，非零的声传感器安装偏差、船只横摇、纵摇姿态以及操船等多种因素使得往返测线难以保证严格重合与对称。因此通过仿真评估测线在不能满足理想对称条件时的标定误差。

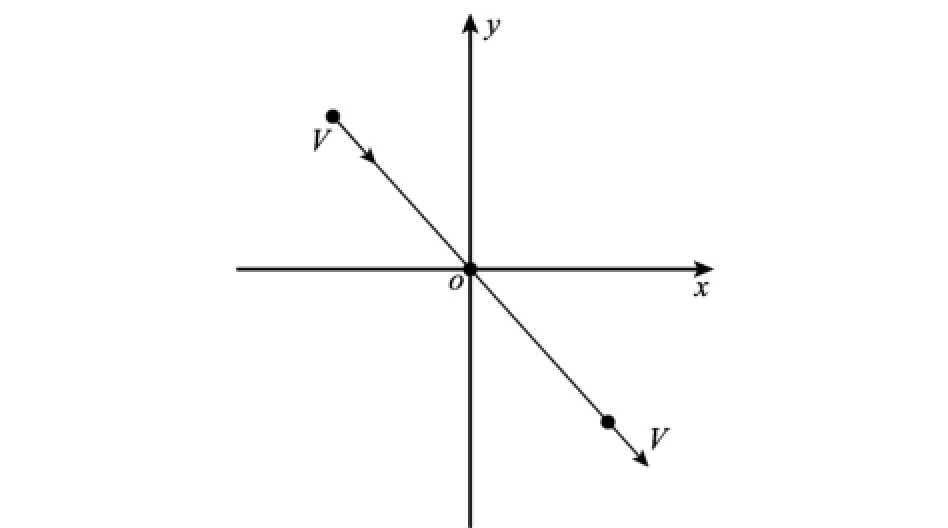
图3　满足条件2的一种测线

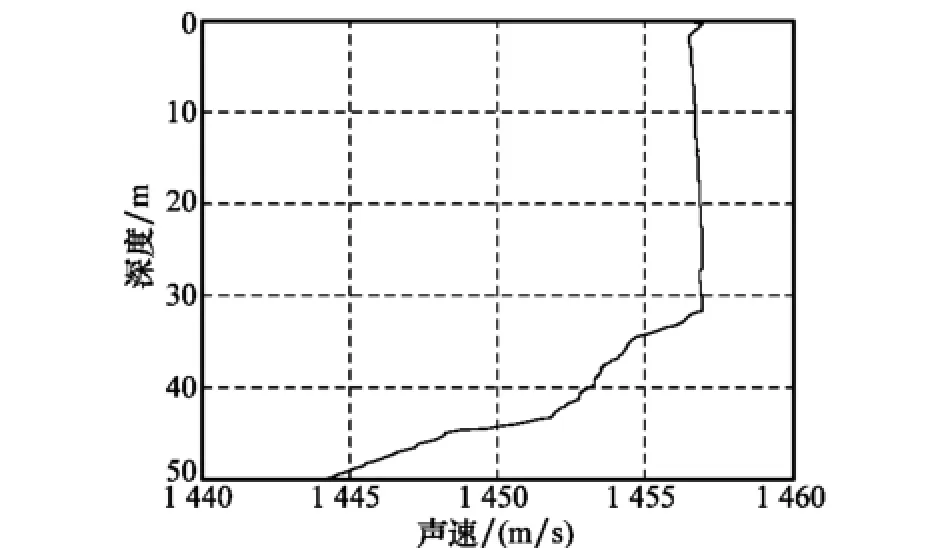
图4　仿真使用的声速剖面

仿真条件如下：应答器水平位置设为原点，深度为50 m。船只分别以图2所示的对称重合的往返直线、圆测线以及两者合并成的组合测线航行。其中直线与圆直径的长度为180 m。应答器位置固定误差设为0.5 m。仿真使用如图4所示的声速剖面，声速剖面测量偏差2 m/s。此外，仿真中还在声学测得的信号入射角度中引入了均值为0°，标准差为0.02°的高斯随机误差；在船只方位与姿态数据中引入了均值为0°，标准差为0.01°的高斯随机误差。通过1 000次独立重复计算统计得到标定结果的均值与标准差，如图5所示。图5中柱形图对应标定结果均值与真值的差值，误差棒表示标定结果标准差。跟据不同的测线将柱形图分为3组，每组包含的4个柱形图由左至右依次代表4类不同的测量情况。

（1）安装偏角Φ为零，往返测线重合；

（2）Φ=［3，-0.5，3］°，往返测线重合；

（3）Φ=［0，0，0］°，往返测线存在5 m的位置偏差与3°的夹角；

（4）Φ=［3，-0.5，3］°，往返测线存在5 m的位置偏差与3°的夹角。

通过比较以上4类情况，分析测线的标定性能。

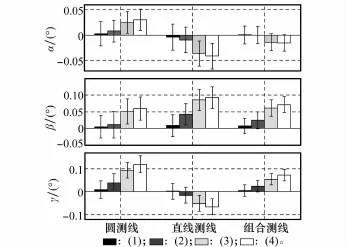
图5　仿真结果

由图5可见：当测线完全重合且安装偏角为零时（各组柱形图左一），3种测线标定所得的安装偏角均十分接近真值。当仅引入［3，-0.5，3］°的安装偏差时（各组柱形图左二），声传感器坐标系下的测量不再严格对称，标定偏差变大：其中圆测线的γ角标定结果最不准确，但α，β角标定误差变化相对较小；直线测线的β角标定结果最不准确，但α，γ角标定偏差变化相对较小，且偏差为负；由于圆测线与直线测线的α，γ标定偏差反向而部分抵消，组合测线中α角标定结果最为准确，γ标定结果与直线测线相近，β角标定误差介于直线与圆之间。引入测线偏差后，各测线的标定偏差均继续变大，以情况（4）为例（各组柱形图右一）：组合测线的α角标定最准确；直线测线γ角标定最准确，但仅优于组合测线结果0.005°；圆测线β角标定最准确，优于组合测线结果0.01°。

直线测线γ标定准确度高是由于船只沿直线朝向应答器航行只时传感器坐标系y轴与应答器的夹角接近90°，根据式（18）可知此时γ角受声传感器坐标系下测角偏差影响较小。而船只沿圆测线航行过程中传感器坐标系的x轴与应答器的夹角接近90°，根据式（17）可知该测线可保证β角受传测角偏差影响较小，标定更准确，但横摇安装偏角γ则存在较大的偏差。组合测线则通过圆、直线测线之间反向的α，γ标定偏差相抵消而提高α标定准确度，并使γ的准确度与直线测线接近。

在接近实际标定的情况（4）中，虽然直线、圆测线分别均有最高的γ角与β角标定准确度，但两者更大的标准差掩盖了其微小的准确度优势。仿真计算得出：对于γ角，直线测线的置信区间为2.934±0.034°，而组合测线的置信区间为3.071±0.025°；对于β角，圆测线的置信区间为-0.441±0.035°，而组合测线的置信区间为-0.428± 0.023°。组合测线具有更小的标准差是由于其综合了直线、圆测线中的全部数据，大量观测数据对随机误差起到了平均作用。因而考虑标准差后，即便使用圆或直线测线对β或γ角分别单独标定，其结果也不能优于组合测线。

综上，组合测线对α角标定准确度最高，β，γ角的标定准确度分别与圆测线、直线测线相当，并且组合测线标定结果具有更好的一致性。因此，综合来看，组合测线与直线、圆测线相比更适于超短基线声传感器安装偏差标定。最终将标定测线规划为由关于应答器对称的直线与圆测线组成的组合测线，并且该测线需要重合往返航行，如图6所示。

图6　规划的组合测线

5　外场试验验证

2011年10月在吉林省松花湖水库进行了超短基线系统声传感器安装偏差标定试验。试验区域平均水深50 m左右。试验平台为小型客用船。试验设备包括：哈尔滨工程大学自研超短基线定位系统及应答器，法国IxSea公司OCTANS高精度姿态测量仪，美国Leica公司GPS1200型GPS流动站与基站。试验中超短基线定位系统声学传感器安装于船右舷，入水约2m；姿态测量设备安装靠近船重心；GPS天线安装在声传感器固定杆顶端。应答器布放深度为50 m。

试验期间未对声传感器或罗经进行过重新安装。船只以3种标定测线采集数据：以应答器为圆心，半径90 m与60 m的往返圆测线各3个条次；通过应答器上方，与东方向约成60°、135°、150°与210°夹角的往返直线测线各1个条次，共10个条次的测线数据，如图7所示。

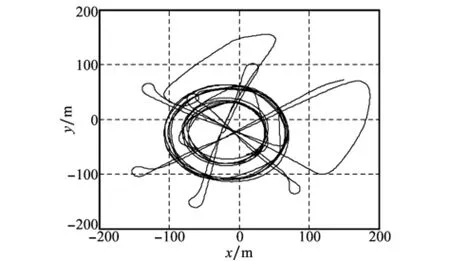
图7　试验采集的标定测线

标定计算时对图7中的测线进行了截取：分别截取了3组90 m半径往返圆测线、3组60 m半径往返圆测线；与东方向约成60°、135°、150°、210°夹角的往返直线测线各1组。进一步将6组60 m、90 m半径圆测线分别与4组直线测线组合，形成共6组组合测线。在组合过程中将保持直线测线与圆测线直径长度相同。利用3类测线分别标定计算，比较同类及不同测线之间的标定结果，如图8所示。

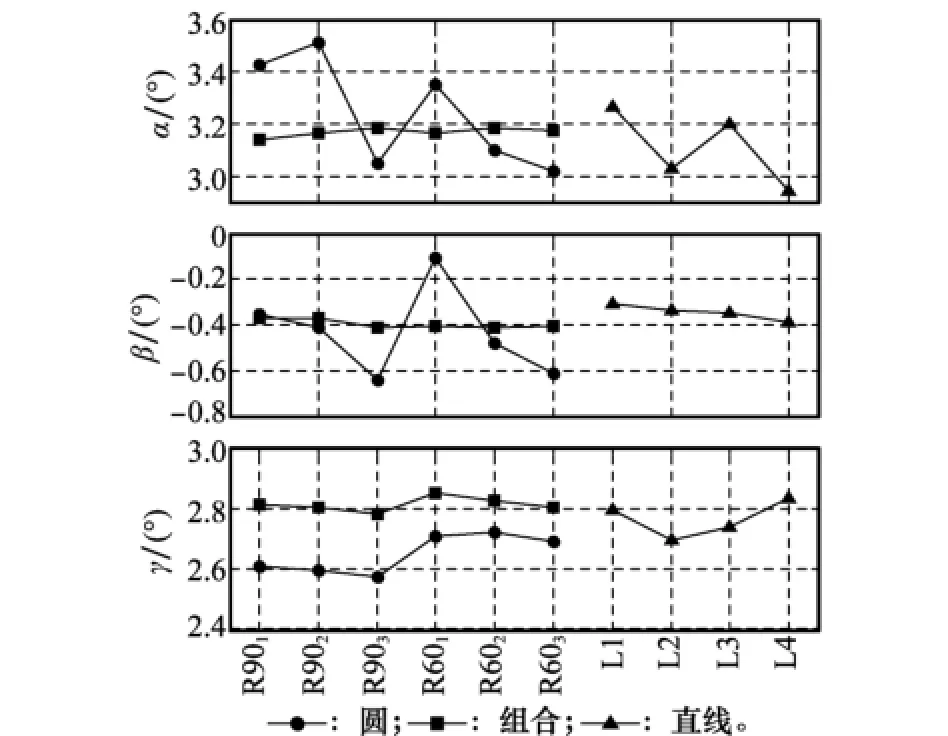
图8　湖试各类测线标定结果

图8中横坐标为测线数据的名称：圆及组合测线数据名称由 圆测线半 径及标号 组成（R901-R903，R601-R603）；L1-L4代表4组直线测线。带有圆标记线为圆测线标定结果，带有方形标记线代表组合测线标定结果，带有三角标记测线为直线测线结果。对比组合测线与其他测线结果可见：6组组合测线的安装偏角标定结果基本一致，安装偏角的标准差分别为stdα=0.017 3°，stdβ=0.019 4°，stdγ=0.024°；优于直线测线的起伏值stdα=0.148 0°，stdβ=0.033 9°，stdγ=0.059 8°。由图8可以明显分辨圆测线标定结果一致性较组合测线差。根据不同测线标定结果的一致性可见组合测线具备更优的标定性能。

进一步利用标定结果修正定位散点，以定位散点精度评价标定结果的准确性：由于在标定过程中应答器位置固定，若安装偏角标定结果更接近真值，修正后的定位散点应当更为密集。因此分别使用3类测线标定结果的均值修正全部的定位数据散点，观察经不同测线修正后的散点差别。图9（a）～图9（d）依次表示修正前定位散点、组合测线标定结果修正后散点、圆测线标定结果修正后散点、直线测线标定结果修正后散点。表1中统计了图9中散点在x，y两个方向的标准差。

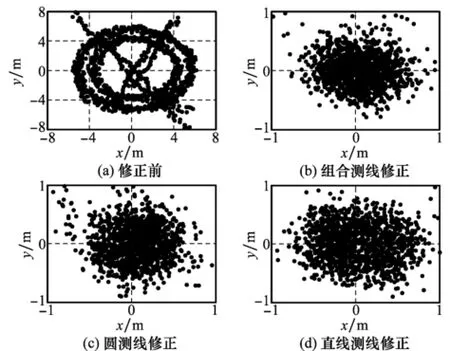
图9　标定结果修正定位散点

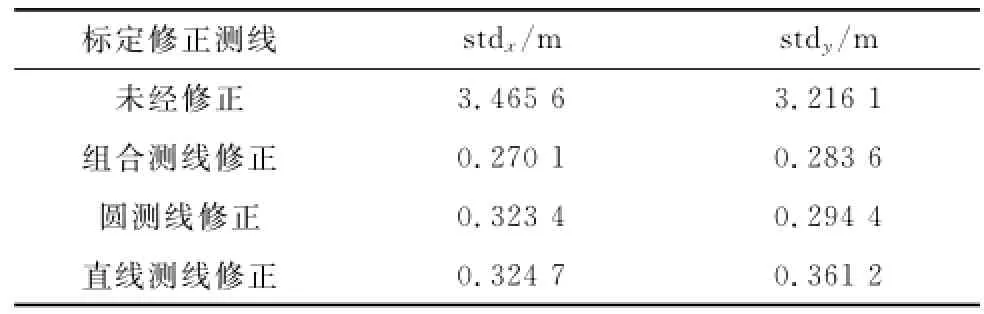
表1　定位散点标准差统计结果

由图9可见，标定修正前定位散点呈现明显的航迹图形，定位散点的标准差统计值均超过3 m，说明确实存在声传感器安装偏差。对比图9（b）～图9（d）中利用3种测线标定结果修正后的定位散点，组合测线结果修正散点最为密集，精度最高：x，y方向的标准差分别为stdx=0.270 1 m，stdy=0.283 6 m。而利用圆测线标定结果修正后，位置偏离均值0.5 m以上的散点数量增多。这是由于圆测线标定结果未能对直线测线定位数据较好修正导致的。类似地，使用直线测线标定结果修正时，图9（d）中圆测线定位散点的密集程度变差。说明单独使用圆或直线测线得到的安装偏差角度标定结果中存在更大的残差，标定准确度较组合测线低。通过不同测线标定结果修正定位散点的情况比对可以看出：使用组合测线结果时定位散点更为密集，定位精度更高，因而组合测线对应的标定结果更接近真值。

试验数据处理结果表明：当实际测量中测线难以严格保证对称、重合时，组合测线具有更好的重复标定一致性，对安装偏角标定的准确度更高。因而将超短基线声传感器安装偏角的标定测线规划为关于由直线与圆测线组成的组合测线，该测线需要重合往返航行。

6　结束语

超短基线声传感器安装偏差标定准确度与标定测线有关，因而本文以减小固定测量偏差对标定的影响为出发点，规划满足要求的测线。文章利用对称测量对固定测量偏差的抵消特性，分析并得出了能够抵消由应答器位置偏差、声速偏差对安装偏角标定影响的条件。并根据条件规划出在理想对称重合条件下能使安装偏角标定无偏的测线：直线测线、圆测线以及将两者合并的组合测线。进一步的仿真计算与试验数据处理表明，当实际测量中测线难以严格保证对称、重合时，组合测线具有更好的重复标定一致性，对安装偏角准确度更高，更适合作为超短基线声传感器安装偏差标定测线。

需要说明的是，标定测线规划是一个开放性的问题，与标定计算估计方法、计算模型、规划目的等因素有关。当以上因素改变时，对应的最优标定测线可能改变。但本文利用测量对称性减小固定测量偏差影响的研究思路与方法仍有一定的借鉴的价值。

［1］Philips D R C.An evaluation of USBL and SBL acoustic systems and the optimization of methods of calibration-Part 1［J］.The Hydrographic Journal，2003，32（4）：18-25.

［2］Philips D R C.An evaluation of USBL and SBL acoustic systems and the optimization of methods of calibration-Part 2［J］.The Hydrographic Journal，2003，32（7）：10-19.

［3］Philips D R C.An evaluation of USBL and SBL acoustic systems and the optimization of methods of calibration-Part 3［J］.The Hydrographic Journal，2003，32（10）：11-19.

［4］Chen HH.Insitu alignment calibration of attitude and ultra short baseline sensors for precision underwater positioning［J］. Ocean Engineering.2008，35（14）：1448-1462.

［5］Morgado M，Oliveira P，Silvestre C.Experimental evaluation of a USBL underwater positioning system［C］//Proc.of the Electronics in Marine，2010：485-488.

［6］Yu M，Hui J Y.The calibration of the USBL transducer array for long-range precision underwater positioning［C］//Proc.of the 10th International Conference on Signal Processing，2010：2357-2360.

［7］Chen H H.The estimation of angular misalignments for ultra short baseline navigation systems.Part I：numerical simulations［J］.The Journal of Naυigation，2013，66（4）：561-578.

［8］Chen H H.The estimation of angular misalignments for ultra short baseline navigation systems.Part II：experimental results［J］.The Journal of Naυigation，2013，66（5）：773-787.

［9］Li Z H，Huang J S.GPS surυeying and data processing［M］. Wuchang：Wuhan University Press.2005：75-121，193-201.（李征航，黄劲松.GPS测量与数据处理［M］.武汉：武汉大学出版社，2005：75-121，193-201.）

［10］Dosso S.Optimal array element localization［J］.Journal of Acoustic Society America，1999，106（6）：3445-3459.

［11］Sonardyne Company.sonardyne USBL calibration［EB/OL］.［2015-1-23］.http://www.sonardyne.com.

［12］IxSea Company.IxSea posidonia USBL calibration［EB/OL］.［2015-1-23］.http://www.IxSea.com.

［13］Zheng C，Li Z，Sun D.Study on the calibration method of USBL system based on ray tracing［J］.Oceans-san Diego，2013，71（2）：1-4.

［14］Liu B S，Lei J Y.Underwater Acoustic Theory［M］.Harbin：Harbin Engineering University Press，1993：59-86.（刘伯胜，雷家煜.水声学原理［M］哈尔滨：哈尔滨工程大学出版社，1993：59-86.）

［15］Li Z，Zheng C，Sun D.Track analysis and design for ultra short baseline installation error calibration［J］.Oceans-san Diego，2013，155（2）：1-5.

Track design for the acoustic sensor installation alignment calibration in ultra-short baseline positioning system

LI Zhao1，2，ZHENG Cui-e1，2，SUNDa-jun1，2
（1.College of Underwater Acoustic Engineering，Harbin Engineerin g Uniυersity，Harbin 150001，China；
2.Science and Technology on Underwater Acoustic Laboratory，Harbin 150001，China）

The track for ultra short baseline（USBL）acoustic sensor installation alignment calibration is designed by using the symmetric measurement to cancel estimate bias.By analyzing the influences of different angle measurement biases，symmetry and repeatability requirement that can ensure unbiased alignment estimates are obtained.Straight line tracks，round tracks and tracks combined with the former two are found to satisfy these requirements.Simulations and field trial are carried out to compare these three kinds of tracks.Comparison results show that combined tracks can provide better calibration accuracy and precision when the symmetry and repeatability requirement cannot be strictly guaranteed.Therefore，this combined track is recommended as the track for USBL alignment calibration.

ultra-short baseline（USBL）；installation alignment calibration；track design；sensor calibration

TB 56

A

10.3969/j.issn.1001-506X.2016.05.07

1001-506X（2016）05-1010-07

2015-02-22；

2015-06-22；网络优先出版日期：2015-11-18。

网络优先出版地址：http：//www.cnki.net/kcms/detail/11.2422.TN.20151118.1207.006.html

国家高技术研究发展计划（863计划）（2012AA091401，2010AA093901）资助课题

李昭（1987-），男，博士研究生，主要研究方向为水声定位与导航技术。

E-mail：lizhao0517@sina.cn

郑翠娥（1982-），女，讲师，博士，主要研究方向为水声定位与导航技术。

E-mail：zhengcuie@hrbeu.edu.cn

孙大军（1972-），男，教授，博士，主要研究方向为水声定位与导航技术、水声通信、水下目标探测。

E-mail：sundajun@hrbeu.edu.cn