求解资源受限多项目调度的改进遗传规划算法
陈浩杰 丁国富 张 剑 阎开印
西南交通大学机械工程学院先进设计与制造技术研究所,成都,610031
0 引言
资源受限项目调度问题(resource constrained project scheduling problem , RCPSP)[1-2]是项目管理中最为经典和核心的NP难问题[3],但RCPSP并不完全适用于众多复杂实际场景,故需要进行不同方面的扩展,如多技能RCPSP优化[4]、多模式RCPSP优化[5]等,其中资源受限多项目调度问题(resource constrained multi-project scheduling problem, RCMPSP)是应用最广泛的扩展模式[6-8],项目管理中约90%是在多项目下进行的[9]。
近年来,RCMPSP的求解方式主要以元启发式(如进化智能算法)和启发式(如优先级规则)为主。在元启发式的研究中,XIN等[10]提出了一种遗传算法,其编码方式基于活动优先级且在搜索过程中结合存储邻接矩阵,从而提高了搜索能力且避免产生非法解修复过程。ZHENG等[11]设计了一种多智能体架构,并结合关键链技术以求解分布式RCMPSP。TIAN等[12]通过研究单项目、多项目和活动等三个层次的资源流特性,提出了一种适用于求解RCMPSP的改进关键链技术。PREZ等[13]提出了一种求解RCMPSP的多模态遗传算法,通过扩展搜索过程中的种群多样性来避免算法陷入局部最优。
大量研究表明,PR调度具备快速响应能力和良好的求解能力,但不同的PR具备不同的特性导致其适用的目标函数和场景不同,且PR本身不具备优化能力,因此考虑根据不同PR的优势去构造适用更广、求解能力更强的PR。于是超启发式的理念被提出和逐步应用[19]。
遗传算法是具备很强通用性和优化能力的元启发式算法,其优化过程被模拟到超启发式算法上形成遗传规划算法(genetic programing,GP)和基因表达式编程(gene expression programming,GEP)。GP和GEP的进化过程相似,主要区别在于个体的编码方法和结果的表达[20]。在调度领域,GEP的应用主要集中在作业车间调度(job shop scheduling,JSP)[21-22]。针对项目调度,JIA等[23]提出了一种求解RCPSP的GEP框架。相比而言,GP在项目调度中的应用更广泛。CHAND等[24]将GP运用到RCPSP求解并成功进化出了调度求解能力更强的PR。在此基础上,CHAND等[25]考虑了资源扰动下的RCPSP,再次验证了遗传规划的有效性和适应能力。LIN等[26]设计了一种双层超启发式遗传规划算法求解多技能RCPSP,通过高层的超启发式算法搜索更好的低层启发式算法。
综上所述,现有研究已经成功将GP运用于RCPSP,但据文献调研并未发现GP在RCMPSP问题上的应用。相较于RCPSP,RCMPSP具备项目层的优先级属性,且由于不同项目之间的资源抢占和冲突会导致资源需求方面的属性选取受到影响,GP的有效性需要进一步验证;同时,现有RCPSP超启发式调度的研究均是优化单目标,而实际场景中多目标优化的目标间竞争关系会为优化带来额外困难[27],并且超启发式编码的特性使传统GP在搜索过程中容易陷入局部最优。基于此,本文提出一种应用于多目标RCMPSP问题的改进遗传规划(improved genetic programing,IGP)算法。
1 问题描述
RCMPSP是调度由n个项目组成的项目集P={1,2,…,n}来满足某个/些目标最优,其中每个项目i∈P都由z+2个具备有向无循环逻辑关系的活动Ai={ai0,ai1,…,ai(z+1)}构成,其中活动ai0和ai(z+1)为虚拟活动,表示项目i的开始和结束。在n个项目的执行过程中,共需要K种共用可更新资源,每种资源k(k∈K)的最大单位供应量为Rk,且设定在执行中的任意时刻t处于执行的活动集合为Et。对于任意活动aij∈Ai,j={0,1,…,z+1},sij为开始时间,dij为持续时间,Sij为紧后活动集合,rijk为活动aij对资源k的需求量。衡量RCMPSP的调度优劣通常是依据完工时间[14-16],根据文献[15]采用两个目标函数值分别从项目和项目集两个角度进行PR的性能评估——平均项目完工时间偏差Q1和项目集完工时间偏差Q2。设项目i的关键路径长度为Li,实际调度后所得到的完工时间为Ci,RCMPSP的数学模型如下:
min(Q1,Q2)
(1)
(2)
(3)
s.t.
sib-sij≥dij
(4)
di0,di(z+1)=0ri0k,ri(z+1)k=0
(5)
(6)
i∈Pb∈Sijj∈Aik∈Kt∈{0,1,…}
其中,式(4)表明项目内部各活动的紧前紧后关系,即活动必须在其所有紧前活动完成后才能开始;式(5)为虚拟活动约束,即所有虚拟活动都不需要任何资源且持续时间为0;式(6)为资源约束,即在任意时刻,处于执行状态的活动所需资源之和不得超过该类资源的最大供应量。目标函数式(1)表示采用非支配解的方式优化评估,如下所示:
(7)
式中,z1、z2表示两个不同的求解策略。
当式(7)中的不等式至少有一个严格小于时,称z1支配z2,记z1≻z2。若策略z不受到其他任何策略的支配,则z是非支配解。本文的优化目标是优化生成一组应用于RCMPSP的非支配混合优先级规则(hybrid priority rule, HPR),HPR构成的集合称为Pareto解集(非支配解集)。
2 求解RCMPSP的IGP
WANG等[15]认为,不同PR求解多目标下的RCMPSP,Q1目标最优的PR是最小项目及活动持续时间之和规则,Q2目标最优的PR是最大紧后总数规则,而BROWNING等[14]认为,在不同的问题约束或验证算例下,调度RCMPSP最好的PR往往不同。可以看出,单一的PR调度时存在一定的局限性,因此需要通过训练生成适合求解RCMPSP的调度性能优、通用性强的PR。为进化出求解RCMPSP的更优PR,本文提出了一种IGP算法,其流程如图1所示,收集多种不同工况数据并将其分为训练集和测试集,通过IGP训练后得到Pareto解集,再将Pareto解集的各PR在训练集和测试集上验证。
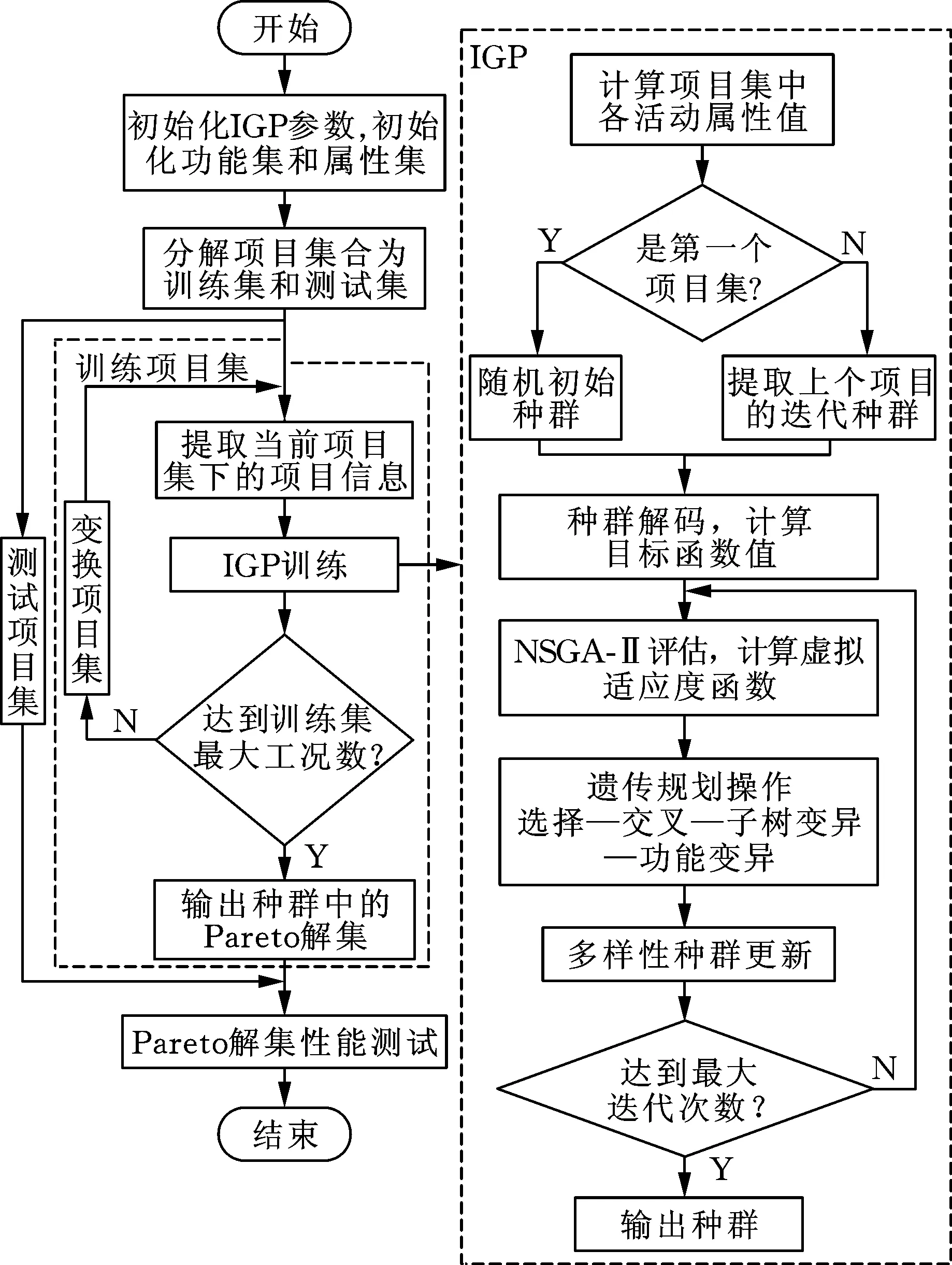
图1 IGP流程图Fig.1 Flow chart of IGP
2.1 编码设计及初始化种群
不同于启发式或元启发式算法直接得到问题的解,基于超启发式算法的IGP是为了得到求解问题的进化/混合PR。IGP基因是通过各种优先级属性经过一定的功能运算符组合后得到的,为了应用于RCMPSP求解,首先需要建立优先级属性集。在项目调度中优先选择哪个活动主要是根据活动本身的时间、活动的资源需求和活动在项目中的逻辑关系。在RCPSP中只需要考虑活动层面和资源层面的属性计算即可,而RCMPSP则需要在多个项目的不同活动之间做出决策,因此需要考虑项目层的属性。通过分析现有的20种PR[14-16]可知,项目关键路径长度在多项目调度中是主要决策依据,因此本文在RCPSP超启发式属性集[24]上增加了项目关键路径长度,从资源、活动和项目的角度提取了10个优先级属性,并对属性进行归一化处理,如表1所示。在RCMPSP中需要在同一时刻决策来自多个项目的活动,因此活动时间相关属性及关键路径长度采用最大最小归一化方式;各个活动的逻辑关系只与本项目有关,在衡量活动重要程度归一化(如Nts和Ntcs)时只考虑与本项目活动总数的比值;不同项目之间存在资源抢占,在衡量资源的归一化(如Rmax和Ravg)时采用公共资源的最大供应量比。功能集选择的超启发式最常用的六种功能运算符为“+”、“-”、“×”、“/”、“max”和“min”。
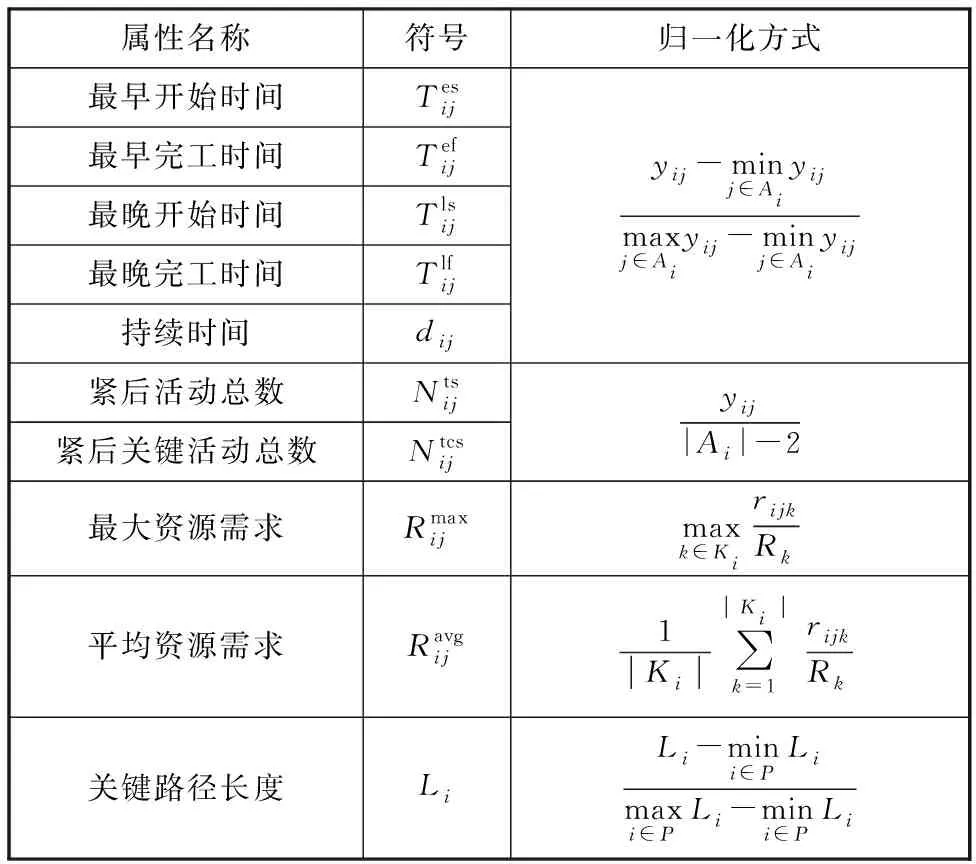
表1 优先级属性
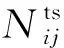
根据IGP流程,在第一个项目集下训练时需要随机初始化种群,随机初始化种群中每个个体的顶层编码以0.5的概率控制为Fall或Rise,下层结构树则采用ramped half-and-half方法随机生成,除顶层外,树深度控制在2~6之间[29],图2所示的树的深度为3。
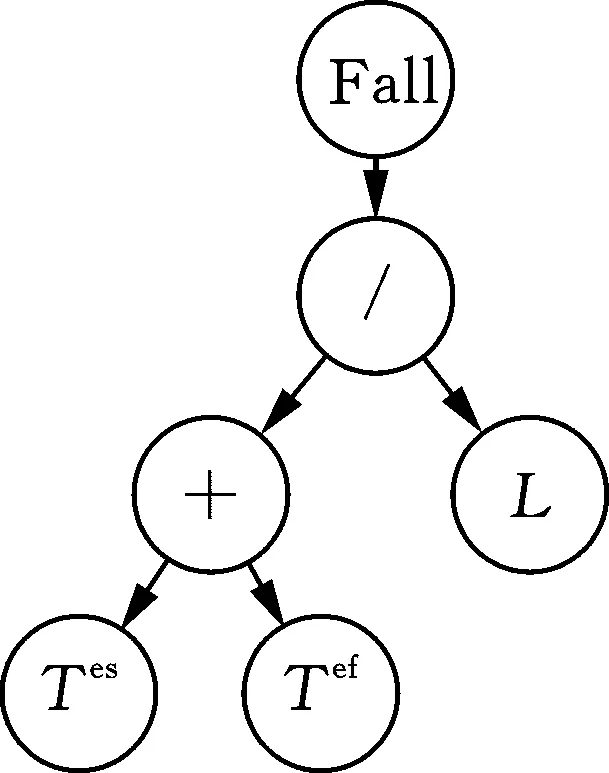
(a)降序编码结构
2.2 NSGA-Ⅱ评估和遗传算子
IGP是应用于多目标RCMPSP下的求解PR训练,因此需要建立相应PR的评估方式来实现进化过程中的基因取舍。多目标优化问题可以对每个目标赋予相应的权重转化为单目标问题,但在大多数实际场景中,权重很难确定且可能变化,因此本文采用NSGA-Ⅱ[30]来分配虚拟适应度以实现PR个体评估,主要步骤如下。
(1)根据种群中个体计算的目标函数值,将整个种群进行分支配解分层,同层的解为非支配关系,上层个体支配下层个体,不同层级解的关系如下所示:
G1≻G2≻…≻Gg≻…≻Gm
(8)
式中,m为当前种群分层后的最大层数;Gg为第g层个体。
(2)计算相同等级各个个体间的拥挤距离,由于不同目标同样数量级不同,所以仍然需要归一化,其计算公式如下:
(9)
式中,V为目标函数集合;ov,a为个体a在目标函数v下的值,下标a+1和a-1代表在目标函数值v下该非支配层中经排序后个体a的相邻个体。
(3)根据支配等级和空间距离分配其虚拟适应度,即首先判断个体所属非支配层,层级越低越优,处于相同层级的个体拥挤距离越大越优。
除了PR个体的评估,在IGP的进化过程中需要用到传统遗传算子选择、交叉和变异。其中选择算子采用锦标赛选择[31];根据文献[24],交叉算子采用子树交叉模式,即随机数小于交叉率Pc时,两父代个体交换部分子树,而变异算子则是当随机数小于变异率Pm时,用一个随机生成的子树替换父代个体某一节点下的子树。此外,配合顶层判别编码方式,在变异算子中增加判别变异方式,即当随机数小于Pm时,父代个体的顶层编码方式发生变化,如Fall编码变化为Rise编码,遗传算子的执行顺序如图1所示。
2.3 多样性种群更新
GP树状的编码方式会使整个种群出现许多功能相似或相同但结构不同的编码,如图3所示。其中图3a和图3b虽然是两种结构不同的编码,但最终产生的优先级表达式是一致的;而图3c和图3d则是对同一个优先级表达值Tef进行平方和加倍处理,在调度过程中各个活动的Tef值相对大小是固定的,因此2Tef和(Tef)2的调度排序效果也是一致的。也正是因为上述两种情况,传统GP在进化搜索过程中因种群的多样性降低而易陷入局部最优,导致训练效果不佳。为此本文设计了一种种群更新方式,在更新过程中建立虚拟适应度FK存储上一个工况的信息,作为更新是否舍弃当前个体的依据,以提升泛化性能。假设种群规模为Size,主要步骤如下:
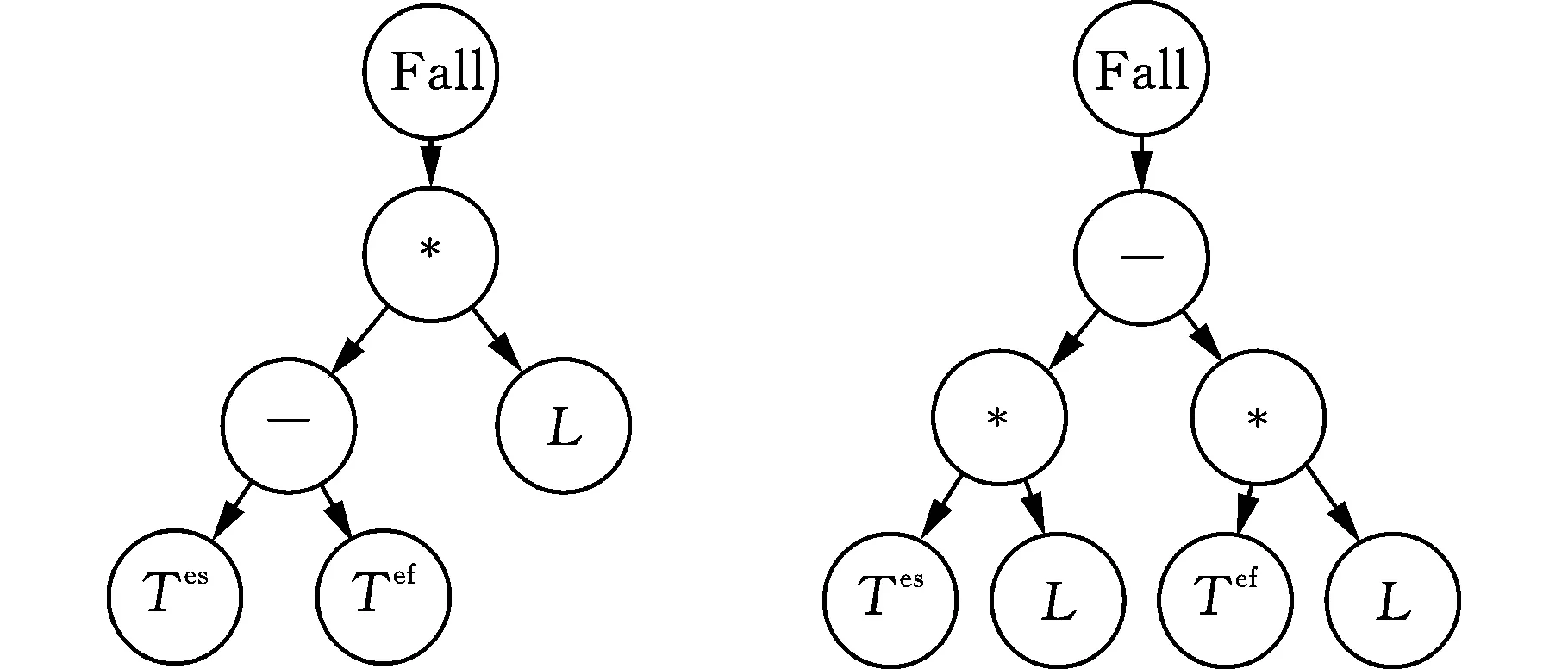
(a)相同功能结构PR1 (b)相同功能结构PR2
(1)建立相同个体临时储存集合Snew、Sold和不同个体临时存储集合D,计算遗传算子更新后的新种群中每个子代个体的各个目标函数值,如果原种群中没有目标函数值完全相同的父代个体,则该个体放入D,否则该子代个体的FK置为空(非支配层为0,拥挤距离为0)并放入Snew,对应的相同父代个体放入Sold。
(2)对于属于Snew中的每个子代个体,解析其优先级表达式是否与对应的相同父代个体一致或相似,如果否那么将该子代个体移入集合D中。
(3)对于Snew中余下各个子代个体,判断其对应父代个体FK是否为空,如果为空且随机产生的判断数小于0.5.则将该子代移入集合D中。
(4) 将D中的个体与原种群合并,选择前Size个虚拟适应度最好的个体生成下一代种群并判断是否为当前工况下的最大迭代次数,如果是,则将最终种群各个个体的虚拟适应度设置为该个体的FK值。
3 IGP性能验证及比较
3.1 实验环境和参数设置
IGP基于MyEclipse 2017开发,计算机配置为2.80 GHz双核处理器,8 GB内存。根据文献[16],一个工况的项目集由4个活动数量不同的项目构成,分别来源于PSPLIB数据库[32]中的J30、J60、J90和J120库(每个项目包含30、60、90、120个非虚活动),且项目集每种资源的最大单位供应Rk为20。选择PSPLIB数据库4个活动库的前50组数据构成验证数据集,其中前30组为训练项目集,其余为测试集。IGP中所需参数根据经验设定为:最大迭代次数Mgen=20,种群规模Size=200,交叉率Pc=0.9,变异率Pm=0.2。
3.2 评价方式
参考文献[15],采用性能排名对PR进行评价,即不同的PR调度同一个工况项目集时,根据目标函数的大小产生两组排名(Q1和Q2),用50组项目集下的平均排名W衡量PR调度性能的相对优劣,计算方式如下:
(10)
式中,M为项目集的总数量;wm,v,l为规则l在项目集m下调度目标v对应的排名值,其值为小于|Nrule|的正整数;Urule为参与排名的规则集合。
3.3 算例下IGP性能分析
IGP的训练结果为一组HPR(Pareto解集),采用IGP训练10次,将第一次训练产生的HPR与20种经典PR[15]的性能进行对比,如表2所示。表2中HPR1至HPR10为本次训练得到的10种不同结构的HPR。10次训练结果的统计表见表3。表3中,Npar为该次实验得到的非支配HPR的数量,pdo为该次实验训练出的HPR的W值高于20种传统PR的W值占所有非支配HPR的比例。
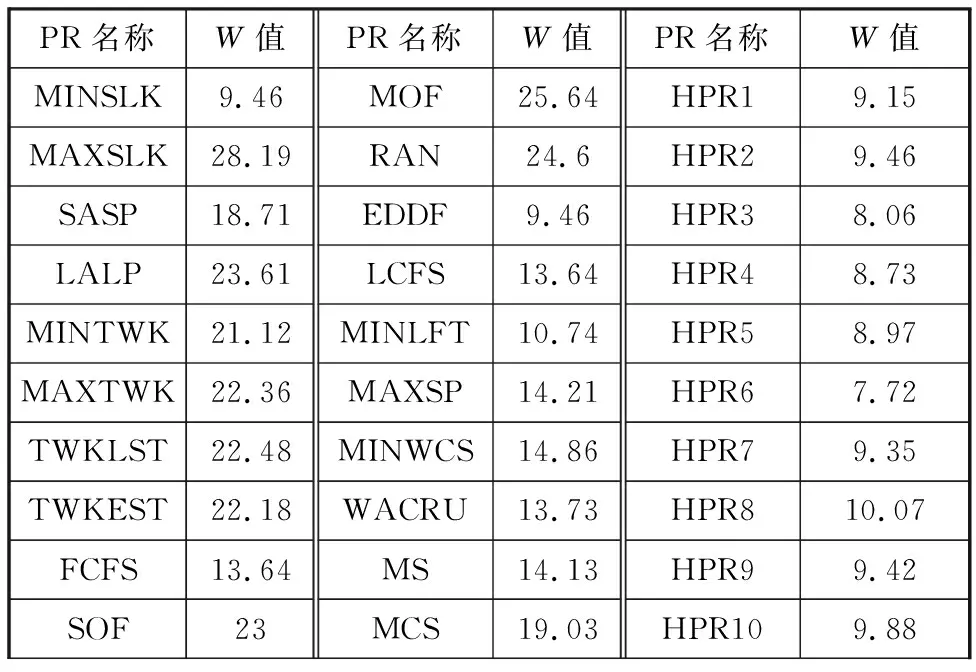
表2 传统PR和HPR的W值
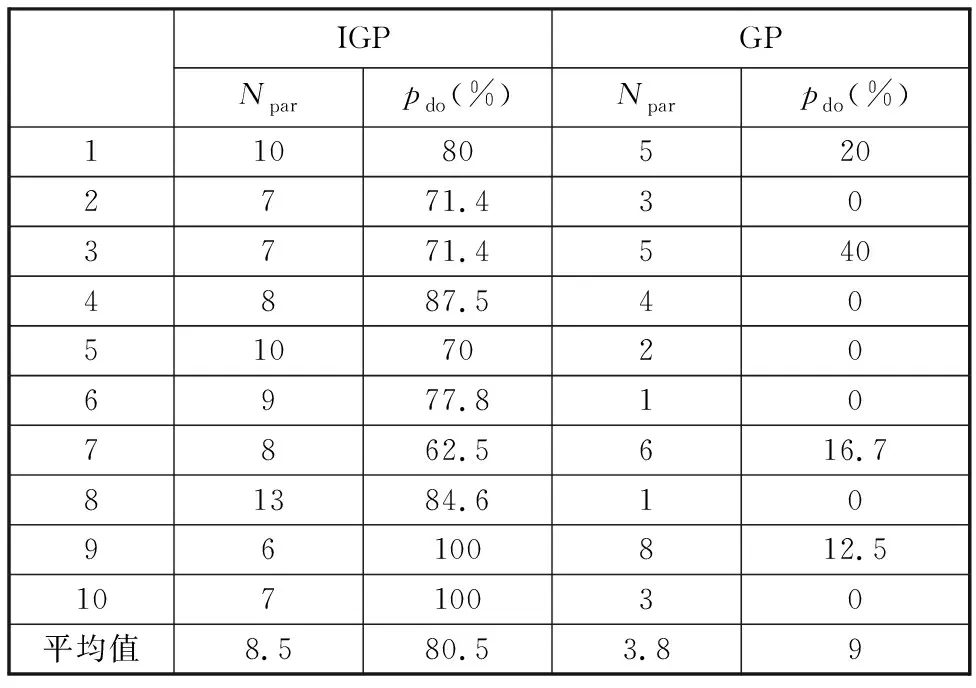
表3 HPR性能排名结果统计表
从表2中可以看出,IGP本次训练得到的80% HPR(除HPR8和HPR10外)性能排名均高于20种传统PR,而HPR8和HPR10性能排名仅次于EDDF和MINSLK两种规则。从表3中可以看出,10次训练产生的HPR优于20种传统PR的占比平均值大于80%,而剩余20%规则也优于大部分传统PR(表2),由此可以得到IGP训练的HPR调度能力比单一传统PR更优秀,证明本文提出的IGP既保留了基于启发式的PR的快速响应能力又解决了PR不具备优化能力的问题。
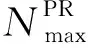

表4 HPR的Pareto前沿次数统计结果
从图4中可以看出,相较于传统PR,本文提出的IGP生成的HPR普遍目标函数值较小,处于支配地位。同时图4中的Pareto前沿(Pareto前沿为HPR2、HPR5、HPR9、HPR4、WACRU和MS)大部分是IGP生成的HPR。从表4中可以看出,大多数训练情况下,HPR的Pareto前沿次数最大值要远高于传统PR,同时平均有70%的HPR出现Pareto前沿的次数高于20种传统PR,证明了IGP的有效性。
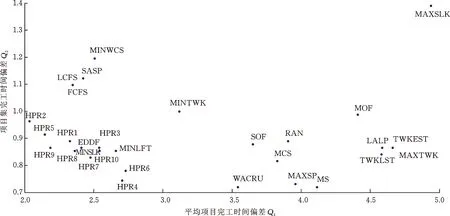
图4 工况1下不同PR和HPR目标函数支配关系Fig.4 Objective function domination relationship of different PR and HPR under condition 1
现有GP超启发式求解调度文献较少,文献[24-26]的重点在于GP在不同RCPSP问题上的实现,并非对GP的进化过程做出改进。为此,对比表3和表4可进一步证明本文提出的IGP训练的有效性。从表3中可以看出,IGP训练得到的Pareto解集中HPR的平均数量是8.5而GP为3.8,可以得出IGP能够训练出非支配解的范围更广,而GP由于相同/相似功能编码的存在,非支配解的范围大大降低。GP训练的HPR支配20种传统PR的占比平均值为9%,远低于IGP,可以看出本文提出的IGP的训练能力更强,更容易避免局部最优。从表4中可以看出,对于相同的传统PR,GP生成的HPR的支配能力低于IGP,其Pareto前沿出现的次数较低甚至在某些训练下要弱于传统的PR。由此可以看出IGP训练的HPR具备更强的通用性。
为进一步验证IGP训练出的HPR比现有启发式算法具备更强的调度能力,选择文献[18]中的启发式PSGS-SLK进行对比。第一次IGP训练的HPR与PSGS-SLK调度50组算例的支配关系如表5所示,其中Nd为HPR支配PSGS-SLK的算例个数,Nnd为二者互为非支配关系的算例个数,Npd为PSGS-SLK支配HPR的算例个数。10次训练后的结果统计表如表6所示,pd代表支配算例个体大于被支配算例个数的HPR(即Nd大于Npd)占该次训练的所有HPR的比例。
通过表5和表6可以看出,大多数的HPR能够实现大部分工况支配PSGS-SLK或与其成非支配关系,表明相较于现有的启发式算法,IGP所训练的HPR具备更好的调度能力。
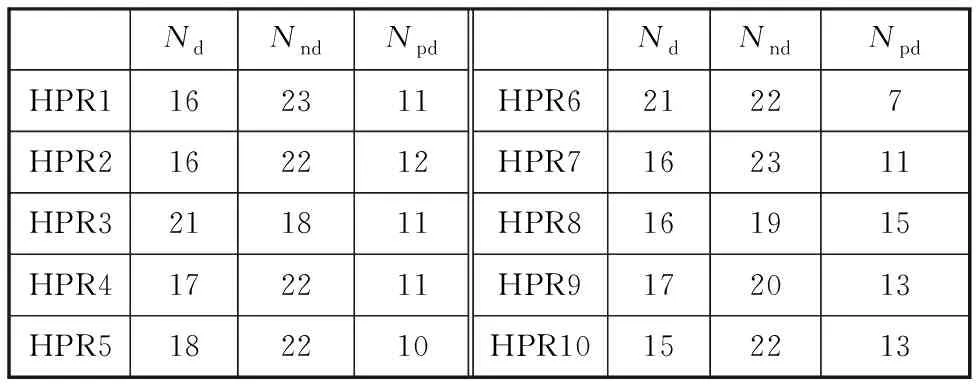
表5 HPR与PSGS-SLK支配关系表
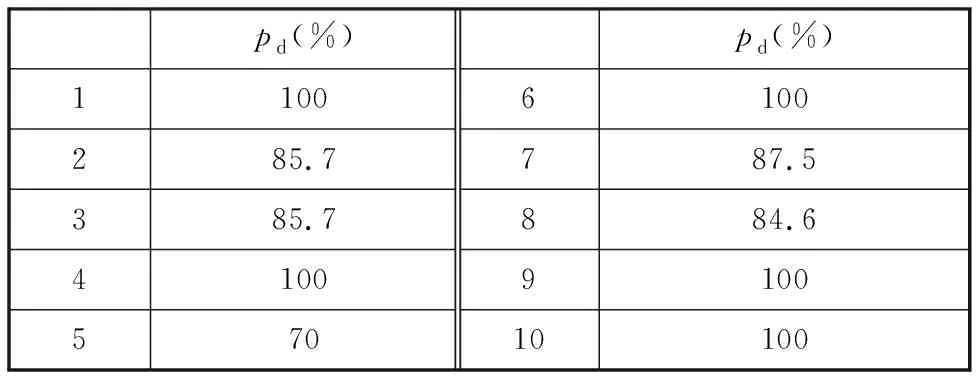
表6 HPR与PSGS-SLK支配关系统计表
3.4 实例下IGP性能验证
本文以某飞机总装厂机电调试部分装配作业为例对算法进行验证。该厂采用两条并行装配线装配两种不同机型的飞机且均包括机电调试作业,对于同一架次飞机而言,该部分的调试工作会影响后续的装配工作,因此既要考虑本架次飞机该工位的装配时间最短又要考虑两架飞机的总装配时间最短。该部分装配工作需要共用同一班组人员(总人数为18)和3种公用工装(总数均为10)。两种机型机电调试装配作业的紧前紧后关系及所需资源通过扫描本文首页OSID二维码可见,该厂目前以最晚开工时间为优先级进行生成调度,即EDDF。通过关键路径法可得项目1和项目2的关键路径分别为50和55,而IGP第一次训练后的HPR和EDDF的调度结果见表7,10次训练结果见表8。表7中,C1和C2分别为项目1和项目2的完成时间,表8中Pd为支配EDDF的HPR占总的HPR的比例,Pnd为与EDDF互为非支配关系的HPR的比例。
从表7中可以看出,IGP生成的大多数HPR的调度性能要优于EDDF,且剩余HPR和EDDF相比各有优势,在未分配权重时互为非支配关系,由此可以证明IGP能够为RCMPSP调度带来更多有效的HPR。在表8的统计结果中,除第7次训练和第10次训练IGP产生了EDDF支配的HPR(分别占比12.5%和28.6%)外,其余HPR均为支配EDDF或与EDDF互为非支配关系,且在大多数训练情况下IGP生成的HPR支配EDDF的概率较大,验证了本文提出的IGP在实例调度中的有效性。
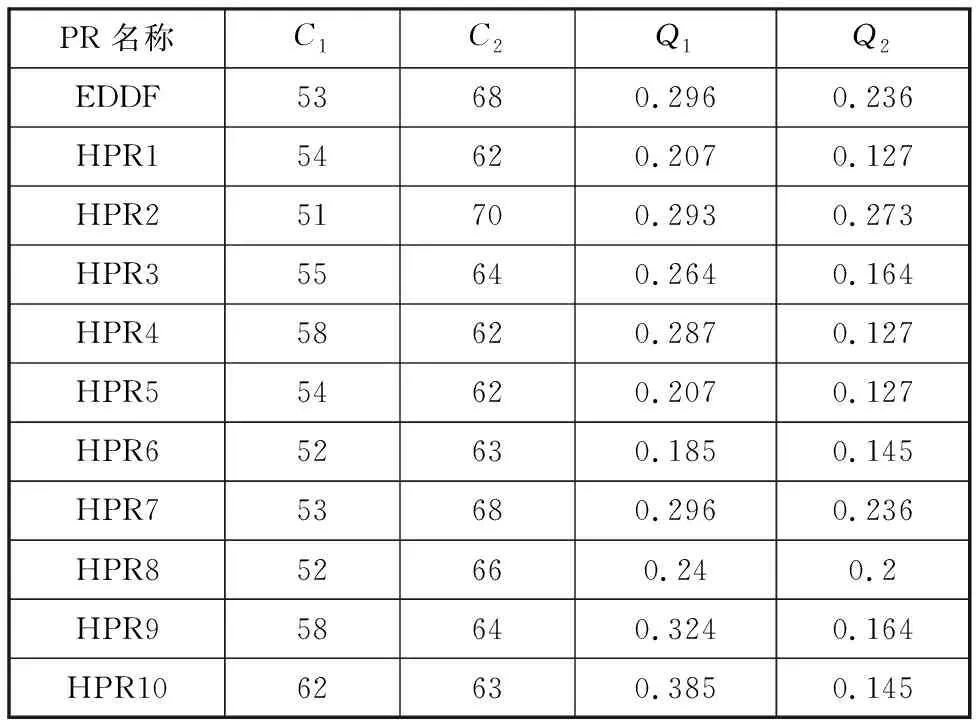
表7 HPRs和EDDF的调度结果
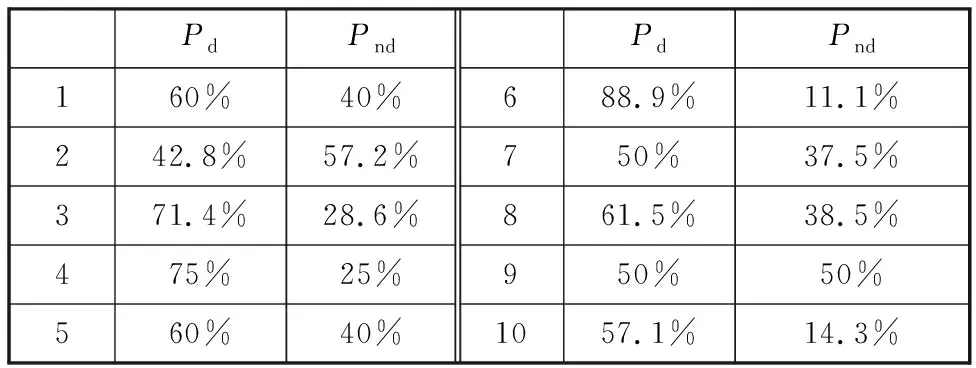
表8 HPR与EDDF的训练结果
4 结论
为了实现多目标RCMPSP下的PR最优进化,本文对GP进行改进,提出一种IGP算法:
(1)通过现有的20种求解RCMPSP问题的PR,从资源、活动和项目的角度提取属性,并根据属性的类型设计了不同的归一化方式,同时设计了判别编码,确保最小化/最大化同一种优先级表达式均能迭代搜索,从而保证解空间的完整性。
(2)结合NSGA-Ⅱ的虚拟适应度分配的评估方法,不设置权重而是对种群中个体进行非支配分层并计算不同层个体的拥挤距离,从而评估个体的优劣。
(3)设计了一种多样性种群进化更新方式以消除相同/相似功能编码,避免传统GP容易陷入局部最优的问题,提高了算法的搜索能力和泛化能力。
下一步研究可将该方法应用在动态RCPSP类问题下求解并结合鲁棒性性能分析,使其获得更广泛的应用和达到更全面的快速求解。

