几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响

席静谣 周长光 冯虎田 张鲁超

南京理工大学机械工程学院，南京，210094

0 引言

滚珠丝杠副是实现力与力矩转换的传动装置，具有承载能力强、刚性高、定位精度高、使用寿命长等[1]优良特性，近年来被广泛应用于航空航天、军工核电等领域。滚珠丝杠副载荷分布是直接影响承载能力和刚性的关键因素，对其进行研究与优化可有效提高滚珠丝杠副的机械性能[2]。滚珠丝杠副的结构参数与材料特性决定了其载荷分布情况，但由于加工过程存在因制造精度、热变形等因素带来的滚珠尺寸误差、丝杠导程误差以及滚道齿形误差等几何误差，所以每个滚珠实际受力情况各不相同[3]。在滚珠丝杠副的使用过程中，自由端的移动(固定-支撑安装方式)会导致丝杠受到额外的倾覆力矩，同样会造成滚珠受力不均的现象[4]。因此,研究几何误差和倾覆力矩对双螺母滚珠丝杠副载荷分布的影响具有重要意义。

国内外学者在滚珠丝杠副摩擦[5-6]、温升预测[7]、寿命预测[8-9]和健康诊断[10-12]等方面进行了大量研究。在滚珠丝杠副载荷分布研究方面，WEI 等[13]建立了滚珠丝杠副动力学模型并分析了转速对接触力的影响，但是模型中假设所有滚珠受力相同；CHEN等[14]得到了基于完整滚动体的单螺母滚珠丝杠副的载荷分布，结果表明每个滚珠的法向接触力是逐渐递减的。LIN[15]采用数值计算的方法对滚珠丝杠副的受力情况进行仿真，发现每个滚珠的法向力各不相同，但其变化趋势并不是单纯的递减，而是存在一定的波动情况。BERTOLASO等[16]采用光测弹性仪与标记追踪技术对承载状态下每个滚珠的位移量进行监测，并以此计算出其法向接触力，试验结果表明滚珠的法向接触力逐渐减小。LIU等[17]建立了一种考虑倾覆力矩的单螺母载荷分布模型，并分析了螺母位置对载荷分布的影响。以上研究在计算滚珠丝杠副载荷分布时未考虑误差的影响，因此模型在应用时会出现一定偏差。

MEI等[18]在考虑丝杠和螺母的变形情况下，分析了几何误差对单螺母滚珠丝杠副的载荷分布的影响。ZHEN等[19]和ZHAO等[20]建立了轴向载荷和力矩作用下的单螺母滚珠丝杠副载荷分布模型，并分析了滚珠尺寸误差对丝杠副疲劳寿命的影响。LIN等[21]对单螺母滚珠丝杠副载荷分布的研究考虑了几何误差带来的影响，但计算过程中只针对一个滚珠施加了几何误差，误差值并不随机，且误差被直接转化为滚珠尺寸的变化，计算的准确性仍需验证。以上研究虽然考虑了尺寸误差对单螺母滚珠丝杠副载荷分布的影响，但是计算过程中将导程误差、齿形误差转化为滚珠尺寸误差，且误差值并不随机，因而计算结果与实际情况仍有差异。

综上所述，目前关于滚珠丝杠副载荷分布的研究主要集中在单螺母，对双螺母载荷分布的研究则相对较少。为此，本文建立了一种考虑几何误差(滚珠尺寸误差、丝杠导程误差和滚道齿形误差)和倾覆力矩的双螺母滚珠丝杠副载荷分布模型。

1 载荷分布模型的建立

本文在建立双螺母滚珠丝杠副载荷分布模型时，作如下假设：①滚珠与丝杠、螺母滚道的接触变形均在弹性范围内；②丝杠和螺母滚道的曲率中心与滚珠的中心在同一直线上；③忽略滚珠与滚道之间的摩擦。如图1所示，在一端固定一端支撑的安装方式下，滚珠丝杠副会受到倾覆力矩的作用，导致丝杠轴线与螺母轴线存在一定的偏角。为了便于分析，假定两个螺母固定，且丝杠顺时针方向倾斜为正，Fa是轴向外载荷，Fp是预紧力，T是丝杠受到的倾覆力矩，θ′是丝杠轴线与螺母轴线之间的倾斜角。滚珠与滚道的接触状态见图2，可知，螺母A和螺母B分别受到轴向外载荷和预紧力的共同作用，其轴向力与每颗滚珠的法向接触载荷之间的关系为

(1)

(2)

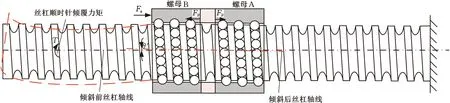
图1 在倾覆力矩作用下丝杠与螺母的相对位置图Fig.1 Diagram of the relative position of the screw and nut under the overturning moment

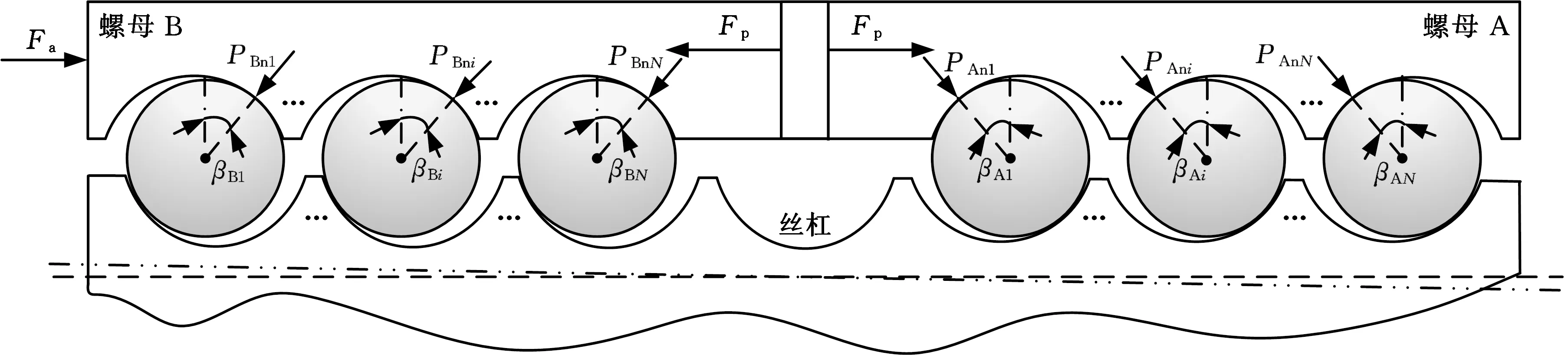
图2 轴向载荷较小时滚珠与滚道的接触状态Fig.2 The contact state of the ball and the raceway under the small axial load

未施加轴向外载荷时，两个螺母仅受预紧力作用，此时滚珠所受法向接触载荷分别为

(3)

(4)

式中，PAni0、PAsi0、PBni0、PBsi0为仅在预紧力作用下各个滚珠在丝杠、螺母接触点处的法向接触载荷；β0为初始接触角，β0=45°。

由赫兹弹性接触理论可知，滚珠与丝杠或螺母滚道的接触区域呈椭圆形，滚珠法向接触载荷与滚珠变形量δi0之间的关系为

(5)

(6)

(7)

式中，ks(e)、kn(e)分别为滚珠与丝杠和螺母接触椭圆的第一椭圆积分；mas、man分别为滚珠与丝杠、螺母接触椭圆的短半轴系数；E′为等效弹性模量；ρs、ρn分别为两个接触椭圆的主曲率；μ1、μ2分别为两个接触椭圆的有效泊松比；E1、E2分别为两个接触椭圆的有效弹性模量。

在轴向外载荷的作用下，垫片会产生相应的轴向位移和轴向变形，轴向位移量用xm表示，轴向变形量

(8)

(a)三维视图

其中，km为垫片的刚性系数，则垫片的位移量及变形量在法平面上的横向位移为(xm+δm)cosλ。由于倾覆力矩的存在，丝杠轴线与螺母轴线存在一定的偏角，故在沿着螺母轴线的不同横截面处，每颗滚珠的径向位移是不同的。滚珠的位置角表示如图3所示，在下面的讨论中均选定该情况下的径向位移为正值。假定第一颗滚珠的初始位置角为σ，相邻两颗滚珠球心的角度为φ，则任意一颗滚珠的位置角

ψi=(i-1)φ+σ

(9)

假设螺母中滚珠循环圈数为Z，丝杠的螺距为Lp，则φ=(2πZ)/N。ΔL为相邻两颗滚珠的轴向距离，则ΔL=ZLp/N。根据图3所示的几何位置关系，可以得到螺母A和螺母B中任意一颗滚珠的径向位移分别为

(10)

(11)

按照之前的假定，螺母滚道中心On视为在空间固定，则在轴向外载荷和倾覆力矩作用下，滚珠球心以及丝杠和螺母滚道曲率中心的几何位置变化如图4所示。其中，P点与Q点分别为轴向外载荷和倾覆力矩作用前滚珠与丝杠和螺母滚道的接触点，P′点和Q′点分别为轴向外载荷和倾覆力矩作用后滚珠与丝杠和螺母滚道的接触点，On、Os和Ob分别为轴向外载荷和倾覆力矩作用前的螺母滚道曲率中心、丝杠滚道曲率中心和滚珠球心，O′s和O′b分别为轴向外载荷和倾覆力矩作用后的丝杠滚道曲率中心和滚珠球心，βi为轴向外载荷和倾覆力矩作用后的接触角。

图4 滚珠与丝杠、螺母滚道曲率中心的位置关系变化图Fig.4 The positional relationship change diagram of thecurvature center of the ball, screw and nut raceway

丝杠在法平面的旋转角θ与在轴平面的旋转角θ′不同，根据空间几何关系，其相互转化关系为

tanθ=tanθ′cosλ

(12)

在滚珠没有受到外加轴向载荷和倾覆力矩的情况下，各滚珠接触点处丝杠滚道中心与螺母滚道中心的距离

M0=OnOs=rn+rs-2rb

(13)

式中，rn、rs、rb分别为螺母滚道曲率半径、丝杠滚道曲率半径和滚珠半径。

在螺母仅受预紧力的情况下，各滚珠接触点处丝杠滚道中心与螺母滚道中心的距离

M=M0+δi0

(14)

在轴向外载荷和倾覆力矩作用后，螺母A中各个滚珠接触点处丝杠滚道中心与螺母滚道中心的距离

(15)

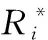
螺母A中各滚珠的接触变形

(16)

螺母A中各滚珠的接触角

(17)

同理，螺母B中各个滚珠接触点处丝杠滚道中心与螺母滚道中心的距离

(18)

螺母B中各滚珠的接触变形

(19)

螺母B中各滚珠的接触角

(20)

根据赫兹弹性接触理论，螺母A和螺母B中每颗滚珠法向接触载荷与变形量之间的关系为

(21)

(22)

当丝杠受到倾覆力矩时，相对于螺母轴线的力矩平衡方程为

(23)

联立式(1) 、式(17) 、式(21)、 式(23)，可以得到螺母A受到的力和力矩的平衡方程：

(24)

联立式(1) 、式(20) 、式(22) 、式(23)，得到螺母B受到的力与力矩的平衡方程：

(25)

螺母A与螺母B两者之间的力与力矩的平衡关系为

(26)

如图5所示，双螺母滚珠丝杠副的几何误差主要包括滚珠的尺寸误差、丝杠的导程误差以及丝杠和螺母滚道的齿形误差三种。由图5可知，丝杠导程误差可等效看成丝杠沿轴向产生变形，则螺母A和螺母B中每颗滚珠的变形量如下：

(27)

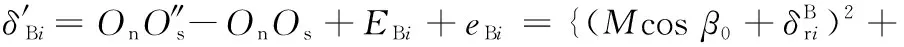
(28)

式中，EAi、EBi分别为螺母A和螺母B中任意滚珠的随机尺寸误差；eAi、eBi分别为螺母A和丝杠滚道以及螺母B和丝杠滚道的齿形误差；Es为丝杠的导程误差。

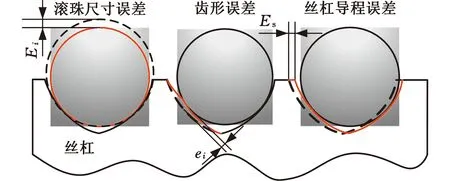
图5 三种几何误差下滚珠与滚道的位置关系图Fig.5 Position relationship diagram of ball andraceway under three geometric errors

螺母A和螺母B中每颗滚珠与滚道接触点处的接触角修正为

(29)

(30)

联立式(24)～ 式 (30)，得到几何误差和倾覆力矩作用下螺母A和螺母B受到的力和力矩平衡方程：

(31)

(32)

整个滚珠的受载模型可以通过MATLAB中牛顿迭代法工具箱计算得到，通过计算每颗滚珠的受力就可以分析出整个双螺母滚珠丝杠副的载荷分布情况。

2 实验验证

使用南京理工大学自主研发的轴向静刚度试验台测量双螺母滚珠丝杠副的轴向变形量，将测量结果与理论计算结果进行对比分析，以验证载荷分布模型的正确性。实验过程中采用“螺母固定”的测量方式，对滚珠丝杠旋转现象采取防转措施，并使用具有旋转补偿功能的新型滚珠丝杠副轴向静刚度测量装置，如图6所示。本实验选用的三个厂家生产的4010型滚珠丝杠副的相关参数值见表1，精度等级为3级，预紧方式为双螺母垫片预紧，动态摩擦力矩为(1.634±0.0817)N·m。

图6 滚珠丝杠副轴向静刚度测量装置Fig.6 Axial static stiffness measuring device of ball screw

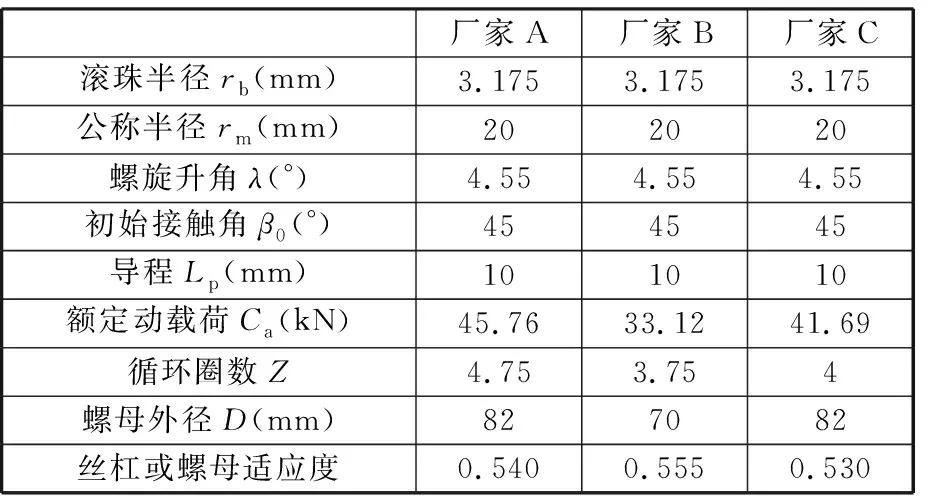
表1 CUT-2平台轴承参数表(实验)

移动横梁下方连接压力传感器，当丝杠受力时，压力传感器可以实时获取丝杠的受力情况，刚度测量装置中安装4个接触位移传感器(型号：Pretec 2940N，分辨力为 0.1 μm)记录滚珠丝杠副轴向变形量。实验前，以滚珠丝杠副额定动载荷Ca的30%为外加载荷，对滚珠丝杠副预压3次，消除测量装置之间的间隙。实验时，移动横梁以0.2 mm/min的速度对丝杠进行缓慢加载，外加载荷Fa达到0.3Ca(取整)后进行卸载，直到外加载荷为0。丝杠测量基准上，3个轴线方向的接触式位移传感器测得的丝杠轴向变形量分别为d1、d2、d3；旋转方向上，接触位移传感器测得的丝杠相对于螺母的旋转变形量为d4。滚珠丝杠副中丝杠与螺母间的相对变形量d=(d1+d2+d3)/3-Lpd4/(2πL)(L为测量旋转变形量的位移传感器接触点到丝杠轴线的距离)。

实验需重复测量3次以上(确保每根丝杠多次测量的数据重复性较好，如某次测量数据明显区别于其他各次测量数据，则视为异常，剔除该次测量数据，分析原因并重新补测)。为保证实验结果的准确性，设定预加载力为0.9 kN，当加载力不大于0.9 kN时，数据不参与轴向变形量计算。在施加载荷大于起始载荷而小于预设最大载荷的加载或卸载过程中，根据各传感器在各数据采集点的测量值相对于预加载时测量值的变动量，计算得到相对于预加载时的载荷及变形的变动量。以载荷增量为横坐标、相对变形量为纵坐标，绘制点图。利用MATLAB中牛顿迭代法工具箱计算该滚珠丝杠副在不同轴向外载荷作用下的轴向变形量，计算结果与实验结果对比如图7所示。

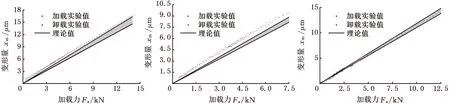
(a)厂家A (b)厂家B (c)厂家C图7 实验结果与理论结果对比Fig.7 Comparison of experimental results and theoretical results

由于所选滚珠丝杠副的精度等级为3级，滚珠精度等级为G10，故根据丝杠出厂设置参数表和ISO 3408-3，以及误差服从正态分布，可设定滚珠的随机尺寸误差为N(0，(0.5/6)2)，滚道的随机齿形误差为N(0，(4/6)2)，丝杠的导程误差为N(0，(2.5/6)2)。可以看出，由于不同滚珠尺寸误差和滚道齿形误差数据的随机性，最终得到的加载-变形曲线并不是一个固定值，而是在某一范围内波动的变化量，图7中用剖面线标示。厂家A、B、C轴向变形量的理论值与实验值的最大相对偏差分别为17%、18%和6%，原因是本文模型计算的是接触刚性，而实验结果包含了丝杠、螺母的变形以及扭转刚性等，故理论值会相对实验值偏小。由于实验设备和条件的限制，无法测量倾覆力矩,故本文建立的双螺母滚珠丝杠副载荷分布模型可在一定程度上有效计算滚珠的受力。

3 结果讨论

为了研究轴向外载荷、几何误差、倾覆力矩对双螺母滚珠丝杠副载荷分布的影响，本节选用陕西汉江机床有限公司生产的FN系列4010型滚珠丝杠副进行MATLAB仿真分析，滚珠丝杠副的具体相关参数见表2。该滚珠丝杠副的额定动载荷为30 kN，采用外循环方式，丝杠和螺母材料均为GCr15。在滚珠丝杠副的A、B两螺母中共有138颗滚珠，由于返向器中的12颗滚珠不受载，故A、B螺母中各有63颗滚珠受载。

表2 滚珠丝杠副参数表(仿真)

3.1 轴向外载荷对载荷分布的影响

当丝杠受到10 kN·mm的倾覆力矩时，双螺母滚珠丝杠副在不同轴向外载荷下的载荷分布如图8所示。可以看出，轴向外载荷从6 kN增加到20 kN时，滚珠丝杠副中滚珠受到的最大法向接触载荷由255.51 N增大到489.58 N，最小法向接触载荷由73.02 N减小到0，且丝杠副中最大与最小法向接触载荷的差值由182.49 N增大到489.58 N。由此可知，随着轴向外载荷的增加，螺母A中滚珠与滚道的法向接触载荷增大，螺母B中滚珠与滚道的法向接触载荷减小，且轴向外载荷的增加会导致螺母A和螺母B距离垫片相同位置处滚珠的受力差值变大。此现象的原因在于轴向外载荷的存在会增大螺母A受到的轴向载荷，使螺母A中滚珠受到的法向接触载荷相应增大，而轴向外载荷的存在会适当抵消螺母B受到的轴向载荷，使螺母B中滚珠受到的法向接触载荷相应减小。

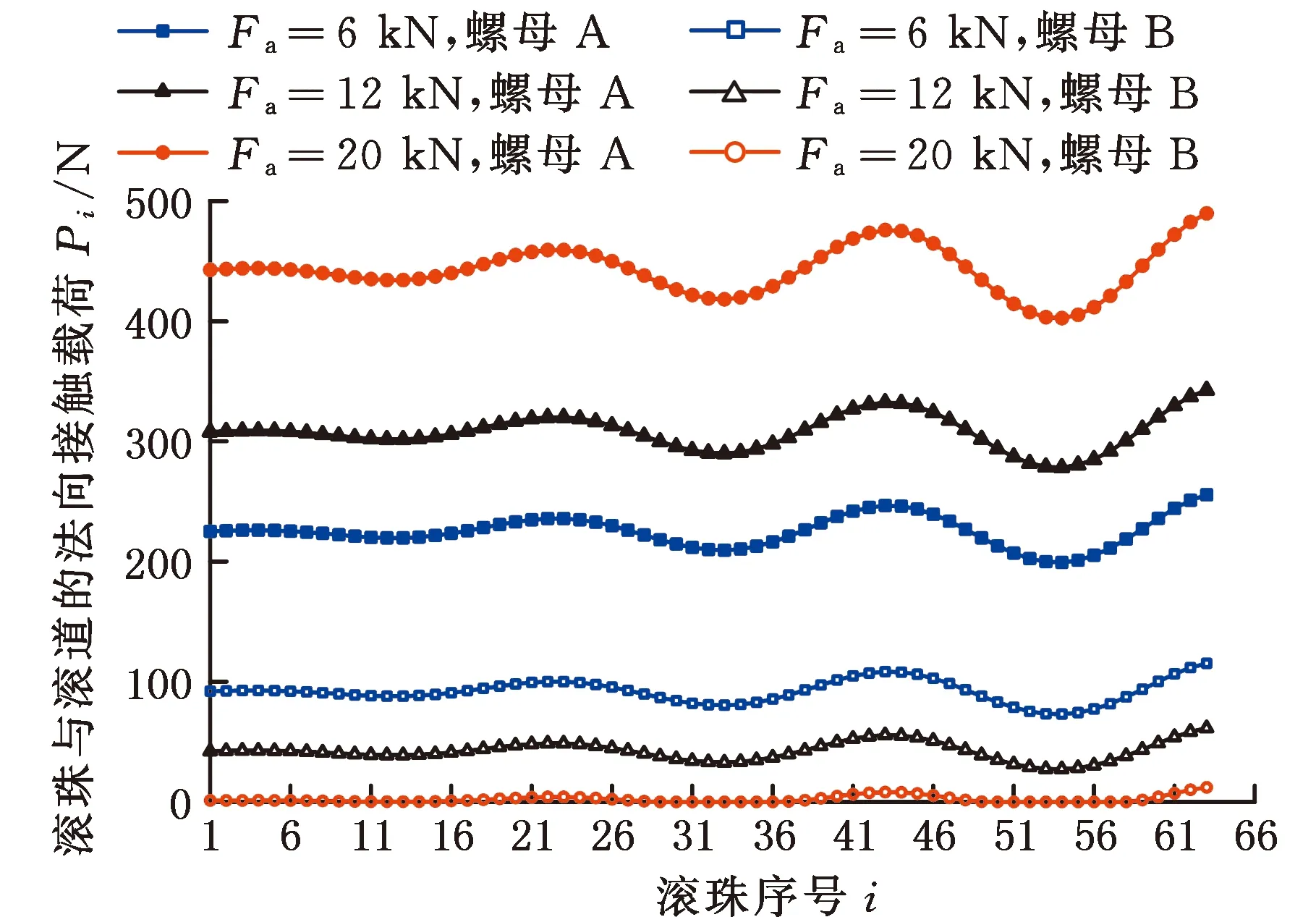
图8 不同轴向外载荷下双螺母滚珠丝杠副的载荷分布图Fig.8 Load distribution diagram of double nut ballscrew under different axial external loads

由MATLAB计算可知，当轴向外载荷增大到18.3 kN时，螺母B开始出现滚珠不受载现象，此时第54颗滚珠受到的法向接触载荷为0。当继续增加轴向外载荷至23.6 kN时，螺母B中的63颗滚珠正好全部不受载，此时滚珠与滚道完全脱开，形成卸载状态，造成滚珠丝杠副的失效。在这种状态下，滚珠与滚道之间的接触处于极其不稳定的状态，可能会导致滚珠丝杠副中的油膜破裂、滚珠与滚道之间的接触角改变，从而加剧磨损、降低寿命。由此推断，该双螺母滚珠丝杠副在10 kN·mm倾覆力矩的作用下，可以承受的最大工作载荷为23.6 kN。

3.2 倾覆力矩对载荷分布的影响

低载(轴向外载荷为6 kN)状态时双螺母滚珠丝杠副在不同倾覆力矩下的载荷分布如图9所示。可以看出，倾覆力矩的增加会导致滚珠丝杠副中93.65%的滚珠受到的法向接触载荷增大。在螺母A、B载荷分布曲线的第一个波谷处，第11～16颗滚珠的受载随着倾覆力矩的增加而增大；至第二个波谷处，第31～36颗滚珠的受载几乎不受倾覆力矩的影响；在最后一个波谷处，第52～55颗滚珠的受载随着倾覆力矩的增加而略微减小。选用一侧螺母的(Pi,max-Pi,min)/Pi,min来表征载荷分布曲线的波动幅度，则当倾覆力矩从10 kN·mm增加到30 kN·mm时，螺母A的波动幅度从28.18%增大到88.55%，螺母B的波动幅度从57.89%增大到186.53%。由此推断，倾覆力矩越大，螺母A、B中滚珠受到的法向接触载荷的波动幅度越大，相邻滚珠间的受载越不均匀,故在实际应用中，应尽量避免倾覆力矩的存在，否则会由于滚珠受力不均导致滚珠丝杠副的刚性降低，寿命缩短。

图9 不同倾覆力矩下双螺母滚珠丝杠副的载荷分布图Fig.9 Load distribution diagram of double nut ballscrew under different overturning moments

3.3 几何误差对载荷分布的影响

由图5可以看出，滚珠的尺寸误差与滚道的齿形误差对滚珠丝杠副载荷分布的影响规律相似，故在后文中仅分析以上两种误差之和对双螺母滚珠丝杠副载荷分布的影响。在双螺母滚珠丝杠副受到10 kN·mm的倾覆力矩(轴向外载荷为6 kN)的情况下，利用MATLAB随机产生误差范围分别为±1 μm和±2 μm的两组数据，绘制滚珠丝杠副的载荷分布如图10所示。由于误差数据的随机性，载荷分布曲线不再是平滑的曲线，而是呈现在一定范围内无规律上下波动的趋势，因此选用标准差来反映载荷分布的不均匀程度。当误差从±1 μm增大到±2 μm时，螺母A和螺母B中滚珠受载的标准差分别从25.02和18.57增大到42.13和31.27，且滚珠丝杠副的最大法向接触载荷与最小法向接触载荷的差值从209.70 N增大到了268.79 N。可以看出，由于误差的存在，每颗滚珠的尺寸不再相同，导致滚珠与滚道之间的接触载荷沿着无误差时的载荷分布曲线上下波动，且误差范围越大，波动幅值越大，载荷分布越不均匀。因此，选用高精度的滚珠可有效改善双螺母滚珠丝杠副中载荷分布不均的现象，降低磨损，延长使用寿命。

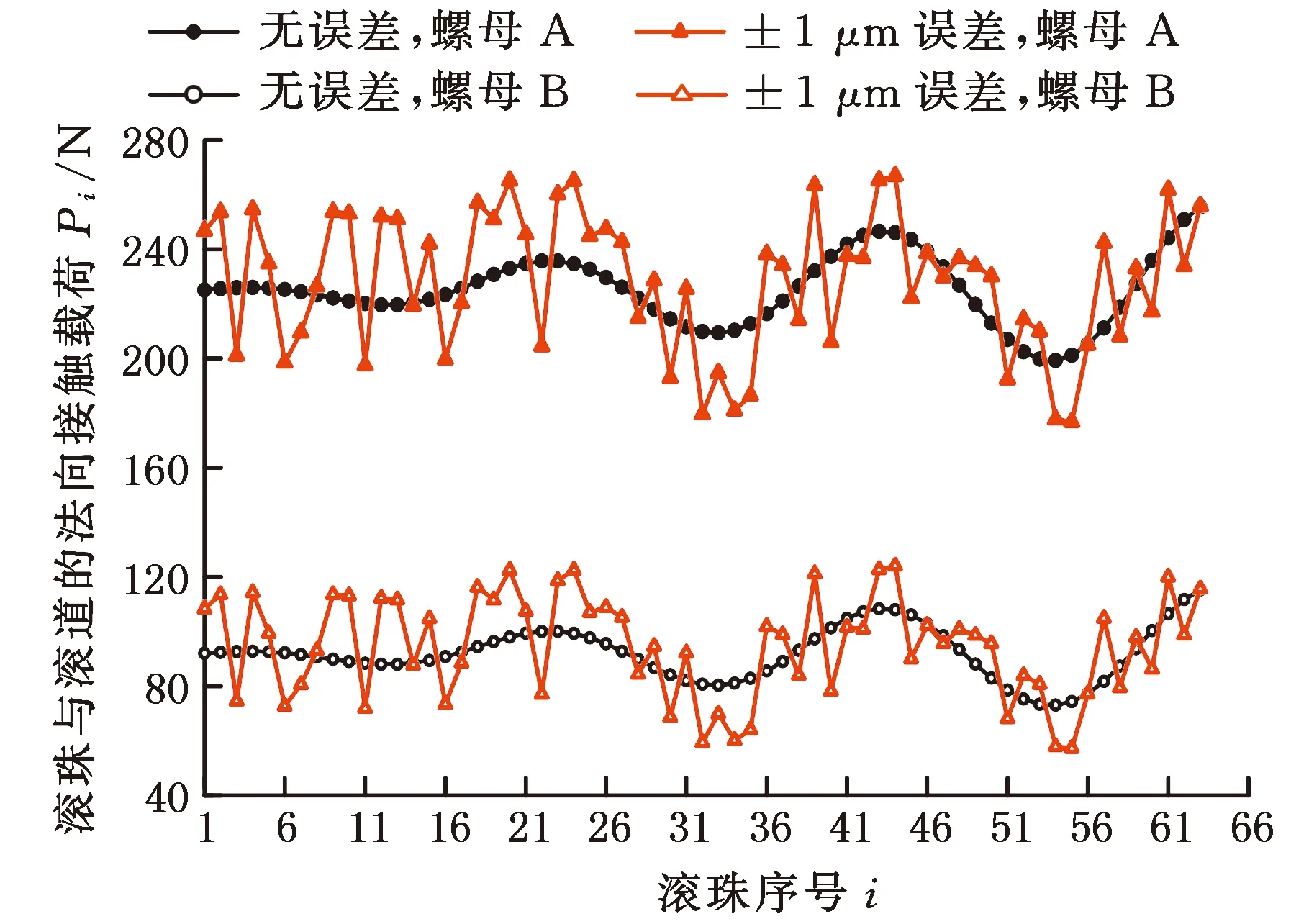
(a)±1 μm误差

与前面尺寸误差和齿形误差的条件相同，当双螺母滚珠丝杠副受到10 kN·mm的倾覆力矩(轴向外载荷为6 kN)时，丝杠导程在1 μm误差下的载荷分布如图11所示。该误差下滚珠丝杠副的最大法向接触载荷与无误差情况相比，从255.51 N增大到了280.97 N，最小法向接触载荷从70.02 N减小到了57.29 N。可以看出，丝杠导程误差使螺母A中滚珠与滚道的法向接触载荷增大，螺母B中滚珠与滚道的法向接触载荷减小，且螺母A、B距离垫片相同位置处滚珠的受力差值增大。

图11 丝杠导程误差下双螺母滚珠丝杠副的载荷分布图Fig.11 Load distribution diagram of double nut ballscrew under lead error of screw

三种误差分别作用和共同作用在双螺母滚珠丝杠副上的载荷分布如图12所示。从图12a中可以看出，在±1 μm尺寸误差和齿形误差的影响下，滚珠丝杠副的最大法向接触载荷与最小法向接触载荷之差为209.7 N；在±1 μm导程误差的影响下，滚珠丝杠副的最大法向接触载荷与最小法向接触载荷之差为223.68 N。因此，在滚珠丝杠副受载不均方面，误差大小相同时导程误差的影响大于尺寸误差和齿形误差。当分别考虑螺母A和螺母B滚珠的受载情况时，可以发现，螺母A中滚珠在导程误差下的受载普遍大于滚珠在尺寸误差和齿形误差下的受载，螺母B中滚珠在导程误差下的受载普遍小于滚珠在尺寸误差和齿形误差下的受载。图12b显示了三种误差共同作用在双螺母滚珠丝杠副上的载荷分布，可以看出，与无误差情况相比，此时滚珠丝杠副的最大法向接触载荷由255.51 N增大到了299.78 N，最小法向接触载荷由73.02N减小到42.83N，故±1 μm尺寸误差和齿形误差以及±1 μm导程误差的共同作用使滚珠丝杠副中滚珠的最大法向接触载荷与最小法向接触载荷的差值增大了40.80%。

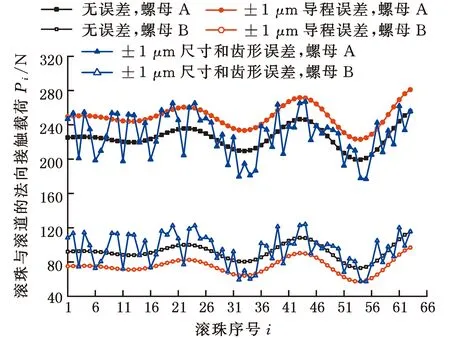
(a)三种误差分别作用

3.4 综合分析双螺母滚珠丝杠副的载荷分布

在轴向外载荷、几何误差和倾覆力矩的共同作用下，双螺母滚珠丝杠副的载荷分布三维图见图13和图14。图13为在低载(轴向外载荷为6 kN)、中载(轴向外载荷为12 kN)和重载(轴向外载荷为20 kN)下载荷随倾覆力矩变化三维图，此时导程误差为±1 μm，尺寸误差和齿形误差之和为±1 μm。可以看出，由于几何误差的存在，导致滚珠的载荷分布波动极大，在相同的轴向外载荷条件下，即使倾覆力矩从5 kN·mm增大到30 kN·mm，也仍有部分滚珠受到的法向接触载荷与在5 kN·mm倾覆力矩下部分滚珠受到的法向接触载荷相差不大,故几何误差对滚珠载荷分布的影响较大，会抵消部分倾覆力矩带来的影响。图14为在低载、中载和重载下载荷随几何误差变化三维图。此时导程误差为1 μm的定值，倾覆力矩为10 kN·mm。可以看出，滚珠尺寸误差和滚道齿形误差之和从±1 μm增大到±4 μm时，螺母B中部分滚珠受到的法向接触载荷显著增大或减小，在重载情况下更容易出现第一颗滚珠不受载、与滚道脱离的现象，但也可减缓螺母B中所有滚珠与滚道脱离，即卸载状态的发生。

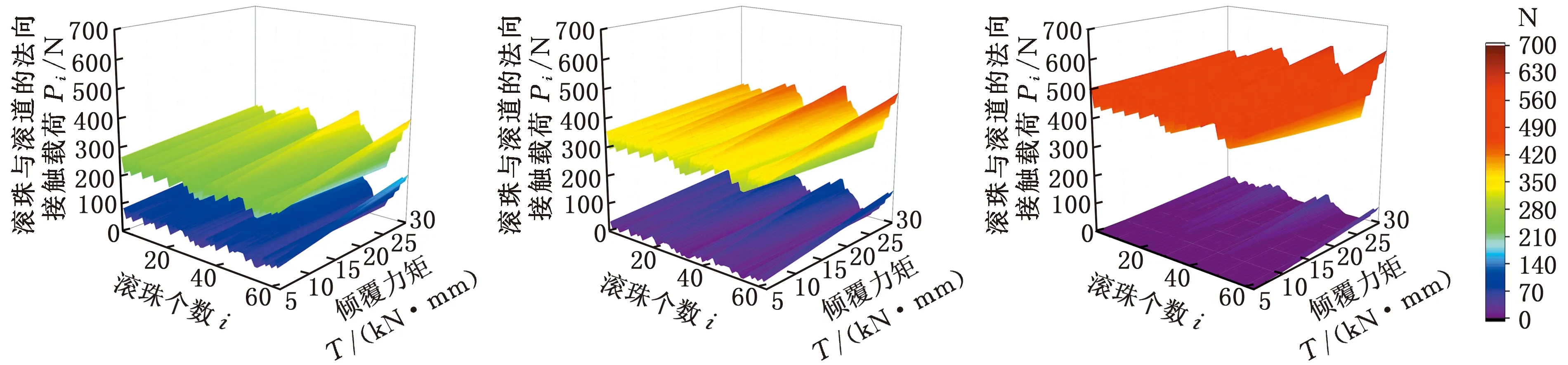
(a)低载 (b)中载 (c)重载图13 低载、中载和重载下载荷随倾覆力矩变化三维图Fig.13 The 3D diagram of the load with the overturning moment under low load, medium load and heavy load

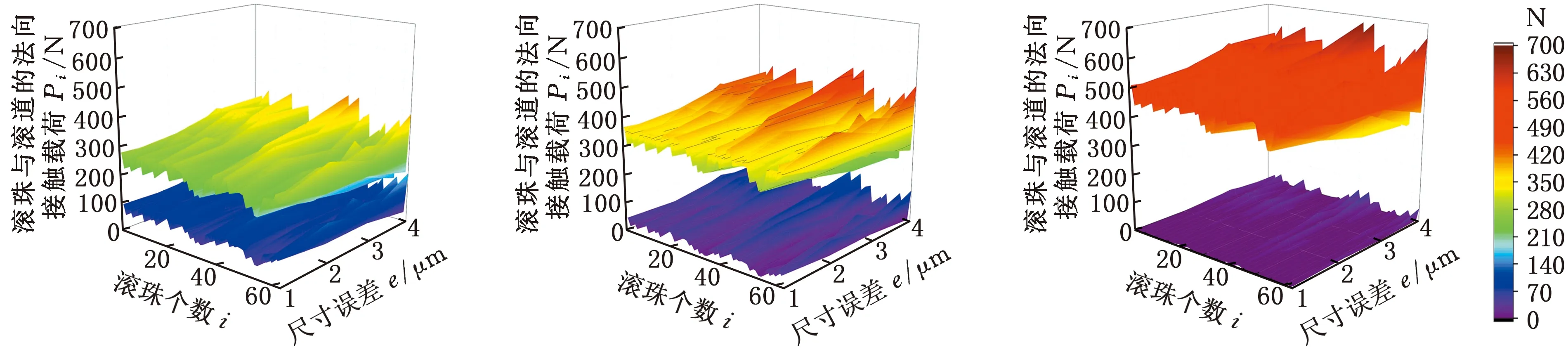
(a)低载 (b)中载 (c)重载图14 低载、中载和重载下载荷随几何误差变化三维图Fig.14 The 3D diagram of the load with geometric error under low load, medium load and heavy load

4 结论

(1)倾覆力矩一定时，增大轴向外载荷会使螺母A中滚珠受载增大，螺母B中滚珠受载减小，且会导致螺母A和螺母B距离垫片相同位置处滚珠的受力差值变大。当轴向外载荷增大到一定程度时，螺母B开始出现滚珠不受载现象，继续增大时，螺母B中所有滚珠与滚道完全脱开，形成卸载状态，造成滚珠丝杠副的失效。

(2)轴向外载荷一定时，倾覆力矩会导致双螺母滚珠丝杠副的载荷分布迅速变差，即载荷分布曲线的波动幅度变大。如本文使用的4010型滚珠丝杠副，当倾覆力矩从10 kN·mm增加到30 kN·mm时，螺母A和螺母B的载荷波动幅度分别增大60.37%和128.64%。因此在实际应用中，应尽量避免倾覆力矩的存在，否则会由于滚珠受力不均导致滚珠丝杠副的刚性降低，寿命缩短。

(3)轴向外载荷、倾覆力矩一定时，滚珠的尺寸误差和滚道的齿形误差会使滚珠与滚道之间的法向接触载荷沿着无误差时的载荷分布曲线上下波动，且误差范围越大，波动幅值越大，载荷分布越不均匀；丝杠的导程误差会使螺母A的受载增大，螺母B的受载减小。在误差大小一定的情况下，导程误差对载荷分布的影响程度大于尺寸误差和齿形误差，即双螺母滚珠丝杠副的载荷分布对导程误差的敏感程度更高。

(4)在轴向外载荷、几何误差和倾覆力矩的共同作用下，几何误差对滚珠载荷分布的影响较大，会抵消部分倾覆力矩带来的影响。滚珠尺寸误差增大时，螺母B中部分滚珠受到的法向接触载荷会显著增大或减小，在重载情况下更容易出现第一颗滚珠不受载、与滚道脱离的现象，但也可减缓螺母B中所有滚珠与滚道脱离，即卸载状态的发生。