基于振动台试验的空心桥墩地震易损性分析
申彦利,陈伟湖
(1.河北工程大学 土木工程学院,河北 邯郸 056038;2.河北省装配式结构工程技术研究中心,河北 邯郸 056038)
随着我国交通运输系统的高速发展,高大型桥梁等结构随之兴起。桥墩作为桥梁构件,对整个桥梁的安全与稳定起着重要作用。由于我国地震灾害多发,桥墩会受到不同程度的震损,因此,对桥墩损伤程度的有效评估至关重要。
易损性分析是指结构发生某种伤害或损坏的可能性,即结构在不同灾害等级下的失效概率,由易损性分析获得易损性曲线,从而较为准确地判断结构在不同地震动强度作用下发生某种损伤状态的超越概率,对结构的安全评估与修复具有重要意义。传统的基于桥墩破坏状态的易损性分析较缺乏实用价值,而基于性能的抗震设计成为桥墩损伤分析的发展趋势。牛荻涛[1]、孙颖[2]等对基于性能的结构易损性分析中,抗震性能水准的定义和划分进行了研究,为评估结构的损伤状态提供了划分依据。柳春光[3]等以墩顶漂移率作为损伤指标,以一连续桥梁作为算例,通过有限元软件建立数值模型,对其进行易损性分析。研究表明,易损性分析结果能够为灾害损伤估计提供参考。赵建锋[4]等基于墩顶位移损伤指标,利用ABAQUS软件建立数值模型,对圆柱形混凝土桥墩进行易损性分析,通过与已有研究成果的对比分析表明,易损性分析能够为桥墩震后安全评估提供一定依据。郑凯锋[5]等建立桥梁有限元模型,输入汶川地震实测地震波作用,以曲率延性为损伤指标对结构进行易损性分析,并进一步生成各构件的超越概率曲线,分别进行损伤评估。吴文朋[6]等基于有限元软件采用多种分析方法,对多跨钢筋混凝土连续梁桥进行非线性时程分析,通过结构超越概率曲线的对比分析,对各种分析方法的适用性和合理性进行了讨论。张超[7]等考虑高阶振型的影响,以弹塑性位移谱值为地震动强度参数,以位移作为损伤指标对钢筋混凝土矩形空心桥墩进行增量动力分析。PARK和ANG[8-9]基于大量混凝土梁柱试验统计结果,提出了考虑变形和结构累积塑性耗能的双参数地震损伤模型,为后续大量损伤模型的研究以及结构易损性分析提供了参考。
大多数基于性能的结构易损性分析,是建立在有限元模拟上,缺乏相关具体的地震响应数据或试验数据。本研究基于9个钢筋混凝土矩形空心桥墩的振动台试验,以及结合数值模拟试验,利用位移损伤指标对桥墩进行易损性分析,以实现对桥墩损伤状态的有效评估。
1 易损性地震需求模型
易损性分析通常以易损性曲线来表示结构在不同地震动强度作用下,发生失效的概率。假设地震需求参数服从正态分布,则相应的条件概率Pf表示为:
Pf=P[KD>KC|IM]=φ[ln(KD/KC)/λ]
(1)
(2)
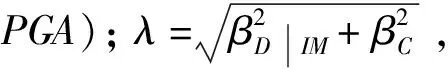
根据文献[10],假定地震需求参数KD与地震动强度参数IM存在指数关系,即:
KD=aIMb
(3)
式中:a和b为未知参数,可通过相应回归分析得到。
将等式(3)两边同时取对数得:
ln(KD)=ln(a)+bln(IM)
(4)
因此,将公式(4)代入公式(1)可得到:
Pf=φ[(ln(a)+bln(IM)-ln(KC))/λ]
(5)
2 损伤指标
基于性能的抗震设计,一般考虑将变形或能量作为指标参数。由于墩顶相对位移对桥墩的承载能力与损伤程度有较大的影响,因此,采用考虑墩顶相对位移的位移损伤指标对桥墩进行易损性分析。本研究定义无量纲位移损伤指标如下。
(6)
式中:Dd为位移损伤指标;d为桥墩墩顶最大相对位移响应;du为桥墩破坏位移。
为利用位移损伤指标对桥墩进行损伤评估,需要确定各个损伤状态对应的位移损伤指标限值范围。因此,本文利用有限元软件建立数值模型进行Pushover分析,以确定各个损伤指标限值点[2]。由于研究是基于9个空心桥墩试件的振动台试验,因此,分别建立了9个不同桥墩数值模型(M1-M9)进行单向推覆模拟,其中,桥墩模型的几何尺寸等参数与试验桥墩试件的参数一致。下面以M3桥墩模型为例(如图1示),由Pushover分析建立力-位移曲线(如图2示),确定各个指标限值点。其中屈服点是通过几何作图法确定的,破坏点取自极限荷载85%处的位置点。
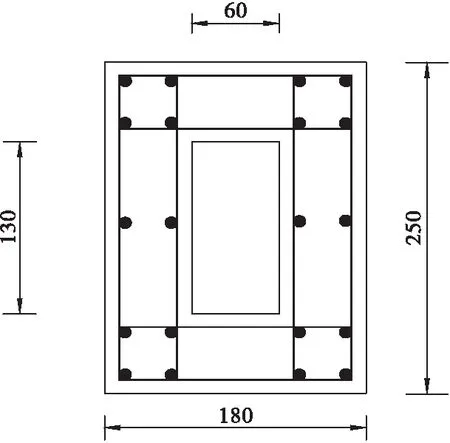
(a)截面尺寸
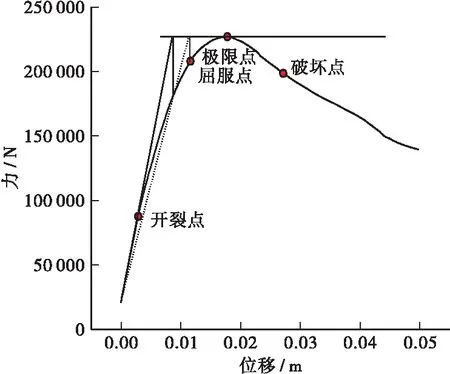
图2 力-位移曲线
由图2可确定各个指标限值点的位移值,同理可得到9个桥墩模型对应的各限值点的位移值,见表1。
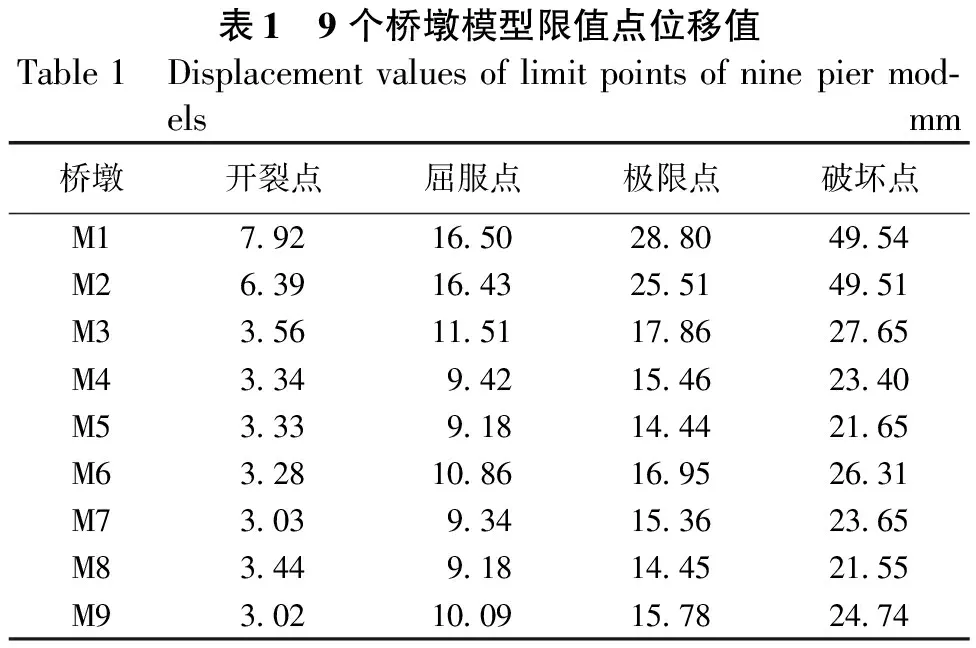
表1 9个桥墩模型限值点位移值Table1 Displacementvaluesoflimitpointsofninepiermod-elsmm桥墩开裂点屈服点极限点破坏点M17.9216.5028.8049.54M26.3916.4325.5149.51M33.5611.5117.8627.65M43.349.4215.4623.40M53.339.1814.4421.65M63.2810.8616.9526.31M73.039.3415.3623.65M83.449.1814.4521.55M93.0210.0915.7824.74
根据式(6)可确定各个Dd限值,即各限值点位移与破坏点位移的比值,由9个桥墩模型得到Dd限值,见表2。由表2可知,各指标限值不同,但大小基本相近,因此取其平均值。为确定具有较好普适性的量化指标Dd值,本文参考刘伯权[11]等、江近仁[12]等、牛荻涛[1]等在总结分析大量统计数据的基础上所提出的损伤指标限值范围(见表3),结合表2中的Dd限值的平均值,提出一组量化指标限值Dd值,见表4。
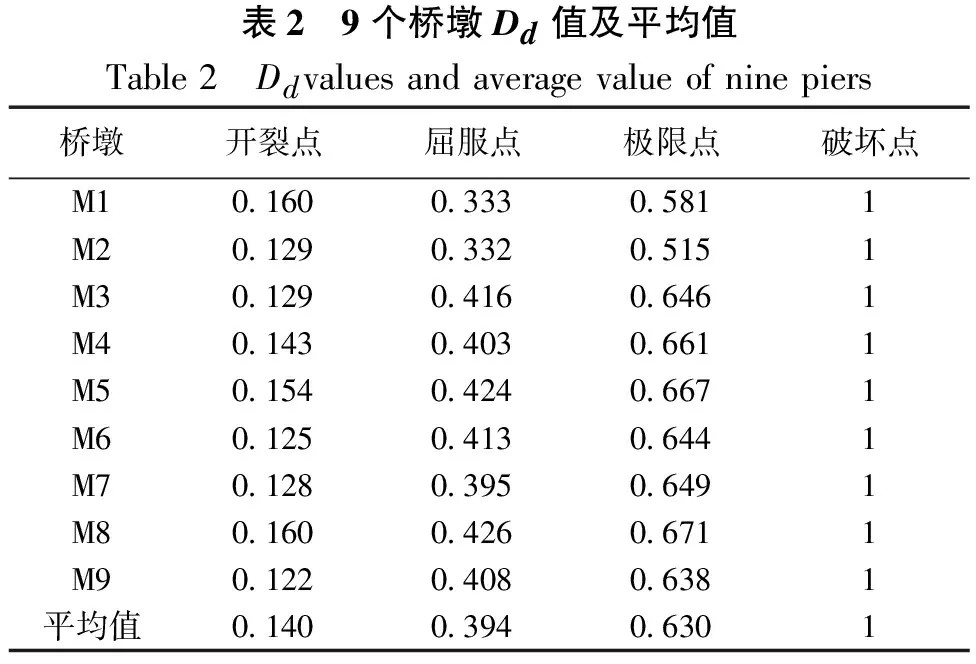
表2 9个桥墩Dd值及平均值Table2 Ddvaluesandaveragevalueofninepiers桥墩开裂点屈服点极限点破坏点M10.1600.3330.5811M20.1290.3320.5151M30.1290.4160.6461M40.1430.4030.6611M50.1540.4240.6671M60.1250.4130.6441M70.1280.3950.6491M80.1600.4260.6711M90.1220.4080.6381平均值0.1400.3940.6301

表3 已有研究的损伤指标范围Table3 Scopeofdamageindicatorsinexistingresearch已有研究基本完好轻微破坏中等破坏严重破坏倒塌刘伯权0~0.10.1~0.30.3~0.60.6~0.850.78~1江近仁0~0.2280.228~0.2540.254~0.420.42~0.780.78~1牛荻涛0~0.20.2~0.40.4~0.650.65~0.9 0.9~1

表4 各限值点对应的Dd值Table4 Ddvaluescorrespondingtoeachlimitpoint桥墩开裂点屈服点极限点破坏点Dd0.170.340.581
根据基于性能的结构抗震设计中,桥墩的性能水准与量化指标限值相对应,即指标限值将结构损伤划分成不同的性能标准。因此,根据表4中确定的各限值点Dd值,确定对应的性能水准,见表5。

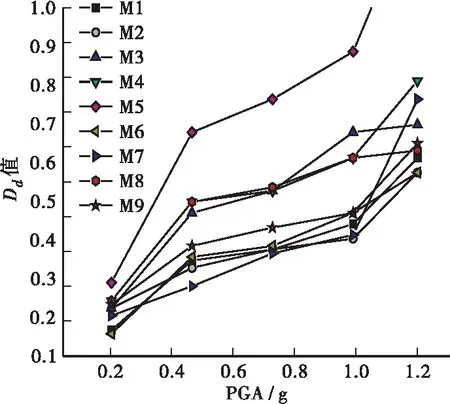
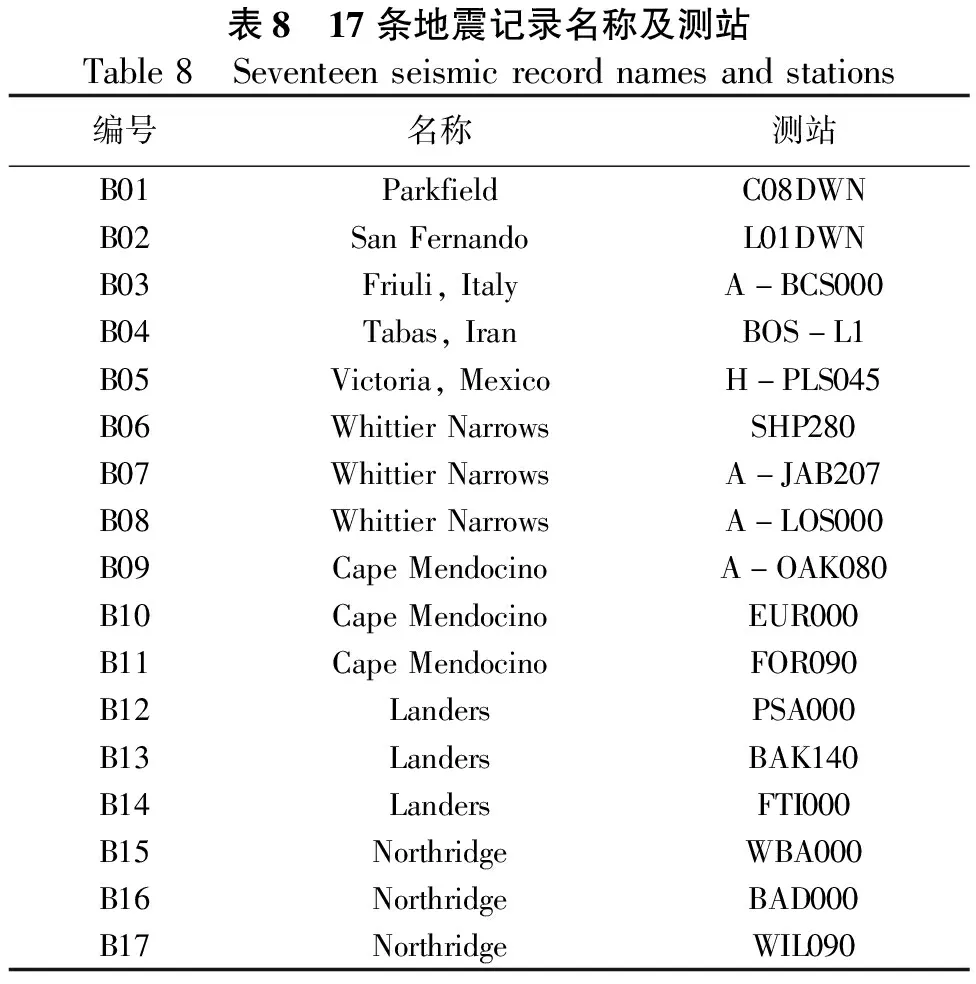
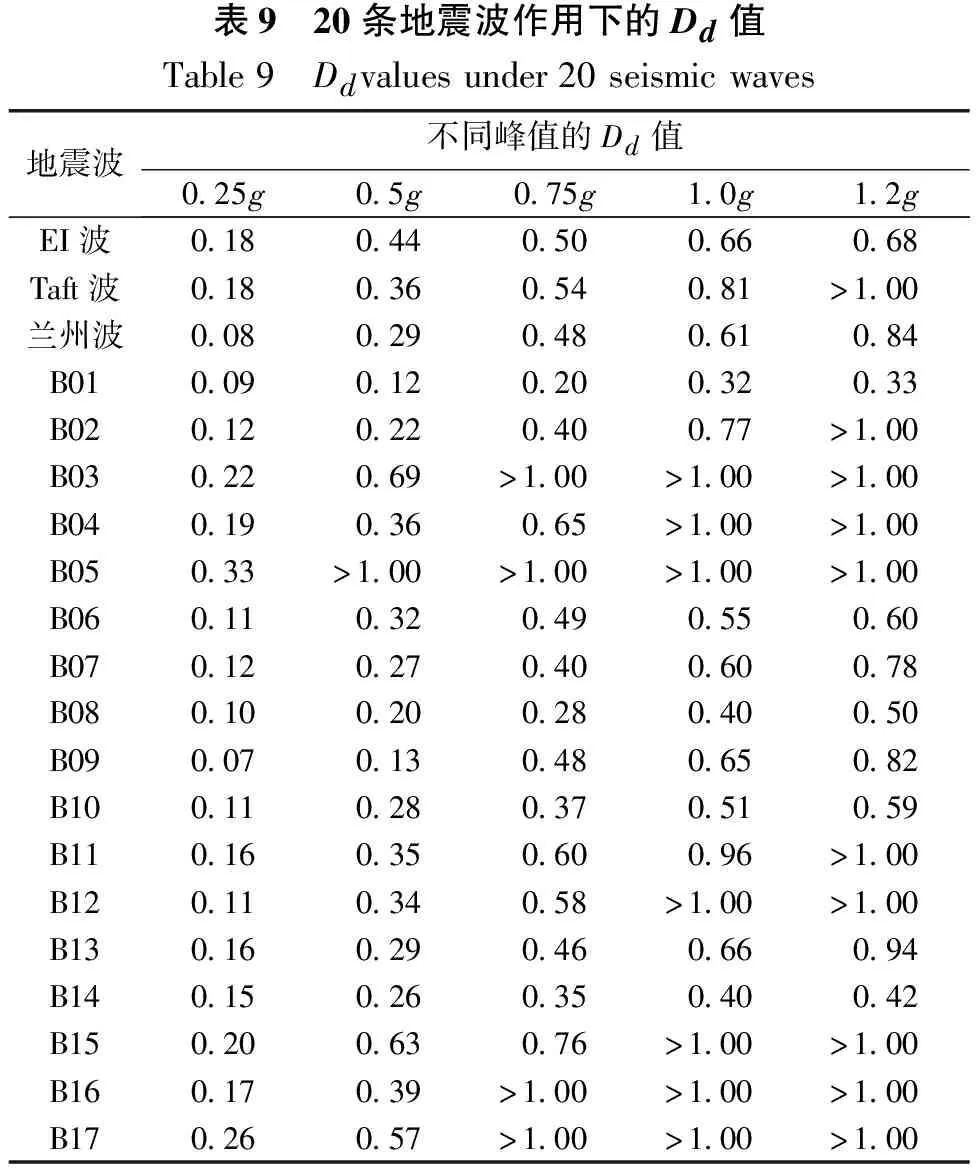
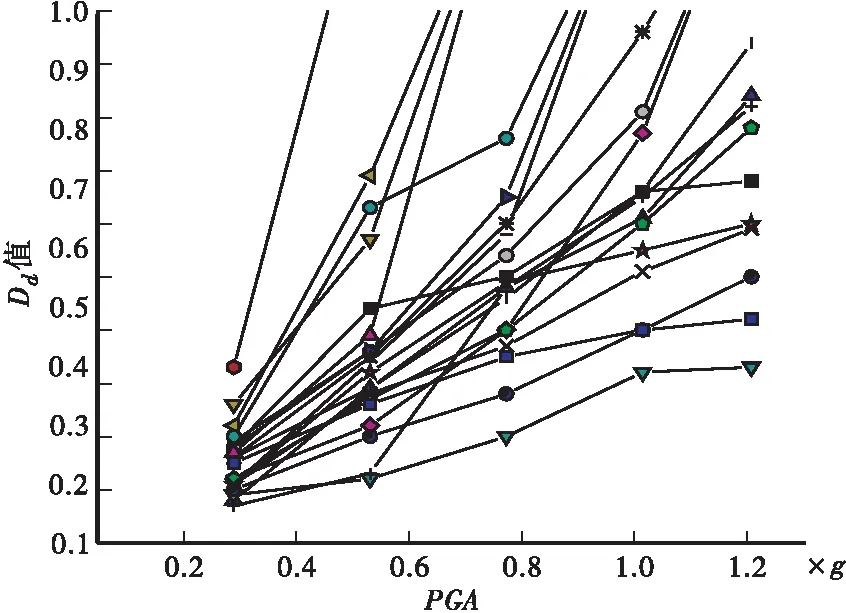
表5 性能水准定义划分Table5 Definitionanddivisionofperformancelevel性能水准水准描述量化指标水准1结构基本完好,不需修复仍可正常使用Dd≤0.17水准2稍微修复,可恢复正常使用0.17 本研究共针对9个钢筋混凝土矩形空心桥墩试件(试件编号为M1~M9)进行了振动台试验。桥墩试件与建立的9个桥墩模型一一对应。其中,桥墩截面外边缘尺寸为250 mm×180 mm,内侧空心边缘尺寸为130 mm×60 mm,混凝土保护层厚度为10 mm。核心混凝土和保护层混凝土等级均采用C40,钢筋采用HRB335等级[13]。桥墩试件其余参数见表6。试验中各采集装置的测点位置及桥墩试件模型如图3所示。 试验中将桥墩与振动台完全固定连接。用铁块代替上部承重荷载,容纳铁块的配重箱尺寸为1 m×1 m×0.7 m,通过改变铁块的数量调整桥墩的轴压比。 输入地震波选用EI Centro(EI)波、Taft波和兰州波,沿墩底长边方向单向输入。根据时间相似比,各地震波时间长度分别压缩为原波长的0.353倍。将各条地震波加速度调幅为0.25g、0.5g、0.75g、1.0g、1.2g共5种峰值,依次输入作用。 利用速度、加速度传感器及应变片等采集装置获取相应的地震响应数据,其中,各采集测点的位置布置如图3(a)所示。试验所获得的位移响应数据(见表7),利用式(6),计算各个桥墩在各地震峰值加速度作用下的Dd值,以此得到Dd值变化曲线如图4所示。 表6 桥墩试件参数Table6 Pierspecimenparameters试件墩高/mm轴压比纵向钢筋横向钢筋直径/mm配筋率/%直径/mm间距/mm体积配箍率/%M1144082.7450(双)4.0M2144082.74502.0M314400.182.73700.81M4144082.731300.44M5144061.531300.44M6144082.73700.81M714400.0582.731300.44M8144061.531300.44M9144061.53700.81 (a)测点位置 表7 9个桥墩试件的位移响应Table7 Displacementresponseofninepierspecimensmm试件EI波的位移Taft波的位移兰州波的位移0.25g0.5g0.75g1.0g1.2g0.25g0.5g0.75g1.0g1.2g0.25g0.5g0.75g1.0g1.2gM15.9715.2017.0020.3029.46.1813.1022.8028.029.33.1310.8013.7018.6025.7M28.8214.3016.7018.3027.26.2610.1016.6021.125.32.036.958.9311.2014.0M34.9812.2013.8018.2018.84.989.9514.9022.428.22.187.9913.1016.9023.1M44.5810.9011.7013.8018.86.077.6211.6015.738.31.726.418.4410.7015.4M55.4614.4016.2019.0023.35.2412.4018.7022.531.51.9311.4018.7027.7029.6M62.978.509.1911.6014.63.868.2612.7019.319.42.696.247.3910.9014.2M73.695.577.908.9817.82.964.977.5810.133.32.235.646.487.9911.8M84.3610.1011.1012.6013.24.548.8112.7018.419.01.949.3613.6015.0017.6M94.598.7010.0011.0015.65.408.3210.6012.714.82.024.506.118.5010.1 由图4所示,通过对9个空心桥墩的试验结果分析,在3种地震波作用下,Dd值随加速度峰值的增大,变化趋势基本一致。参照表5中各性能水准,9个桥墩试件在3种地震波作用下的Dd值,多集中在第3、第4水准范围内。 (a)EI波作用 图5为桥墩在不同地震波峰值加速度作用下的几种典型破坏情况。根据试验中桥墩的实际损伤情况,大部分桥墩试件在峰值加速度为0.5g时开始出现少量裂缝,随着峰值加速度增大,裂缝数量增多,出现贯通裂缝,并伴随着混凝土保护层的剥落,核心区未出现明显严重开裂,则桥墩的实际损伤状态大致处于前4个水准描述的范围之内。因此,实际损伤情况与Dd评估结果较为接近,说明Dd能够对桥墩损伤进行较为有效评估。 (a)EI波0.5g 为对桥墩进行增量动力分析,本研究以M3桥墩试件为例,基于振动台试验选用输入的3条地震波,另外引入17条地震记录(B01~B17)(见表8),进行数值模拟试验。 表8 17条地震记录名称及测站Table8 Seventeenseismicrecordnamesandstations编号名称测站B01ParkfieldC08DWNB02SanFernandoL01DWNB03Friuli,ItalyA-BCS000B04Tabas,IranBOS-L1B05Victoria,MexicoH-PLS045B06WhittierNarrowsSHP280B07WhittierNarrowsA-JAB207B08WhittierNarrowsA-LOS000B09CapeMendocinoA-OAK080B10CapeMendocinoEUR000B11CapeMendocinoFOR090B12LandersPSA000B13LandersBAK140B14LandersFTI000B15NorthridgeWBA000B16NorthridgeBAD000B17NorthridgeWIL090 由表8中17条地震记录及试验中的3条地震记录,共计20条地震记录作用。根据位移响应数据,代入公式(6)进一步得到各地震波峰值加速度作用下的Dd值,见表9。 表9 20条地震波作用下的Dd值Table9 Ddvaluesunder20seismicwaves地震波不同峰值的Dd值0.25g0.5g0.75g1.0g1.2gEI波0.180.440.500.660.68Taft波0.180.360.540.81>1.00兰州波0.080.290.480.610.84B010.090.120.200.320.33B020.120.220.400.77>1.00B030.220.69>1.00>1.00>1.00B040.190.360.65>1.00>1.00B050.33>1.00>1.00>1.00>1.00B060.110.320.490.550.60B070.120.270.400.600.78B080.100.200.280.400.50B090.070.130.480.650.82B100.110.280.370.510.59B110.160.350.600.96>1.00B120.110.340.58>1.00>1.00B130.160.290.460.660.94B140.150.260.350.400.42B150.200.630.76>1.00>1.00B160.170.39>1.00>1.00>1.00B170.260.57>1.00>1.00>1.00 根据表9中桥墩试件在20条地震波各峰值加速度作用下的Dd值,对各水准范围内Dd值的分布情况进行统计,如图6所示。 由图6可以看出,随着峰值加速度的变化,桥墩试件Dd值分布情况也随之改变,当峰值加速度为0.5g~1.0g时,指标值主要分布在第2、3、4水准范围内,当峰值加速度为1.2g时,指标值集中分布在第4、5水准范围内。 (a)0.25g作用下 图7为增量动力分析中Dd值与20条地震波不同峰值加速度之间的变化关系图。 图7 Dd值变化图 根据易损性地震需求模型,损伤指标Dd即对应式(1)中地震需求参数KD。由于假定地震需求参数与地震动强度之间存在指数关系,进而转化为式(4)中对数关系,因此,根据上文中获得的Dd值(见表9),可得到具体的回归方程如下: ln(Dd)=-0.372+1.104 ln(PGA) (7) 因此,将式(7)代入式(5)得: (8) 由此,根据正态分布概率求解式(2)可确定相应的超越概率值Pf,进而确定易损性曲线如下: 由超越概率曲线(图8)可知,当PGA在0.5g时,结构处于水准2状态的概率约为90%,处于水准3状态的概率接近50%,而处于水准4和水准5状态的概率较低;当PGA为1.0g时,结构处于水准2状态和水准3状态的概率约为100%,处于水准4状态的概率为70%左右,而处于水准5状态的概率不足20%。由此,通过超越概率曲线可直观的判断出结构在某一PGA作用下处于某种破坏状态的概率,从而实现对桥墩的易损性分析。 图8 超越概率曲线 本研究基于钢筋混凝土空心桥墩的振动台试验结果,结合数值模拟分析,利用位移损伤指标对桥墩进行易损性分析,得到以下结论: a.基于振动台试验结果,位移损伤指标能够实现对空心桥墩较为准确的损伤评估。 b.通过易损性曲线,能够对桥墩发生某种损伤状态的概率作出直观的判断。 c.可进一步采用试验与模拟相结合的方法,以及对损伤指标的计算方式进行改进,从而更好地对钢筋混凝土空心桥墩进行易损性分析。3 试验验证
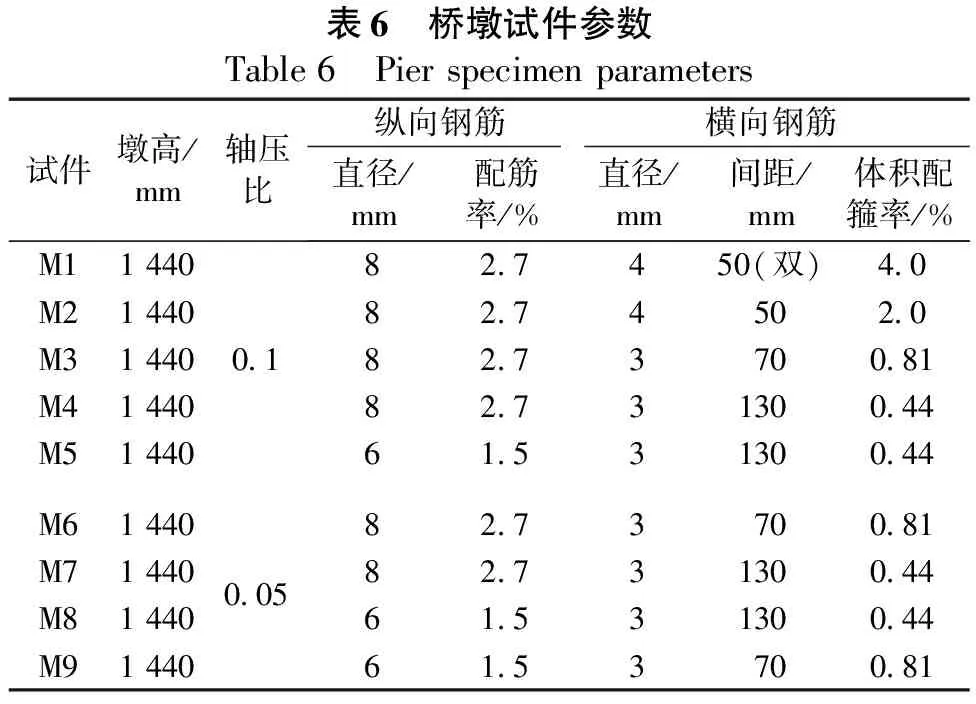
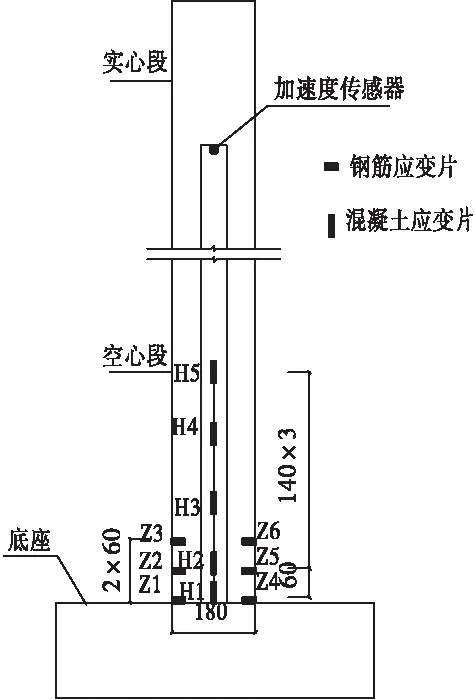
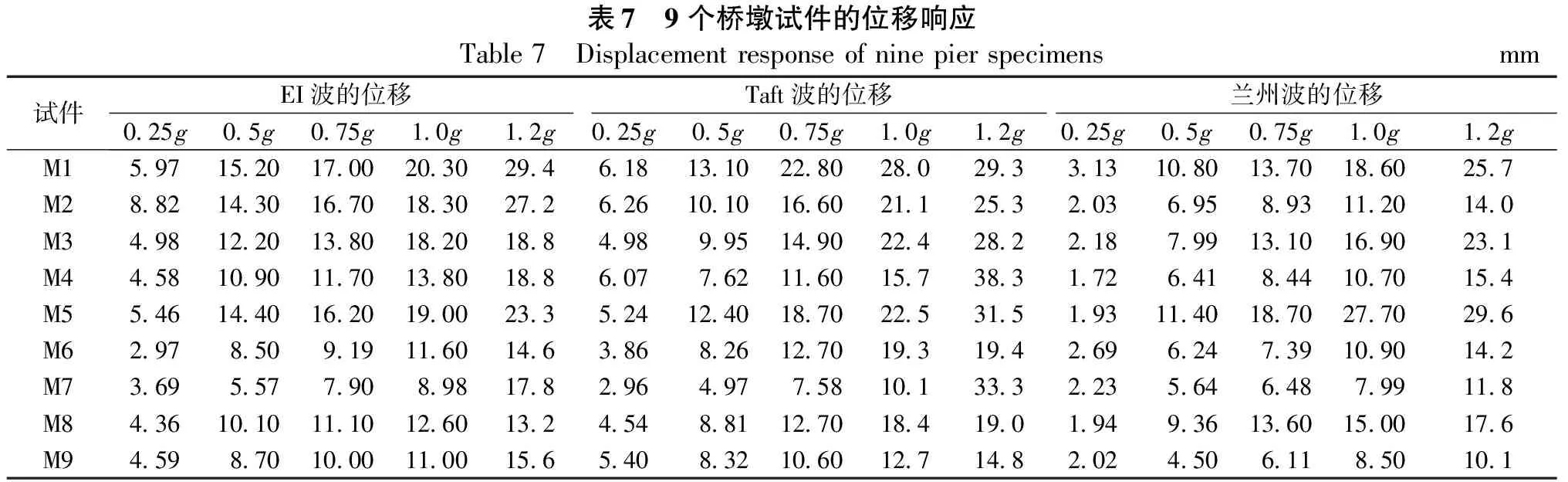

4 易损性分析
4.1 地震记录
4.2 Dd值及其分布

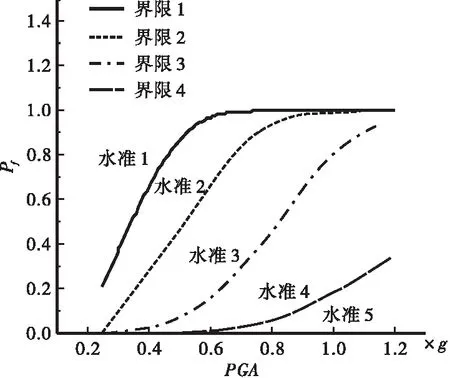
4.3 易损性曲线
5 结论

