求解一类非凸非光滑约束优化问题的邻近滤子束算法
王 晓 亮, 吴 奇, 田 玉 铢, 庞 丽 萍
( 大连理工大学 数学科学学院, 辽宁 大连 116024 )
0 引 言
考虑下面的约束问题:
其中目标函数f:Rn→R是局部lower-c2的,约束函数hi:Rn→R,i=1,2,…,m是凸的,但目标函数与约束函数都不必是可微的.注意到上面的问题可以转化为只包含一个约束的问题,具体地:若定义h(x)=max{hi(x),i=1,2,…,m},则原问题转化为
显然,函数h(x)也是定义在Rn上的凸函数.接下来,本文致力于该问题的求解.
滤子类方法(filter type methods)是求解约束问题的一类十分有效的方法[1-4],它经常涉及Pareto-domination准则,即:xdominatesy当且仅当f(y)≥f(x)和h+(y)≥h+(x),其中h+(x)=max{h(x),0}.滤子算法中,一个候选点可以作为新的下降步的前提是这个点不能被先前的迭代点所支撑(domination).这表明新的迭代点会获得下降的目标函数值或者较小的约束违反度(即较小的h+(x)值).
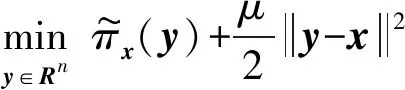
文献[4]采取了滤子策略和邻近束算法结合的思想来求解凸规划问题.本文将上述方法拓展来求解非凸非光滑问题.具体地,首先将凸化技术作用于目标函数,以增强目标函数的凸性;再利用改进函数算法将新获得的约束问题转化为无约束问题,同时采用邻近束算法技术和滤子策略对无约束问题进行求解.文献[7]中,针对一类非凸非光滑约束问题,作者提出了一种邻近滤子束算法.虽然算法近似,但存在着一些不同.具体的,与文献[7]相比,本文中改进函数的建立、相应切平面模型的构造和滤子策略的选取是不同的.
1 算法基础

假设1给定初始点x0和一个正参数M0,水平集T0满足
T0∶={x∈Rn:f(x)≤f(x0)+M0}⊆O
其中O是一个有界开集.
假设2假设Slater约束规范成立,即存在x∈Rn,使得h(x)<0成立.

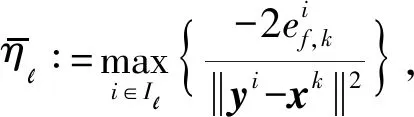
(1)
其中Il⊆{0,1,…,l}是束的指标集.下面建立一个增广的函数ψl(y):

(2)
(3)
由Φl(y)的定义可知问题(3)有唯一的解.束方法中常常涉及预测下降量,它的定义为
(4)
由yl+1的定义可得δl+1≥0.
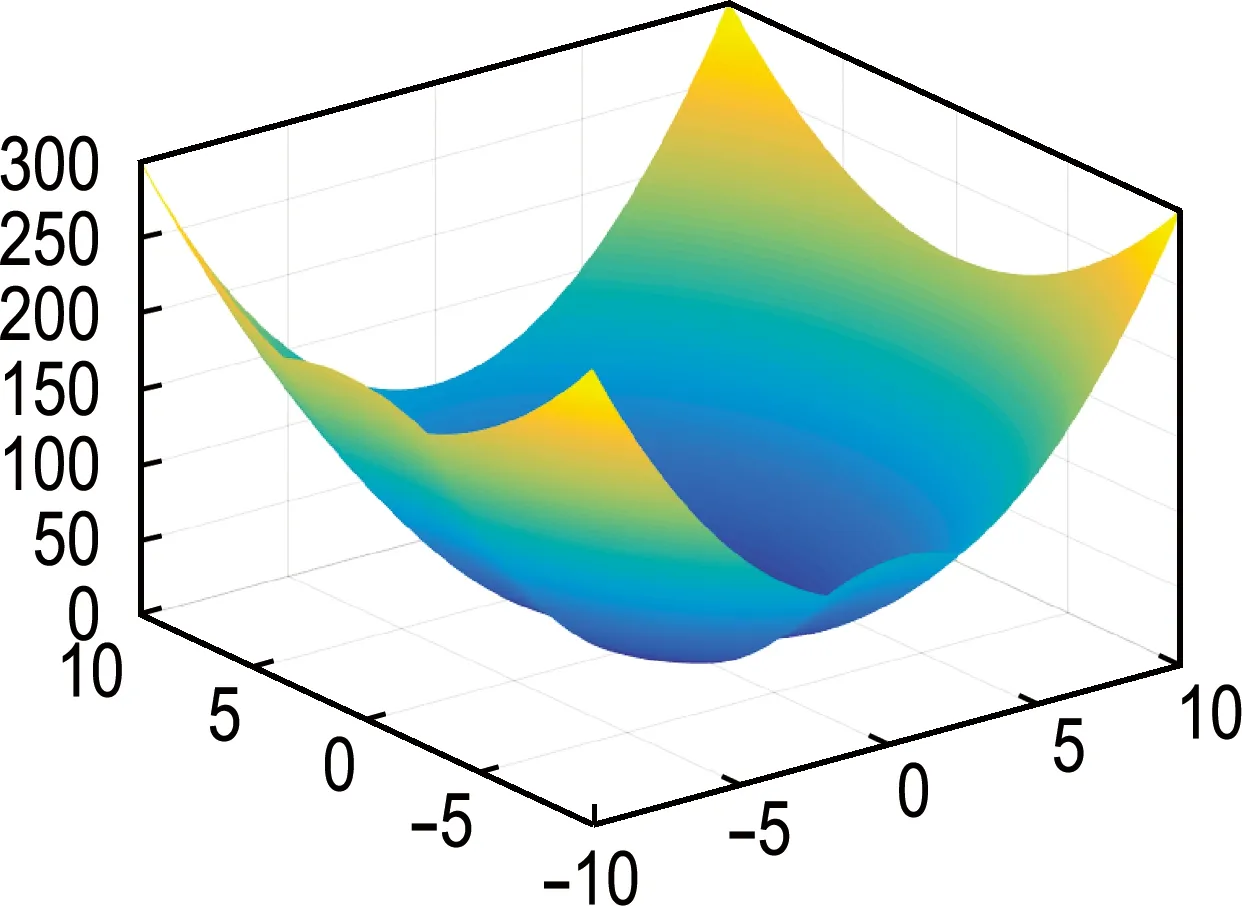
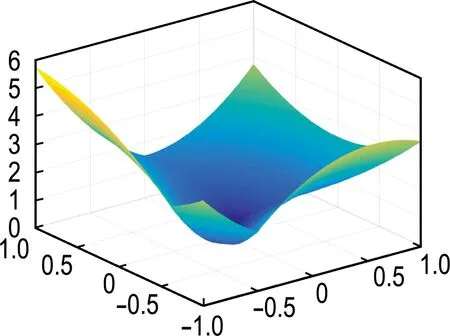
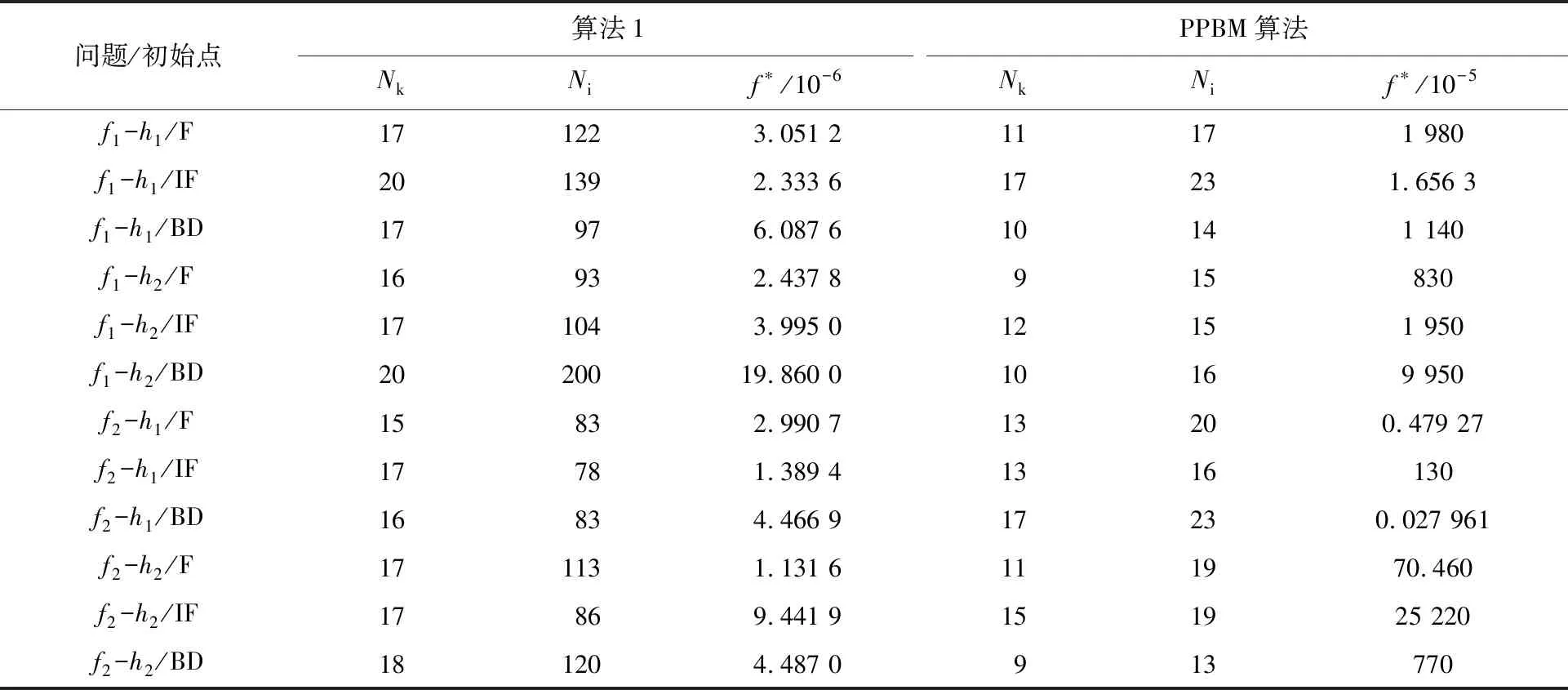
下面介绍本文所采用的滤子技术,可参见文献[4].首先给定两个参数γf,γh∈(0,1).这里将利用这两个参数来定义当前禁止域(forbidden region)、滤子(filter)和当前临时点对(temporary pair).具体地,在当前的下降指标k,滤子Hk由下面的点对构成,其中xi(i (5) 定义当前临时点对: (6) 算法1求解非凸非光滑约束问题的邻近滤子束算法. (7) 定义当前的禁止域: (8) 步骤2(模型产生与QP子问题).已知当前的稳定中心xk,当前的束信息Bl,参数μl和ηl.由式(2)计算当前的逐点切平面模型Φl(y).求解问题(3)来获得新的试探点yl+1,由式(4)来计算δl+1. 步骤3(停止准则).若δl+1≤T,则停止. 步骤4(邻近参数的更新).若πl(yl+1)>πl(xk)+M0,称这个增长是不可接受的,并更新邻近参数μl=Γμμl返回步骤2,否则置μl+1=μl. h+(xk)≤m1δl+1; (9) 则称yl+1为新的稳定中心,并转至凸化参数更新步;否则,转下一步. 步骤6(下降测试).若条件 πl(yl+1)≤πl(xk)-ζδl+1 (10) 成立,则转至恢复步,否则为零步(null step). 步骤7(恢复步).计算yl+1使得 (11) 称yl+1为新的稳定中心. 步骤8(凸化参数的更新).应用下面的准则来更新凸化参数η: (12) Lower-c2函数都是局部Lipschitz连续的.由T0是紧的,因此函数f和h在集T0上都是全局Lipschitz连续的.由πl(·)的定义,可知πl(·) 在集T0上也是Lipschitz连续的并记相应的Lipschitz常数为L. 引理1(邻近参数稳定性).迭代点序列{yl}由算法1产生,当前下降点xk在束信息中且它对应的迭代指标为lk,即xk=ylk.则在算法的步骤2和步骤4之间只有有限多次循环. □ □ 引理3对于算法1,下面的关系成立: (i)给定k,若产生新的下降点xk+1,则下面两个条件至少一个成立: h+(xk+1)<γhh+(xk) ψl(xk+1)<ψl(xk)-γfh+(xk) (v)任意给定i∈N,若存在参数p≥1,使得xi+p为下降点,则xi+p∉Hi+1成立. 证明可参见文献[4]中命题1的证明过程,这里略去其证明. □ 接下来证明算法是合理的.在此之前,下降测试条件(10)等价于下面两个式子的组合,即 ψl(yl+1)-f(xk)≤h+(xk)-ζδl+1 (13) 与 h(yl+1)≤h+(xk)-ζδl+1 (14) 引理4算法1是合理的. 证明类似于文献[4]中命题2的证明过程,由引理1~3可得出结论成立. □ 下面给出算法1的全局收敛性分析.束方法产生的迭代点分为两类:下降步和零步.依据下降点是否无限,收敛性证明分为两部分.首先给出产生有限个下降点的情形. 证明相似的证明参见文献[4]中的定理4.1 与文献[11]中的引理2.2. □ 证明若xk不是问题的解,则由文献[6]中的定理4.5可得下降条件(10)在有限多零步后将得到满足,除非步骤5中的滤子测试首先得到满足(注意到在下降条件满足前,算法不进入恢复步).若滤子测试首先满足,则产生新的下降点.若下降条件首先得到满足,则由引理4可知,下降条件比滤子测试早满足的前提是xk是不可行点.这种情形下,将进入恢复步.引理4表明这种情形下也将产生新的下降点.因此综上所述,若xk为当前的下降步但不是问题的解,则算法1将产生新的下降点xk+1. □ 下面本文用两个引理分两种情形讨论有无限多下降步的情况.一种是下降步的极限点为可行点,另一种是下降步的极限点为不可行点.它们的证明可参见文献[4]中的命题4和5. ψl(ki)(xki)-ψl(ki+1)(xki+1)≥ζξ/2 (15) 特别地,对所有i≥i0的迭代都是ψ迭代. 接下来,假设下降步点列中仅有有限步对应着h+迭代,即存在一个指标k0使得对所有的k≥k0的下降步都对应着ψ迭代,因此序列{ψl(k)(xk)}k≥k0是单调递减的.下降步是有界的,从而有下面的极限式成立: ψl(k)(xk)-ψl(k+1)(xk+1)→0 (16) □ 本文测试算法1的数值表现并与文献[12]中的算法(简记为PPBM算法)进行比较.PPBM算法是利用惩罚函数策略结合邻近束方法来求解非凸非光滑约束问题.所有的测试都是在设备为2.10 GHz CPU和16 GB RAM的电脑上进行的.二次规划求解器采用的是MATLAB R2016b中的Quadprog.m. 图1 目标函数f1(x)图 图2 目标函数f2(x)图 0.5 0.5 0.5)为可行点(F);点x0=(1 -1 1 -1)为边界点(BD);点x0=(10 -10 10 -10)为不可行点(IF). 算法1的参数设置如下:m1=0.1,m2=0.5,ζ=0.05,γf=0.000 1,γh=0.999 9,μ0=2,η0=0,Γμ=2,Γη=0,M0=5,T=10-5.PPBM算法的参数采用文献[12]中默认的但置T=10-5.详细的数值结果见表1,其中问题表示约束问题的组成,如f1-h1表示目标函数为f1(x),约束函数为h1(x);初始点表示选取的初始点的各种类型,即可行点、不可行点与边界点;Nk表示下降步的次数;Ni表示迭代的次数;f*表示算法最终获得的函数值.数值实验表明算法1能够得到更精确的函数值,表明了算法的有效性. 表1 数值结果 本文研究了一类特殊的非凸非光滑约束优化问题,这类问题在很多重要领域都有广泛的应用.设计算法时,首先利用凸化技术对非凸的目标函数进行凸化,接着利用改进函数将修正的约束优化转化为无约束问题,最后利用邻近束算法来处理无约束优化问题.本文还分析了算法的合理性和收敛性.在数值实验部分,考虑了4个约束优化问题和每个问题涉及3个不同的初始点(可行点、不可行点、边界点).通过与相应算法的比较,可以得出针对上面的问题,本文的算法会得到更精确的函数值,从而验证了算法的有效性.

2 算法及其特性
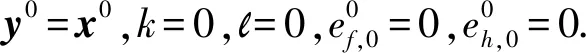




ψl(yl+1)≤ψl(xk)+h+(xk)-m2δl+1
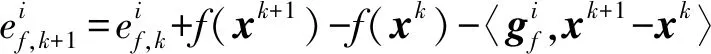
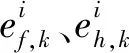

3 算法分析

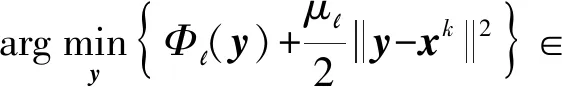
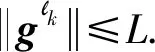



4 收敛性分析







5 数值实验
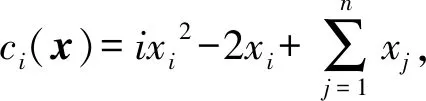
6 结 语

