基于BP神经网络的FRP筋与混凝土界面黏结强度预测

陈 健， 黄 丽 华， 曲 激 婷

( 大连理工大学 建设工程学部, 辽宁 大连 116024 )

0 引 言

纤维增强复合材料(fiber reinforced polymer，FRP)具有轻质高强、耐腐蚀、低磁性、抗疲劳等性能特点，在环境复杂的土木工程中使用具备得天独厚的优势，无论是现役结构的加固补强，还是直接作为混凝土中的受力构件，FRP筋已越来越多地用于工程实际中[1-2]．FRP筋与混凝土之间的黏结性能是影响FRP筋与混凝土结构的承载、变形和失效形式的关键因素．与传统钢筋的材料构成和加工方式不同，FRP筋属于正交各向异性材料，弹性模量低，抗剪性能差，通常采用多种表面设计和处理来提高界面黏结性能．近年来，针对FRP筋与混凝土界面的黏结性能，国内外学者提出了多个界面黏结滑移本构模型[3-6]．由于FRP筋与混凝土之间的黏结性能受FRP筋类型、表面形式、FRP筋直径、锚固长度、破坏模式、混凝土抗压强度和归一化的混凝土保护层厚度等多种因素的影响[7-10]，已有模型的适用性和计算精度均有较大局限性．

随着现代信息技术的飞速发展，大数据、人工智能等数据分析和识别技术越来越广泛地用于解决基础科学问题．近年来，人工神经网络(artificial neural network，ANN)和遗传规划(genetic programming，GP)等智能识别方法已应用于分析FRP筋与混凝土的界面力学性能问题[11-15]．Dahou等[16]收集了带肋钢筋拉拔试验数据，基于ANN模型预测界面黏结强度．Golafshani等[17]在2012年建立了ANN和模糊逻辑(FL)模型，整理了179组数据对混凝土与钢筋的黏结强度进行预测．在2015年，Golafshani等[18]研究了159组试验数据，包括缺口、铰接、拼接和倒置铰梁样本，利用ANN和GP预测了玻璃纤维(GFRP)增强混凝土的极限黏结强度，该人工神经网络和GP模型比多元线性回归模型更能准确地预测FRP筋与混凝土的黏结强度，并给出了规范方程．

本文将ANN技术用于预测多种FRP筋与混凝土界面的黏结性能．通过收集并处理国内外文献中292组相关试验数据，建立FRP筋混凝土拉拔试验数据库，以FRP筋类型、表面形式、FRP筋直径(d)、锚固长度(l)、破坏模式、混凝土抗压强度(f)和归一化的混凝土保护层厚度(c/d)为输入变量，以界面黏结强度为输出变量，建立界面黏结强度预测模型，通过数据库中的试验数据对网络模型进行训练，以实现对FRP筋与混凝土界面黏结强度的合理预测．

1 BP神经网络模型

ANN是基于生物学中神经网络的基本原理，在理解和抽象人脑结构与外界刺激响应机制后，以网络拓扑为理论基础，模拟人脑的神经系统对复杂信息的处理机制而建立的数学模型[18]．基于大量已有数据，使用数学训练过程学习输入和输出数据之间的关系，控制最小误差，实现未知结果预测．该方法的基本元素是称为感知器的人工神经元(neuron)，数学模型如图1所示，表达式如式(1)、(2)[19]所示．

(1)

(2)

式(1)为输入分量xi的加权和表达式．其中xi(i=1，2，…，n)是第i个神经元的输入值，wij为第i个神经元与第j个神经元的连接权值，b为神经元的阈值．式(2)为输出y的计算式，其中F为激活函数，一般采用sigmoid函数．

典型的多层前馈神经网络一般包含3层或3层以上，分别是输入层、一个或多个隐藏层和输出层．信息通过输入层从外部环境接收，并通过初始隐藏层传递给神经元，神经元之间的信息流由权值和阈值调节．一旦算出该神经网络的输出值，便进行训练，以优化网络的权值和偏差．

在目前已有的几种训练算法中，误差反向传播(back propagation，BP)算法通常能够给出令人满意的结果．BP算法是一种梯度下降算法，可根据误差函数的负值不断调整网络中的权值和阈值，直到将网络错误降至最低为止．更新后的权值和阈值分别由式(3)、(4)表示[16，19]．

(3)

(4)

(5)

其中ei是实际值与预测值之间的绝对误差，n是数据的总数．

本文基于数据库中292组试验数据，采用3层前馈神经网络模型，如图2所示．其中输入层为影响FRP筋与混凝土界面黏结性能的7个变量；输出层为黏结强度；隐藏层最佳神经元数量需要通过经验和试算确定．神经元数量足够多，才能正

图2 BP神经网络模型

确地对问题进行建模，但是又不能太多，以维持网络的泛化．通过测试多个网络后，确定了本问题的隐藏层神经元数量为13．

2 FRP筋与混凝土界面强度的预测模型

2.1 数据预处理

基于文献[20-28]，本文建立了292组FRP筋混凝土拉拔试验数据库．其中FRP筋类型由数字1～4表示，分别代表GFRP、CFRP、BFRP、AFRP；数字1～8分别代表黏砂、低肋、高肋、纤维束螺旋且带肋、纤维束螺旋及黏砂、纤维束螺旋且带肋并黏砂、纤维束螺旋和光圆8种FRP筋表面形式；数字1～4分别代表拔出、劈裂、锚固和FRP筋断裂4种试件破坏模式．具体输入和输出变量的最大值、最小值、均值和标准差见表1．

表1 数据库中输入和输出参数的范围

2.2 BP神经网络构建

利用Matlab中神经网络工具箱，对292组数据进行编程处理．数据库被随机分成两个数据集，其中242组数据用于训练，50组数据用于仿真预测．具体步骤如下：

(1)样本数据预处理．为提高神经网络的训练效率，将输入和输出样本数据进行预处理．本文采用premnmx函数对输入和目标数据集进行归一化处理，生成函数[p1，pmin，pmax，t1，tmin，tmax]=premnmx(P，T)，其中P和T分别为原始输入和输出样本数集；p1和t1为归一化后的输入和输出样本数集；pmin和pmax均是列向量，分别为矩阵P每一行的最小值和最大值；tmin和tmax分别为矩阵T每一行的最小值和最大值．

(2)预测模型生成及初始化．采用LM(Levenberg-Marquardt)算法的训练函数trainlm对网络进行训练，其优点是可以获得比其他任何一种算法更小的均方误差．结合对BP网络模型结构的设计和激活函数及训练函数的选择，以及测试多个网络后，隐藏层神经元数量匹配为13，网络生成函数表达为net=newff(minmax(p1)，[7，13，1]，{′tansig′，′tansig′，′purelin′}，′trainlm′)．其中net为生成的BP网络对象，newff 在生成BP网络时已对各层权值和阈值的初始化函数重新定义，并使用initff函数重新对网络进行初始化．

(3)模型训练及仿真．经过多次编程试算，得到网络中的主要训练参数取值如表2所示．在训练参数设置完成后，调用训练(train)函数对BP网络进行训练，具体表达为[net，tr]=train(net，p1，t1)．其中p1为归一化后的输入矩阵(矢量集)，即本文中影响FRP筋与混凝土界面黏结强度的7个变量；t1为对应归一化后的输出矩阵，即界面黏结应力；等号左、右两侧的net分别为训练后和训练前的网络对象；tr用于存储训练过程中的误差信息和步数信息．

表2 神经网络训练参数及取值

通过调用sim函数实现BP网络仿真，具体表达如下：

Ben and Baby are good friends.They can run fast.They don’t just run after a same ball.They also play with each other.When I hide myself in cabinets，they can always find me.They always do wonderful tricks on me.They like barking and fighting，so our home is noisy all the time.

pn=premnmx(p2)；

tn=sim(net，pn)；

t2=postmnmx(tn，tmin，tmax)

其中pn为归一化后的输入数据；tn为数据pn通过网络后的输出数据；net为训练好的神经网络；t2为最终的输出值，将其与试验值进行对比，分析该BP神经网络的预测结果．

3 预测结果分析

训练网络结构中学习速率设为0.01，最大允许步数为5 000步，目标网络误差设为0.000 01．该神经网络经过4 391次训练学习后，均方差为0.010 4，梯度为5.69×10-5．训练好的网络得到的权值和阈值包括输入层与隐藏层之间的权值w1和隐藏层与输出层之间的权值w2，以及隐藏层的阈值b1和输出层的阈值b2，具体见式(6)～(9)．

(6)

w2=(4.384 7 4.174 9 -2.876 2 2.322 2 -5.316 7 -3.076 1 -8.226 3 -3.588 7

-6.986 9 -5.288 7 -5.170 8 -4.875 6 -8.701 4)

(7)

b1=(-2.564 7 1.338 0 -4.035 3 -1.581 9 2.098 7 -2.297 2 0.184 7 -2.099 8

(8)

b2=(1.051 7)

(9)

基于BP神经网络得到的界面黏结强度计算值与试验值比较见图3，其中横纵坐标中的T和Y分别表示归一化后的黏结强度试验值和训练值，可以看出图中样本的训练值和试验值具有良好的相关性．此外，大部分的训练数集位于理想预测线Y=T附近，说明该网络已经具备了预测FRP筋与混凝土界面黏结强度的能力．

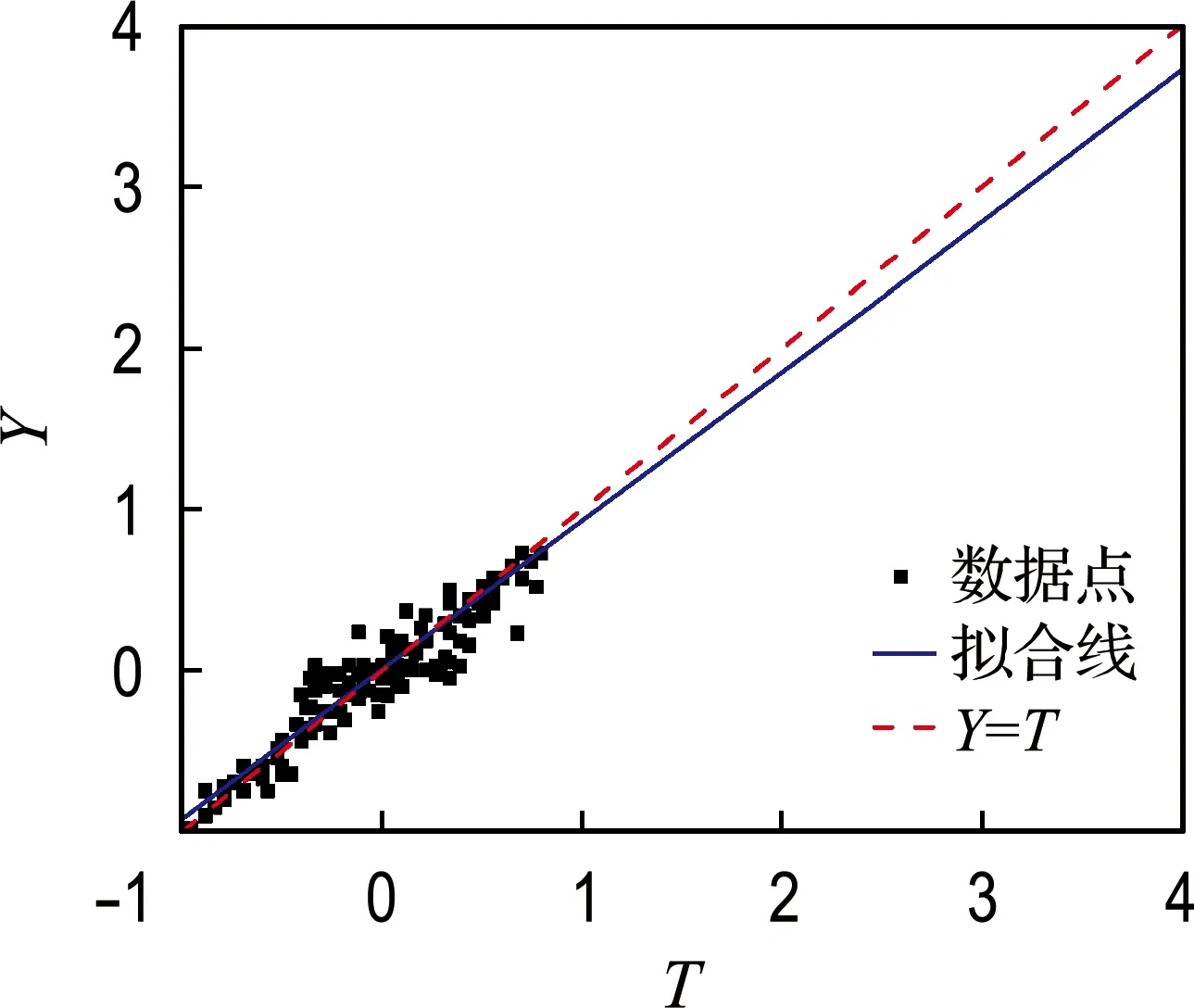
图3 界面黏结强度训练值与试验值比较

网络训练过程中的误差记录如图4所示，其中横坐标S表示训练步数，纵坐标M表示均方误差．从图中可以看出，在训练达到第250步左右，误差开始接近最小值；最终在第4 391步时，程序停止了训练，此时的均方误差达到了0.010 4，即达到最优状态．

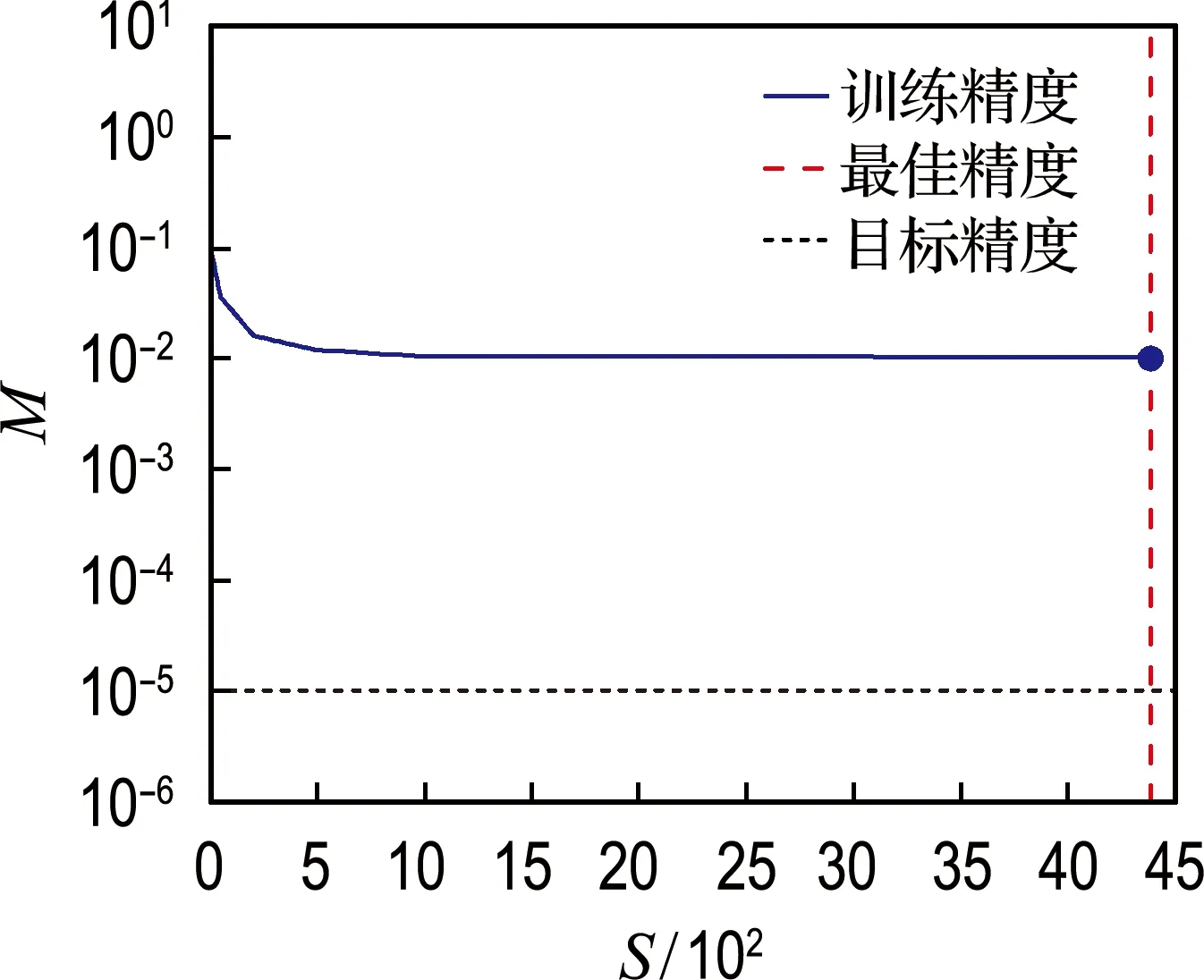
图4 网络训练过程中误差记录

为了更直观地反映本文建立的BP神经网络模型的计算误差，分别将不同阶段输出数据结果与试验数据进行对比，图5为训练结果与试验值的比较，图6为预测结果与试验值的比较．其中横坐标为试样编号，纵坐标τ为黏结强度．由图中对比可见，训练和预测模型中各样本的输出值与试验值分布基本一致．

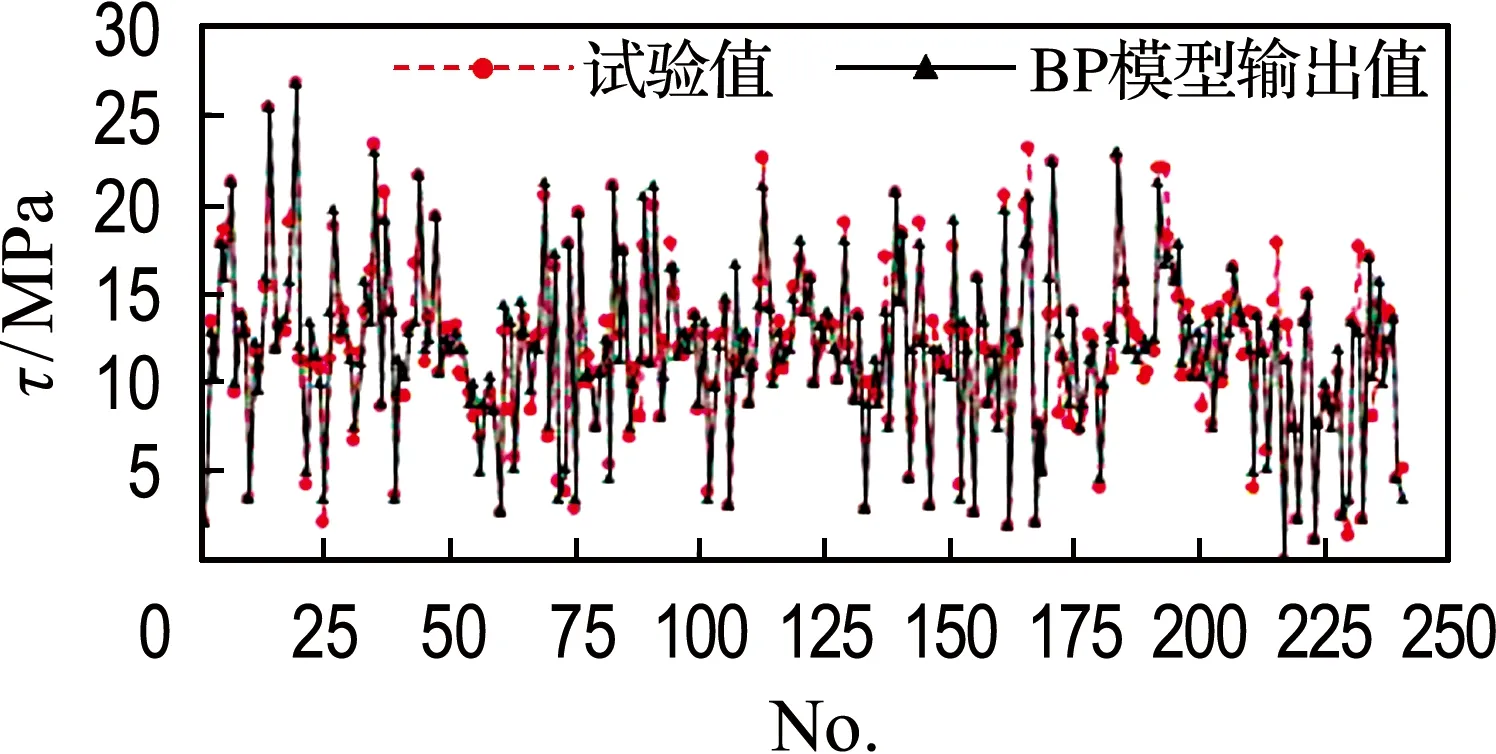
图5 训练中的BP模型输出值与试验值比较

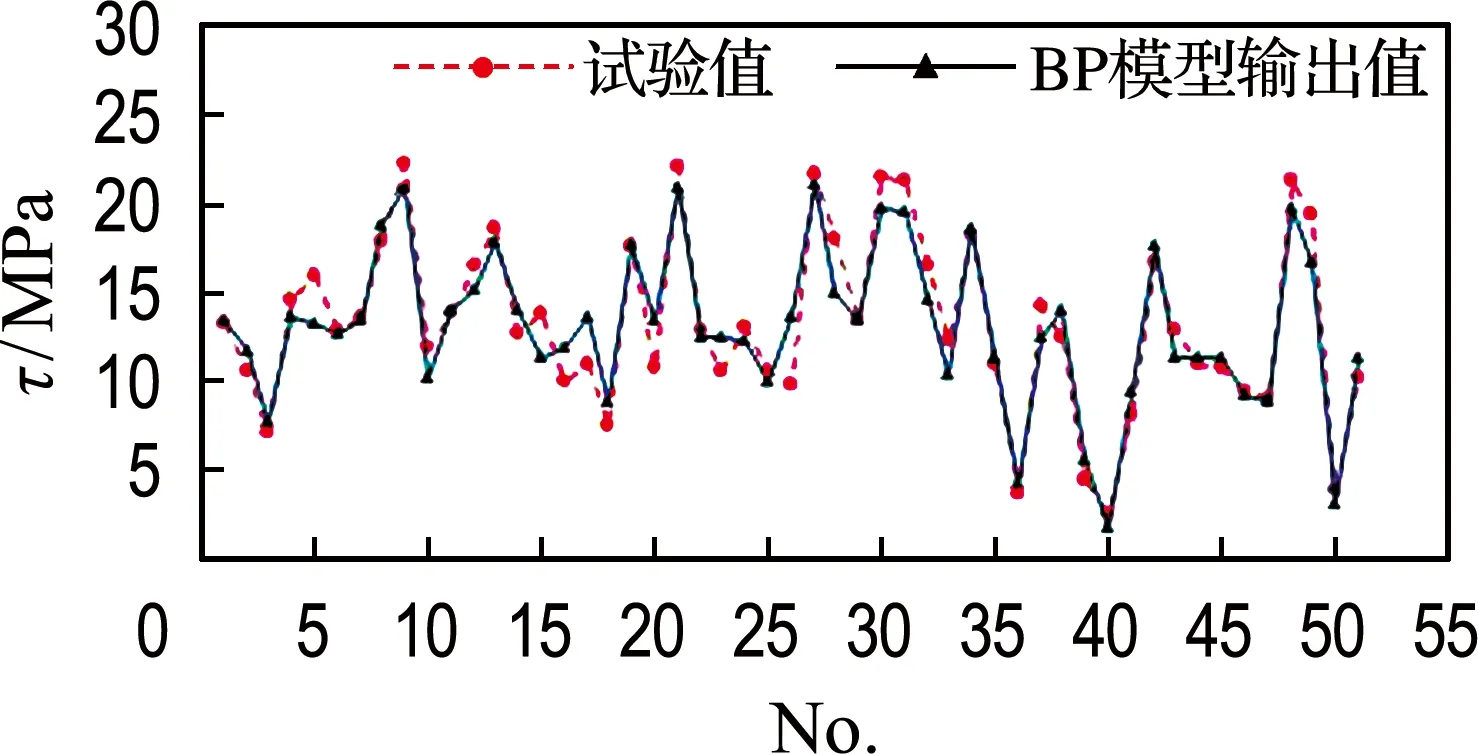
图6 预测中的BP模型输出值与试验值比较

图7为BP神经网络模型输出值与试验值散点图．训练值和预测值与试验值对比的均方差分别为0.926 5、0.909 6，说明该人工神经网络具有较高的预测精度．

基于242组数据训练的BP神经网络对50组试验数据进行预测，对比结果如表3所示，其中τu为黏结应力试验值，τe为黏结应力预测值，二者比值τe/τu的平均值为1.004 4，样本方差为0.136 69，变异系数为0.136 09．由此可见，本文建立的BP神经网络模型对FRP筋与混凝土界面黏结强度的预测值与试验值吻合较好，能够满足精度要求．

(a) 训练结果

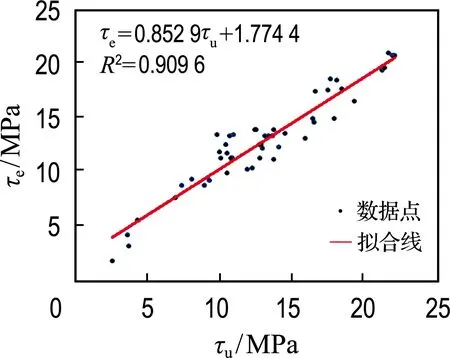
(b) 预测结果

表3 FRP筋与混凝土界面黏结应力与神经网络分析结果

4 结 语

FRP筋与增强混凝土材料的界面黏结性能受多种因素影响，在传统的理论分析中，建立包含众多影响因素的统一数学模型难以实现．本文基于ANN人工智能分析方法，建立了包含FRP筋类型、表面形式、FRP筋直径、锚固长度、破坏模式、混凝土抗压强度和归一化的混凝土保护层厚度7个影响因素，292组FRP筋与混凝土拉拔试验的数据库，通过学习和训练242组试件样本，建立了BP神经网络预测模型．对50组随机试件的预测结果分析可知，样本的训练值、预测值均与试验值吻合较好．FRP筋与混凝土界面强度的BP神经网络预测模型不受变量个数和变量间复杂关系的影响，在足够多的训练数据类型和数量基础上，预测结果能够达到较高精度，预测方法的通用性和可靠性也更强．