基于深度学习图像描述子的三维彩色点云配准

李 佳 骏， 安 毅， 秦 攀， 顾 宏

( 大连理工大学 控制科学与工程学院, 辽宁 大连 116024 )

0 引 言

通过将照相机和激光雷达联合标定，可以使激光扫描仪同时获取点云信息和颜色信息，得到更加接近真实世界的三维彩色点云数据[1]．因此，研究三维彩色点云数据配准在三维重建等领域具有重要的研究意义．点云配准是指将两组有重复区域的点云数据，通过计算点云间的刚性变换关系，最终使两组点云对齐在一个坐标系下，由此构建出完整的数据模型[2]．通常，迭代最近点法(ICP)[3]是解决这一问题的经典方法，但该方法仅适用于源点云和目标点云是预对齐的情况．如果点云较为稀疏或包含重复结构，则配准通常会因落入局部最小值而失败[4]．所以在点云配准前，首先要对点云进行粗配准，即将两片点云初步匹配到一个坐标系下，使源点云和目标点云之间获得良好的初始位姿．在此基础上，使用ICP或其改进的算法[5]进行精配准，进一步提高配准精度．

现阶段已经有许多点云粗配准算法，按照点云局部描述子类型可以将其分为两类．第一类是利用点云本身的几何信息和拓扑信息设计点云局部描述子，如3D-SIFT[6]、Harris 3D[7]和SHOT[8]等．Rusu等[9]首先提出了点云数据的快速点特征直方图(FPFH)特征，提取关键点特征后，使用采样一致性初始配准算法计算出点云的初始变换矩阵完成点云粗配准[10]．郑德华等[11]根据点云的点线面几何特征形成约束条件对点云配准参数进行计算．虽然传统的点云局部描述子为特征点提供了良好的判别能力，但不能分析点云带有的颜色纹理信息，且依赖于特定应用场景．第二类方法是建立点云中的点和图像中的像素之间的映射关系．通过将点云数据中的点映射到二维平面，利用图像中成熟的技术方法，计算点云局部特征描述子．比如，Elbaz等[12]将三维点云数据划分为局部超点集并投影为深度图，利用深度自动编码器计算点云匹配．Lin等[13]将点云转换为二维方位角图像，采用二维图像中的特征计算方法SURF[14]来寻找两幅图像之间的匹配像素对再寻求匹配关系．另外，包竹等[15]提出了用点云信息在投影平面上获得深度图像，采用ORB[16]算法在深度图像上完成对点云的粗配准．但以上这些研究大都是针对点云数据或点云生成的深度图像，没有有效利用三维彩色点云数据中包含的图像信息．另外，直接采用传统算法SIFT[17]、SURF、ORB等进行点云匹配，可能出现配准精度低的现象．而随着学习型描述子在二维图像局部描述子领域的应用逐渐广泛，TFeat[18]、L2-Net[19]、HardNet[20]等卷积神经网络结构可以从图像中计算出适用性更加广泛的深层特征．另外，近年还有一些针对基于深度学习的三维点云特征描述子研究，如PointNet[21]、2D3D-MatchNet[22]、3DSmoothNet[23]等三维卷积神经网络，但是三维卷积神经网络的模型一般较大，精度提高的同时计算效率较低，难以应用．

随着深度学习在点云局部描述子的研究中不断显示出优越性，大尺寸的模型对于硬件设备要求也带来了挑战，实用性降低．因此，本文充分利用点云数据中的图像信息，针对二维浅层卷积神经网络进行研究．

三维彩色点云数据同时具有点云的空间位置信息和颜色信息，并与图像中的像素存在一一对应关系．因此，针对三维彩色点云数据，本文提出一种基于图像特征的局部描述子点云配准方法，其主要思想是：首先，计算点云投影图的特征点；其次，由卷积神经网络和方向梯度直方图结合产生图像描述子作为点云局部描述子；然后，根据描述子之间的对应关系，找到匹配的点云特征点；最后，根据对应点云特征点，完成对点云的粗配准．

1 数据来源及图像匹配训练集构建

1.1 数据来源

本文针对三维彩色点云数据进行处理，需要保证该数据的精确性和可靠性．本文采用的点云数据采集工具是德国西克公司生产的LMS511-10100 PRO激光扫描测距仪．该激光扫描测距仪利用激光-时间飞行的原理以及多重回波技术实现对较远距离物体的测量，其抗干扰性能好．另外，图像信息由CCD工业相机Genie HC1024采集，在实际应用中能采集到低噪声、高速的稳定彩色图像．在实际采集系统中，在激光扫描测距仪顶端固定相机，利用旋转台将二者固定，在电机的驱动下使它们保持相同的角度匀速转动，由此搭建信息采集系统[24]，最终获得具有颜色信息的三维点云数据．图1是搭建的信息采集系统组成框图．

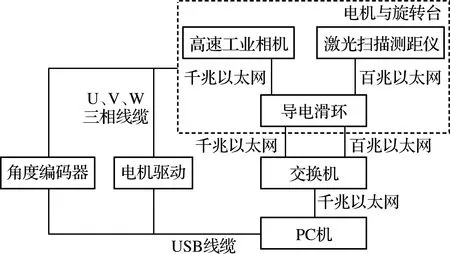
图1 采集系统组成框图

1.2 基于网格运动统计法的训练集构建

一般利用深度学习训练孪生神经网络均采用liberty、yosemite和notredame等局部图像块数据集[25]，但是这可能导致神经网络在点云投影图场景适用性较差．为此，本文采用基于网格的运动一致性算法，提出一种在点云任意场景下构建图像匹配数据集的方法．

构建适用于点云场景的局部图像块训练数据集，本质上是要得到大量高质量的匹配点．GMS[26]是一种基于运动的平稳性，利用网格统计邻域支持量，用大量的特征匹配有效滤除错误匹配，从而获得大量准确的图像匹配结果的算法．本文采用精度更高的SURF算法代替GMS采用的ORB算法，使最终得到的匹配更加准确，数据集更加具有可靠性．

图2为正确匹配对与错误匹配对的分布图，若两幅图像Ia、Ib的特征点集合分别为N、M，则从Ia到Ib特征匹配的集合可以表示为X={x1，x2，…，x|N|}，其中xi表示其中的一对匹配，即xi={α，β|α∈N，β∈M}．特征点α、β周围的邻域分别用a、b表示，对于给定半径r，定义特征点邻域：

(1)

根据运动的平滑性，若该匹配对正确，则邻域a、b之间应存在其他若干对匹配关系；若该匹配对错误，则邻域a、b之间不存在其他匹配关系．已知a、b邻域之间存在某一xi匹配，则邻域a、b之

图2 正确匹配对与错误匹配对分布

间所有的匹配记作Xi．用Si表示xi的邻域支持量，即a、b邻域之间其他匹配对的数量，则有：

Si=|Xi|-1

(2)

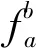
(3)

其中m表示区域b中的特征点数量，σ是权重值，0<σ<1．

(4)

(5)

根据上式，当xi是正确匹配时，Si～B(n，pt)；当xi是错误匹配时，Si～B(n，pf)．

为了使计算复杂度降低，将图像划分为G=g×g个网格，通过计算两个待匹配网格各自周围相邻格子的估计量，得到网格对的邻域支持量．

(6)

其中K表示与匹配xi一起连续的不相交区域的数量；{ak，bk}表示对应的网格块，Xk表示在{ak，bk}区域对上的匹配．由此得到，当Xk匹配时，Si～B(Kn，pt)；当Xk不匹配时，Si～B(Kn，pf)．因此，两种情况下Si的均值和标准差如下：

(7)

由于运动网格的划分，根据计算的均值和标准差，得到网格区域匹配对二值化表达式：

(8)

式中：i表示图像Ia中的第i个网格区域；j表示图像Ib中的第j个网格区域；pair{i，j}表示网格对匹配的结果；Sij表示判断图像块i和j是否匹配的阈值；μ为权重值；ni表示K个网格块中特征点的平均数量．根据这种网格运动统计法可以从大量匹配中有效剔除误匹配，得到大量正确匹配点．因此，结合传统SURF特征提取算法和GMS算法可以提取出大量相匹配的图像块，生成训练数据集．

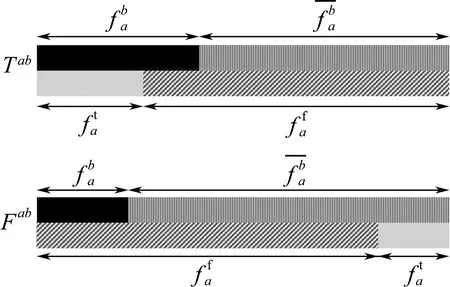
图3 fa特征点匹配的事件空间

2 组合描述子的构建

2.1 基于卷积神经网络的图像局部描述子

传统描述子一般为人工设计，且通常需要丰富的经验来设计和优化，另外可能存在泛用性较差的问题．而学习型描述子在解决图像识别、检索等领域的问题时具有较大优势．因此，更多人采用卷积神经网络提取关键点邻域的深度特征作为描述子．由于目前已有的网络结构都比较深，模型尺寸较大，难以满足多样的环境需求．TFeat的模型是L2-Net、HardNet的一半，是3DSmoothNet的1/10．同时，TFeat的运算速度和效率较2D3D-MatchNet[22]和DeepDesc[27]快50倍，且在GPU的加速下，可与Fast特征描述子相媲美[18]．因此，基于TFeat的浅层神经网络结构在应用中更便于满足环境需求，并搭载到硬件资源中使用．所以，本文采用TFeat网络结构计算特征描述子．

TFeat是一种三分支网络结构，训练数据集为成对的正样本和单个负样本．其单支网络结构如图4所示．该单支网络的输入为32×32的图像块，输出是128维描述子，分别用d0，…，d127表示．在实际训练过程中通常负样本远多于正样本，即出现数据集不平衡的问题．若采用随机采样策略[18]构建训练三元组，会降低训练效率；采用最难区分负样本挖掘策略[20]准确度更高，但是构建三元组极大增加了前期数据处理的开销．因此，本文采用了批处理策略[28]，训练损失函数为

(9)

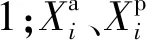
图4 TFeat单支网络结构

2.2 基于方向梯度直方图的局部描述子

由于适用于局部目标的方向梯度直方图(HOG)[29]可以很好地描述图像块的全局性特征，HOG描述子也可以作为关键点的局部描述子．HOG算法利用图像局部区域的方向梯度直方图来构成特征，步骤为：对图像进行归一化，利用一阶模板算子分别从横向、纵向计算梯度，求得检测窗口的梯度图像；在梯度图像上滑动窗口，每个窗口被分为更小的单元；在每个单元中计算梯度幅值和梯度方向并进行统计，将所有直方图向量连接，即可得到图像块的局部描述子．本实验中图像块大小为32×32．若将HOG算法中方块的边长设置为16，间隔为8，单元大小为8×8，单元直方图方向数量为9，则对每一个关键点计算HOG特征可得到324维描述子．

因此，本文将卷积神经网络提取出的128维局部特征与324维HOG局部特征进行特征融合，形成452维组合特征描述子，进一步计算匹配关系和点云刚性变换关系，完成点云的粗配准．

3 实验结果与分析

3.1 实验环境搭建

实验平台为Windows 7 64位操作系统，处理器为Intel Core i5-5200U，内存为8 GB，编程环境为VS2017、OpenCV3.4.2、PCL1.9.0，开发语言为C++、Python．本实验采用的两幅三维点云数据的源点云点数为284 617，目标点云点数为305 681．

3.2 实验结果分析

本文通过构建组合描述子模型对点云数据进行配准．于是，将实验结果分为两个部分．第一部分，验证文中所提出的适用于点云场景的局部图像块训练数据集的可靠性．第二部分将文中所提出的组合描述子应用于点云粗配准，并对实验结果进行讨论．

根据激光扫描测距仪的数据采集原理，将完整的三维彩色点云数据投影生成图像．为了生成局部图像配准数据集，对于两张图像分别提取特征点并计算图像的匹配点对，将计算的图像匹配点对分别以特征点为中心提取周围32×32的图像块．故图像中匹配点对的准确性将直接影响到图像匹配数据集的精度．图5(a)是采用SURF描述子计算的匹配点对；图5(b)是采用SURF+GMS描述子计算的匹配点对．

(a) SURF生成图像匹配点对

(b) SURF+GMS生成图像匹配点对

由图可知，应用于点云投影图时直接采用SURF算法计算匹配点对，出现大量的误匹配，严重影响所提取的局部图像块训练数据集的精度．这可能是由于点云投影图中大量存在的像素缺失造成的影响．而本文采用的结合SURF+GMS的算法计算的匹配点对则更加准确，保证了训练数据集的可靠性．因此，本文利用SURF+GMS算法建立场景丰富的训练数据集，训练特征提取卷积神经网络．

为了全面对比本文方法与其他传统特征提取算法在三维彩色点云配准中的算法性能，采用多种指标对点云配准进行评价．本文选择的评价指标为算法产生的特征点数量、匹配点对数量、完成粗配准所用时间，以及将源点云配准到目标点云坐标系后匹配点对的均方根误差(RMSE)．实验结果见表1．

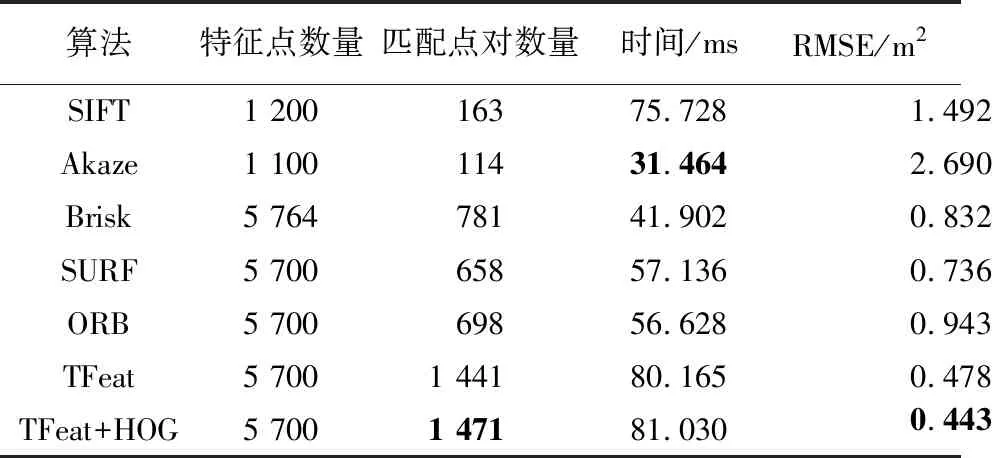
表1 不同算法结果比较

根据表1可知，特征点数量会对匹配点对数量造成影响，进一步影响匹配效果．SIFT和Akaze 算法特征点数量较少，相应得到匹配点对数量也较少，RMSE较高，表明这两种算法不适用于彩色点云场景；其余算法均可以通过控制参数使得提取到的特征点数量几乎一致．TFeat+HOG组合特征描述子可以生成更多的匹配点对；时间消耗略有提升，与SIFT接近；配准时RMSE最低，表明本文所提出的组合描述子在粗配准精度上具有较大优势．

通过将各算法得到的粗配准结果进行ICP精配准，可以进一步分析各算法粗配准的效果．本文采用拟合分数作为评价指标，实际上是计算配准后源点云对应目标点云中最近点距离的平方和，将其简记为F．

(10)

将拟合分数与ICP迭代次数绘制折线图，其中拟合分数记作F，迭代次数记作T，最终结果如图6所示．

图6 各算法精配准结果比较

由图可知，与其他图像特征提取描述子对比，基于本文方法的粗配准结果在未进行精配准时，拟合分数最低；迭代次数一定时，组合描述子的拟合分数最低，进一步证明了本研究精配准精度最高，并且能够快速收敛，减少精配准的时间消耗．另外，传统图像算法SURF随迭代次数增加，拟合分数几乎不变，说明陷入了局部最优解．但SURF+TFeat+HOG能够快速收敛至全局最优解，配准结果更好．实验表明了本文方法用于彩色点云粗配准，不仅能得到更加精确的初始位姿，在后续精配准时减少时间损耗，而且避免陷入局部最优解，进一步证明了本文提出方法的可行性．本文提出的方法充分利用了三维彩色点云中的图像信息，相比于传统图像算法，得到了更好的配准效果，更加明确了图像信息在三维彩色点云数据中的重要作用．

4 结 语

本文针对在各种应用场景提取局部图像匹配块数据集的需要，提出一种基于网格运动统计法的图像匹配数据集提取算法，并利用该算法生成训练数据集．另外，由于以往点云配准算法未利用三维彩色点云数据中的图像信息，本文设计了一种融合深度图像描述子和方向梯度直方图局部描述子的局部特征组合描述子．将该方法应用于点云粗配准，能有效利用两种描述子的特性，提高点云投影图中匹配点对的准确性，进一步改善点云粗配准效果．但是该方法存在的局限是，配准时寻找点云与图像像素的对应关系上消耗的时间相对较长．如果能快速获取对应关系，则能明显提高实际应用效率．文中还综合比较了在点云投影图中应用各种传统图像配准算法的实际效果，为研究者们进一步研究利用点云与图像之间的映射关系解决点云领域的相关问题提供解决思路．