基于退化检测和优化粒子滤波的轴承寿命预测方法

许 雨 晨， 李 宏 坤， 马 跃， 黄 刚 劲， 张 明 亮

( 大连理工大学 机械工程学院， 辽宁 大连 116024 )

0 引 言

工业领域中高端装备的系统日趋复杂，综合化、智能化程度不断提升，运行过程中维护和保障的成本也越来越高．由于设备组成环节的增加及各环节之间的高耦合性，发生故障和性能失效的可能性逐渐上升，因此重大装备的预测和健康管理(prognostics and health management，PHM)技术逐渐成为研究热点[1]．轴承作为工业领域的“心脏”，在各种机械设备中使用广泛，是保障设备正常运行的核心零件，一旦轴承发生故障，将对整个设备的运行造成影响，导致安全事故和经济损失的发生，因此研究轴承的寿命预测方法具有重要价值．

文献中指出大致可以将机械设备的寿命预测方法分为基于失效物理的方法、基于数据驱动的方法和融合方法[2]．基于失效物理的方法根据机械的故障机制或损伤原理建立数学模型来描绘机械的退化状态，具有较高的预测准确度．但随着机械设备日趋复杂化，很难根据故障机理建立精确的模型，因此这种方法的应用领域具有较大的局限性．近年来随着机器学习的发展，基于数据驱动的方法成为寿命预测领域中热门的研究方向．数据驱动的方法不依赖专业的经验知识，也不需要建立精确的数学模型，而是从历史数据中自动学习设备的退化信息，从而对未来趋势进行评估和预测．主流方法有神经网络、回归模型、支持向量机、模糊理论、卡尔曼滤波和粒子滤波(particle filter，PF)等．融合方法是通过两种及两种以上方法的结合，将多种方法的优势进行整合的预测方法．

虽然目前神经网络、支持向量机等传统数据驱动的方法在寿命预测领域中已得到广泛研究及应用，但是在处理长期预测的不确定性问题上仍存在缺陷．针对这个问题，专家学者们提出使用贝叶斯滤波算法来解决[3]，其中粒子滤波是应用最为广泛的方法之一．基于贝叶斯滤波框架的寿命预测能够给出剩余寿命的概率分布，改善长期预测的不确定性问题，并且相较于单一的预测值，更具参考价值[4]．Baraldi等[5]将粒子滤波与人工神经网络结合，对疲劳裂纹扩展进行了有效预测．Deng等[6]使用粒子滤波框架对锂电池寿命进行了预测，得到了较好的预测结果．Peng等[7]以飞机发动机数据集为例，通过深度置信网络构建了健康指标，采用粒子滤波算法对其寿命进行了预测，验证结果表明该方法在寿命预测的不确定性表征方面具有较好的性能．虽然粒子滤波在处理长期预测的不确定性问题上有优势，但其算法本身仍有缺陷[8]，需要深入研究．

数据驱动的轴承寿命预测方法中一个关键环节是确定开始预测的时刻[9](time to start prediction，TSP)，因为TSP对寿命预测的准确性有重要影响．目前检测TSP的常用方法有主观确定、3σ方法、系统最长时间常数等，大多使用的是统计方法，不能针对某个系统自适应检测．

为解决上述问题，本文提出一种基于退化检测和优化粒子滤波[10]的轴承寿命预测方法．该方法首先利用轴承原始振动信号构建一个能够全面描述轴承衰退过程的退化指标，并通过所建立的退化指标对轴承进行自适应退化检测，确定开始预测的时刻，然后使用粒子群优化算法对常规粒子滤波进行改进，提高算法的预测精度，应用于轴承的寿命预测．

1 粒子滤波

1.1 粒子滤波算法

粒子滤波是一种基于蒙特卡罗采样的贝叶斯估计算法．该算法的本质是使用一系列具有对应权值的随机样本点近似系统状态的后验概率密度，从而得到系统状态的最小方差估计[11]．该算法在非线性、非高斯系统的状态参数估计中具有明显优势，目前已经广泛应用于机械设备及锂电池等寿命预测研究中[12]．本文通过建立轴承的动态模型，并基于粒子滤波算法对模型参数进行估计，从而得到未来时刻轴承的系统状态．

一般系统的动态模型包括状态转移方程和量测方程，可以表示为

xk=fk(xk-1，vk-1)
zk=hk(xk，wk)

(1)

式中：xk表示系统在k时刻的状态变量；fk：Rnx×Rnv→Rnx表示系统的状态转移方程；zk表示系统在k时刻的量测值；hk：Rnx×Rnw→Rnz表示系统的量测方程；vk和wk分别表示系统的过程噪声和量测噪声．

贝叶斯滤波算法是对系统状态的后验分布进行求解，首先利用动态模型对k时刻系统状态的先验分布进行预测：

(2)

式中：p(xk|xk-1)由系统的状态转移方程定义．

当新的量测值到来时，对先验分布进行更新，得到k时刻的后验分布：

(3)

式中：p(zk|xk)由系统的量测方程定义；p(zk|z1：k-1)为归一化常数，具有如下形式：

(4)

式(2)和(3)的计算过程涉及大量髙维积分运算，难以求解，因此采用蒙特卡罗采样来解决这个问题．通过蒙特卡罗方法可以将k时刻的后验分布离散加权为

(5)

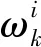
(6)

(7)

由于常规算法中建议密度函数使用的是系统状态的先验分布，舍弃了当前时刻的量测值，因此出现了一些问题[10]．尤其当似然函数很窄或者位于先验概率分布的尾部时，经过几次递归，大部分粒子权值将会变得很小，粒子权值的方差将会增大，即出现粒子退化现象．粒子退化现象是粒子滤波无法避免的问题，致使该方法在实际应用中不能达到预期的滤波效果．为改善这个缺陷，方法之一是驱动粒子向高似然区域移动，因此本文引入粒子群优化算法，对重要性采样过程进行优化．

1.2 粒子群优化粒子滤波算法

1.2.1 粒子群优化算法 粒子群优化算法是一种群智能寻优算法，该算法模拟鸟类的捕食行为，通过鸟群中个体之间传递信息来搜索最优解．该算法理论简单、易于实现，因此在相关领域中的研究应用极为广泛．

粒子群优化算法实现的基本思路为

(1)随机初始化一群粒子，样本容量为M，这群粒子仅具有速度v和位置x两个属性．

(2)定义适应度函数，计算出每个粒子的适应度值，找到每个粒子当前的个体最优值Pbest；通过信息共享找到整个群体中最优的粒子，并将最优粒子的个体最优值Pbest作为全局最优值Gbest．

(3)利用下式对粒子的速度和位置进行更新：

vi=ω×vi+c1×r×(Pbesti-xi)+c2×r×

(Gbest-xi)

(8)

xi=xi+vi

(9)

式中：vi表示每个粒子的速度；ω称为惯性权重；c1、c2统称为学习因子；r是分布于(0，1)的随机数；xi表示每个粒子的位置．

(4)返回步骤(2)，直至满足结束条件．

为提高粒子群优化算法的寻优性能，本文使用参数动态调整的速度更新公式．粒子群优化算法倾向于在运行初期进行广泛搜索，在运行后期进行局部求解．因此使用动态调整的惯性权重，可以改善算法性能．本文使用线性惯性权重，其值根据迭代次数动态变化，计算公式如下：

(10)

式中：ωmax、ωmin分别为惯性权重的最大值和最小值，t为当前迭代次数，tmax为最大迭代次数．

学习因子分为个体学习因子c1和群体学习因子c2，c1表示粒子向自身经历的最优值学习的能力，c2代表粒子向群体经历的最优值学习的能力．对学习因子进行动态调整，也能改善算法的求解性能．因此本文算法中使用了动态学习因子，迭代初期，要使粒子在全局范围内进行广泛搜索，增加粒子的多样性，则需要设置较大的个体学习因子c1；而搜索后期则需要设置较大的群体学习因子c2，来加快算法的收敛速度．本文使用的动态学习因子计算公式如下：

(11)

式中：cmax、cmin分别为学习因子的最大值和最小值．

1.2.2 粒子群优化粒子滤波算法 通过1.1节内容的介绍可知，常规粒子滤波算法中重要性采样使用的建议密度函数是次优的，导致算法滤波性能不够精确，因此本文对重要性采样过程进行改进，形成粒子群优化粒子滤波算法．常规算法中采样的粒子样本分布与真实的后验概率分布差距较大，无法对系统状态进行有效估计．而粒子群优化算法引入了当前观测值，能够驱动粒子向高似然区域移动，所以优化的结果是大部分粒子都能分布在真实状态附近，从而提高了滤波精度[10]．

改进算法的实现步骤如下：

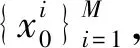
(12)

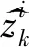
利用1.2.1节中所描述的粒子群优化算法，对从先验分布中采样的粒子分布进行优化，然后根据下式计算重要性权值并归一化：

(13)

(14)

归一化权值为

(15)

(3)重采样．重新采样，并将所有粒子权值重置为1/M．

(4)输出．使用下式对系统状态进行估计：

(16)

(5)k=k+1，新的量测值到来，返回第(2)步，直至退出算法．

2 轴承退化检测

基于数据驱动的轴承寿命预测过程中，有个关键问题需要解决，即确定开始预测的时间(TSP)．检测轴承开始出现退化迹象的时刻，将其作为TSP．正确检测TSP可以改善轴承寿命预测的性能，因此本文引入一种轴承退化检测方法，分为以下两步：构建退化指标和退化检测．

2.1 构建退化指标

本文通过特征融合构建退化指标，具体步骤如下：

(1)特征提取

本文分别提取时域、时频域和基于三角函数的特征组成候选特征集．提取的候选特征如下．时域特征：F1，均值；F2，标准差；F3，最大值；F4，最小值；F5，均方根；F6，峭度；F7，峰值；F8，峰峰值；F9，偏斜度；F10，熵值；F11，峰值指标；F12，脉冲指标；F13，峭度指标；F14，裕度指标；F15，波形指标；F16，偏斜度指标．时频域特征：F17～F24，IMF能量值．三角函数的特征：F25，IHC标准差；F26，IHS标准差．时频域特征提取方法是对原始振动信号进行集成经验模态分解(ensemble empirical mode decomposition，EEMD)得到8个本征模态分量(intrinsic mode function，IMF)，计算每个IMF的能量作为特征值．两个三角函数特征分别为反三角双曲余弦(inverse hyperbolic cosine，IHC)标准差和反三角双曲正弦(inverse hyperbolic sine，IHS)标准差[13]．此类三角函数可产生低尺度特征，并具有更好的趋势性，计算公式如下：

(17)

(2)特征优选

候选特征集中的退化特征对故障发展的敏感度有很大差别，为进行有效预测，需选取敏感度高的特征用于构建退化指标．本文首先使用时间相关性、单调性和鲁棒性对候选特征进行评估．相关性表征了特征与时间序列的线性相关度，单调性用于描述特征持续增大或减小的趋势，鲁棒性反映特征对异常值或噪声的容忍度．

采用移动平均法对特征进行平滑处理，得到退化特征的趋势部分和残差部分：

X(tk)=Xt(tk)+Xr(tk)

(18)

式中：X(tk)为退化特征，Xt(tk)为退化特征的趋势值，Xr(tk)为退化特征的随机值．

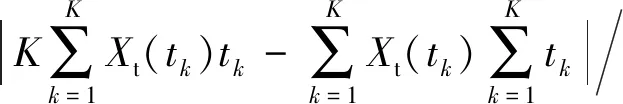
(19)

(20)

(21)

式中：K是原始数据长度，tk表示时间序列．

单一的评价指标只能从特定角度衡量退化特征对故障发展的敏感度，并且对于同一个退化特征，评价指标间也可能出现不一致的情况．因此需要将3个评价指标综合起来，对退化特征进行优选[14]．所以本文将3个指标的线性组合作为综合评价指标，计算公式如下：

s.t.ωi>0

(22)

式中：J为综合评价指标；Ω为候选特征集；ωi为单一评价指标的权重，本文中选取ω1=0.4，ω2=0.3，ω3=0.3．从上式中可以看出综合评价指标与单一评价指标具有正相关关系，因此综合指标值越大，说明退化特征的敏感度越高，比较适用于寿命预测．

(3)特征融合

通过上文中特征选择步骤，得到一个包含P个特征的优选特征集，为构建一个能够较为全面反映轴承故障信息并具有较好趋势性的指标，本文使用加权融合方法将优选特征集中的退化特征进行融合，建立退化指标．方法步骤如下：

步骤1计算每个优选特征的权重．使用相关性评价指标作为加权融合算法中的权重值，并将其归一化：

(23)

式中：Ci是第i个特征的相关性评价指标．

步骤2计算优选特征集中每个特征的前s个点的均值Vi，作为轴承健康阶段的特征值：

(24)

式中：Xi，k为第i个特征k时刻的值．

步骤3计算健康阶段特征值和当前时刻特征值之间的距离，然后使用步骤1中的归一化权重进行加权融合：

(25)

式中：Dt为t时刻退化指标的值．

使用局部加权回归算法平滑处理构建的退化指标，并将时间间隔设为1 min，进行重采样，得到最终的退化指标．

2.2 退化检测

上文中建立的退化指标反映了轴承的运行状况，轴承运行正常时，退化指标变化平稳，随着运行时间的增长，轴承逐渐出现损伤，退化指标则会反映出轴承的故障演化过程．一旦轴承出现退化迹象，指标值就会出现较大幅度的增长，说明轴承进入了退化阶段，需要从此时开始进行寿命预测．退化检测在寿命预测工作中是极为关键的环节，错误识别的TSP会导致遗漏与早期故障相关的有用信息，或者将正常运行的数据并入预测结果中[15]．这些情况都会影响预测结果的精度，因此确定准确的TSP具有重要意义，然而目前检测TSP的方法大多使用的是统计方法，常用方法有3σ方法、系统最长时间常数等，这些方法都无法针对特定系统自适应调整，为此本文提出一种自适应退化检测法，通过衡量退化指标的增长幅度来确定TSP．

首先确定一个窗口长度为l的滑动窗，使用滑动窗口中l个样本计算退化指标的梯度值[16]，窗口中l个样本的梯度值可由下式得到：

(26)

式中：gi为第i个窗口的梯度值，Di为第i个窗口中l个退化指标的值．如果第i个窗口中计算的gi大于设置的阈值，就可以认为轴承开始退化．图1为自适应检测TSP的方法．

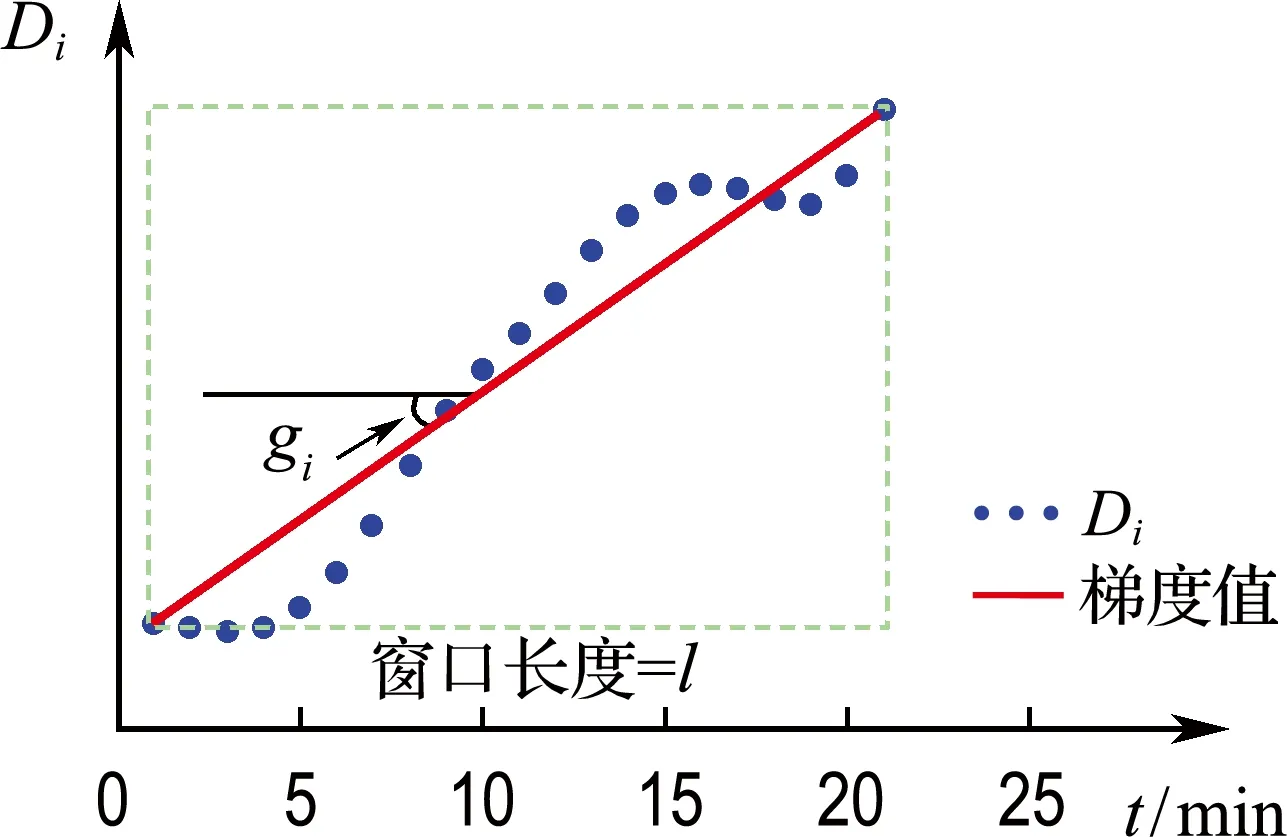
图1 TSP检测方法

3 基于PSO-PF的轴承剩余寿命预测方法

本文首先构建了一个加权融合的退化指标，并检测开始预测的时刻(TSP)，然后利用PSO-PF算法从检测到的TSP开始对轴承剩余寿命进行预测．方法流程图如图2所示．

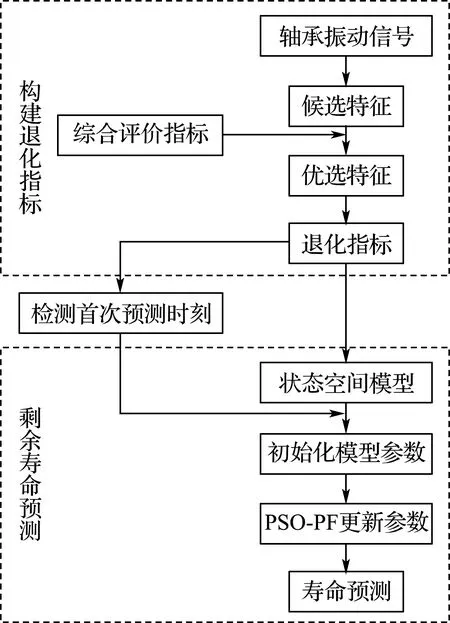
图2 方法流程图

本文使用Pairs-Erdogan裂纹扩展模型[17]描述轴承的退化过程，故障尺寸增长率可由下式表示：

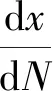
(27)

式中：x为故障尺寸；N为材料的疲劳寿命；C0和m为与材料相关的常数；ΔK为应力强度因子，表达式如下：

(28)

式中：β为与材料相关的参数．

将式(28)代入式(27)可得

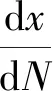
(29)

假设量测值zk和状态值xk存在线性关系，根据一般系统的动态模型，将上式改写为如下形式：

(30)

式中：A和n为需根据观测值进行估计的未知参数．

建立了轴承退化模型后，便可利用1.2节中提出的粒子群优化粒子滤波算法对轴承剩余寿命进行预测，预测的具体步骤如下：

(1)退化检测．首先使用局部加权回归算法平滑处理退化指标，并进行等距重采样；然后利用自适应退化检测法确定轴承首次预测的时间点．

(2)将已知数据序列代入状态转移方程中，对模型参数A和n进行非线性最小二乘拟合，得到模型参数的初始值．

(3)使用改进的粒子滤波算法对模型参数不断调整，待更新结束后，将最新的估计值作为模型参数，对轴承未来状态进行递推预测，对剩余寿命分布进行估计．

4 实验及结果分析

4.1 实验介绍

本文的实验数据来源于FEMTO-ST研究所的PRONOSTIA轴承实验台进行的轴承加速退化寿命实验，实验台结构如图3所示．实验中为加快轴承退化速度，使用了加载装置对其施加径向力，将其全寿命周期缩短到数小时之内．该实验中轴承转速为1 800 r/min，采样频率为25.6 kHz，采样时间为0.1 s，负载为4 000 N，每隔10 s进行一次采样．当振动幅值大于20g后，轴承视为失效．图4为本文算法验证所用的轴承1和轴承2的振动信号，从图中可以看出轴承运行前期振动幅值很小且波动平稳，到运行末期振动幅值迅速增大，很短时间内振动幅值达到失效阈值．

图3 PRONOSTIA轴承实验台

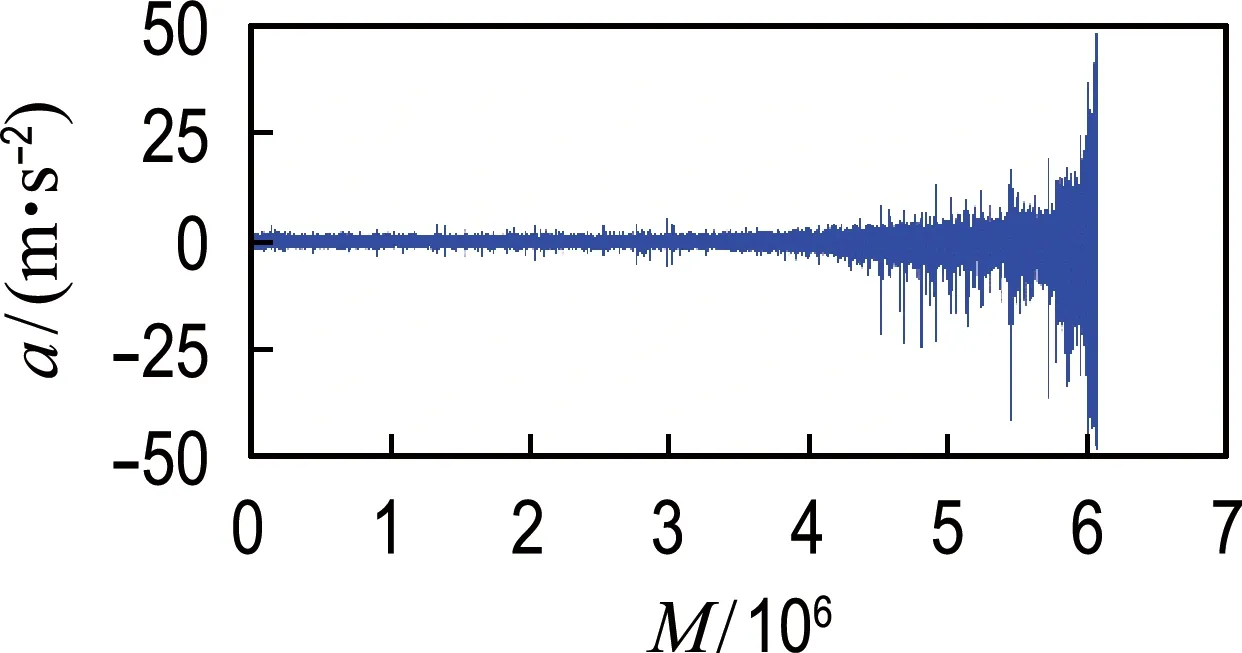
(b) 轴承2振动信号

4.2 轴承剩余寿命预测

从轴承1和轴承2的振动信号中提取2.1节中所述的26个候选特征，使用综合评价指标J进行评估，评估结果如表1所示．轴承1最优特征和最差特征对比如图5所示，轴承2最优特征和最差特征对比如图6所示．从图中可以非常直观地看出综合评价较高的特征具有更好的时间相关性及单调性，而综合评价较低的特征对故障的发展并不敏感，说明本文使用的特征选择方法是有效的．对于轴承1和2分别选取前14个候选特征组成优选特征集，对其进行加权融合得到退化指标；然后对其进行平滑处理，并按时间间隔为1 min进行重采样．

表1 候选特征综合评价

为验证融合后的特征更适用于寿命预测，对试验轴承的原始特征和融合特征的时间相关性进行比较．从表2中可以看出融合特征的时间相关性较高，说明具有更好的趋势性，同时融合特征又包含较全面的故障信息，因此相较于单一原始特征更适用于寿命预测．

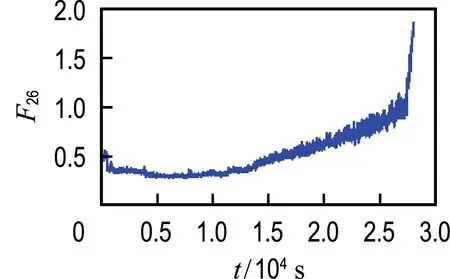
(a) 最优特征

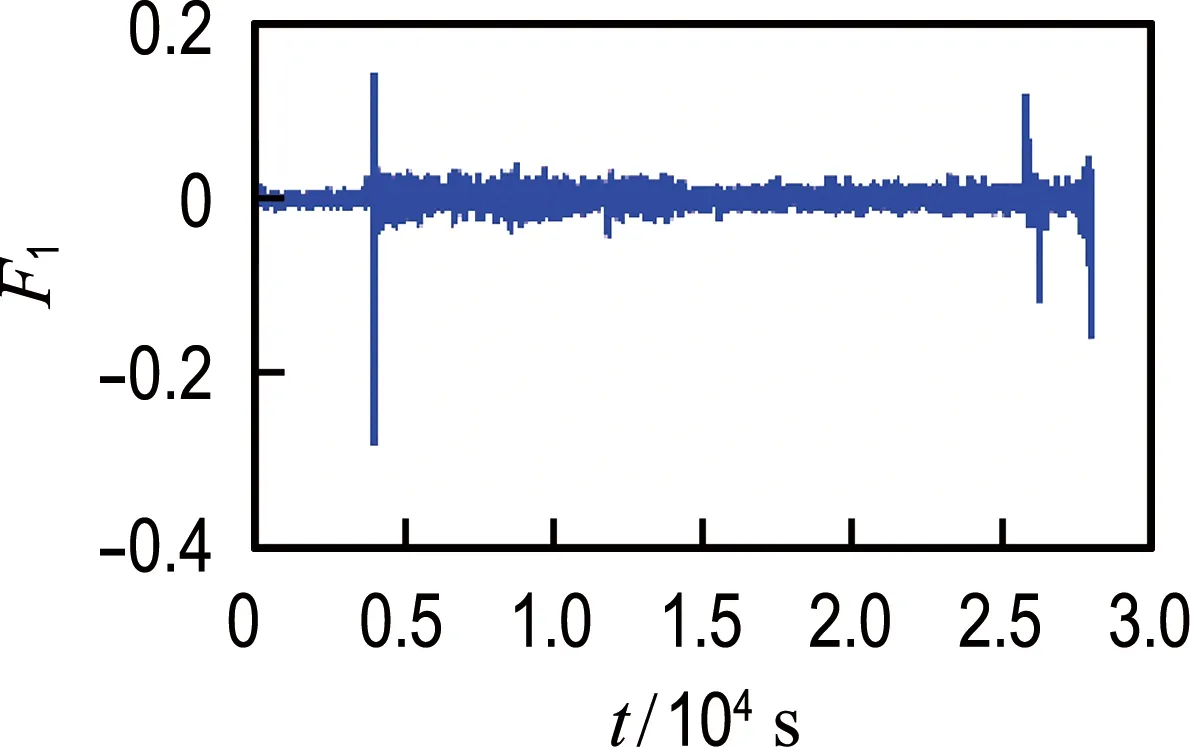
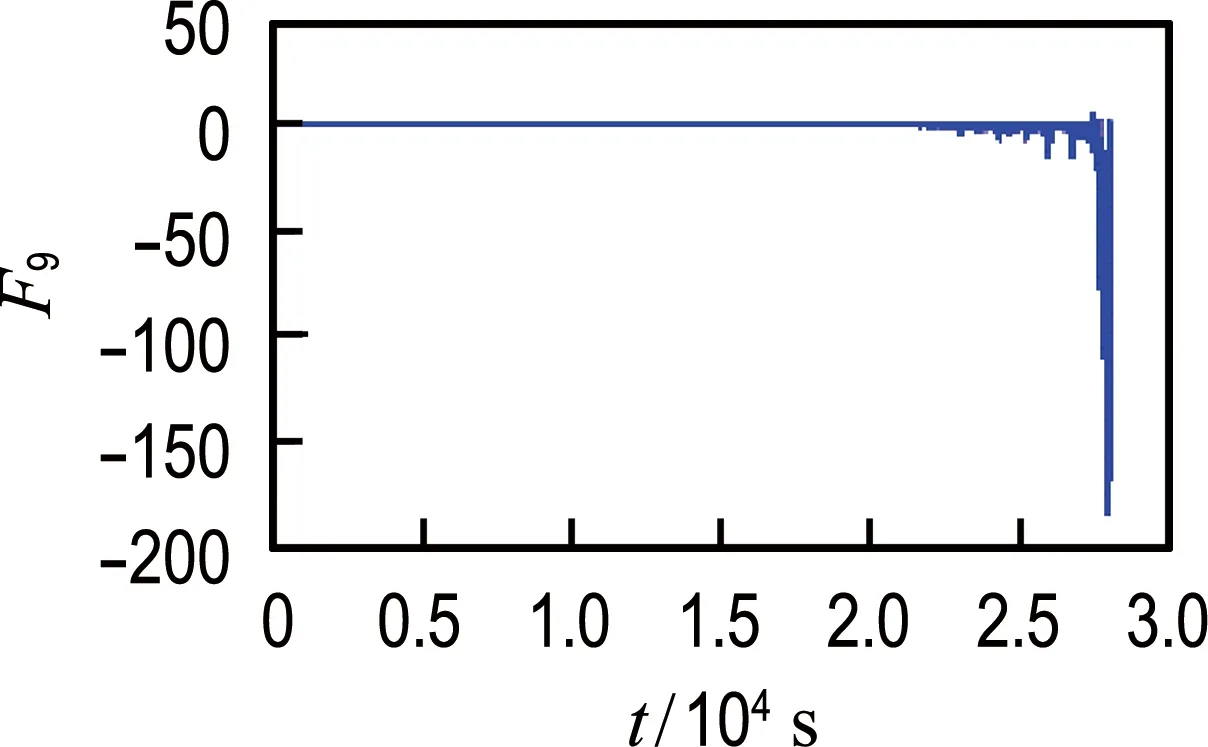
(b) 最差特征

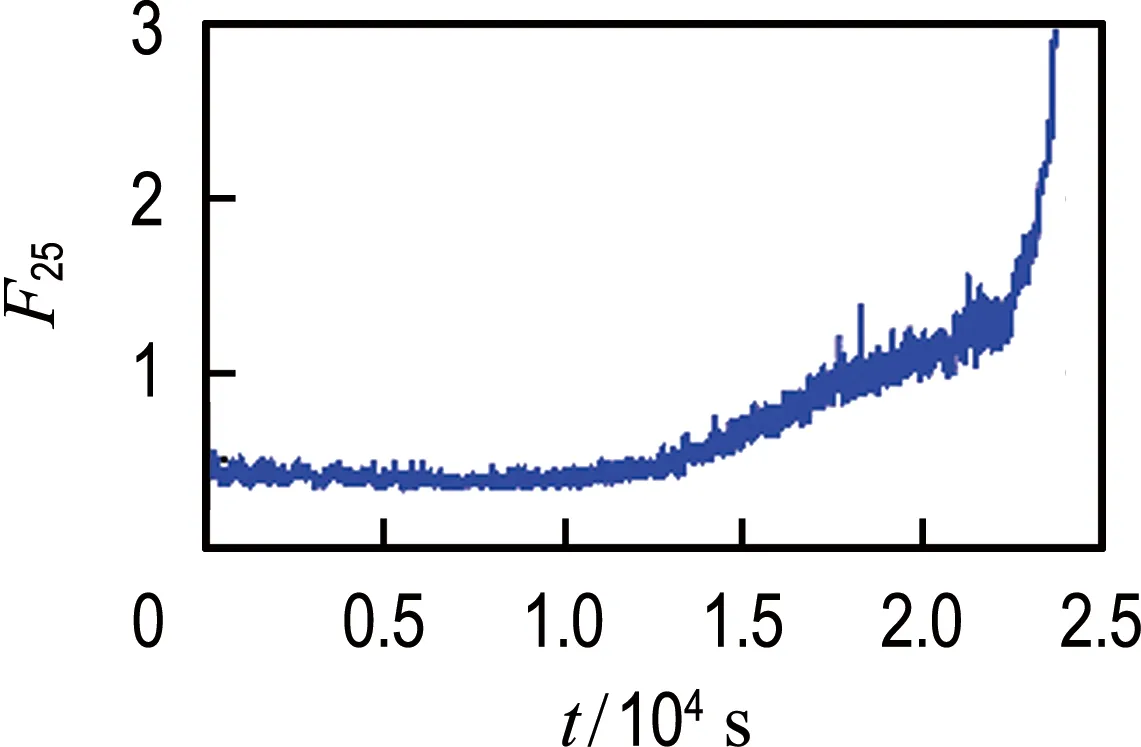
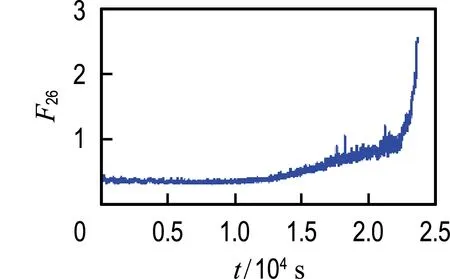
(a) 最优特征

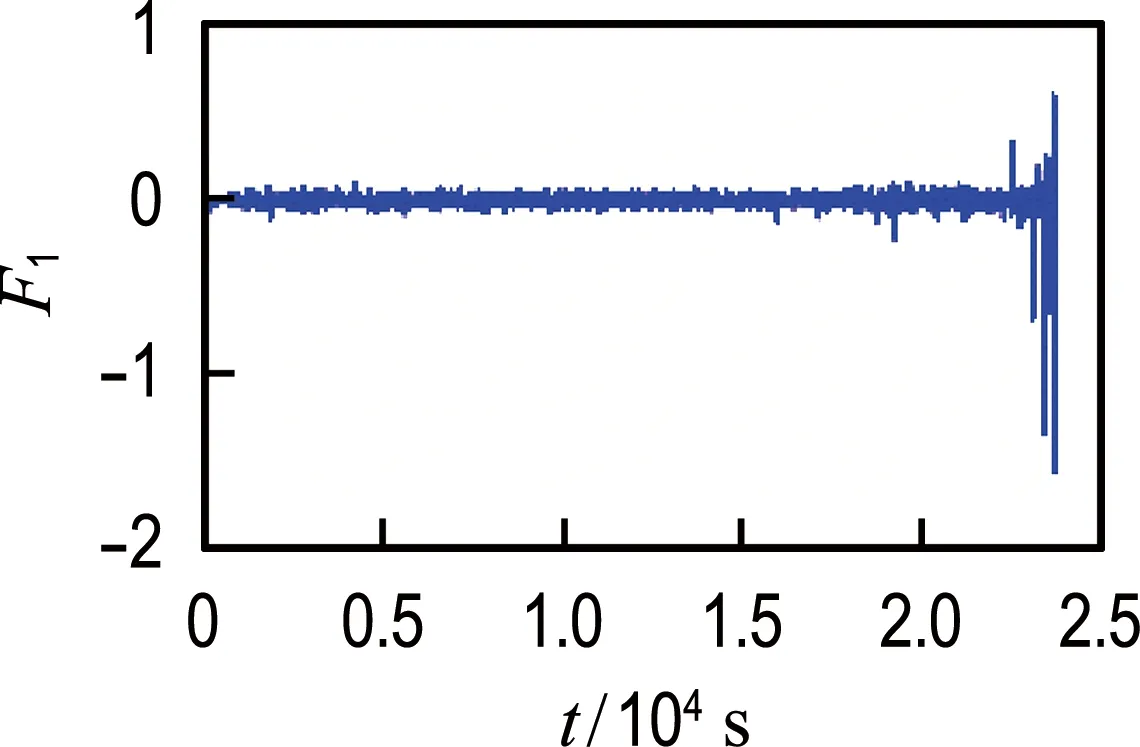
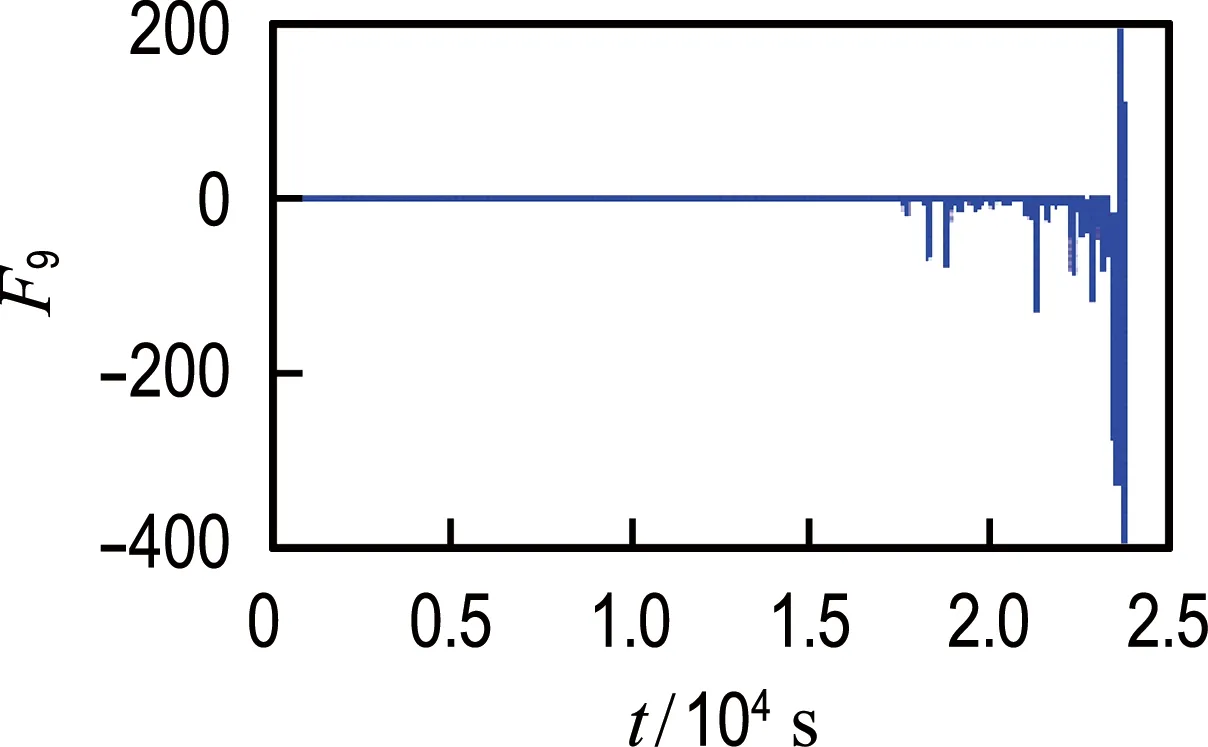
(b) 最差特征

表2 特征时间相关性对比

使用预处理后的退化指标，利用前文所述的寿命预测方法，对轴承剩余寿命进行预测．首先利用梯度值法检测轴承开始退化的时间，确定首次预测时刻．根据梯度值计算结果，将梯度值出现较大幅度增长后的值设置为阈值，可得轴承1梯度阈值为0.001 5，确定的TSP为第321 min，轴承2梯度阈值为0.000 8，确定的TSP为第 271 min，然后从TSP开始对轴承进行寿命预测．为证明本文提出的改进粒子滤波预测算法的优势，使用常规粒子滤波算法进行对比实验．

对于轴承1，首先使用轴承全寿命振动数据构建退化指标，然后确定了TSP为第321 min，即将前320 min的退化指标作为已知序列，将其代入状态转移方程，对模型中参数A和n进行非线性最小二乘拟合，得到模型参数的初始值．然后使用本文提出的改进粒子滤波算法对模型参数不断调整，使用的训练数据为前320 min的退化指标序列，待更新结束后，将最新的估计值作为模型参数，从第321 min起对轴承未来状态进行递推预测，从而得到轴承的剩余寿命估计．轴承2寿命预测过程同理．

图7和图8分别为轴承1和轴承2的预测结果．图7(a)和图8(a)为使用常规粒子滤波进行预测的结果，图7(b)和图8(b)为使用粒子群优化粒子滤波算法预测的结果．通过对比两图，直观上可以看出改进算法的预测值更趋近于真实值，并且剩余寿命分布的置信区间更为集中，说明改进算法的预测精度更高．

(a) PF预测结果

(b) PSO-PF预测结果

(a) PF预测结果

(b) PSO-PF预测结果

为量化说明改进算法的优势，使用平均相对误差(emap)、均方误差(erms)和剩余寿命概率分布的区间宽度3个指标对其进行评价．分析构建的退化指标，将失效阈值设为0.5，则可以根据下式计算轴承的剩余使用寿命(Nr)：

Nr=tpre-tFPT

(31)

式中：tpre为预测的失效时刻，tFPT为开始预测的时刻．

emap和erms的计算公式如下：

(32)

(33)

剩余寿命概率分布的区间宽度是通过计算剩余寿命分布的95%置信区间得到的，区间宽度越小，说明预测的概率分布越集中，预测结果越准确．

两种预测方法的量化对比结果如表3所示．从预测误差角度看，使用PSO-PF预测方法的平均相对误差和均方误差值都小于PF预测方法；并且从寿命分布来看，改进算法预测的寿命概率分布的区间宽度更小，说明预测效果更好．因此本文使用的改进粒子滤波算法能够有效地提高轴承寿命预测的精度．

表3 预测结果对比

5 结 语

为准确预测轴承剩余使用寿命，本文提出了一种粒子群优化粒子滤波的轴承寿命预测方法．首先，为精确预测轴承剩余寿命，需建立能够描绘轴承故障演化的退化指标．本文通过特征提取、优选、加权融合，获得了全面反映轴承故障发展的退化指标．并且通过自适应退化检测法得到首次预测时刻．最终使用粒子群优化粒子滤波预测方法，从检测到的首次预测时刻起对轴承进行寿命预测．从与常规粒子滤波方法的对比结果来看，本文提出的改进方法能够有效提升粒子滤波算法的估计精度，更准确地预测轴承剩余寿命．