密度分层液体晃荡非线性相互作用机理研究

薛 米 安， 罗 铆 钧， 苑 晓 丽

( 1.河海大学 海岸灾害及防护教育部重点实验室， 江苏 南京 210024；2.河海大学 港口海岸与近海工程学院， 江苏 南京 210024；3.河海大学 理学院， 江苏 南京 211100 )

0 引 言

分层液体晃荡是指两种或两种以上互不相溶的流体在容器内的受迫运动，其特点是同时存在自由表面和密度界面．单层液体晃荡的研究已被广泛报道，Abramson[1]采用线性势流理论研究了柱形和球形容器内的液体晃荡，特别是液体动压对液舱内部结构的影响．Faltisen等[2]在Sloshing一书中对液体晃荡动力学做出了系统深入的研究．事实上，分层液体晃荡也是一种常见的现象[1]，如海洋平台上的油水分离器等．对密度分层晃荡的探索主要有理论研究[1-4]、数值研究[5-6]和实验研究[7]．沈国光等[8]、梁启智等[9]分别给出了两层不同密度液体在矩形及圆柱形容器内的解析解．刘东喜等[10]基于CLSVOF方法数值研究了两层液体晃荡，表明CLSVOF方法能够准确预测自由表面和油水界面随时间的变化．Xue等[11]基于改进流体体积法模拟了具有自由液面的油-水二维分层液体晃荡并进行了实验验证．Molin等[12]通过实验和数值模拟研究了含自由液面的三层流体晃荡，发现在简谐激励下运动幅度增加时由于界面处非线性相互作用的影响，响应幅度算子RAO的峰值趋向更高或更低频率的方向移动．

傅里叶变换[11，13]是一种在时域或频域内分析数据的全局变换方法，但是它不能同时分析两个域中的数据．小波变换是继承和发展了短时傅里叶变换的局部化思想，能够分析时变信号的局部特征．对液体晃荡过程中各物理量的变化进行小波变换能够分析晃荡系统能量的频率分布．Jiang等[14]对弹性液舱晃荡特性试验数据进行了Morlet小波变换，表明晃荡能量主要集中在外激励频率附近，并在剧烈条件下扩展到高频，建议工程师要关注晃荡的一阶固有频率和脉冲峰值压力可能导致的结构损坏．Morlet小波变换作为新的分析工具，受到众多学者关注，例如，Ma等[15-16]利用Morlet小波变换分离二维入射波和反射波．

非线性是波浪的重要特征，可以表征波浪能量在不同频率之间的传递[17]．非线性波-波相互作用的特征在于二次相位耦合，而小波二阶相关谱是分析波的二次非线性相互作用的强有力的工具，它可以提供相位耦合的相对程度[18]．Dong等[19]利用小波二阶相关谱研究了不规则波浪在曲线形潜堤上传播时的非线性特性，并与傅里叶二阶相关谱对比发现小波二阶相关谱具有更大的有效自由度，可以用来检测短时间序列的二次相位耦合．由于小波二阶相关谱可以提供相位耦合的时间函数，可利用其研究物理量的频率分布随时间变化的规律．

本文首先介绍液体晃荡试验装置、分层液体晃荡色散方程、Morlet小波和小波二阶相关谱方法．其次讨论基于快速傅里叶变换和Morlet小波变换的试验数据结果以及小波二阶相关谱在非线性特征分析中的应用．最后利用分层液体晃荡界面内波和晃荡压力数据分析分层液体晃荡非线性相互作用．

1 液体晃荡试验装置

1.1 振动台

本试验是在河海大学振动测试与液舱晃荡实验室的六自由度液舱晃荡试验平台上开展的．试验中，压力传感器、波高仪、摄像机分别被用于测量液体在晃荡过程中的冲击压强、界面波波高和液体运动图像随时间变化的规律．液舱固定在液体晃荡整体水动力测量仪面板上，测量仪面板通过力传感器与振动台相连，液舱与振动台无相对位移，固定在面板上的力传感器可以测量运动的流体对液舱内壁的水动力．

该试验装置可用于水平激励下的液体晃荡特性研究，通过计算机控制软件对振动台输入以下运动信息：

x=Asinωt

(1)

式中：运动振幅A=10 mm．

1.2 液舱模型及测量仪器布置

试验中液舱的长度L=0.51 m，宽度W=0.15 m，高度H=0.47 m．液舱由透明有机玻璃板制作而成，厚度为6 mm，可假定为刚性材料．2只浪高仪分别布置在距离矩形液舱左右壁面18 mm 位置处并固定在液舱上，6只压力传感器P1、P2、P3、P4、P5、P6依次安装在液舱左壁离舱底11.0、30.5、52.0、70.2、90.2、105.0 mm处．试验液体采用自来水和0#柴油．

1.3 试验工况

如图1所示，考虑一个二维矩形液舱，在x向长度为a，其内部置入密度和深度分别为ρ1、ρ2和h1、h2的两层互不相溶流体．在理想流体和微幅波理论假定下，根据速度势描述的方程推导出固有频率ωn与几何尺度及密度之间的色散关系为[8]

(2)

式中

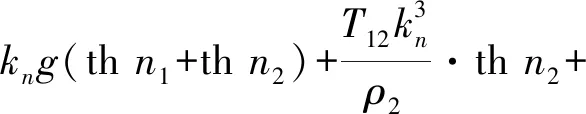
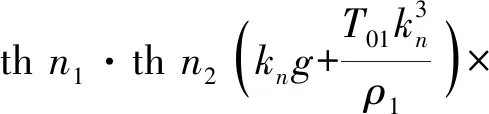
γn=2(1+R12thn1·thn2)

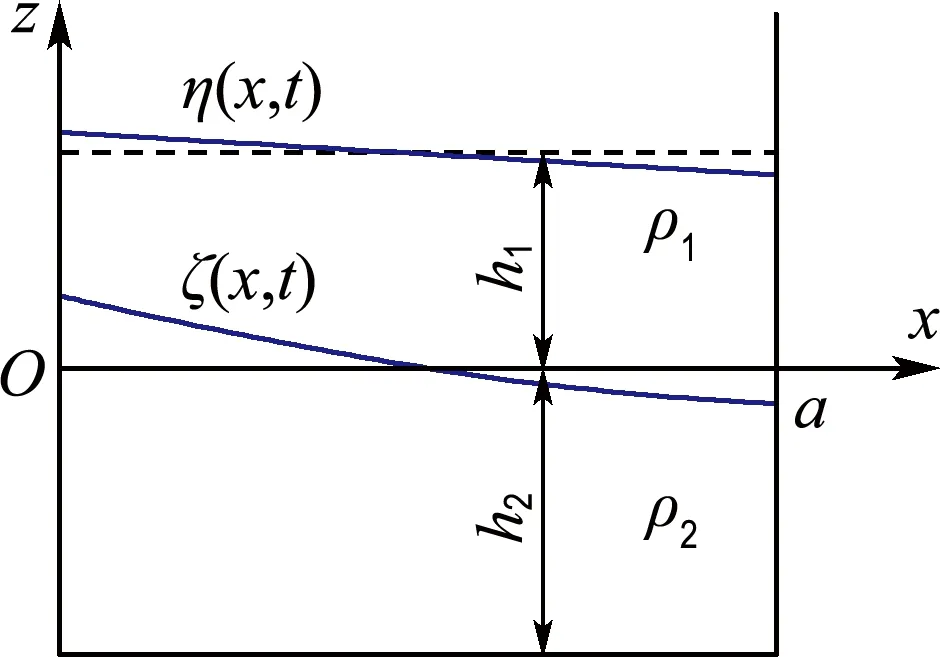
图1 二维矩形液舱分层液体晃荡示意图

研究中液体总深度为0.12 m，液体深度比为1.0(两种液体的深度均为0.06 m)，则由式(2)计算出一阶固有频率为0.97 Hz，试验中每次液舱运动时长约为100 s．考虑到外激励频率接近分层液体固有频率时，会发生强非线性相互作用，因此选取外激励频率为0.93f0、1.00f0、1.07f0，其中f0为该分层液体系统的固有频率0.97 Hz．同时为了研究分层液体晃荡非线性相互作用较弱的情况，选取外激励频率为远离分层液体系统固有频率的低频0.70 Hz和高频1.40 Hz．

2 Morlet小波变换

2.1 小波能谱

小波变换继承和发展了短时傅里叶变换的局部化思想，能够分析时变信号的局部特征[20]，也可以呈现物理量的时间-频率分布．对液体晃荡过程中各物理量的变化进行小波变换能够分析晃荡系统能量的频率分布．基于小波变换的结果WT(s，t)定义小波能谱[18]：

(3)

式中：s为尺度，t为时间．

2.2 Morlet小波

Morlet小波在时域和频域都有很好的局部性[21]，并且被广泛应用于小波变换的母函数，其公式为[18]

(4)

式中：ω0是中心角频率．

2.3 小波二阶相关谱

量纲一化的小波二阶相关谱的定义为[22]

(5)

式中：下标w为小波变换的结果；T为分析信号的时长；fi为频率，若满足f1±f2=f3，则bw为一个大于0的数．bw的值介于0～1，bw等于0说明3个频率的组成波之间没有相互作用，bw等于1说明3个频率的组成波之间完全相关[14]．因此，可以通过bw来判断组成波之间非线性相互作用强度的强弱．

3 结果与讨论

3.1 界面波波高的小波分析

选取5个工况中左侧波高仪的数据，界面波波高随时间变化曲线如图2所示．分层液体刚开始晃荡时，外激励频率从0突增到工况频率，系统快速获得能量，界面波波形增大且不对称．波形的变化主要是由界面波各频率成分的非线性相互作用产生的高次谐波所致．因此，可以从界面波形图中看到运动初始时系统非线性相互作用较强．

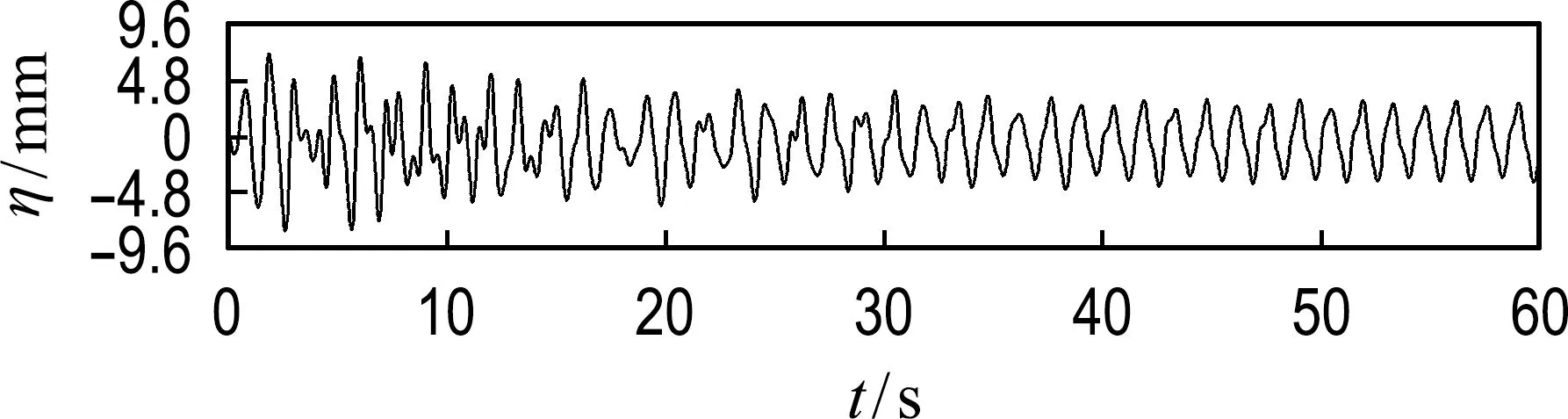
(a) f=0.70 Hz

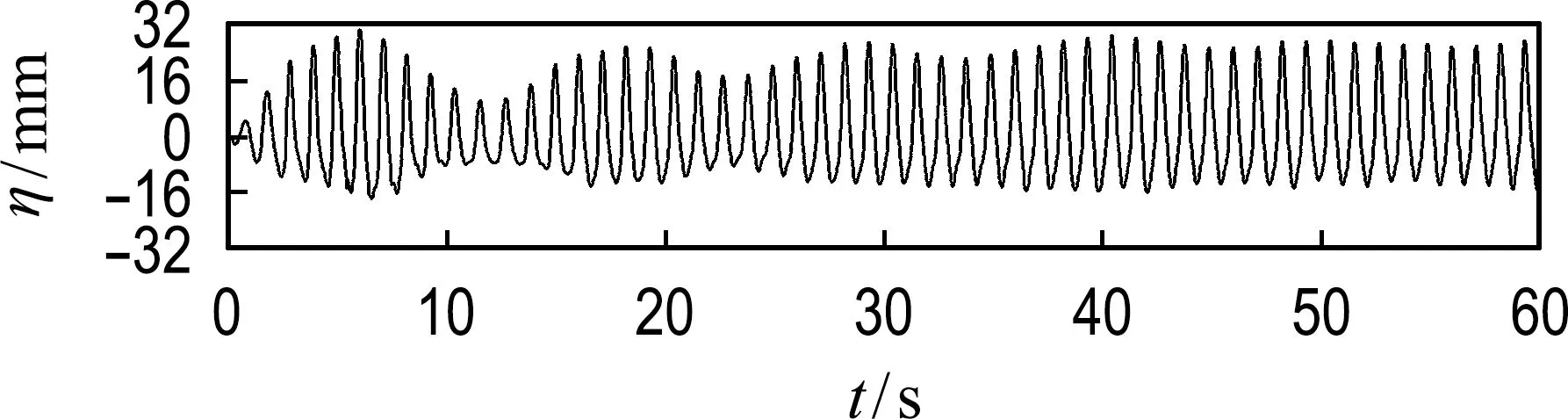
(b) f=0.90 Hz

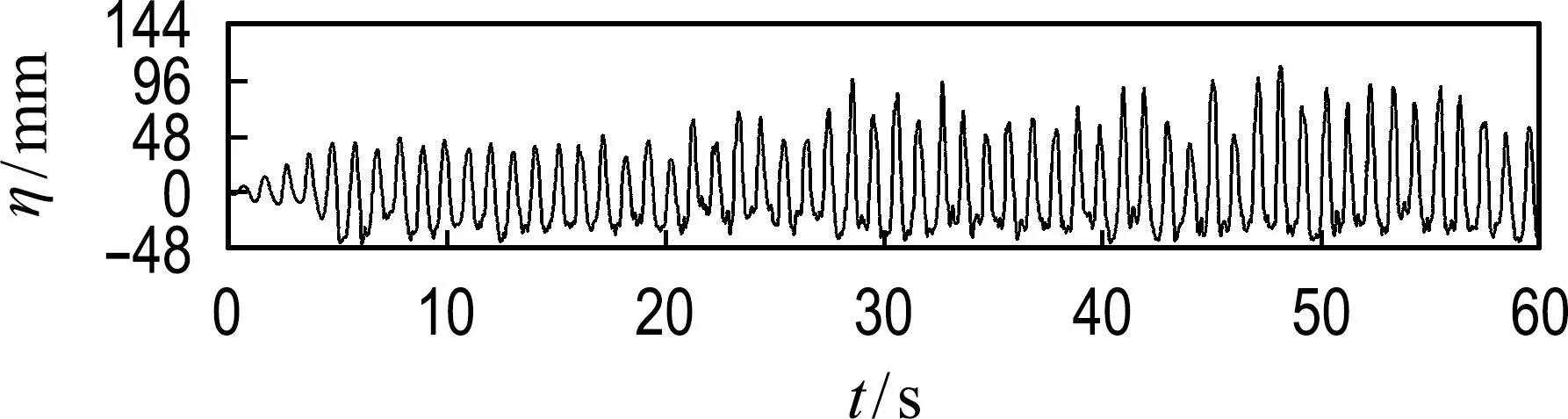
(c) f=0.97 Hz

(d) f=1.03 Hz

(e) f=1.40 Hz

分布于不同频率的界面波能量可以很清楚地从快速傅里叶变换中观察到，如图3所示．当外激励频率等于固有频率时，界面波所获得的能量最大，并且由非线性相互作用产生频率为1.94 Hz的界面波．当外激励频率接近固有频率时，界面波获得的能量相较于共振情况减小，但非线性相互作用较强．当外激励频率远离理论固有频率时，系统获得的能量较少，且非线性相互作用也较弱，能量谱中能量的转移是由于组成波之间的非线性相互作用所致，如在低频工况下，频率为0.70 Hz(外激励频率)的界面波和频率为0.97 Hz(固有频率)的界面波发生非线性相互作用产生了频率为1.67 Hz的界面波；在高频工况下，频率为1.40 Hz(外激励频率)的界面波和频率为0.96 Hz(固有频率)的界面波发生非线性相互作用产生了频率为2.36 Hz的界面波，但获得的能量低于频率等于外激励频率的界面波自身之间发生非线性相互作用产生频率为2.80 Hz的界面波所获得的能量．

虽然可以从快速傅里叶变换中了解到主要频率成分的界面波参与了非线性相互作用，但是它们在时间序列中哪个时间段发生是未知的．因此基于Morlet小波变换研究了其时频特性和统计分布，如图3所示．当外激励频率为理论固有频率时(图3(c))，在时间段0～2.7 s，界面波的频率主要为外激励频率，在2.7 s之后，由非线性相互作用产生频率为1.94 Hz的界面波，并且随着时间的推移，频率为1.94 Hz的界面波所获得的能量越来越多．当外激励频率为0.90 Hz接近固有频率时(图3(b))，在时间段0～10.0 s发生的非线性相互作用强于其他时间段，并且从界面波波高随时间变化曲线(图2(b))中可以看到包络现象，而每个包络周期结束时，是非线性相互作用最弱的时间段．当外激励频率为1.03 Hz接近固有频率时(图3(d))，可以看到在整个运动时间段内均发生了非线性相互作用．当外激励频率远离理论固有频率时(图3(a)和图3(e))，界面波之间在运动初始时间段发生较强非线性相互作用，但随着运动时间的推移，非线性相互作用逐渐减弱至一定程度并持续至运动结束．此外，通过Morlet小波变换还可以了解到界面波形成的最大波高发生在强非线性相互作用的时间段内，如外激励频率远离理论固有频率(图3(a)和图3(e))时，界面波在运动初始时间段内发生强非线性相互作用，此时产生的界面波波高值最大(图2(a)和图2(e))；外激励频率为理论固有频率(图3(c))时，界面波随着运动时间的不断推移，其非线性相互作用也逐渐增强，此时界面波波高的最大值产生在非线性相互作用最强的时间段内(图2(c))．

(a) f=0.70 Hz

(b) f=0.90 Hz

(c) f=0.97 Hz

(e) f=1.40 Hz

3.2 晃荡压力的小波分析

通过快速傅里叶变换和Morlet小波变换对界面波的比较分析，可以更深入地了解响应系统与外激励之间的联系，因此采用同样的方法对分层液体晃荡压力进行分析，压力随时间变化如图4所示．图4(a)～4(c)分别为外激励频率0.70、0.97和1.40 Hz，P1测点；图4(d)～4(f)分别为外激励频率0.70、0.97和1.40 Hz，P6测点．由图4可知，当外激励频率等于理论固有频率时产生的晃荡压力大于当外激励频率远离理论固有频率时产生的压力．

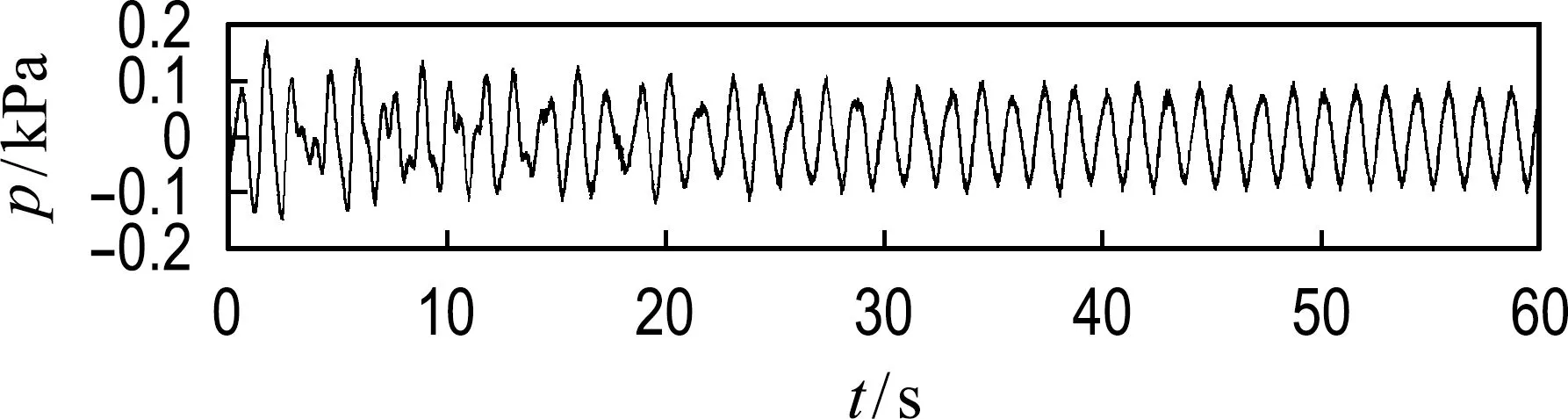
(a) P1测点，f=0.70 Hz

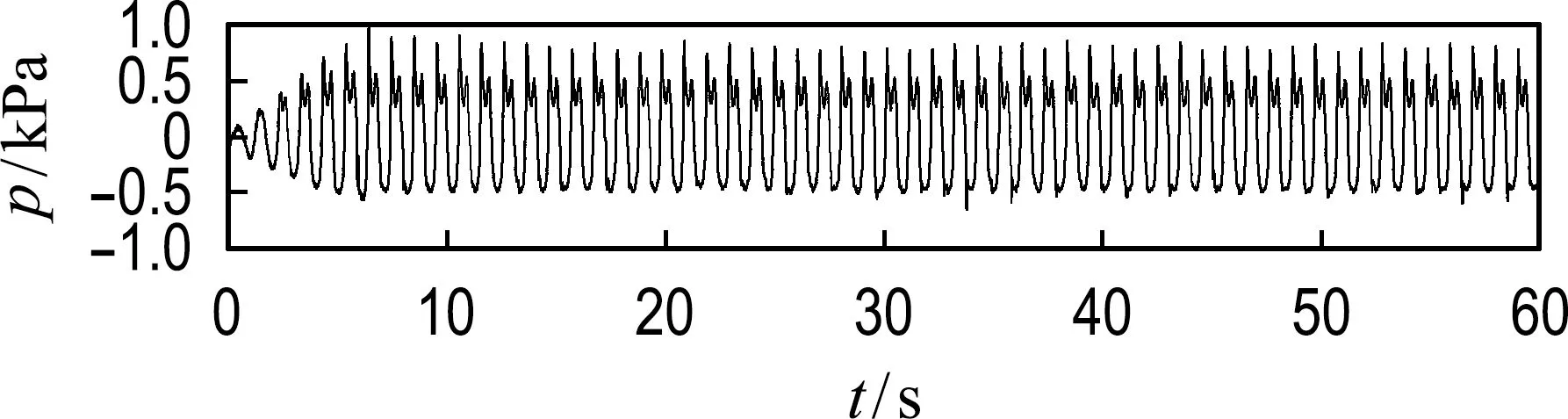
(b) P1测点，f=0.97 Hz

(c) P1测点，f=1.40 Hz

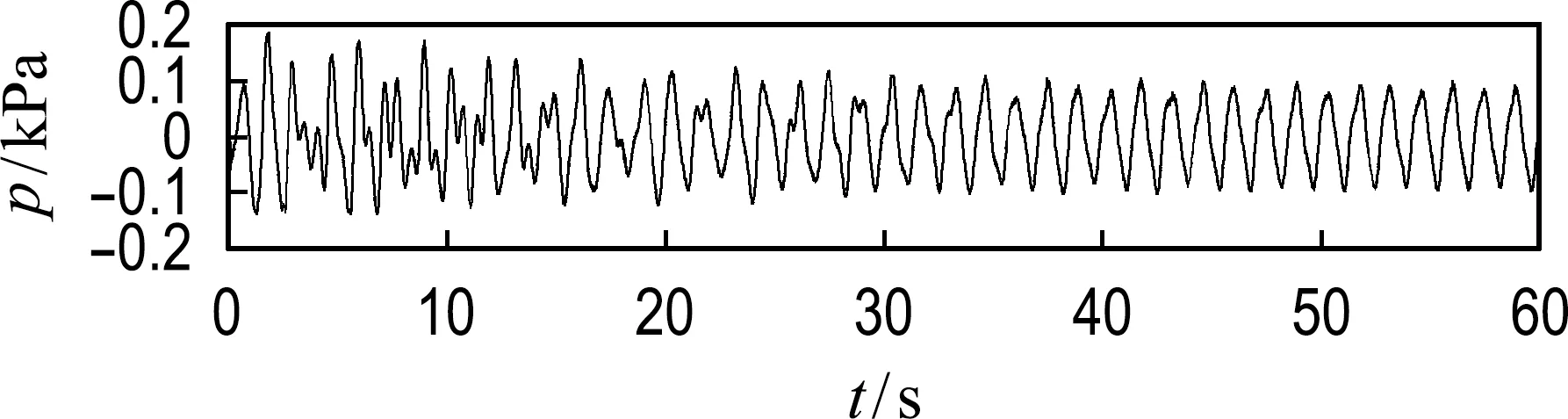
(d) P6测点，f=0.70 Hz

(e) P6测点，f=0.97 Hz

(f) P6测点，f=1.40 Hz

图5显示了晃荡压力时间序列的快速傅里叶变换和Morlet小波变换．在晃荡压力的快速傅里叶变换中，当外激励频率为0.70 Hz时，P6测点各个压力频率成分的振幅值均大于P1测点各个压力频率成分的振幅值，值得注意的是P6测点位于自由表面波和界面波之间，P1测点位于界面波之下且接近液舱底部，这说明自由表面波和界面波在P6测点处产生更大的压力；当外激励频率为0.97 Hz(理论固有频率)时，发现压力频率成分为3倍外激励频率的振幅值大于压力频率成分为2倍外激励频率的振幅值，相同的，P6测点各个压力频率成分的振幅值均大于P1测点各个压力频率成分的振幅值，且P6测点压力频率成分中4倍外激励频率的压力振幅值大于压力频率成分为2倍外激励频率的压力振幅值；当外激励频率为1.40 Hz 时，P1测点压力频率成分中含有外激励频率的倍频，而P6测点中含有一阶固有频率和外激励频率耦合成的频率，这表明作用在液舱壁面上的压力特征是不同的．

(a) P1测点，f=0.70 Hz

(b) P1测点，f=0.97 Hz

(c) P1测点，f=1.40 Hz

(d) P6测点，f=0.70 Hz

(e) P6测点，f=0.97 Hz

(f) P6测点，f=1.40 Hz

Morlet小波变换给出了晃荡压力频率分布随时间的变化．当外激励频率为0.70 Hz时，与界面波序列相对应，在运动初始时间段有着较强的非线性相互作用，使得晃荡压力中含有1.67 Hz频率成分，当运动达到稳态时，非线性相互作用减弱；当外激励频率为0.97 Hz(理论固有频率)时，可以看到分层液体晃荡在全时间段内发生强非线性相互作用，大量能量传递至频率成分等于3倍外激励频率的界面波，同时，P6测点压力非线性相互作用也强于P1测点压力非线性相互作用；当外激励频率为1.40 Hz时，在运动初始时间段有着较强的非线性相互作用，之后的时间段内非线性相互作用较弱．综上可知通过Morlet小波变换，可以揭示最大压力发生在非线性相互作用最强的时间段内．

3.3 基于小波二阶相关谱的非线性相互作用程度分析

快速傅里叶变换可以给出时间全局上的物理量频率分布，Morlet小波变换可以给出随时间变化的物理量频率分布，但是由于非线性相互作用，这两种分析方法并不能具体描述不同或相同频率成分之间的非线性相互作用程度．通过小波二阶相关谱可以看出界面波序列的二阶耦合相关程度的大小，可用于研究分层液体晃荡界面波之间的二阶非线性相互作用．

图6所示的是5个工况下界面波(图2)的小波二阶相关谱．小波二阶相关谱的横纵坐标均为频率，由2.3可知，bw的值介于0～1，bw等于0说明3个频率的组成波之间没有相互作用，bw等于1说明3个频率的组成波之间完全相关[14]．小波二阶相关谱显示当外激励频率为0.70 Hz时(图6(a))，有频率为0.70 Hz和0.97 Hz的界面波通过非线性相互作用产生了频率为1.67 Hz的界面波，有频率为0.70 Hz和1.67 Hz的界面波通过非线性相互作用产生了频率为2.37 Hz的界面波；当外激励频率为0.90 Hz时(图6(b))，有频率为0.90 Hz的界面波之间通过非线性相互作用产生了频率为1.80 Hz的界面波，有频率为0.90 Hz和1.80 Hz的界面波通过非线性相互作用产生了频率为2.70 Hz的界面波；当外激励频率为0.97 Hz时(图6(c))，有频率为0.97 Hz之间的界面波通过非线性相互作用产生了频率为1.94 Hz的界面波；当外激励频率为1.03 Hz时(图6(d))，有频率为1.03 Hz的界面波之间通过非线性相互作用产生了频率为2.06 Hz的界面波；当外激励频率为1.40 Hz时(图6(e))，有频率为0.96 Hz和1.40 Hz的界面波通过非线性相互作用产生了频率为2.36 Hz的界面波，有频率为1.40 Hz的界面波之间通过非线性相互作用产生了频率为2.80 Hz的界面波．

同时，从图6中观察到非线性相互作用程度最强的为外激励频率接近理论固有频率(图6(b)、(c)和(d))，其程度在小波二阶相关谱中接近1．小波二阶相关谱越接近1，说明非线性相互作用程度越强．不同或相同频率的界面波之间发生非线性相互作用产生叠加频率的界面波，且所产生的界面波能量来源是发生非线性相互作用的界面波．

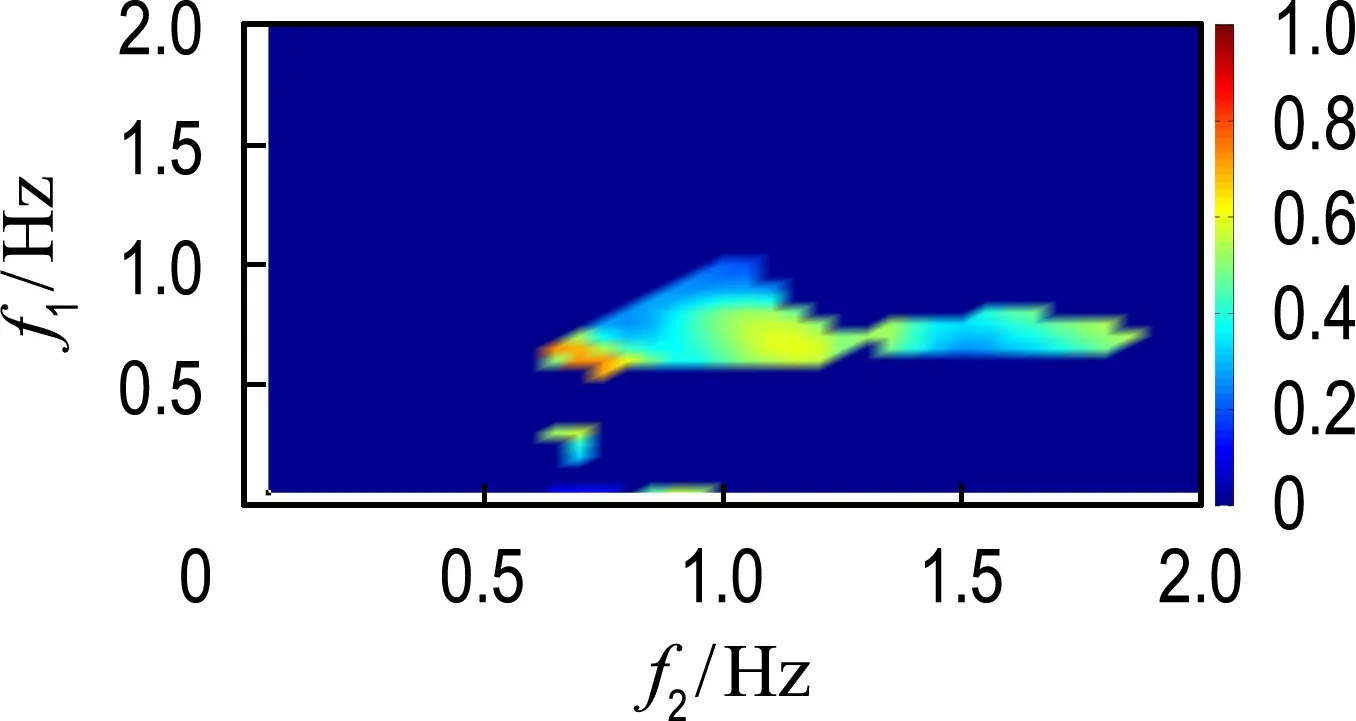
(a) f=0.70 Hz

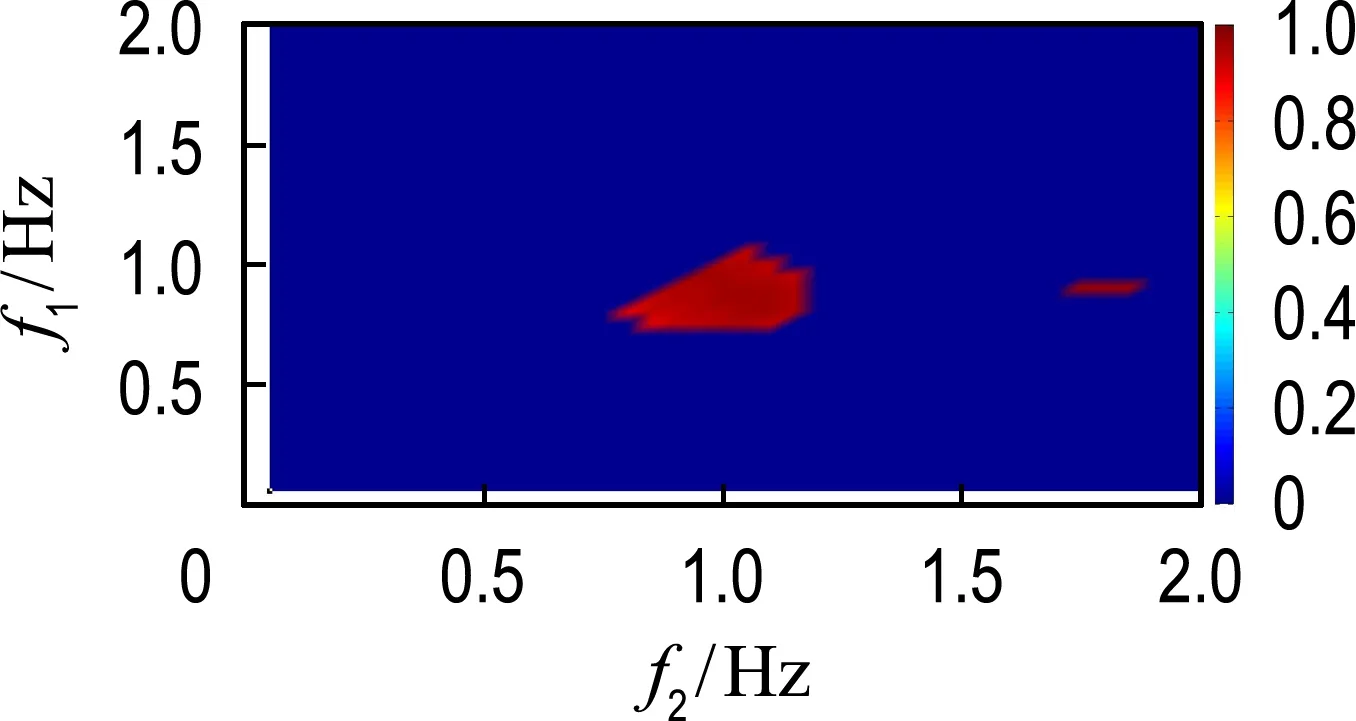
(b) f=0.90 Hz

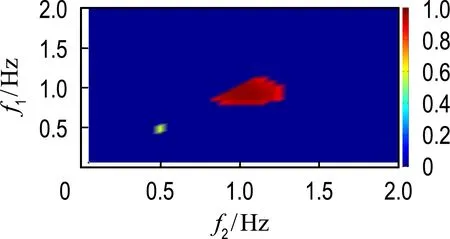
(c) f=0.97 Hz

(d) f=1.03 Hz

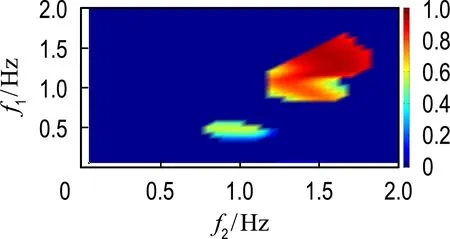
(e) f=1.40 Hz

4 结 论

(1)快速傅里叶变换可以给出时间全局上的物理量频率分布，通过快速傅里叶变换对分层液体晃荡界面波和晃荡压力进行了分析，结果表明频率成分等于外激励频率所获得的能量最大，并且当外激励频率从高频或低频趋近于固有频率时，界面波波高和晃荡压力都逐渐增大，非线性相互作用程度增强．

(2)Morlet小波变换可以给出随时间变化的物理量频率分布，通过Morlet小波变换对分层液体晃荡界面波和晃荡压力进行了分析．结果表明界面波最大波高和最大晃荡压力发生在强非线性相互作用的时间段内，当外激励频率远离理论固有频率时，只在分层液体晃荡初始时间段内发生较强的非线性相互作用；当外激励频率等于理论固有频率时，非线性相互作用程度随着时间推移越来越强．从Morlet小波变换结果可知液体晃荡吸收的能量主要集中在外激励频率附近．

(3)小波二阶相关谱可以解释Morlet小波变换中出现的频率变化．非线性相互作用程度最强的工况为外激励频率等于理论固有频率，其程度在小波二阶相关谱中接近1．小波二阶相关谱越接近1，说明非线性相互作用程度越强．当外激励频率远离理论固有频率时，界面波频率成分之间也有相当程度的非线性相互作用(bw>0.5)．