考虑层间接触状态的沥青路面疲劳性能预估

李 玲， 张 玉， 张 勇 博

( 1.新疆大学 建筑工程学院， 新疆 乌鲁木齐 830047；2.同济大学 道路与交通工程教育部重点实验室， 上海 201804 )

0 引 言

沥青混凝土路面因其行车舒适、易于养护等诸多优点得到广泛应用．然而，急剧增加的交通荷载和复杂气候环境致使沥青路面病害尤其是疲劳开裂日益凸显，严重影响到沥青路面耐久性．路面疲劳寿命与荷载、环境、结构层组成、层间处置技术等密切相关，且层间接触状态对其影响显著．研究表明：在整个寿命周期内，层间性状的不断演化和劣化是加剧沥青路面疲劳损伤和永久变形等病害的主要原因[1]．层间接触状态的变化将导致路面结构应力重分布，随着层间黏结力的下降，沥青路面疲劳寿命快速下降[2]．目前对于考虑层间接触状态的沥青路面力学响应与其疲劳特性尚未得到有效结合，因此，迫切需要针对沥青路面层间接触状态，提出准确合理的评价指标与评判标准，从而构建科学的评价体系．

道路疲劳破坏研究起始于材料疲劳破坏研究，研究重点是如何科学、合理地确定疲劳模型[3-9]．陈少幸等[10]根据加速加载试验，总结了面层模量和层底应变的演变规律．孙志林等[11]通过构建沥青路面结构有限元模型对结构损伤、水平拉应力在温度、荷载作用下沥青路面裂纹形成过程进行分析．可以看出，为提高路面承载能力、服务性能与耐久性，并减小运营期间养护费用，路面应具有良好层间黏结特性．

本文对沥青路面疲劳性能预估模型进行分析，通过数值模拟与理论分析确定沥青层模量、基层模量、层间接触状态与荷载等结构层状况参数为核心预估变量，构建考虑层间接触状态的沥青路面疲劳性能预估模型．由于半刚性基层沥青路面面层与基层是两个完全不同材料的界面，本身存在接触问题，材料模量不协调、刚度差异大，为层间最薄弱部位，因此本文重点针对此路面结构开展研究．

1 疲劳寿命预估模型

目前国际上推荐采用的疲劳开裂破坏模型种类繁多，Finn等[12]认为沥青混合料的疲劳开裂与应变水平、劲度模量均有关，其主要形式为[13]

(1)

式中：Nf为荷载作用次数；εt为所施加拉应变；Smix为混合料初始劲度模量；k1、k2和k3为试验确定的参数．

沥青协会(AI)根据Finn等提出的方程，综合考虑Pell等[14]建议的沥青混合料特性修正系数，结合现场观测，确定疲劳设计方程如下：

(2)

式中：E为沥青材料动态回弹模量，6.9 kPa；Va为材料空隙率，%；Vb为有效沥青体积含量，%．

壳牌(SHELL)设计法提出：不同应力状态与不同厚度的沥青路面疲劳损坏机理不同，鉴于此，针对不同厚度沥青层分别提出了常应变与常应力两类疲劳设计方程[15]，如式(3)、(4)所示．

常应变(沥青层较厚时推荐采用)：

Nf=Af×(0.17×Ip-0.008 5×Ip×Vb+0.045 4×

(3)

常应力(沥青层较薄时推荐采用)：

Nf=Af×(0.025 2×Ip-0.001 26×Ip×Vb+

(4)

式中：Af为现场修正因子，默认取1.0；Ip为沥青针入度指数．

国内外研究人员将AI法与SHELL法疲劳寿命预估模型进行比较，经过大量计算验证，发现AI法更具普遍性，本文采用此模型作为疲劳开裂形式．

沥青混合料空隙率设为5%，有效沥青体积含量为11%[16]．为与我国现行沥青路面设计规范[17]中参数相统一，本文采用静态模量作为疲劳开裂破坏准则中参数．研究表明：静、动抗压回弹模量之间符合动态模量为1.45～1.55倍静态模量[18-19]，本文选择1.5进行计算．将各参数代入式(2)，得到本文确立的疲劳开裂破坏准则如下：

(5)

式中：E*为沥青材料静态回弹模量，MPa．

2 小尺度动态响应试验

目前对路面结构层间接触状态的试验分析主要分为即时接触效应分析和接触状态演变分析两类．对接触效应的分析，国际上主要以静态或动态剪切试验为主．本文建议通过多层成型车辙板进行小尺度动态响应试验，可通过控制黏层油种类及用量、各层材料组成等人为处置，形成不同层间损伤行为的多层车辙板，在此基础上进一步探究层间接触状态．

2.1 原材料及级配组成

试验采用粗、细集料均为石灰岩，沥青选用克拉玛依90#基质沥青和阿拉尔市乳化沥青，经检测其各项技术指标均满足相应规范要求．参照相关规范[17]进行水稳层和沥青层设计，级配见表1、2．

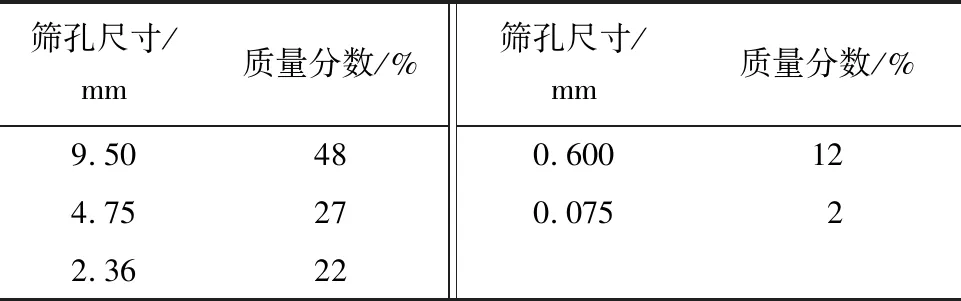
表1 骨架密实型水泥稳定类集料级配

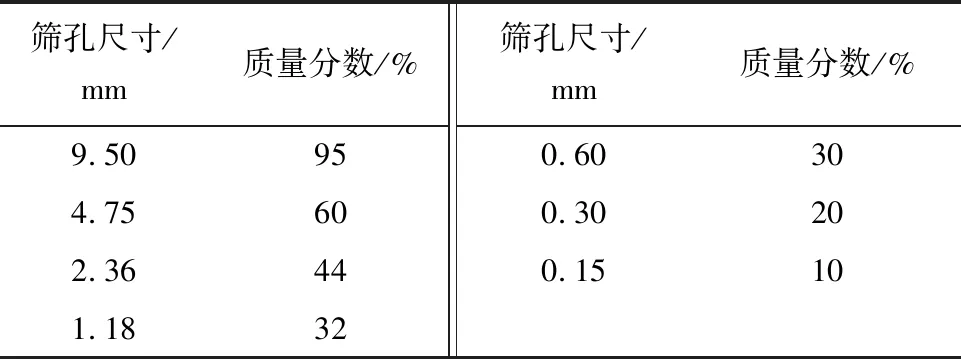
表2 AC-10混合料矿料级配组成

2.2 试件成型

成型复合车辙板时，首先利用300 mm×300 mm×50 mm的试验试模成型下层水稳板，待下层水稳板成型后约24 h进行拆模，养护7 d后清除其表面杂物，用砂纸打磨水稳板应变片布设位置(沿应变片长度方向)后开始布设应变片并对每个应变片进行编号．布设完成后用环氧树脂进行保护，常温下静置24 h．将水稳板置于300 mm×300 mm×100 mm的试验试模底部并在水稳板上洒铺乳化沥青黏层油，以其为底，加铺上层300 mm×300 mm×50 mm的沥青混凝土车辙板，模拟分层施工碾压工艺．其中，透层油洒铺量为0.4 L/m2[18]，成型后充分冷却约24 h后拆模．

2.3 应变片布设及采集结果

利用LHPL-6沥青混合料材料性能试验系统对复合车辙板施加荷载，整个试验过程为常温，具体按照规程[19]中车辙试验进行．车辙试验轮碾位置和应变片具体布设详见图1．

(a) 车辙位置图

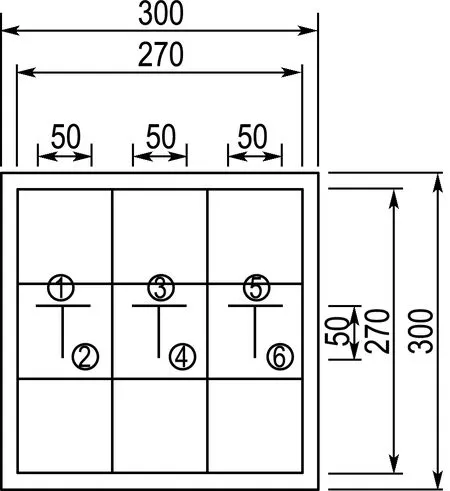
(b) 应变片布设图

试验采用DH5925N便携式动态信号测试分析系统(见图2)采集车辙试验下复合车辙板层间动态应变，采集频率为20 Hz，应变片与采集通道间的桥路连接为1/4桥．

图2 便携式动态信号测试分析系统

在动荷载作用下，不同位置处应变有所不同，但其反映出来的整个响应过程具有很多共同特征．试验过程中⑤号应变片损坏，鉴于①、②和⑤、⑥对称，数据采集时以①、②、③、④号应变片作为有效数据．图3为车辙试验轮碾行走过程中动态采集系统采集的应变数据．

从图3可以观察出：

(1)不同位置处动态应变随轮碾移动的变化趋势较为一致，均出现拉压应变交替现象．

(2)③号较①号以及④号较②号均有滞后现象，动态应变大小受轮碾位置影响．

(3)通过应变数据可以明显看出，③号应变片位置处动态应变持续高于其他位置，说明③号位置距离最不利作用位置最近．

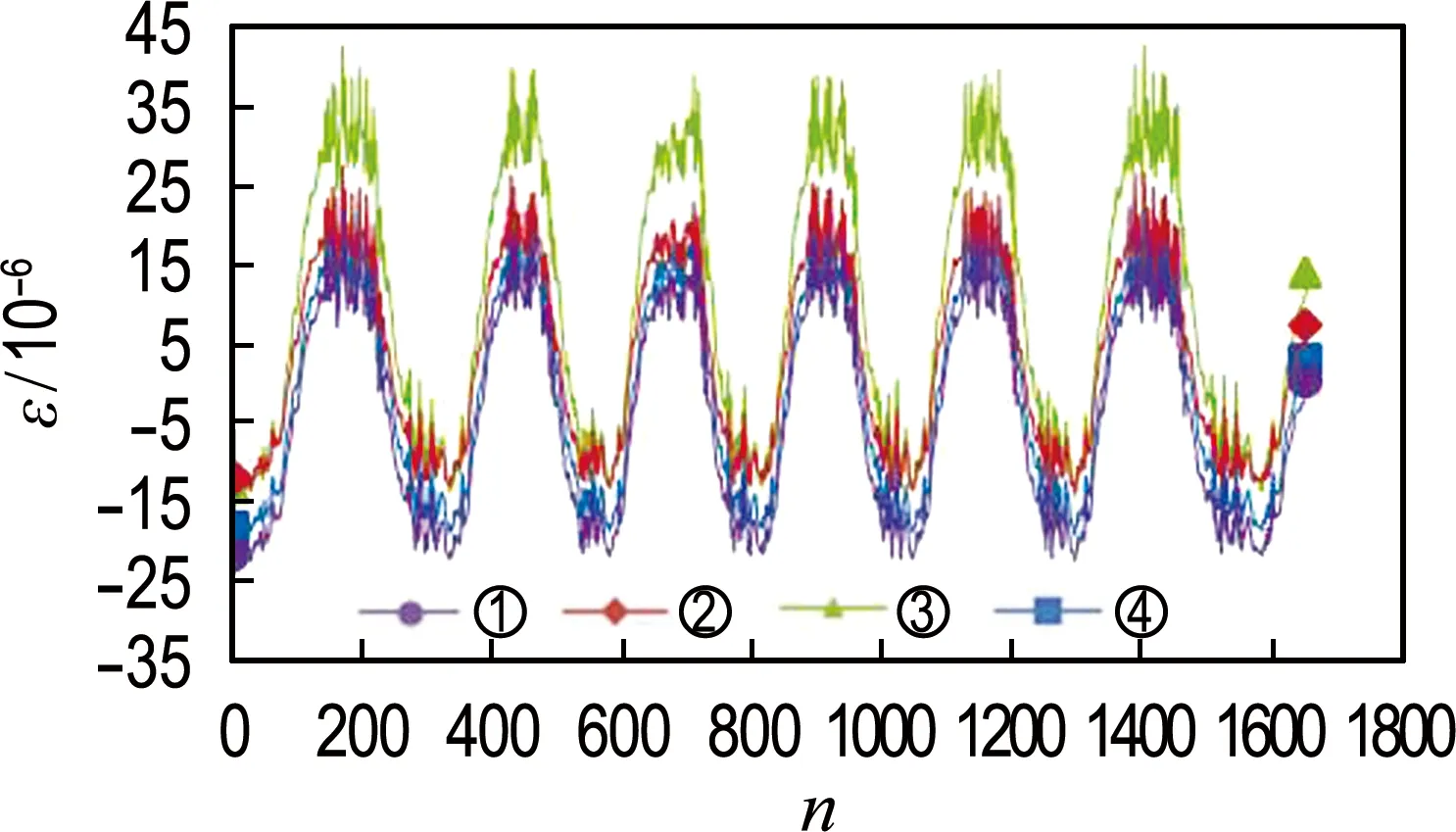
图3 小尺度动态应变时程曲线

2.4 试验可靠性验证

采用ABAQUS建立车辙试验等尺度模型，如图4所示．鉴于实际车辙中试件成型完成后即进行试验，层间接触良好，在有限元模拟中采用“Tie”模拟基-面层间为完全连续状态．

图4 车辙试验模型网格划分

有限元软件中试件及模具尺寸与实际试验中常温工况完全一致，模型中材料参数取值见表3．

表3 试件材料参数

选择车辙试验中③号应变片中心对应的模型位置，计算其应变，与试验进行对比．综合图3和图5可以看出：模拟应变结果仍呈现拉压交变的规律，与试验结果一致．二者在数值上有所差异，究其原因，其一是因为模型中水稳层与沥青层之间的层间接触状态假设为完全连续，与真实试验有偏差，可以看出车辆荷载作用对层间接触状态影响较大．其二，应变片测得的应变是平均应变，与模型中数据点选取计算的应变有误差．

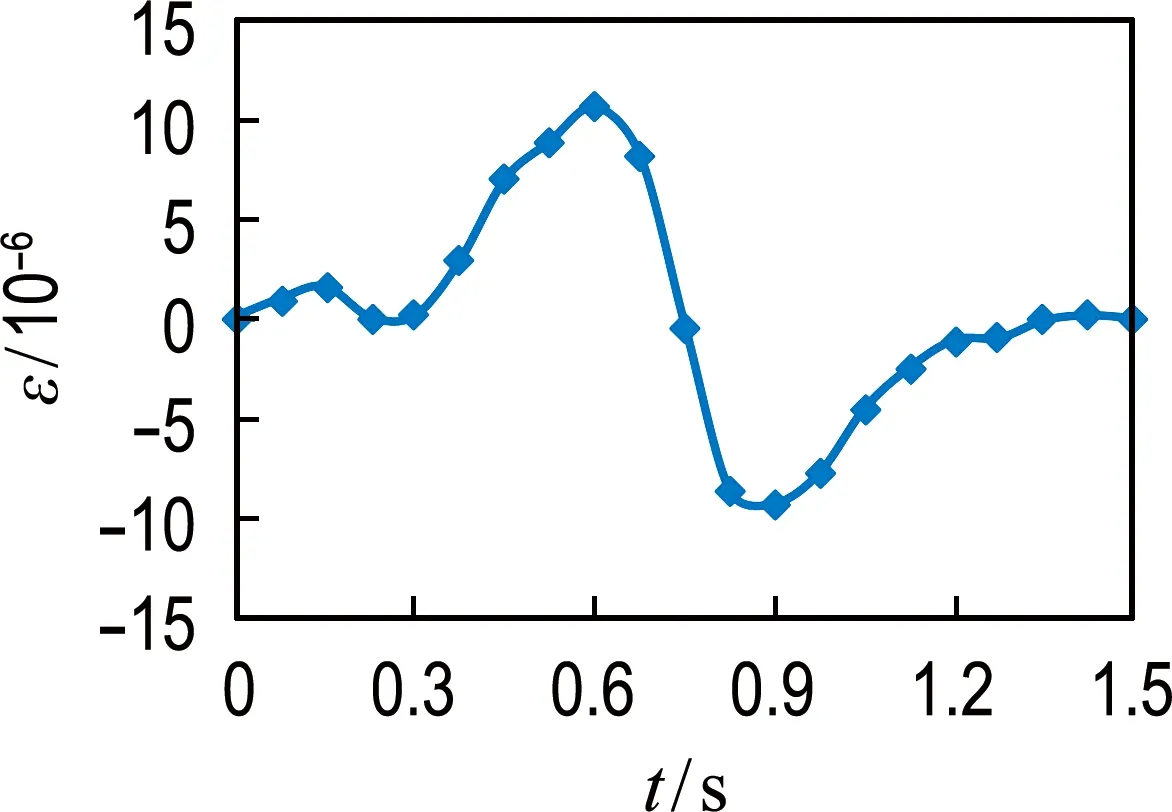
图5 数值模拟沥青层层底应变

3 疲劳性能预估模型的建立

3.1 参数选取

采用沥青层层底拉应变作为疲劳开裂核心，故影响这一参数的因素均会直接影响沥青路面疲劳性能．在此需要说明的是，虽然荷载和轴载组成均会对沥青层层底拉应变造成一定影响，但本文仅针对不同荷载进行研究，不探究轴载组成作用，后期可利用折减系数进行计算．考虑到路基模量变化范围较小，对沥青层层底拉应力的影响不大，本文不作为关键影响因素进行考虑．鉴于此，本文选用沥青层模量(Es)、基层模量(Eb)、基-面层层间摩擦因数(μ)和荷载(P)作为沥青路面疲劳性能预估模型的核心预估变量，则预估模型如下：

Nf=f(N1，N2，N3，N4)=

f(f(Es)，f(Eb)，f(μ)，f(P))

(6)

本文采用荷载为100、120和140 kN，轮胎接地压力对应为0.70、0.707和0.81 MPa[20]，其中100 kN为标准工况．具体参数见表4．

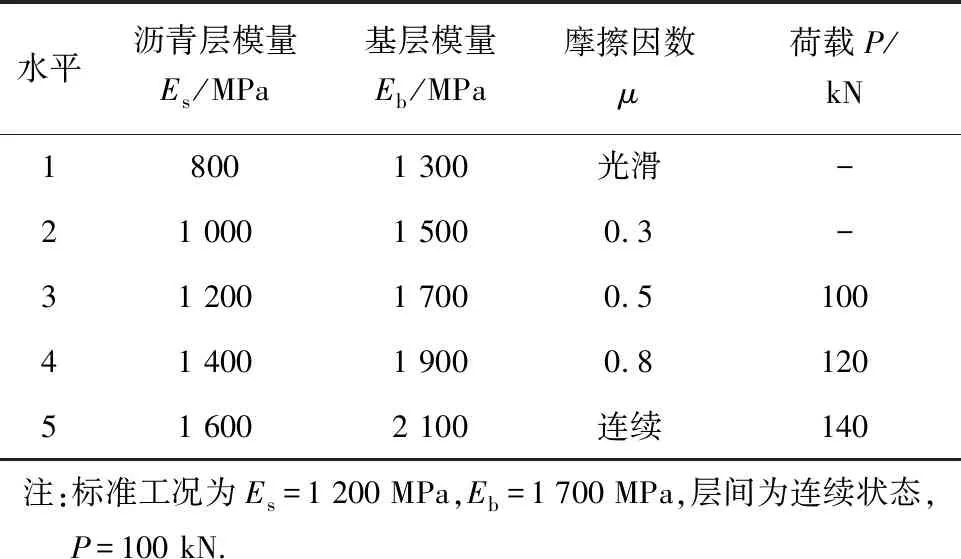
表4 各因素水平表

3.2 疲劳寿命比

设定标准工况并计算沥青路面疲劳寿命，将参数水平不断变换，求出不同工况下路面疲劳寿命，将不同参数条件下疲劳寿命与标准工况疲劳寿命之比记为疲劳寿命比，具体计算如下：

(1)计算标准工况下沥青层层底拉应变，根据式(5)计算得到标准工况下的路面疲劳寿命．

(2)改变某参数水平，此时保持其余参数为标准工况不变，计算该参数不同水平下沥青层层底拉应变，进一步求得各工况路面疲劳寿命．

(3)将该参数在不同水平下疲劳寿命与标准工况下疲劳寿命进行对比，计算此参数不同水平下疲劳寿命比．

(4)将各参数不同水平下疲劳寿命比与该参数进一步回归，得到疲劳性能预估模型中的单项参数．

(5)将各因素的单项参数预估模型进行整合，得到多因素下沥青路面疲劳性能预估方程．

4 典型沥青路面数值模拟分析

4.1 有限元模型的建立

为简便计算，将沥青层简化为一个整体[21]，仅对沥青层整体模量进行取值，探究不同工况下路面疲劳寿命的变化．结构简化前后的形式和简化后模型计算参数见表5、6．

表5 简化前后路面结构形式

模型底面设为ENCASTRE，侧面均无相对位移和其他约束，其他表面无任何约束．选择

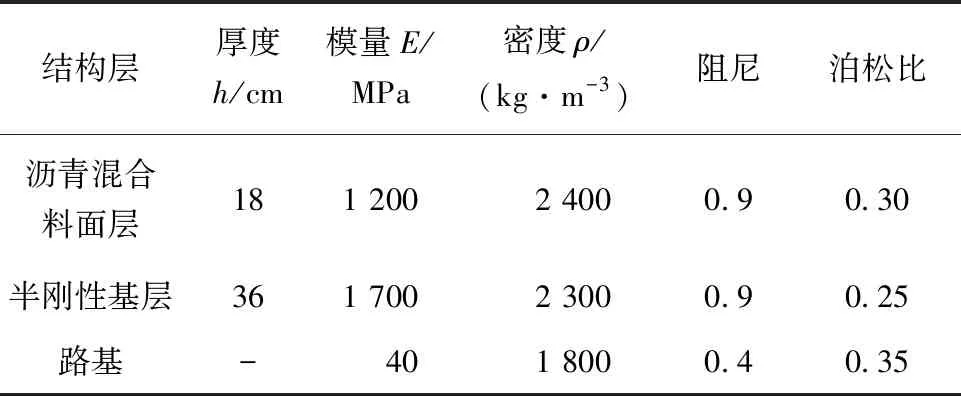
表6 简化后模型计算参数

C3D8R单元．采用非均匀网格划分方法，面层较细，基层略粗，在荷载作用区域进行加密，网格划分见图6．

图6 有限元模型网格划分

4.2 数值模拟结果分析

4.2.1 沥青层模量 根据拟定的标准工况对路面结构进行力学响应分析，保持其余参数不变，改变沥青层模量，由800 MPa逐级增长为1 600 MPa，通过数值模拟分析得到不同工况下沥青层层底拉应变，进一步计算得到沥青路面疲劳寿命．采用标准工况即沥青层模量为1 200 MPa时所得疲劳寿命作为基准，将不同沥青层模量条件下疲劳寿命进行对比，其结果见图7．将不同沥青层模量水平下疲劳寿命比进行回归分析，得到

N1=0.001e0.005 6Es

(7)

4.2.2 基层模量 根据拟定的标准工况即基层模量为1 700 MPa时所得疲劳寿命作为基准，将不同基层模量条件下疲劳寿命进行对比，其结果见图8．将不同基层模量水平下疲劳寿命比进行回归分析，得到

N2=1 367.8e-0.004Eb

(8)

4.2.3 层间接触状态 层间接触状态引起疲劳寿命衰减主要有两方面原因：一是由于层间接触状态的改变不仅引起应力重分布，还会引起应力性质转变，由竖向荷载引起的层底压应力变为拉应力；二是在较大的水平荷载作用下，层间接触状态的改变将会加剧路面疲劳破坏．在交通荷载与水、热、盐等环境因素的耦合作用下，路面结构应力分布对层间接触状态变化更为敏感，对沥青路面结构损伤带来的影响也更为显著，更易出现开裂、车辙和滑移等损坏．

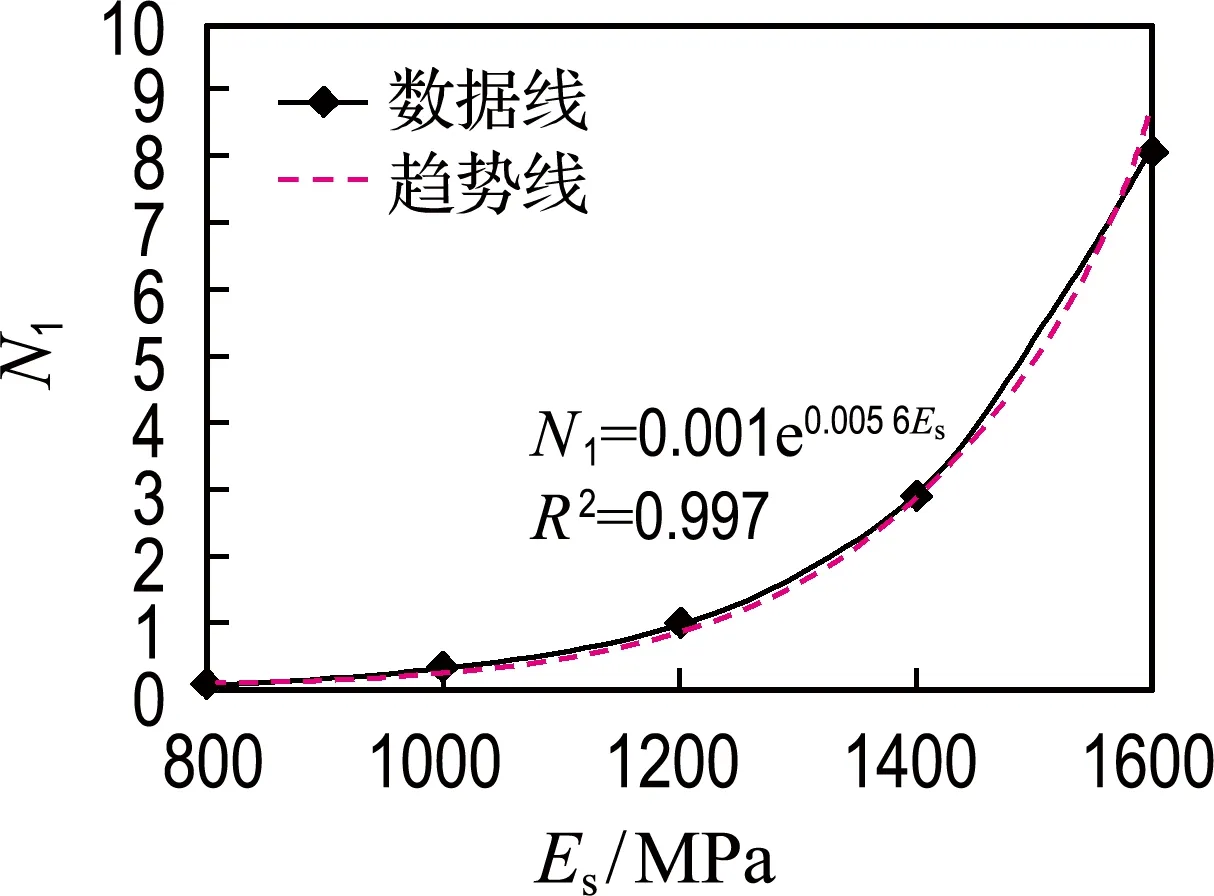
图7 沥青层模量影响

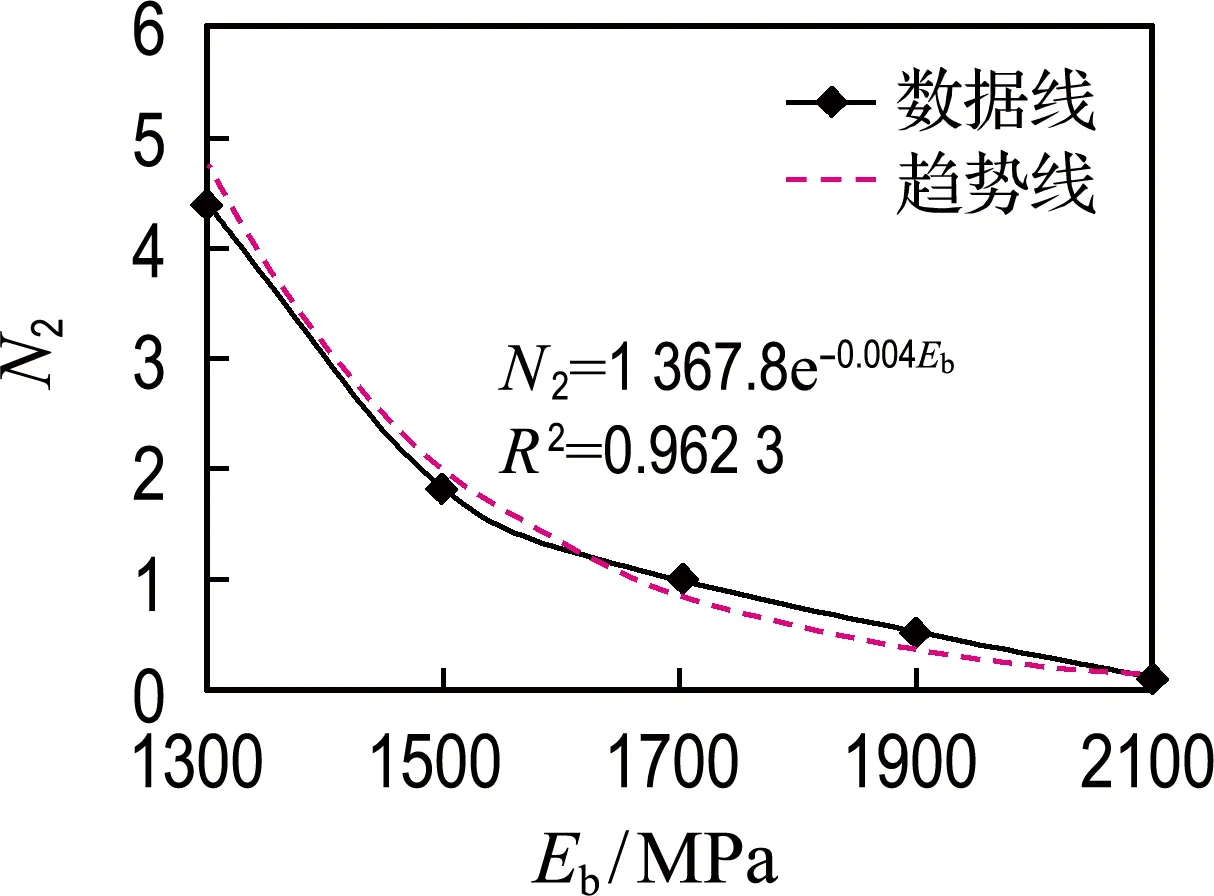
图8 基层模量影响

由于现有路面摊铺水平较高，面层分层铺筑技术成熟，且面层材料模量相差不大，一般认为沥青混凝土上面层与中下面层间为完全连续．对于基层及沥青混凝土面层间接触，本文假设接触面始终处于结合状态，不会产生分离，确保接触面竖向位移和应力传递的连续性[22]，具体设定如下：

(1)假定路面结构各层间均完全连续时，即将路面结构视为一个整体，在模型中将接触属性设为“Tie”．

(2)当基层与面层之间采用摩擦接触，用不同层间摩擦因数分别表征其摩擦特性．

(3)基层与面层之间完全光滑，在模型中将接触属性设为“Frictionless”．

根据拟定的标准工况即层间接触为完全连续(设为“Tie”)时所得疲劳寿命作为基准，将不同层间接触状态下疲劳寿命进行对比，其结果见图9．图9(a)为层间接触状态为连续至光滑全过程对疲劳寿命比的影响，可以看出，由连续至摩擦因数为0.9阶段，层间接触状态的改变量并不大，但由此改变对疲劳寿命比造成的影响十分显著．连续状态是假设的一种理想状态，在实际现场施工和室内试验中无法达到[23]，因此，仅用连续状态作为参考，重点在于研究层间接触为摩擦接触状态．此后，层间接触状态由摩擦因数为0.9逐渐衰减至0.1，由摩擦因数为0.1改变至完全光滑，此阶段中疲劳寿命比的改变在同一张图中显示不出其具体变化．因此，绘制了图9(b)探究层间接触状态由摩擦因数为0.9逐渐衰减至光滑状态对疲劳寿命比的具体影响，将层间接触状态为光滑至 0.9 范围的不同层间接触状态疲劳寿命比进行回归分析，得到

N3=9×10-6μ+6×10-5

(9)

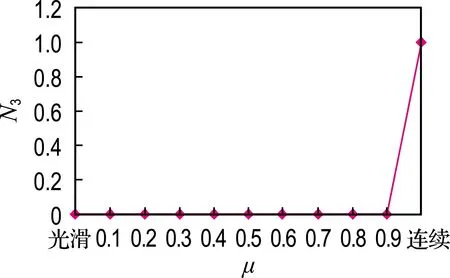
(a) 层间接触状态为光滑至连续

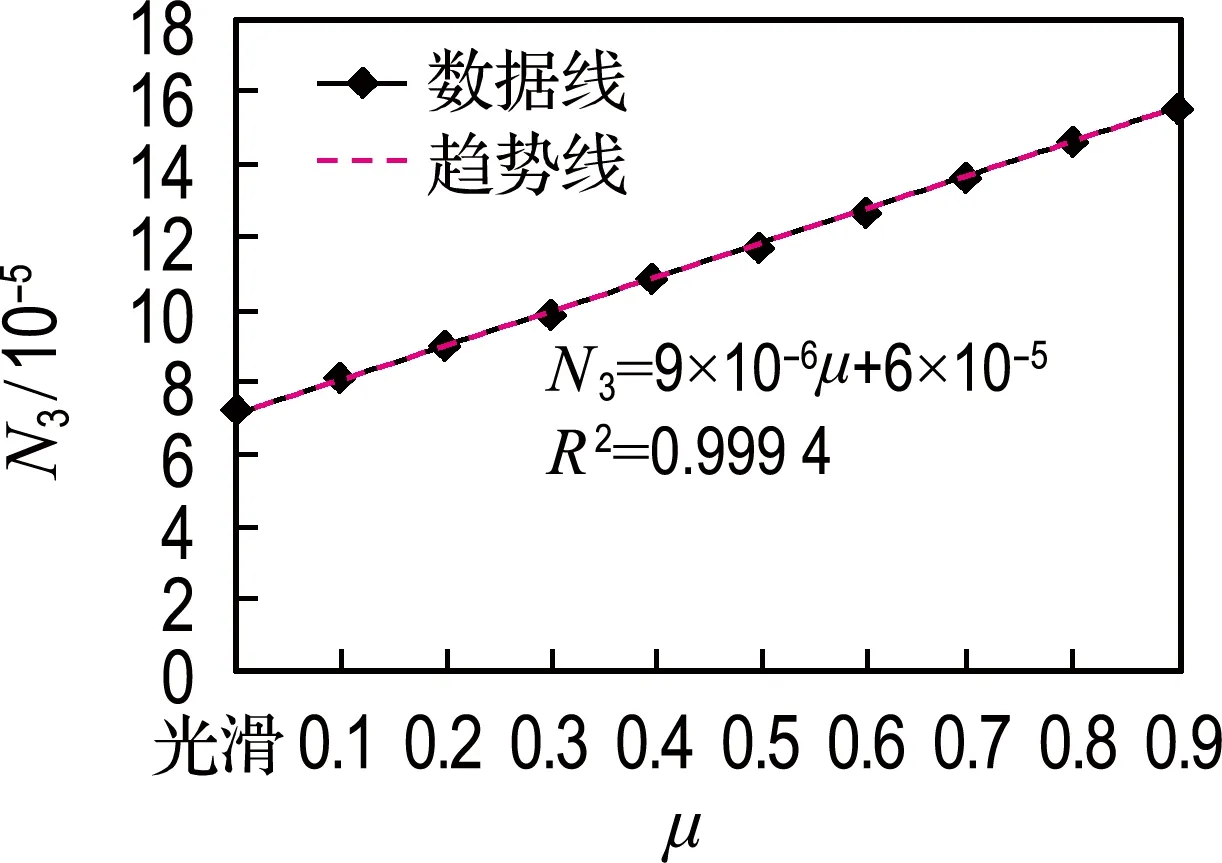
(b) 层间接触状态为光滑至摩擦因数0.9

4.2.4 荷载 同理，采用标准工况即荷载为100 kN 时所得疲劳寿命作为基准，将不同荷载下疲劳寿命进行对比，其结果见图10，回归分析得到

N4=802.55P-1.459

(10)

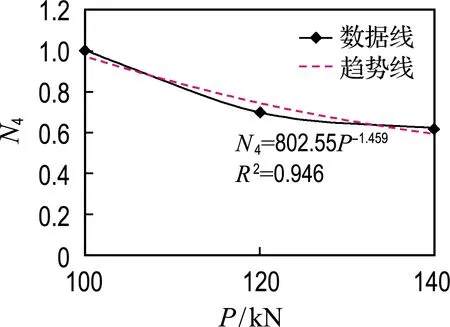
图10 荷载影响

4.3 预估模型建立

根据各单项参数回归结果得到疲劳性能预估模型如下：

Nf=N1×N2×N3×N4

(11)

将各单项参数形式代入式(11)，则疲劳性能预估模型如下：

Nf=0.001e0.005 6Es×1 367.8e-0.004Eb×

(9×10-6μ+6×10-5)×802.55P-1.459

(12)

5 结 论

(1)甄选比对了国内外沥青混合料疲劳破坏模型，参考各参数值，确定了本文疲劳开裂破坏准则．

(2)从车辙试验入手，实测小尺度荷载作用下沥青层层底动态应变，构建等尺度等工况三维有限元模型进行对比验证．

(3)依据开裂准则，得到了沥青层模量、基层模量、层间接触状态及荷载等核心预估变量表达式，建立了考虑层间接触状态的沥青路面疲劳性能预估模型．

(4)层间接触状态对路面疲劳损坏、使用寿命影响显著，首次构建了考虑层间接触状态的沥青路面疲劳性能预估模型，为综合评价沥青路面疲劳寿命，进一步提升路面科学管理提供参考．