四足机器人爬行凸起上坡的运动仿真研究*

王 鹏,董人全,孙铁成,唐 琼

(1.湖州职业技术学院 机电与汽车工程学院,浙江 湖州 313099;2.哈尔滨理工大学 机械动力工程学院,黑龙江 哈尔滨 150080)

0 引 言

四足机器人以四足动物为仿生对象,具有像四足动物那样灵活运动的潜在能力和环境适应力,既有比双足机器人更好的稳定性,又有比六足机器人更简单的机构[1]。斜坡凸起是自然界中常见地形之一,四足机器人在该环境下运动,重心会偏向机身后部,受重力和步态影响,机器人后腿会较前腿受到更大的地面冲击力[2],影响其正常工作,所以研究适用于斜坡凸起环境下的四足爬行机器人腿部结构和步态,对于机器人实现复杂环境下稳定工作具有重要的工程意义和价值。

随着自然学家对四足动物研究的不断深入,例如犬、猫等四足型动物的肌肉-筋腱串联弹性组织,可以在其奔跑运动过程中缓冲地面冲击,增强单腿刚度及柔韧性。美国Kurts.A.[3]研制的四足机器狗首次将气动肌腱技术与关节型机器人结合。日本大阪大学细田实验室[4]采用仿生气动肌腱技术设计了一款仿婴儿爬行机器人。美国波士顿动力公司的BigDog[5]采用液压驱动,并在机器人4个脚踝处配置了减震器,使机器人能够穿越复杂地形。山东大学李贻斌教授[6]研制的仿骡马液压驱动四足机器人,其腿部结构加入了含有直线弹簧的被动缓冲机构。NAKAISHI[7]研制的一款双足步行机器人,使用缠绕钢丝绳的绳轮代替传动驱动关节。LAGODA等[8]则基于扭簧结构,设计了一种紧凑型双重旋转柔性关节,可以通过谐波减速器直接驱动扭簧控制关节柔性输出。

斜坡凸起环境下,四足机器人后腿受到的地面冲击力不仅与其结构中刚柔比例有关,更受机器人爬坡步态的影响。因此,本研究设计电驱式四足机器人柔性腿部结构,并且,针对斜坡地面,对平坦对角小跑步态的抗冲击性和稳定性进行优化,设计斜坡对角小跑步态,接着依据正逆运动学分析获得该步态下机器人转角参数,最后通过四足机器人的步态运动仿真,验证本文设计的合理性。

1 腿部结构设计方案

该腿部结构由4个节段组成,机体和腿部以及腿部节段之间通过旋转关节连接,膝关节采用柔性设计，每个关节均搭配行星减速器,由电机进行驱动。

腿部结构整体设计如图1所示。

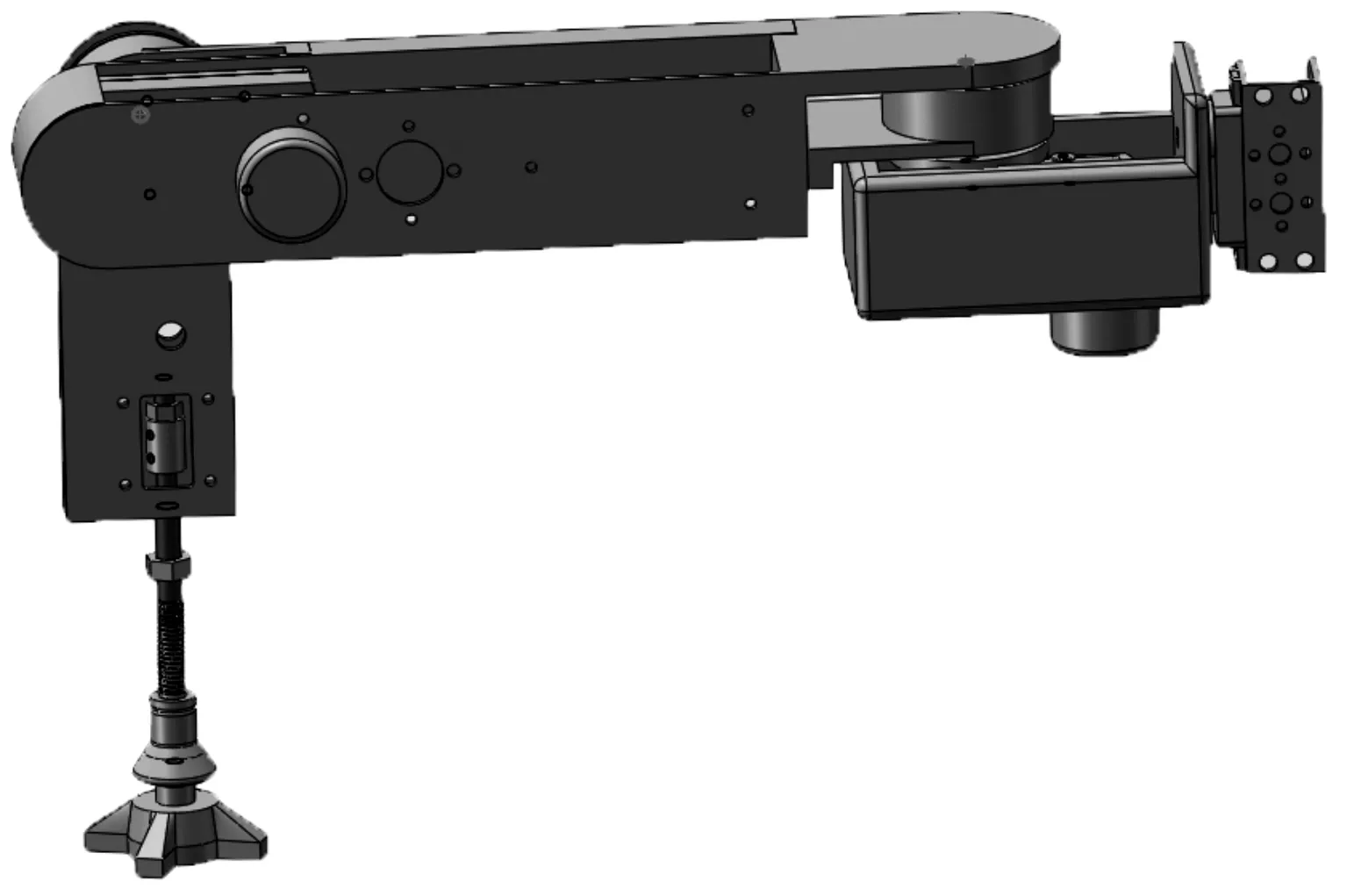
图1 腿部整体结构图

基节、股节的结构设计如图2所示。

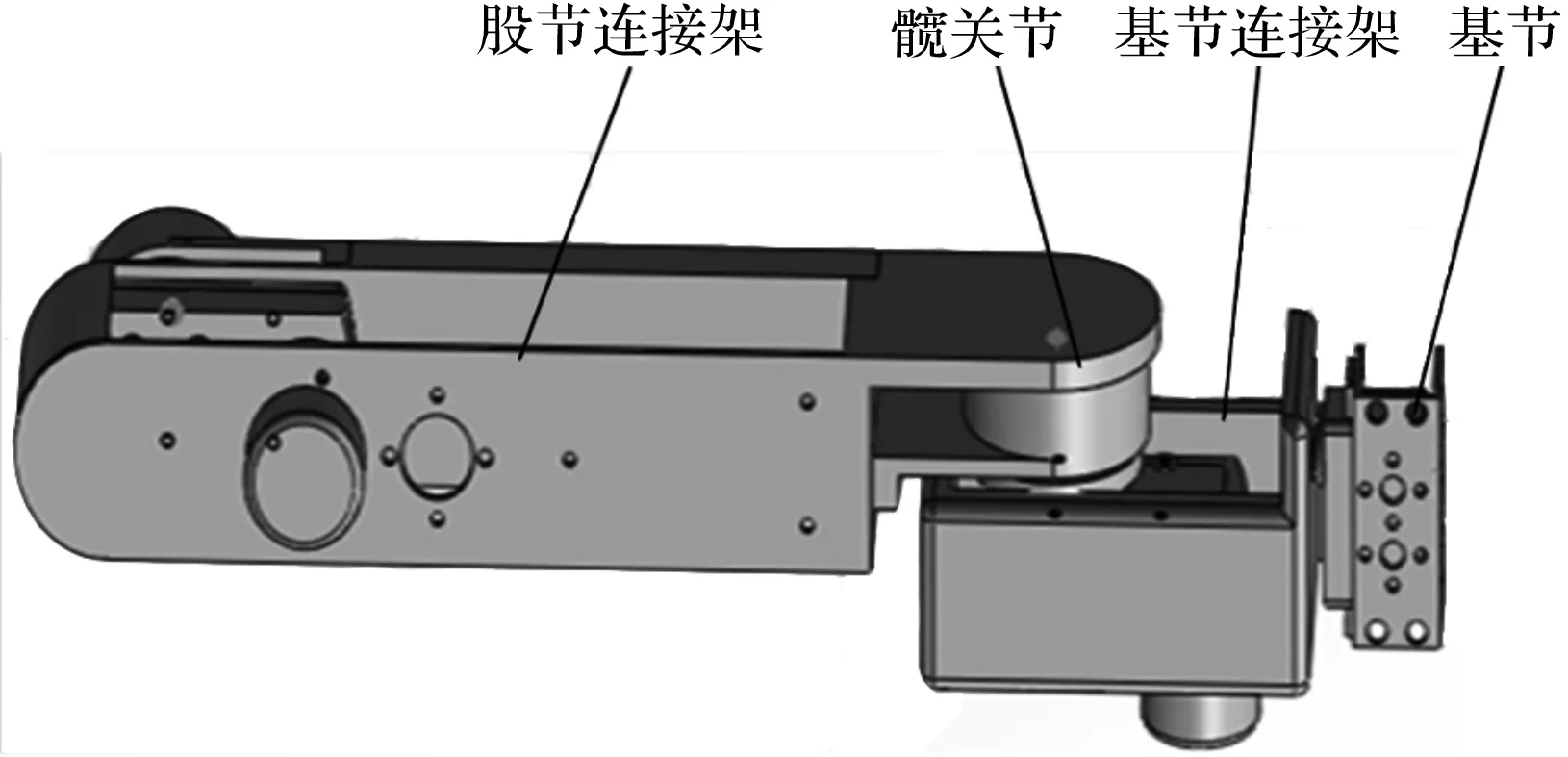
图2 基节、股节的结构连接图

该结构包括基节和髋关节两个自由度,分别对应垂直摆动和纵向摆动;基节的设计可以降低机器人膝关节的横向摆动幅度,减小足端下落时受到的地面反力。基节连接架与股节连接架采用轻质化设计,保证机器人爬行过程中重心的稳定性。

斜坡凸起环境下,四足爬行机器人后腿受到较大地面冲击力时,其膝关节易出现堵转现象,从而导致关节电机损坏和控制精度下降。传统刚性膝关节驱动器可以通过添加压力、位置传感器,配合快速响应的控制、驱动系统,精确控制驱动器输出力矩,模拟实现关节柔顺特性[9]。但是在四足爬行机器人爬行斜坡凸起过程中,能够实现实时控制的驱动机构设计复杂且成本较高,所以笔者在膝关节中引入串联弹性驱动器(SEA),通过在驱动器与被驱动负载间串联弹性元件实现关节柔性输出[10-12],利用弹性元件被动柔性,达到被动适应非结构地形目的,减小地面冲击对膝关节机构的影响。

该柔性膝关节采用弹簧旋转式SEA结构,由安装架、法兰轴、角接触球轴承、弹簧安装架、压缩弹簧输出盘组成,其正视剖面图如图3所示。

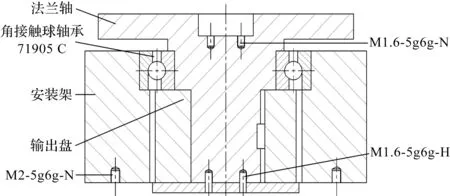
图3 柔性膝关节正视剖面图

依据图3,减速器传来的动力经由法兰轴传递给输出盘,并最后带动胫节运动。

此外,该柔性关节的内部弹簧采用平行放置设计,该关节俯视剖面图如图4所示。

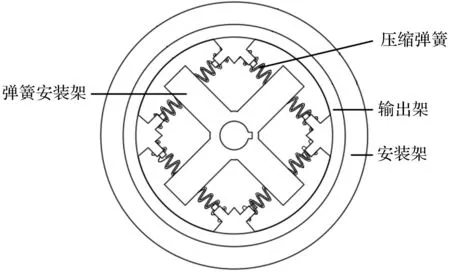
图4 柔性膝关节俯视剖面图

依据图4,弹簧安装架设计为十字板形结构,板形架末端向两侧伸出短齿与弹簧内圈配合;输出盘内壁固定有4个弹簧输出块,输出块向两侧伸出弹簧固定齿;8条处于压缩状态的弹簧对称安装在弹簧安装架与输出盘之间。在斜坡凸起环境下,当四足爬行机器人后腿做抬起迈出动作时,弹簧安装架接受动力发生转动,对称布置的弹簧一侧压缩一侧伸长,通过弹簧恢复力带动输出盘转动;当机器人后腿着地时,受地面反力作用,胫节带动输出架偏转产生逆向扭转力,此时弹簧起到缓冲扭转力的作用,防止堵转现象的发生。

参考犬科四足动物的肌腱减震组织,笔者设计了具有弹簧的胫节机构,如图5所示。

图5 弹性胫节结构图

图5中,当四足爬行机器人橡胶足部接触地面后,脚踝万向节受地面冲击力作用随直行轴承上移,此时弹簧压缩并起到储存能量及缓冲作用,当足部抬起弹簧恢复原位时释放能量。

2 斜坡对角小跑步态规划

对角小跑步态作为四足机器人的常用步态,可以使机器人运动保持稳定性和灵活性[11],但该步态的适用地形为平坦路面。针对斜坡凸起路面,笔者设计一种具有较高稳定性和抗冲击性的斜坡对角小跑步态。该步态时序图如图6所示。

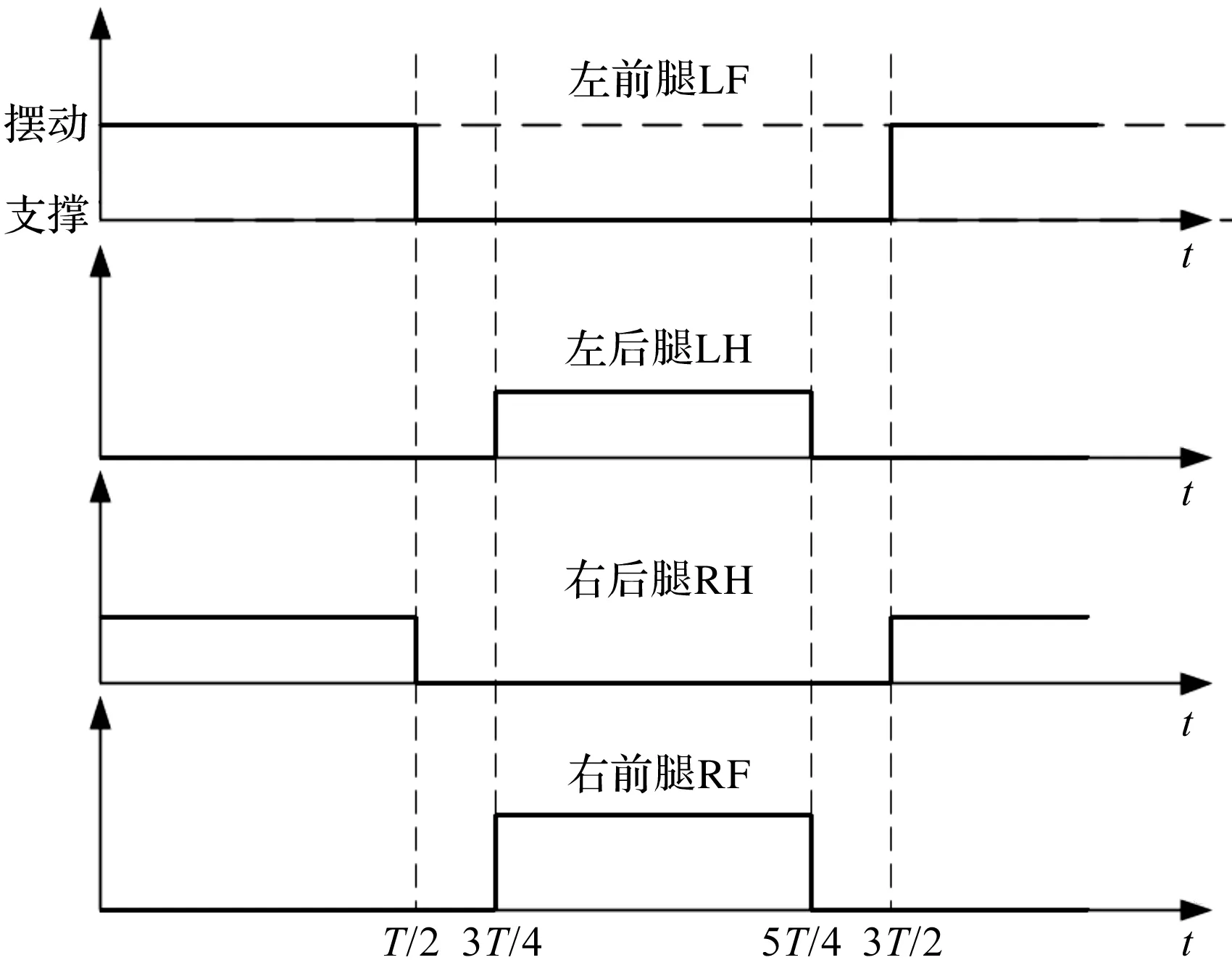
图6 对角小跑步态时序图

图6中,LF、LH、RH、RF分别代表左前腿、左后腿、右后腿和右前腿,步态周期为3T/2,四条腿的支撑与摆动时间均为T/2,对角腿切换运动时存在四足支撑阶段,时间为T/4;此外,四足机器人后腿抬腿高度低于前腿抬腿高度,既降低了重力对机身质心向后偏移的影响,又减小了机器人后腿受到的地面冲击力。

在斜坡凸起环境下,对角小跑步态图如图7所示。

图7 斜坡对角小跑步态图

从图7(a)可以看出,四足爬行机器人处于初始状态,之后迈出左前腿与右后腿,如图7(b)所示;当两腿摆到最大位置后,摆动相转为支撑相,此时机器人四条腿均为支撑状态,如图7(c)所示;待机器人短暂的四足支撑后迈出右前腿和右后腿,如图7(d)所示;当两腿摆到最大位置后转为支撑相,此时机器人再次进入四足支撑状态,如图7(e)所示;待机身稳定后,左前腿与右后腿回到初始位置,如图7(f)所示;至此四足爬行机器人完成斜坡对角小跑步态的一个运动周期。

为了适应斜坡凸起环境,防止机器人失衡,与平坦环境下对角小跑步态相比,机器人在对角腿运动后,加入四足支撑阶段,为四足机器人的爬坡运动提供了缓冲地面反力和稳定重心的时间。

3 四足爬行机器人单腿运动学分析

为了得到步态规划后腿部各关节转角参数,笔者进行了正、逆运动学分析。首先建立了斜坡凸起环境下四足爬行机器人的运动学模型。

该四足爬行机器人每条腿有3个自由度分别位于基节、髋关节、膝关节,根据D-H法建立四足爬行机器人的关节连杆坐标系,以单腿为例,如图8所示。

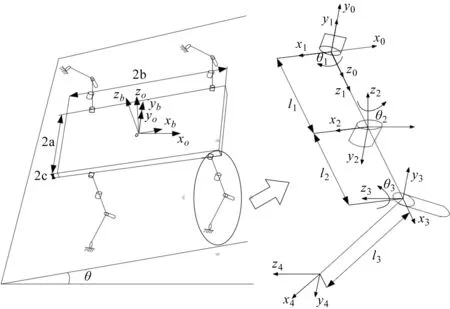
图8 右前腿部D-H建立简图oxoyozo—机器人的伴随坐标系;oxbybzb—机体坐标系;ox1y1z1,ox2y2z2,ox3y3z3,ox4y4z4—基节、髋关节、膝关节、足端的坐标系;θ1,θ2,θ3—基节、髋关节、膝关节的旋转角度;l1,l2,l3—基节到髋关节之间的杆长、髋关节到膝关节之间的杆长、膝关节到足端之间的杆长;2b,2a,2c—机身的长、宽、高;θ—斜坡倾角

四足爬行机器人单腿杆件及关节参数如表1所示。

表1 四足爬行机器人单腿杆件及关节参数

由表1可知腿部各连杆长度、扭转角和夹角等参数信息,i坐标系和i-1坐标系的齐次变换矩阵为:

(1)

由式(1)和表1参数可得如下矩阵:

(2)

(3)

(4)

(5)

(6)

(7)

式中:ci—旋转齐次变换矩阵的元素cosθi;si—旋转齐次变换矩阵的元素sinθi;i—坐标系序号,θ—斜坡的倾斜角度。

由式(2～7),可得到足端相对于机体坐标系的转换矩阵bT4:

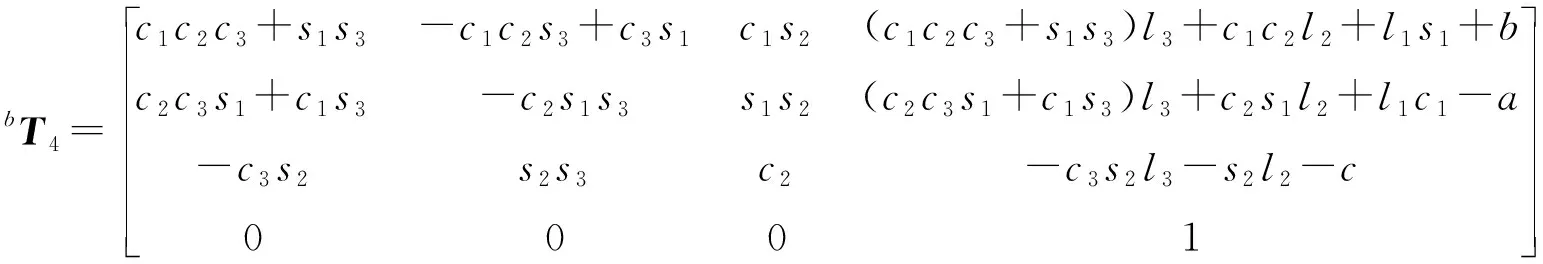
(8)

由式(6,7)可得足端相对于伴随坐标系的矩阵:

(9)

解得四足爬行机器人足端位置为:

(10)

其中：

t1=(c1c2c3+s1s3)l3+c1c2l2+l1s1+b

(11)

t2=-c3s2l3-s2l2-c

(12)

通过式(2～10)得到了四足爬行机器人足在伴随坐标系下的位置和姿态,由上文的步态规划可知足端的运动轨迹,为了获得对角小跑步态下腿部各关节的转角参数,此处运用逆运动学对这条腿3个关节的转角进行反向求解:

(13)

通过式(13)可以反解出3个关节(基节、髋关节、膝关节)的转角,依据步态规划中足端的运动轨迹,可获得基节、髋关节和膝关节的最优转角参数,如表2所示。

表2 斜坡对角小跑步态关节的最优转角参数

由表2可知,斜坡对角小跑步态下,四足爬行机器人后腿膝关节转角较前腿小,这为后续机器人步态仿真提供了数据。

4 四足机器人爬行凸起上坡运动仿真

依据步态规划和表2斜坡对角小跑步态的关节转角参数,笔者在Adams平台中设定四足机器人的爬坡驱动函数,斜坡对角小跑步态周期设为3 s,摆动相和支撑相均设为1 s,四足爬行机器人仿真场景如图9所示(由右手定则可得Y轴为垂直斜坡的竖直方向,X轴为纵向,Z轴为横向)。

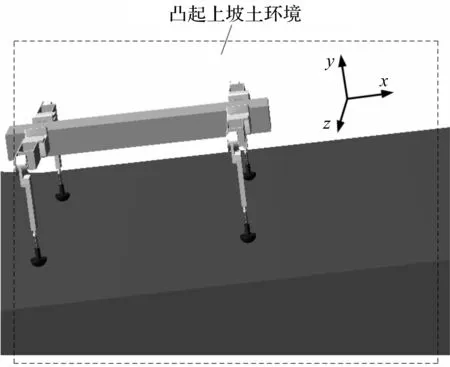
图9 四足爬行机器人仿真场景

在斜坡凸起环境下,四足机器人质心在三维坐标系中的变化可以反映机器人的运动轨迹和运动姿态,从而表达四足爬行机器人运动的稳定性。本文主要是从Y轴方向对比斜坡、平坦对角小跑步态的质心位移曲线,揭示斜坡对角小跑步态的高稳定性。

质心位移曲线如图10所示。

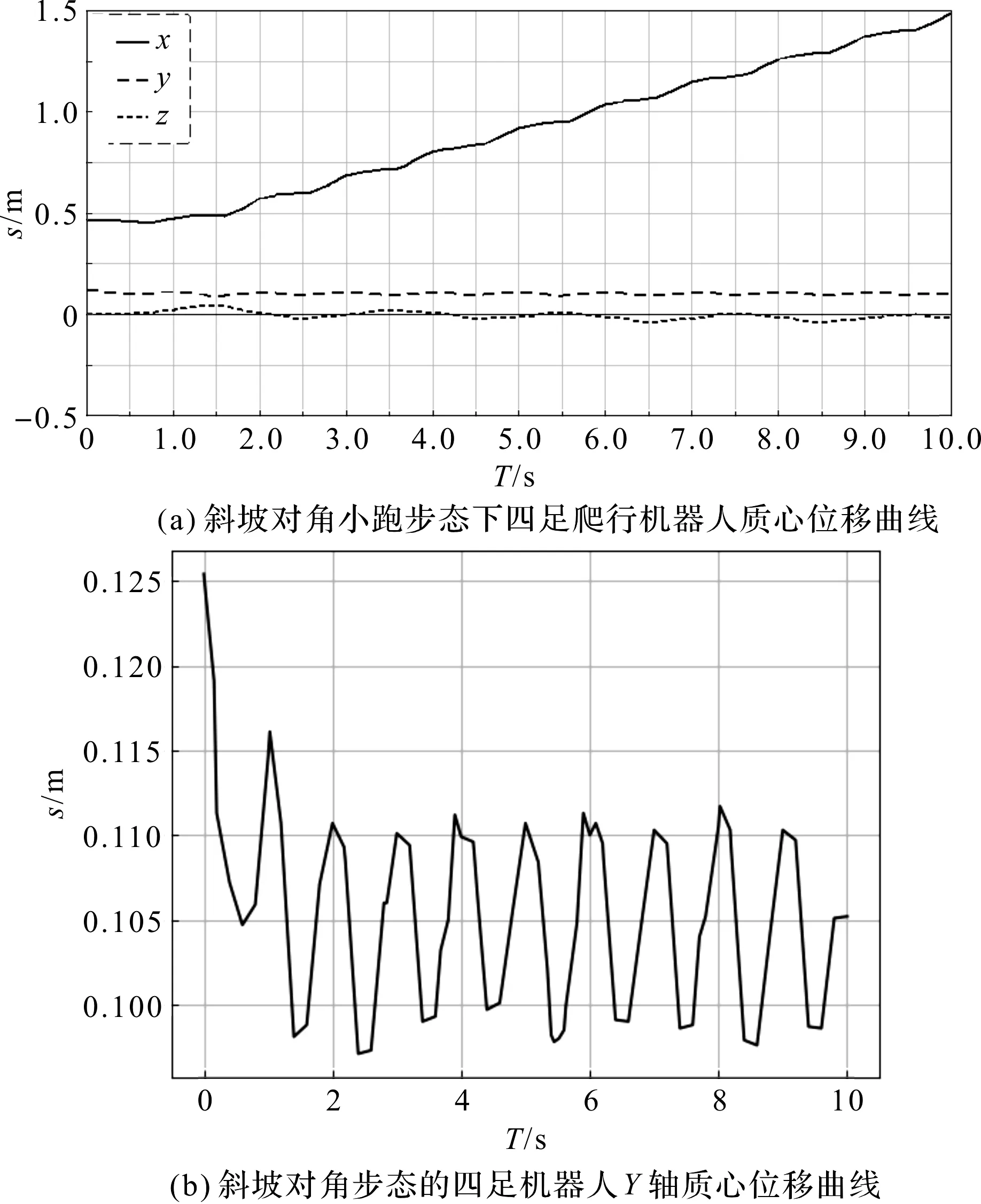
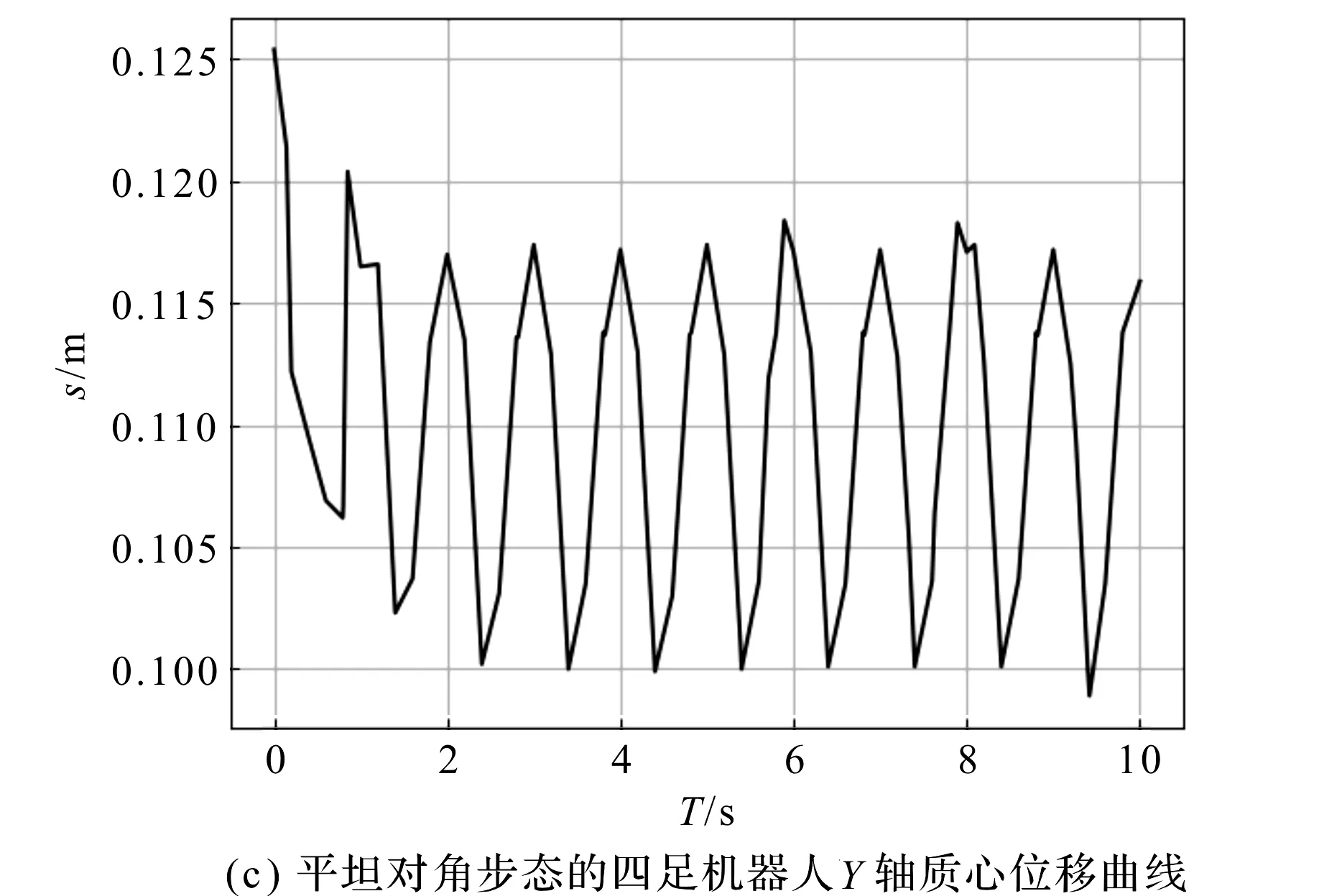
图10 对角小跑步态下四足爬行机器人质心位移曲线

仿真结束后,笔者将Adams仿真数据导出,并转换为.scv格式,再使用Python3.6对仿真数据进行特定情形分析;结合图10,从X、Y、Z轴3个质心移动方向进行机器人运动情况分析:

(1)X轴曲线代表了四足爬行机器人爬越过程中的前进方向,由图10(a)中可知,曲线斜率基本稳定在固定值,说明机器人在X轴方向匀速前进;

(2)Y轴曲线反映了四足爬行机器人的在运动过程中的颠簸程度,由图10(b～c)可知,两种对角小跑步态下四足爬行机器人的Y轴质心位移曲线存在波动且最大处均在2.2 s左右,产生波动的原因是对角小跑步态中存在两腿支撑状态,机身因重力原因发生竖直方向的微小倾斜,采用平坦四足小跑步态的四足爬行机器人曲线波动数值约为0.017 5 m,采用斜坡四足小跑的步态四足爬行机器人的曲线波动数值约为0.015 m,证明本研究设计的腿部结构在搭配斜坡对角小跑步态后,机器人机身在Y轴的倾斜角度更小,爬行重心更加稳定;

(3)Z轴是四足机器人在运动过程横向偏移程度,由图10(a)可以看出,曲线在0附近偶有波动,是因为对角小跑步态存在两腿支撑阶段,机身因重力发生倾斜而产生微小偏移,支撑相不同时产生的正负偏移互相抵消,机器人依然按照轨迹爬行。

采用斜坡对角小跑步态、平坦对角小跑步态的四足机器人足端接触力曲线如图11所示。

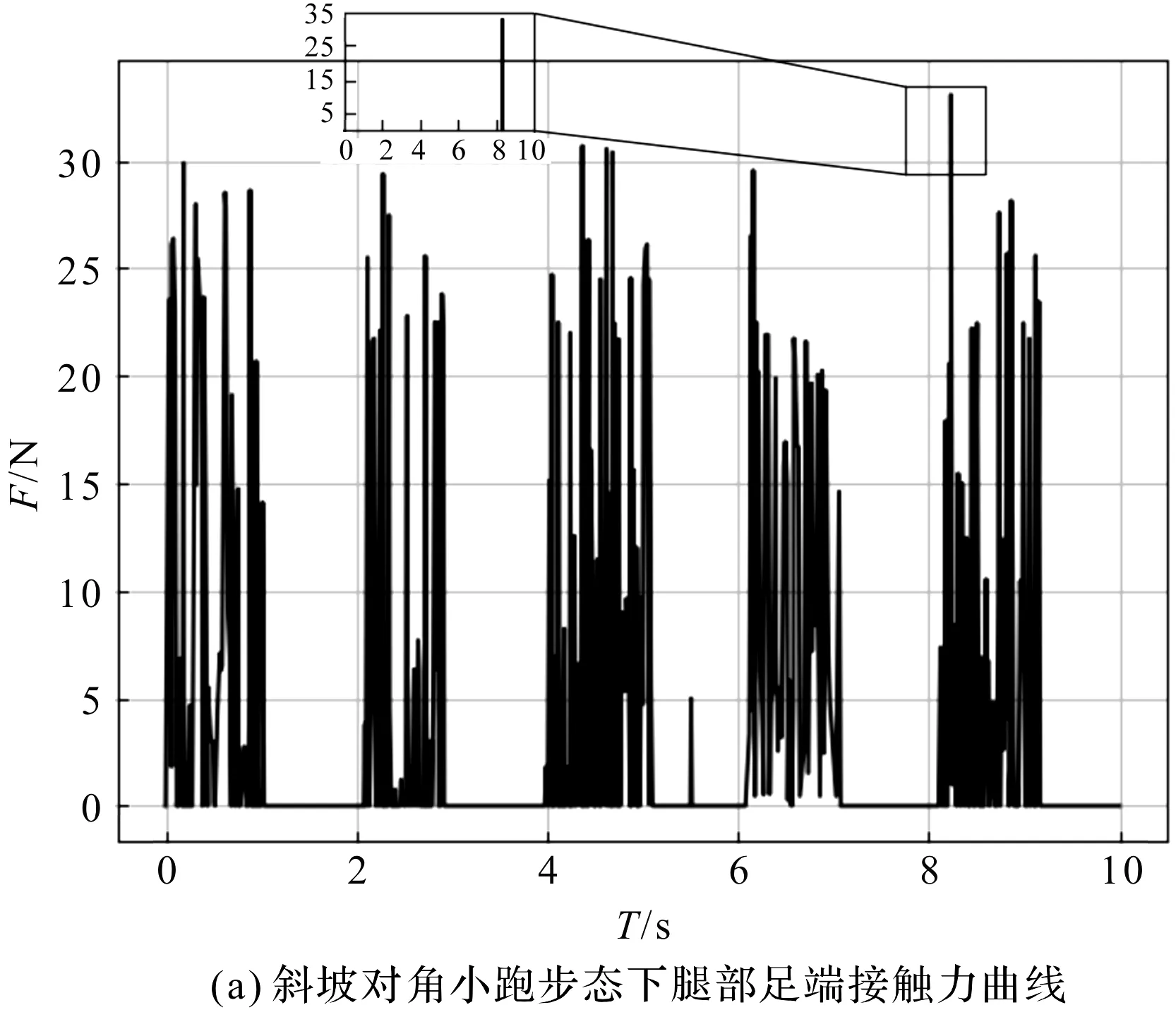
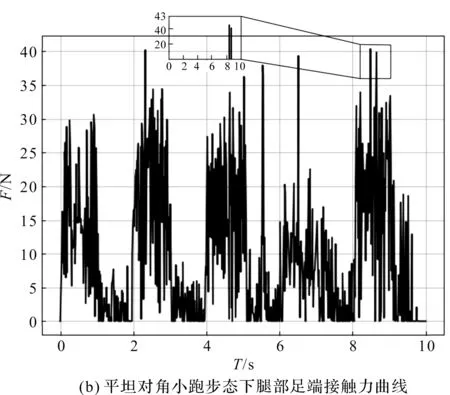
图11 两种对角小跑步态下腿部足端接触力曲线

由图11(a～b)可知,斜坡对角小跑步态下的四足爬行机器人足端所受接触力最大峰值约为33 N,平坦对角小跑步态下的四足爬行机器人足端所受接触力最大峰值约为41 N,斜坡对角小跑步态下腿部足端接触力比平坦四足小跑步态下足端减小了8.05%,且前者存在四足支撑阶段,避免腿部连续受地面冲击力,为腿部结构提供了缓冲地面冲击力的时间,证明在斜坡凸起环境中,斜坡对角小跑步态可以提高四足机器人腿部的抗冲击性。

5 结束语

本文主要设计了一种四足机器人爬行步态,在设计柔性腿部结构后,对平坦路面的对角小跑步态进行优化,规划了一种适用于斜坡凸起环境的对角小跑步态;随后通过正、逆运动学仿真获得步了态转角参数,从而完成了机器人步态运动仿真;

在仿真分析过程中,通过比较平坦、斜坡两种对角小跑步态的四足爬行机器人质心位移曲线和足端接触力曲线,证明了本文设计的斜坡对角小跑步态可以使四足机器人的质心更加平稳,且机器人腿部足端接触力小于平坦对角小跑步态下腿部足端接触力,前者最大峰值比后者小8.05%。

在后续的设计改进中,将深入研究搭配有该腿部结构的四足机器人爬越斜坡凸起时稳定步态切换的控制方法,进一步改善四足爬行机器人运动过程中的足端受力和运动稳定性。