改进模糊PID方法及其在电液伺服控制中的应用*

陈 帅,汪成文,2,3*,张震阳,吉鑫浩,赵赞魁

(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.太原理工大学 新型传感器与智能控制教育部/山西省重点实验室,山西 太原 030024;3.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310058)

0 引 言

因具有功重比大,能够以高精度和快速响应来驱动大惯量和重负载的特点,电液伺服系统在各行各业都得到了广泛的应用,尤其是在工业现场和国防武器系统中应用最为普遍,如挖掘机上大臂小臂的驱动系统、涡轮机的变桨系统、舰船火炮的驱动系统等[1-3]。

学术界和工业界对高性能电液伺服控制技术的需求越来越来迫切。然而,在实际工作中,随工况的变化,电液伺服系统的泄漏系数、阻尼、刚度等参数都是时变的,而且系统所受的外界干扰也是不确定的,因此,由一组预先设定好的控制参数值往往不能满足工况需求,并确保系统具有良好的控制效果。对此,研究人员引入了拥有智能化特点的模糊控制与PID控制相结合的复合控制算法—模糊PID控制算法。模糊PID控制算法可解决PID控制参数固定不变的问题,又可以使控制算法在系统数学模型未能精准创建的情况下,兼具优异的伺服控制性能和鲁棒性[4,5]。

国内外部分高校和研究单位对模糊PID进行了相关研究与应用:李文静等人[6]345将模糊PID控制器应用于列车制动电液控制系统中,对高频电磁阀的开关动作进行了调控,实现了制动系统压力的比例控制。葛雷等人[7]11将模糊PID控制器运用在工业蝶阀电液伺服控制系统中,验证了模糊PID的控制效果明显优于PID控制。LIU F C等人[8]356利用模糊PID控制器对空间操纵器进行了控制,并与PID控制进行了对比,发现模糊PID的控制性能对机械臂的轨迹控制更为有效。钟定清等人[9]663在模糊PID控制器的基础上引入了支持向量回归预测算法,提出了一种支持向量机模糊PID控制策略,实现了交流电力测功机控制系统的“超前”控制。LUO Q Z等人[10]3362提出了一种前馈模糊逻辑PID算法,在抗干扰性能和跟踪精度方面都得到了有效的提升。BOUKHALFA G等人[11]1887将粒子群优化算法与模糊PID算法相结合,利用粒子群算法对模糊PID的比例因子进行了优化,并将该控制策略应用于双星感应电机直接扭矩控制中,结果表明该控制策略有效减少了高转矩脉动,以及缩短了上升时间。其中,文献[9-11]所提的与其他先进算法结合的复合模糊PID控制策略,虽然在一定程度上进一步提高了系统的性能,但其算法结构复杂、计算成本大。此外,文献[6-8]以及文献[12-17]均是对传统模糊PID控制算法的研究与应用。

对上述文献中模糊PID控制算法的模糊规则库进行分析,可以得出其对PID 3个参数Kp、Ki、Kd进行在线调整的修正机制是PID整定的专家经验[18，19]。

目前,大多数关于模糊PID的研究都是基于传统的模糊规则库开展的,传统模糊规则库存在的问题是:传统模糊PID控制算法依据ΔKp规则库对PID的Kp参数进行在线修正时,ΔKp规则库中的部分规则与PID整定的专家经验存在矛盾,致使对Kp参数进行在线修正时精准度不足。例如,当误差|e|较大时,为使系统能尽快达到稳态,且能以较高的精度跟踪指令信号,依据PID整定经验,无论误差的变化趋势如何,此时的Kp值应取大值,但传统模糊PID的ΔKp规则库中的部分规则反而会使Kp值减小。如当E、EC均为正大PB时,此时依据PID整定经验,Kp值应取大值,然而,传统模糊PID规则库中ΔKp对应的是负大NB,反而使Kp值变小,产生矛盾。

针对上述问题,笔者提出一种改进模糊PID算法。

1 控制对象系统描述

笔者以典型的电液位置伺服阀控缸系统为控制对象,其结构如图1所示。

图1 电液位置伺服阀控缸系统示意图xd—给定信号;xp—作动器活塞杆的位移,控制器做差值控制调节伺服阀的开口大小,实现位置闭环控制

2 模糊PID控制器设计

2.1 模糊PID控制器结构

模糊PID控制器采用双输入三输出的形式,以液压缸活塞杆输出位移的误差e(t)和误差变化率ec(t)为输入,输出为PID 3个参数的增量ΔKp、ΔKi、ΔKd。

PID控制参数在线修正公式如下:

(1)

式中:Kp0,Ki0,Kd0—PID控制器的初值;Ke,Kec—量化因子;KΔp,KΔi,KΔd—比例因子。

模糊PID控制器结构如图2所示。

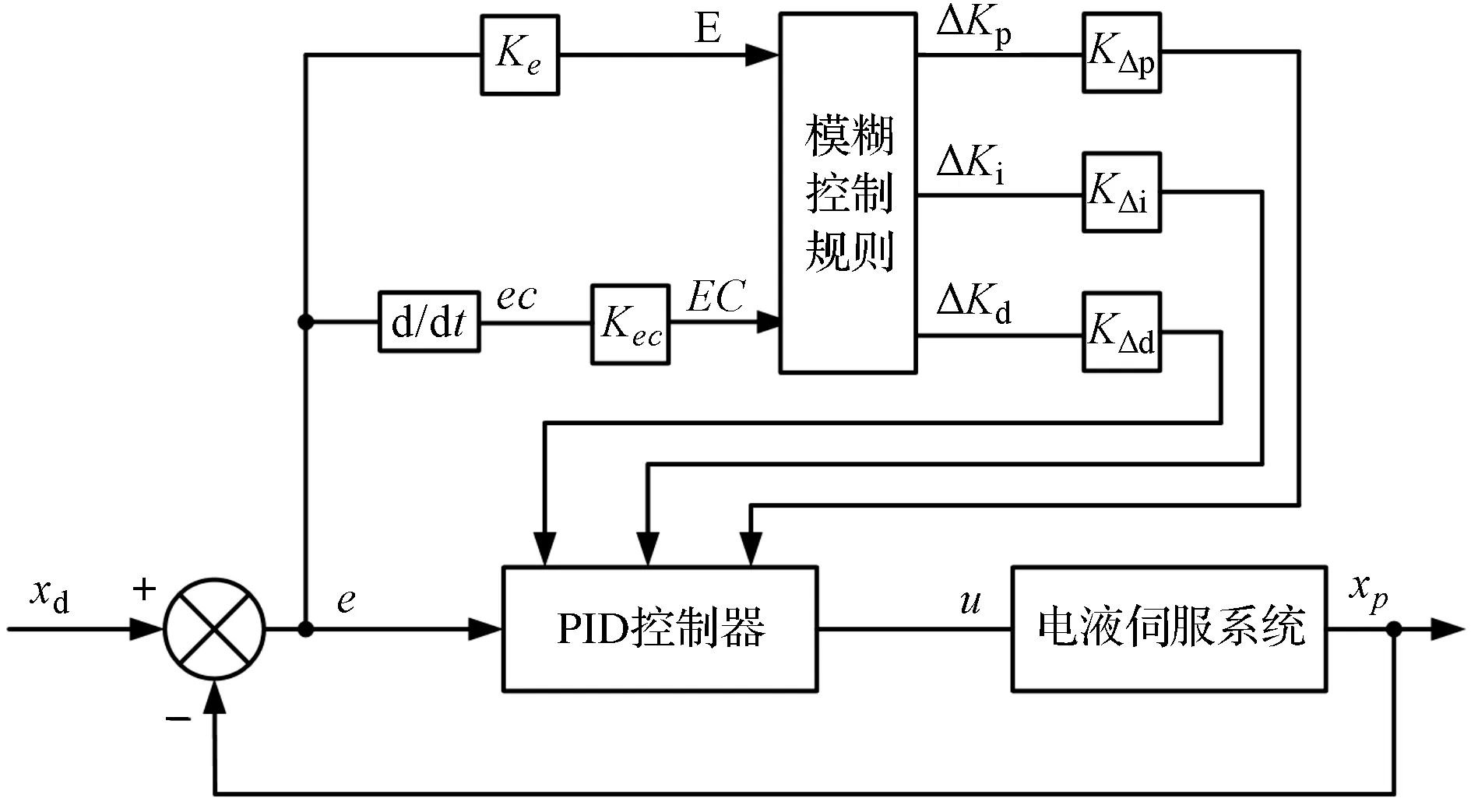
图2 模糊PID控制器结构示意图

2.2 规则改进模糊PID(FPID)控制策略

隶属函数的选取直接影响着系统的控制性能。一般在误差比较大的场合,选取分辨率低的隶属函数smf或zmf,在误差接近于0的情况下,笔者选取分辨率高的隶属函数trimf,故选取传统模糊PID算法和规则改进模糊PID算法的输入/输出变量中7个语言变量:NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)所对应的隶属函数均分别为zmf、trimf、trimf、trimf、trimf、trimf、smf,其分布如图3所示。

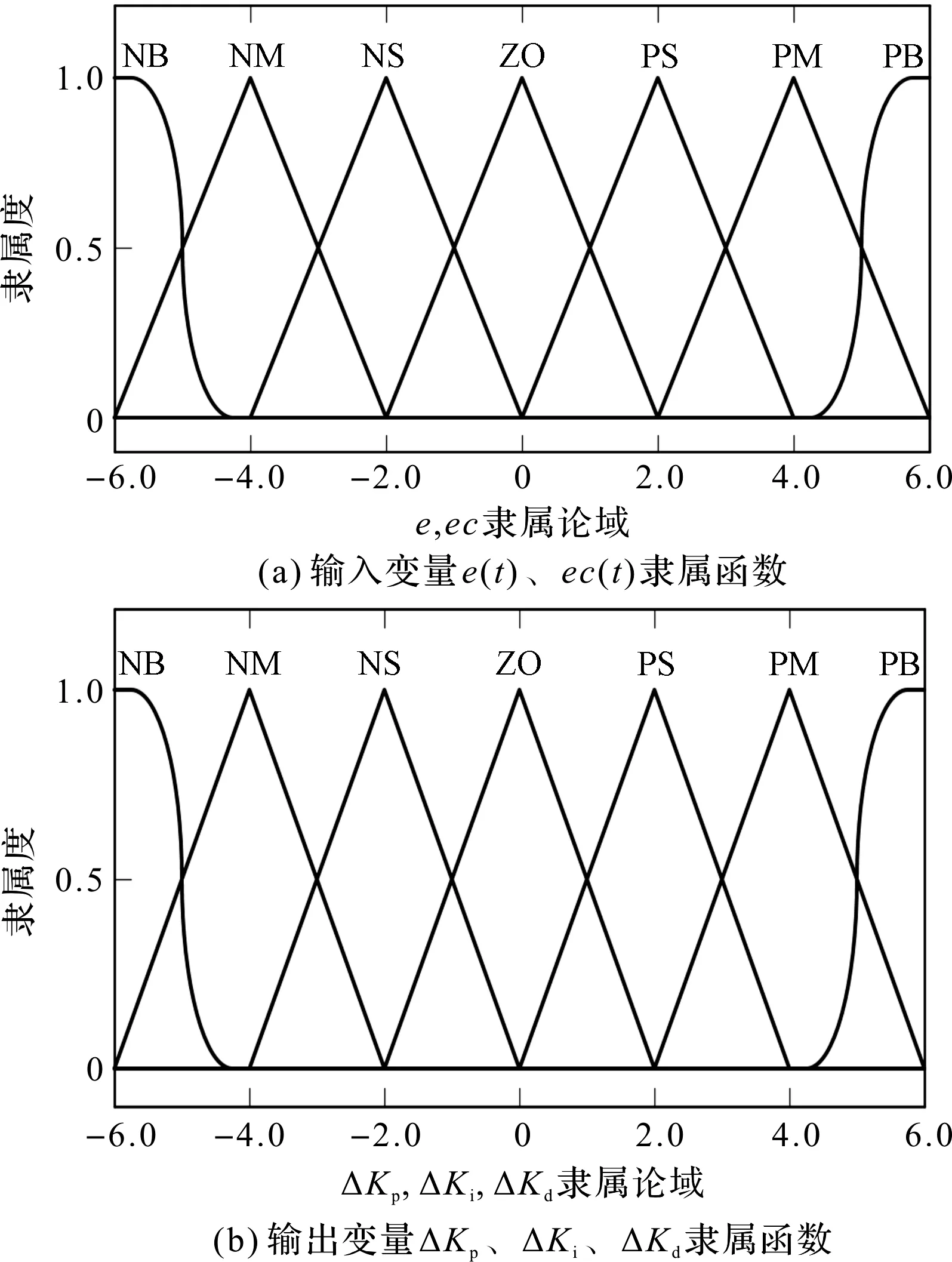
图3 输入/输出变量隶属函数分布图

根据PID整定的专家经验,并参考论文对传统模糊PID控制器中模糊控制规则库的编制规律,针对传统模糊PID中模糊规则库存在的问题,笔者对传统模糊PID的ΔKp规则库进行分析,明确哪些规则与PID整定的经验不符,对其进行修正与改进,并通过仿真实验做进一步的调整,即可形成新的ΔKp规则库。

传统的模糊PID的规则库如表1所示。

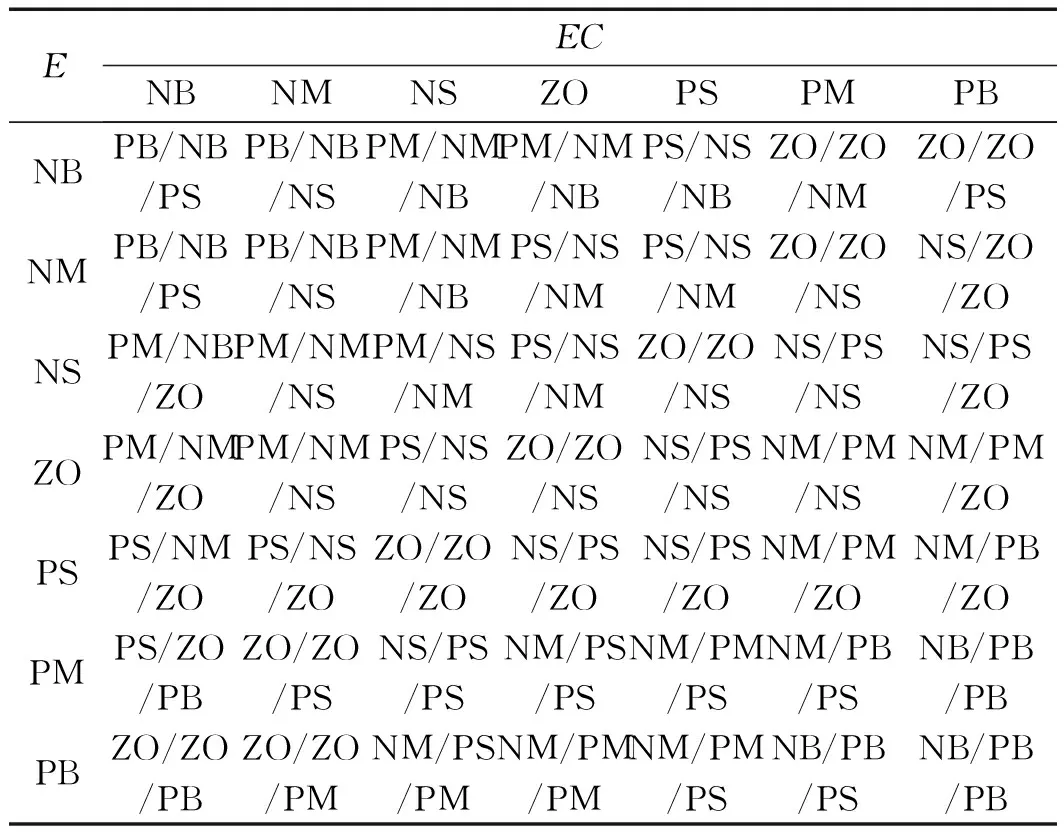
表1 传统的ΔKp、ΔKi、ΔKd模糊规则库

新的规则改进后的模糊PID的模糊规则库如表2所示。

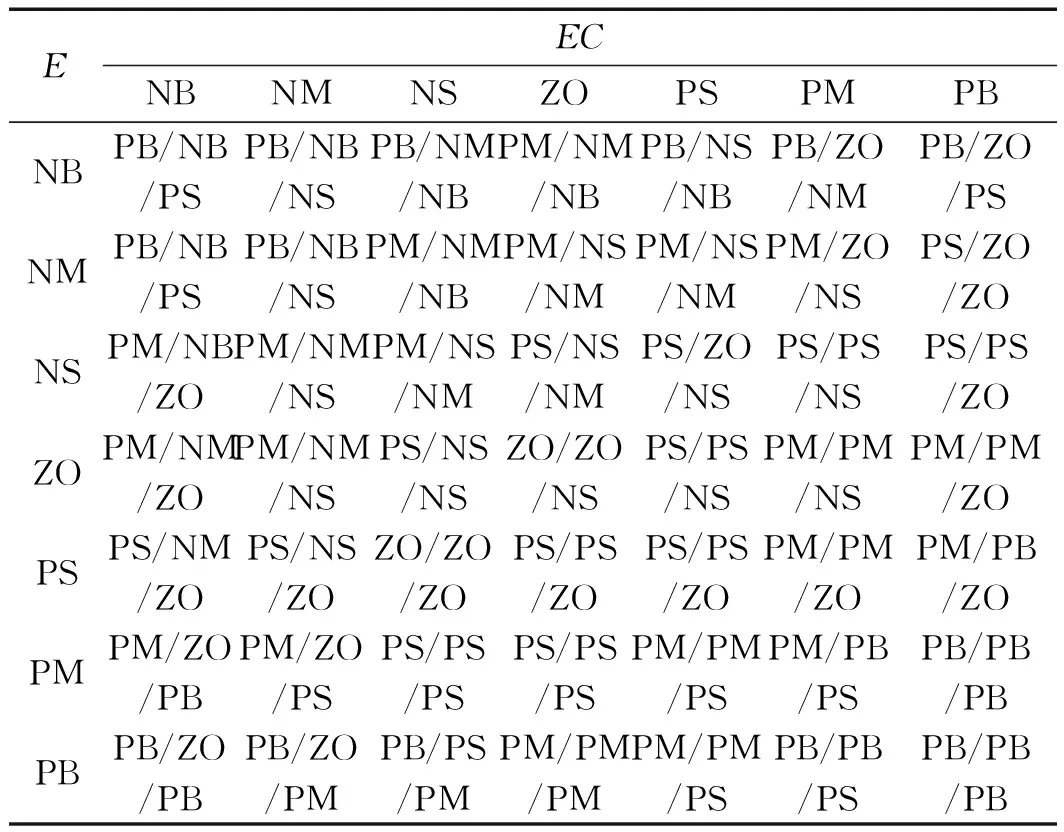
表2 规则改进后的ΔKp、ΔKi、ΔKd模糊规则库

ΔKp规则库改进思路:

若e(t)·ec(t)>0时,表明系统的输出随时间的推移趋于发散状态,即误差|e(t)|会越来越大,此时为了快速降低误差使系统能再次达到稳态,就必须适当增大Kp。由公式Kp=Kp0+KΔp·ΔKp(KΔp>0)可知,此时,模糊控制应输出一个正的ΔKp值;因此,当误差|e|较大时,为使系统具有快速的响应能力,ΔKp应取大值,故当E、EC均为PB时,ΔKp应为PB,而传统模糊PID的ΔKp规则库中对应的为NB(模糊控制输出的ΔKp值为负),产生矛盾,因此需对此条规则进行调整;当误差|e|减小为中等大小时,为保证系统即具有足够的响应能力,又能避免产生较大的超调,ΔKp应取适中值,故当E、EC均为PM时,ΔKp应为PM,而传统模糊PID的ΔKp规则库中对应的为NM(模糊控制输出的ΔKp值为负),产生矛盾,因此需对此条规则进行调整;当误差|e|较小时,为避免系统在达到稳态时出现振荡,ΔKp应取小值,故当E、EC均为PS时,ΔKp应为PS,而传统模糊PID的ΔKp规则库中对应的为NS(模糊控制输出的ΔKp值为负),产生矛盾,因此需对此条规则进行调整;根据该思路便可完成对ΔKp规则库中E与EC同号规则的优化与改进。

同理,若e(t)·ec(t)<0时,表明系统的输出随时间的推移趋于收敛状态,即误差|e(t)|会越来越小,此时为了使系统的输出稳定在稳态值附近,只需根据偏差|e|的大小和偏差变化率|ec|的快慢对ΔKp适当取值即可;根据该思路便可完成对ΔKp规则库中E与EC异号规则的优化与改进。

新的规则改进后的模糊PID控制器的ΔKp规则库,与传统的模糊PID控制器的ΔKp规则库的差异,可通过ΔKp规则库的曲面图直观地反映出来,如图4所示。

图4 不同规则库下的ΔKp规则库曲面图对比

3 仿真验证

笔者以阀控对称缸系统为被控对象,对规则改进后的模糊PID控制性能进行仿真研究与分析。在AMESim中搭建阀控对称缸的液压系统模型,利用MATLAB的Simulink模块库,实现笔者所提控制器的设计,通过MATLAB自带的Fuzzy工具箱,完成对所设计的模糊规则库的编写与创建,借助2个软件的接口技术,实现一个完整的电液位置伺服系统的建模。

在AMESim中搭建的阀控对称缸的液压系统模型如图5所示。

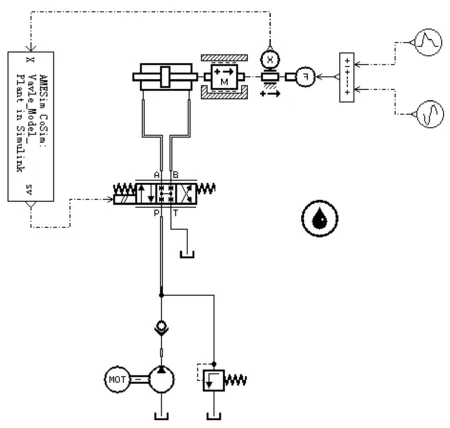
图5 阀控对称缸的液压系统模型

阀控对称缸系统主要参数如表3所示。

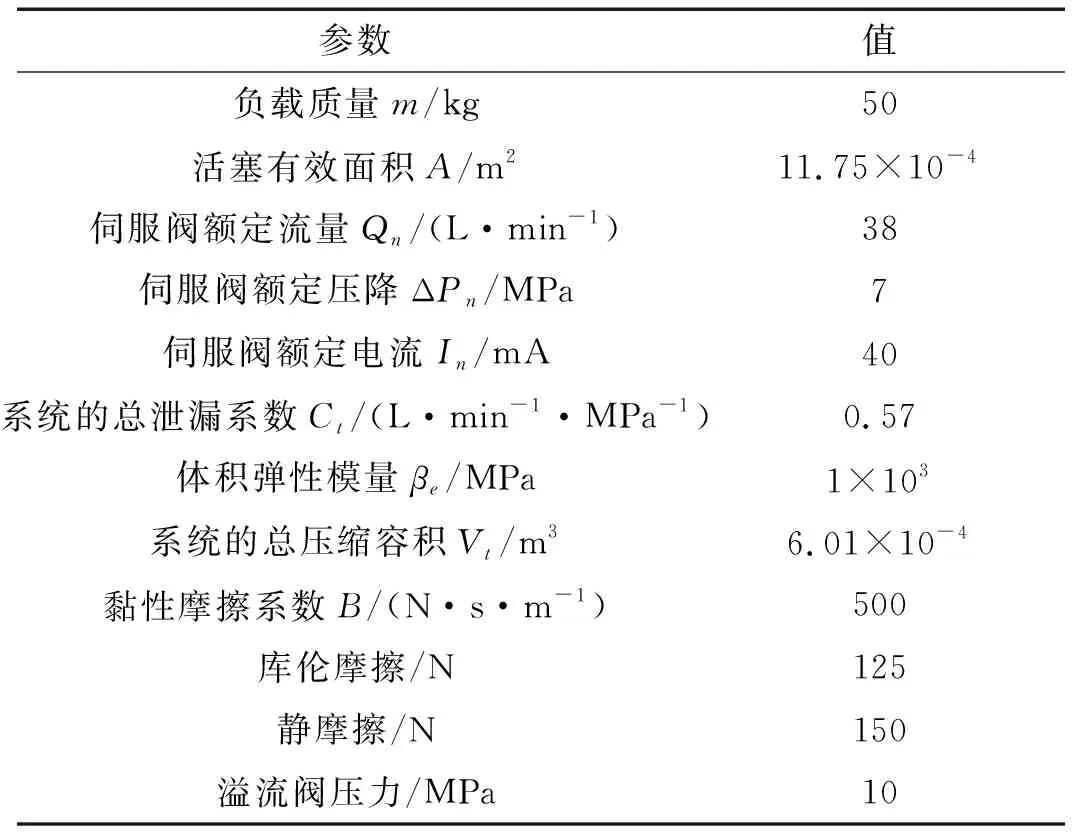
表3 阀控对称缸系统主要参数

在Simulink中搭建的改进模糊PID控制器的模型如图6所示。

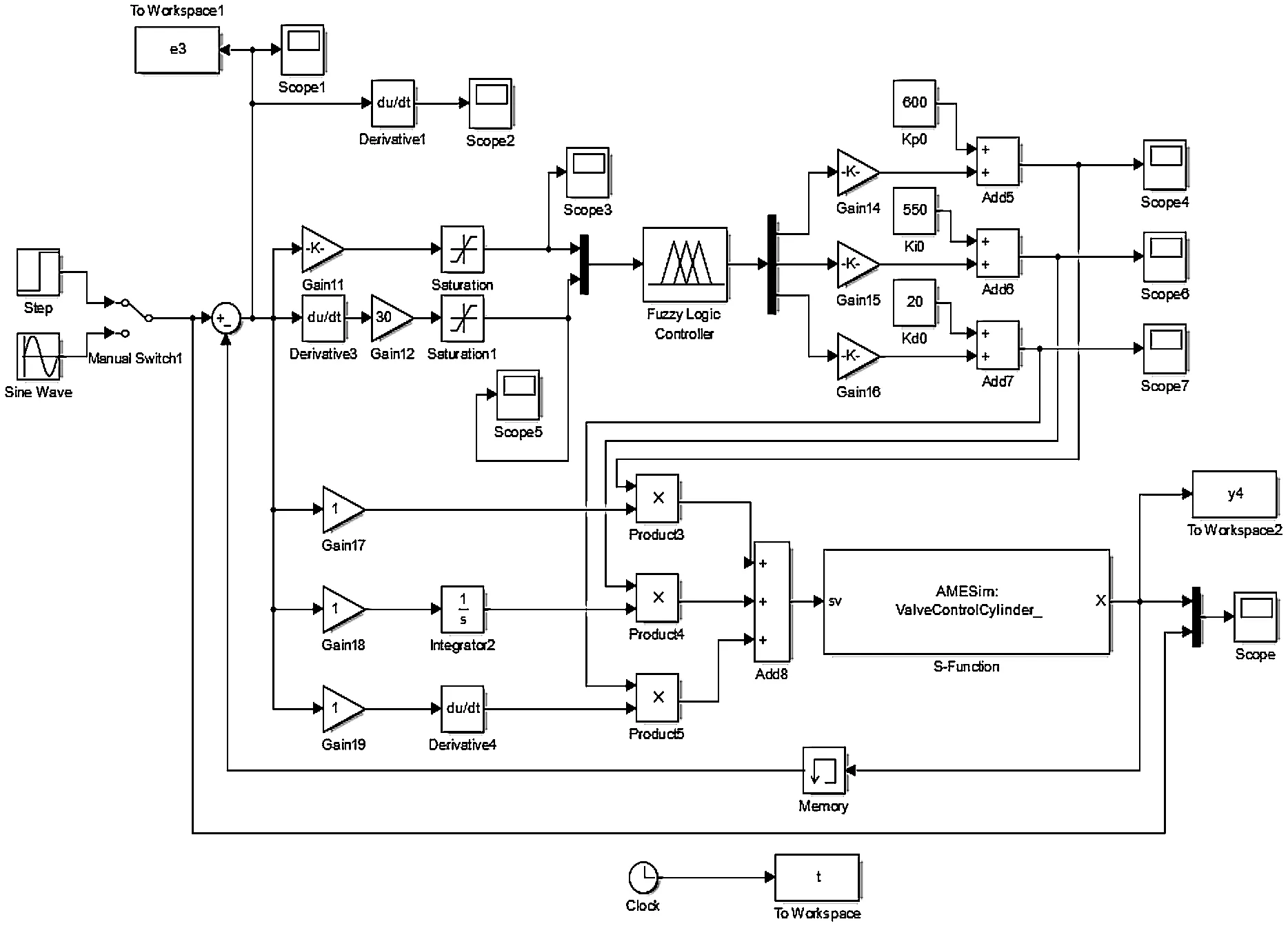
图6 改进模糊PID控制器模型

为检验规则改进后的模糊PID(FPID)控制器是否具有快速的响应能力,以及更好的位置跟踪精度和抗干扰能力,笔者以电液位置伺服阀控缸系统为被控对象跟踪阶跃信号,并与PID控制器和传统模糊PID控制器进行对比分析;

此外,为验证所设计的模糊PID控制器在系统的启闭过程中是否仍具有良好的控制效果,笔者以正弦信号来模拟系统的启闭过程,做了两组跟踪正弦信号的仿真研究,以进一步检验所设计控制器的优越性和可行性。

3.1 跟踪40 mm的阶跃信号

输入40 mm的阶跃信号,为模拟突变干扰的影响,假设在5 s时加入一个幅值为3 000 N的阶跃力模拟突变干扰。此时,系统位置跟踪曲线、动态跟踪误差曲线如图7所示。

图7 加入阶跃干扰力的阶跃响应

其中,PID控制的参数:P=600、I=550、D=20;模糊PID控制的参数:Ke=1 500、Kec=30,KΔp=100、KΔi=45.8、KΔd=1.67,Kp0=600、Ki0=550、Kd0=20。

从图7(a)可以看出:这3种控制方法均能实现对位置指令的精确跟踪,但跟踪精度与抗干扰能力有所差别。传统模糊PID控制和PID控制在1 s附近均出现不同程度的超调量,而改进模糊PID控制的超调量很小几乎没有;

此外,3种控制策略下系统达到稳态的时间也大不相同,改进模糊PID控制下系统在1.5 s处达到稳态,而系统在其余两种控制器作用下都是在2.8 s后才进入稳态;在5 s处加入突变干扰后,3种控制方案下系统均出现了波动,但改进模糊PID控制的波动情况明显小于其余控制算法,抗干扰能力更强。

从图7(b)可以看出:PID控制下系统的最大位置跟踪误差为给定指令的9.5%;传统模糊PID控制下系统的位置跟踪误差在5.5 s～6.1 s超过了给定指令的7.5%(最大为10.1%),其他时间段里的位置跟踪误差在给定指令的7.5%以内;而改进模糊PID控制下系统的最大位置跟踪误差仅占给定指令的5.2%,相比于PID控制器所设计的规则改进后的模糊PID控制器的最大位置跟踪误差缩小了45.26%,所设计的规则改进后的模糊PID控制器相比于传统模糊PID控制器,最大位置跟踪误差缩小了48.52%,系统动态跟踪误差明显小于其他两种控制方法。

由此可以得出结论,即与其余两种控制器相比,改进的模糊PID控制器响应能力更快、伺服跟踪精度更高、抗干扰能力更强。

3.2 跟踪1 Hz～40 mm的正弦信号

输入40sin(2πt) mm的正弦信号,为模拟实时变化的干扰力,0 s时加入3 000sin(2πt) N的干扰力,模拟时变干扰。此时,系统位置跟踪曲线、动态跟踪误差曲线如图8所示。

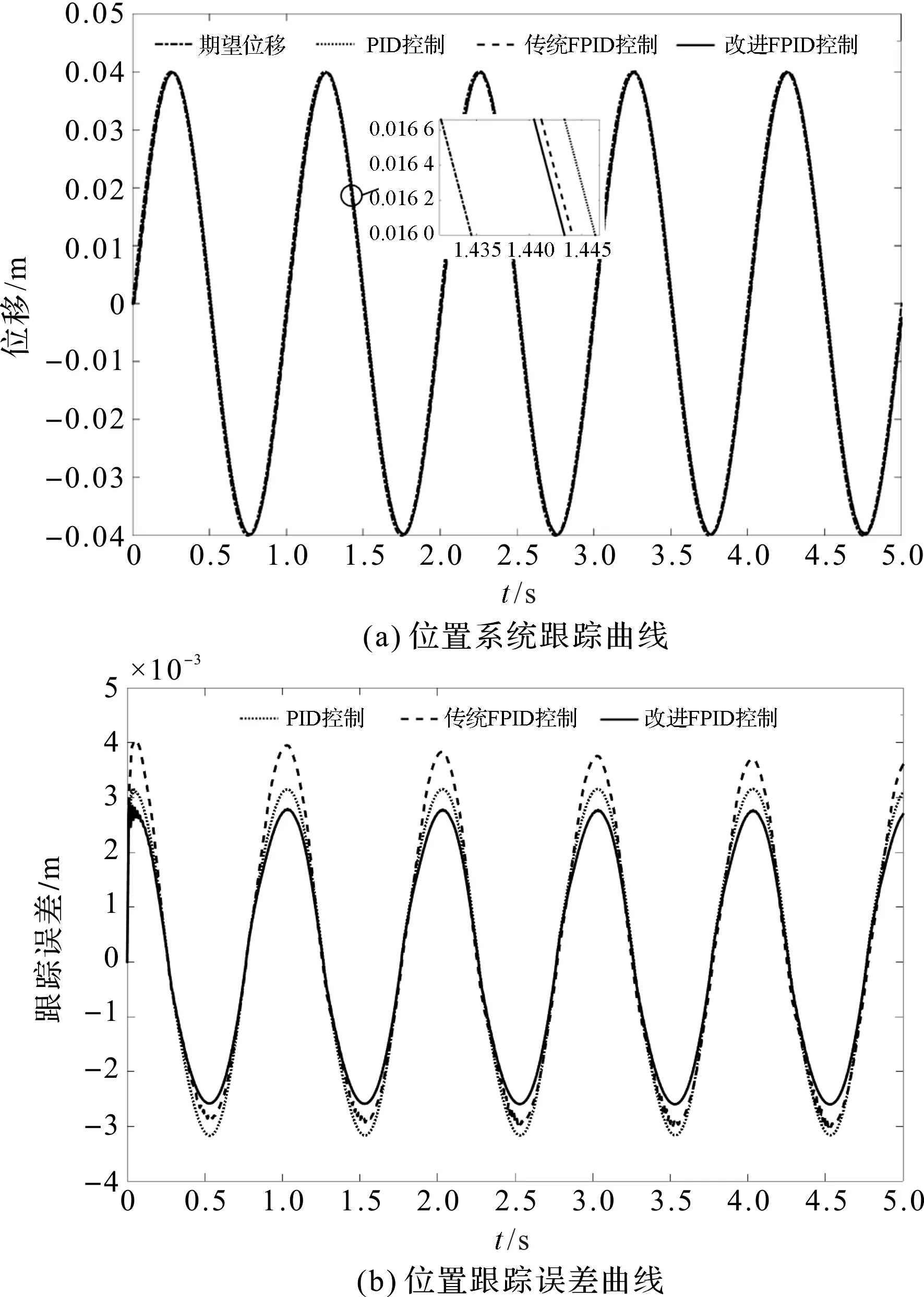
图8 加入正弦干扰力的正弦响应

其中,PID控制的参数:P=7 500、I=2 500、D=5;模糊PID控制的参数:Ke=1 500、Kec=30,KΔp=450、KΔi=208、KΔd=0.5,Kp0=7 500、Ki0=2 500、Kd0=5。

从图8(a)以及局部放大图可以看出:这3种控制方法均能实现对位置指令的精确跟踪并且都具有一定的鲁棒性,但改进模糊PID控制下系统的伺服跟踪精度优于其余两种控制方法。

从图8(b)可以看出:在加入时变干扰的情况下,PID控制器的最大跟踪误差为给定指令的7.95%;传统的模糊PID控制器的最大跟踪误差占给定指令的9.6%;而规则改进后的模糊PID控制器的最大跟踪误差仅为给定指令的6.47%,相比于PID控制器所设计的规则改进后的模糊PID控制器的最大位置跟踪误差缩小了18.62%,所设计的规则改进后的模糊PID控制器相比于传统模糊PID控制器,最大位置跟踪误差缩小了32.61%,系统动态跟踪误差明显小于其他两种控制方法。

由此可以得出结论：在系统的启闭过程中,所设计的规则改进后的模糊PID控制器仍具有良好的控制效果和抗干扰能力。

现实中干扰一般是复杂无规律的,因此为了使仿真更接近现实,同时为了进一步对比传统模糊规则库和改进模糊规则库对PID参数在线修正的灵活性和准确性,笔者用一组复合的干扰力来模拟复杂无规律的干扰,即将上述仿真中,将有规律的正弦干扰力改为复杂的复合干扰力。

此时,系统的动态跟踪误差曲线如图9所示。

图9 加入复合干扰力的正弦响应

其中,复合干扰力的函数表达式如下:

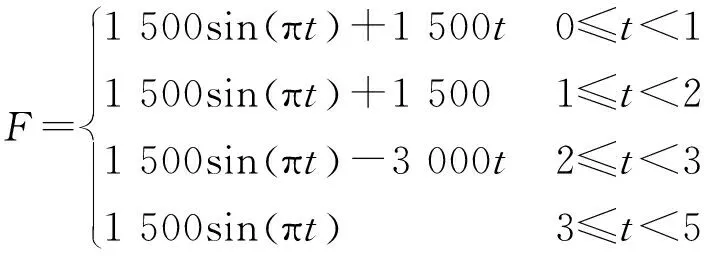
(2)

复合干扰力曲线如图10所示。

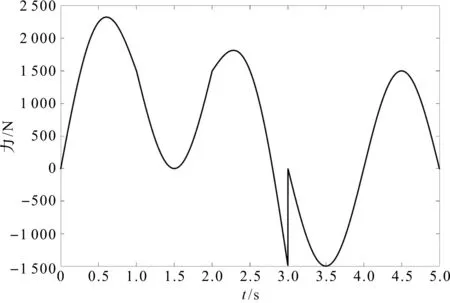
图10 复合干扰力

从图9可以看出:将正弦干扰力换为复合干扰力后,传统模糊PID控制在0.5 s、2.5 s、4.5 s均出现了不同程度的抖震现象,改进模糊PID控制在3 s处因干扰力的跳跃性变化而产生了轻微的抖震,但很快就趋于稳定,相比于传统模糊PID控制,其稳定性得到了显著提升;此外,改进模糊PID器控制下系统的动态跟踪误差明显依旧小于其他两种控制方法。

结合图8(b)和图9可以看出:在加入干扰的情况下,传统模糊规则库和改进模糊规则库均能实现对PID参数的在线修正,但修正能力有所差别,传统模糊规则库因存在精准度不足的问题而导致其正向跟踪误差大于PID控制器的正向跟踪误差,而改进模糊规则库克服了该问题,故改进模糊PID控制下无论是正向误差还是负向误差均比PID控制下的小。

由此可以得出结论,即所设计的规则改进后的模糊PID控制器的模糊规则库更符合PID的调整规律,对Kp、Ki、Kd进行调整时更加灵活与准确。

综上仿真结果可以说明:相比于传统的ΔKp规则库,改进后的ΔKp规则库更符合Kp的调整规律,对Kp参数进行调整时更加灵活与准确;故在系统发生扰动时,规则改进后的模糊PID控制器的响应更加迅速、抗干扰能力更强。

4 结束语

针对目前传统模糊PID控制算法存在精准度不足的问题,笔者提出了一种改进模糊PID算法,其核心是对传统模糊PID中的规则库进行修正,改进后的模糊PID智能控制策略综合了PID控制和模糊控制的优势,具有优异的伺服跟踪精度和抗干扰能力;为了验证改进方法的可行性和有效性,笔者通过Simulink搭建了新的模糊规则库,在此基础上完成了对改进模糊PID控制器的设计;最后以电液位置伺服阀控缸系统为研究对象,对所提控制策略进行了联合仿真。研究结论如下:

(1)笔者提出的改进模糊PID控制器统一了模糊控制与PID控制的优势,即解决了PID控制参数固定不变的问题,又可以使控制算法在系统数学模型未能精准创建的情况下,兼具优异的伺服控制性能和鲁棒性;

(2)与传统的模糊规则库相比,笔者所提的改进后的模糊规则库中的ΔKp规则库更符合Kp的调整规律,对Kp、Ki和Kd的参数进行在线修正时,显得更加灵活与准确,故更适合于PID控制参数的在线修正与自整定;

(3)联合仿真的结果表明:改进模糊PID控制器克服了传统模糊PID控制器存在的问题,其伺服跟踪精度和抗干扰能力都得到了显著的提升。

另外,在该控制策略中的优化ΔKp规则库思路,可以为将来模糊PID控制的改进与优化提供一条新的途径。