基于迁移成分分析的跨域轴承故障分类方法研究*

兰雨涛,胡超凡,金 京,王衍学*

(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.桂林电子科技大学 机电工程学院,广西 桂林 541004)

0 引 言

目前,滚动轴承的智能故障诊断技术发展迅猛[1-3],能够快速、高效地对故障进行识别分类。但是智能故障诊断方法存在一个重要的假定,即标记的训练数据和未标记的测试数据要服从相同的分布[4]5525。然而,该假定存在两个缺陷:(1)被标记的故障数据很难从一些机器中收集上;(2)用标记的数据训练的智能故障诊断算法识别未标记的样本,可能会因为标记和未标记的数据集是从不同机器上获取的,从而导致失败[5]。因此,源域和目标域间存在分布差异,并可造成重要的分类性能退化[4]5529-5530。换而言之,发现一个良好的跨域特性表示很关键。一个好的特征表示可以尽可能减少域间分布的差异,并能够保留原始数据的重要属性。

为了解决域分布问题,域自适应技术被构造出来[6]。域自适应算法通过域不变子空间特征,构造从源域到目标域的知识迁移[4]5526,该算法已经得到了成功的应用[7,8]。在学习域适应的公共特征表示方面,YANG S和ZHANG Y等人[9]基于串行自编码提出了新的表示学习框架,通过穿行连接两种不同类型的自动编码器,提取了更丰富的特征表示。SHEN J和QU Y等人[10]利用一个用于评判标识的神经网络估计源样本和目标样本之间的经验Wasserstein距离,并通过优化特征提取网络,以最小化估计Wasserstein距离,进而学习域不变特征表示。ZHAO H和COMBES RTD等人[11]描述了当边缘标签分布因源域到目标域不同时,学习不变表示和两个域上实现小联合误差之间的基本权衡。何志海[12]提出了一种对目标域特征分类具有一致性正则的非监督域自适应算法框架,从而提高了源域分类器对目标域特征分类的准确性。

但是,目前这些算法不能推广到样本外模式,且无法显著减小域间分布差异。迁移学习是近年来提出的一种新型机器学习方法,其通过用已获取的知识作为源域对目标域,或者说相关但有差异的问题进行求解。该算法可以处理难以获取训练样本的学习问题,并且已在文本识别[13]、图像识别[14]等领域得到初步的应用。

本文提出一种新的特征提取方法,其以迁移成分分析(TCA)算法[15]1187对域自适应算法进行优化;学习源域、目标域下的一组共同迁移成分,以便当投影到当下再生希尔伯特子空间子上时,使不同域的数据分布彼此接近,使源域、目标域的数据分布差异大大减小;基于迁移成分分析的域自适应来直接适应源域和目标域的特征表示,用于解决轴承智能故障诊断中的特征表示适应问题,并对轴承故障进行分类,完成对不同类型的轴承故障的识别。

1 域自适应和TCA理论基础

1.1 域自适应

由于源域和目标域数据分布不一、存在差异,源域的轴承故障诊断数据不能准确地辨识目标域轴承的未标记数据样本类别,致使滚动轴承的健康状态无法正确判断。

针对上述的域分布差异问题,本文将数据都映射到一个特征子空间中,并在特征子空间中找一个测量准则,使得源域和目标域数据的特征分布尽可能地接近,缩小分布差异。因此,基于源域数据特征训练出来的判别器,就可以用到目标域数据上,源域轴承的故障诊断知识可以进而辨识目标域轴承的健康状态。

诊断示意图如图1所示。

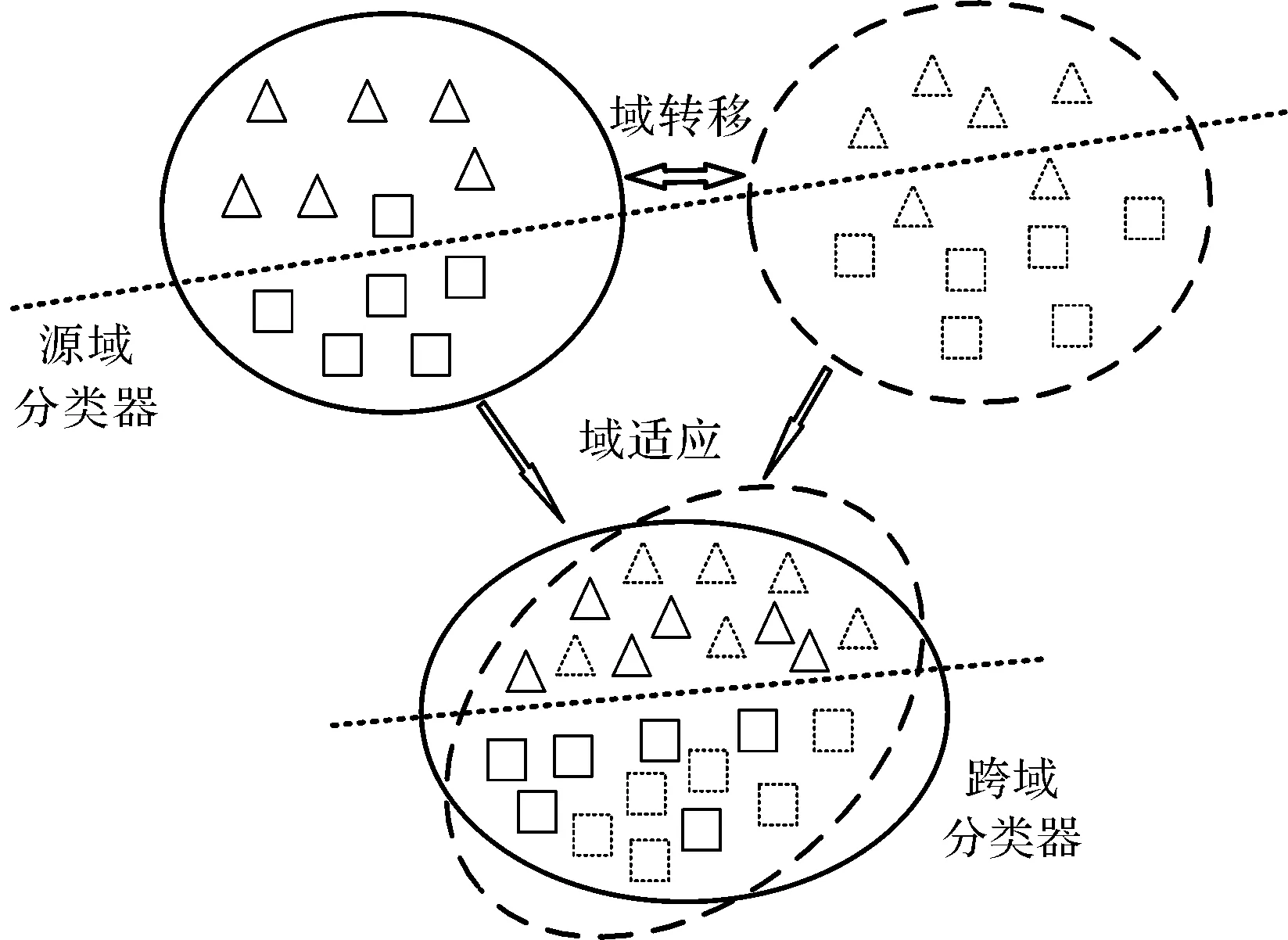
图1 故障数据迁移诊断示意图

基于目标域没有被标记的训练数据,但却有大量未被标记的数据的情况,此处假设:

DS(被标记的数据)在源域中是可用的;DT(未被标记的数据)在目标域中是可用的。

源域数据可以表示为:DS={(xS1,yS1),…,(xSn1,ySn1)}。

其中：xSi∈X—输入;ySi∈Y—输出。

目标域数据可以表示为:DT={xTn1,…,yTn1}。

让P(XS)和Q(XT)(简写为P和Q)分别成为XS和XT的边缘分布;然后,预测与目标域中的输入xTi对应的标签yTi。

一个典型的域自适应设置中关键假设是:

P≠Q,但P(YS|XS)=P(YT|XT)。

用最大均值差(MMD)作为基于再生核希尔伯特空间(RKHS)的分布比较的相关准则;让X={x1,…,xn1}和Y={y1,…,yn2}成为分布为P和Q的随机变量集。

P和Q之间距离的经验估计可被MMD定义为:

(1)

式中:H—通用的希尔伯特空间,φ:X→H。

因此,两个样本分布的距离可以通过两个样本映射到一个希尔伯特空间的均值之间的距离,并得到很好的估计。

1.2 迁移成分分析算法

基于:{xSi}—源域中的输入、{ySi}—源域输出,{xTi}—目标域中的输入,预测{yTi}—未知的目标域的输出。在域自适应中假设边际密度P(XS)和Q(XT)差异很大,为XS和XT找到一个共同潜在表示,其能保留变换后的两个域的数据配置。

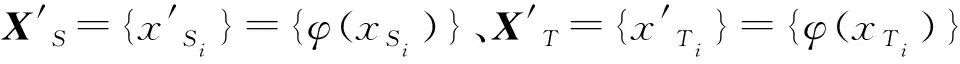
假设φ是由一个通用核产生的特征映射。如前文所示,两个分布P和Q间的距离可通过两个域的经验均值之间的距离进行测量[15]1188,即:

(2)

因此,最小化这个量可找到期望的非线性映射φ。凭借该方法的作用,式(2)中两个域的经验均值之间的距离可以被表示为:

(3)

其中:

(4)

式中:K—(n1+n2)×(n1+n2)核矩阵;KS,S,KT,T,KS,T—分别对应k在源域、目标域、跨域数据上定义的核矩阵。

在转换设置中,学习核k可以通过学习核矩阵K来解决。由此产生的核矩阵学习问题被表述为一个半定规划(SDP);然后将主成分分析(PCA)应用于学习核矩阵,去跨域寻找低维隐空间。

笔者提出了一种有效的方法[15]1189:基于核特征提取寻找非线性映射φ,学习核k可以直接推广到样本外模式。此外,笔者提出了一种使用明确的低阶表示的统一的核学习方法。

一般来说,m≪n1+n2,由此可得到核矩阵:

(5)

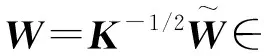
任意两个模式xi和xj之间对应的k的核可通过下式得出:

(6)

其中：kx=[k(x1,x),…,k(xn1+n2+x)]T∈(n1+n2)。

(7)

1.3 迁移成分提取

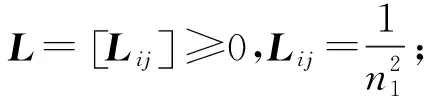
经过式(7)的最小正则化表示,域自适应的核学习问题降至:

s.t.WTKHKW=I

(8)

式中:μ—权衡参数;I∈m×m—单位矩阵;中心矩阵;In1+n2∈(n1+n2)×(n1+n2)—单位矩阵。

其中:I∈n1+n2所有列向量均为1。

通过跟踪优化问题,式(8)可以重新表述为:

(9)

or

(10)

证明:式(8)的拉格朗日量为:

tr(WT(I+μKLK)W)-tr((WTKHKW-I)Z)

(11)

式中:Z—对称矩阵。

将式(11)的导数w.r.t设为零,可以得到:

(I+μKLK)W=KHKWZ

(12)

在等式两边矩阵的左侧各乘以WT,然后将其代入到式(11)获得式(9)。因为矩阵I+μKLK是非奇异的,得益于正则化项tr(WTW),由此可以得到一个等价迹最大化问题(10)。

式(10)中W的解是对应于(I+μKLK)-1KHK的m个前导特征值的特征向量。因此,所提出的方法即被称为迁移成分分析(TCA)。

2 轴承故障的跨域特征迁移

本文方法主要由域自适应和TCA算法组成。该方法通过让源域和目标域样本在特征子空间上的最大均值差异最小化,从而得到一个降维的特征子空间。源域和目标域间的分布差异在这个子空间内减小,故而实现故障知识的跨域迁移。

具体来说,先获取滚动轴承的振动信号,将已知工况的滚动轴承振动信号作为源域样本,未知工况的轴承振动信号作为目标域样本;利用TCA算法处理源域样本和目标域样本的差异性,从而增加源域数据样本和目标域样本的相似度;通过最大均值差嵌入的判别可以迁移的源域数据,解决目标域中被标记数据供应不足即实际故障样本较少的问题,形成基于域自适应的迁移学习轴承故障诊断模型。

由此,源域的轴承故障知识可以用来识别目标域中未知的轴承故障类别。

在轴承故障诊断时,用笔者所提出的方法的诊断流程如图2所示。

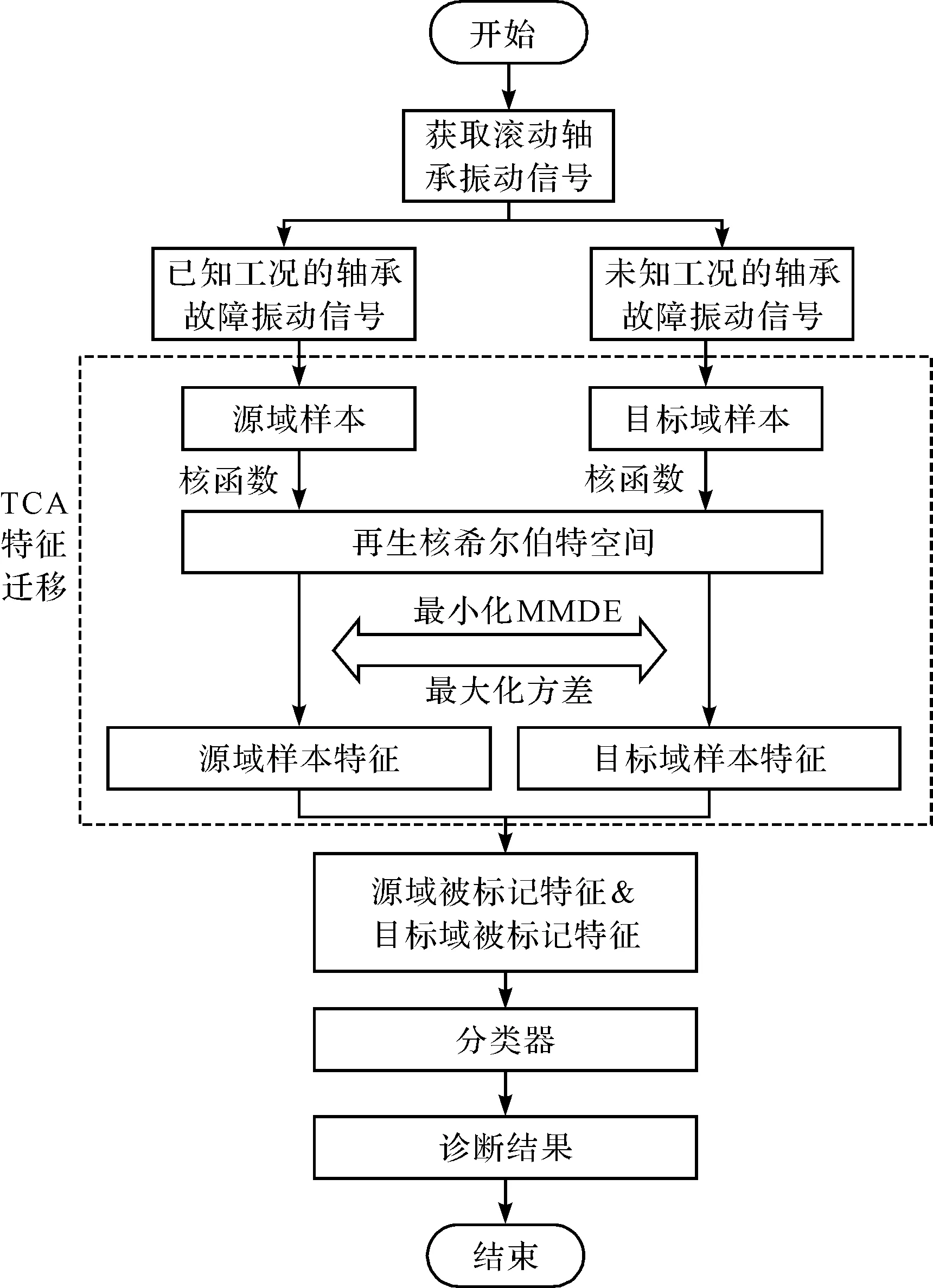
图2 迁移成分分析故障诊断结构图

3 实验验证与结果分析

3.1 实验数据

本文研究中的数据集由桂林电子科技大学的MFS试验台和凯斯西储大学(CWRU)提供。

轴承的4种不同健康状态包括外圈故障(OF)、内圈故障(IF)、滚动故障(BF)和正常(N)状态。本文研究中含有两种故障的尺寸大小分别为0.007 in与0.001 4 in。此外,使用的故障振动信号是通过两种电机负载0 HP、1 HP获得的。所以,基于本文设定的4种健康状态,一共有8种轴承工况。

用所提算法对每种不同故障尺寸数据提取特征,以验证所提出的基于迁移成分分析的域自适应轴承智能故障诊断技术的有效性。a数据训练b测试;反之,b进行训练a测试。

实验的迁移任务包括AB、BA、CD、DC、EF、FE、GH、HG。其中,TAB表示以故障尺寸为0.007 in的滚动体作为源域,以故障尺寸为0.014 in的滚动体作为目标域。反之,TBA则以故障尺寸0.014 in为源域,0.007 in为目标域。

类似地,TCD、TDC、TGH、THG依照相似的模式;其中,TEF、TFE表示正常状态下0 HP负载和1 HP负载互为源域和目标域。在源域的迁移任务中获得标记的样本数据,同时在目标域的每种对应工况下获得未标记的样本数据。

在两种故障尺寸和两种载荷下,8种提取时域信号后的跨域轴承故障分类任务,如图3所示。

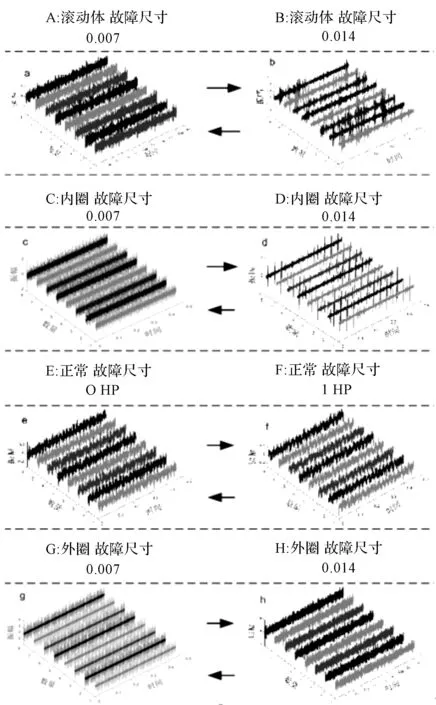
图3 4种健康状态下的跨域故障分类任务

3.2 基于GUET数据集的跨域故障分类结果

在本小节中,将采用GUET数据集来验证所提出的方法。具体来说,横向比较的方法包括JDA(joint distribution adaptation)和SVM(support vector machine)。

为了验证所提出方法的有效性,笔者挑选了迁移任务TAB和TFE进行分析。选择迁移任务TAB和TFE是因为在此两项任务中,本文所提出的方法获得了远高于其他两种对比方法的分类效果。

迁移任务TAB预测标签与实际标签关系,如图4所示。

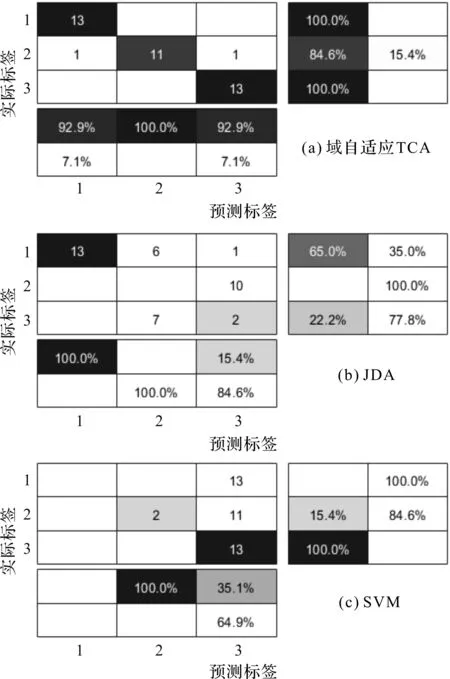
图4 迁移任务TAB预测标签与实际标签关系图

迁移任务TFE预测标签与实际标签关系,如图5所示。

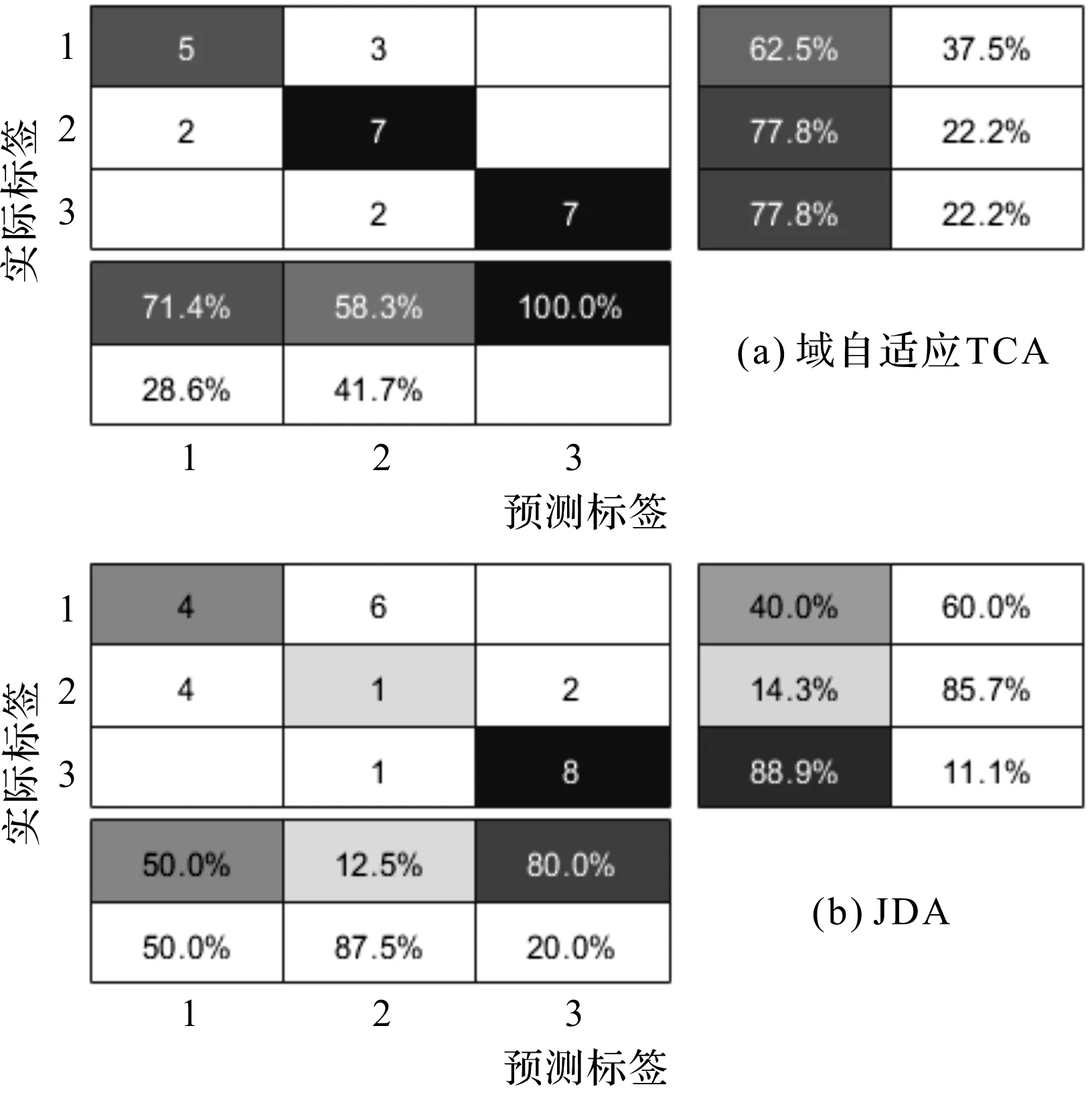
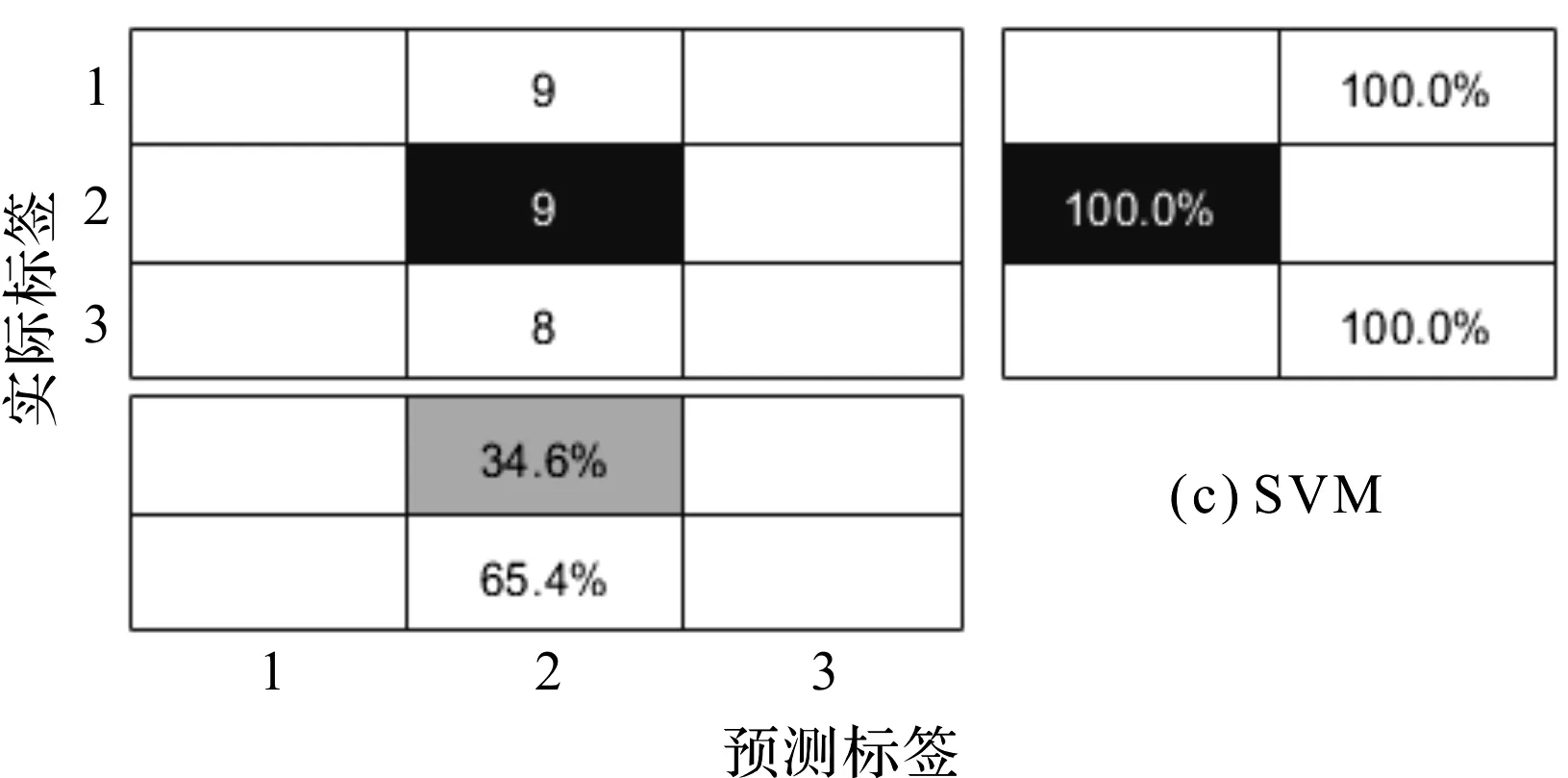
图5 迁移任务TFE预测标签与实际标签关系图

图(4,5)中,每个模糊矩阵共有3组数据,每行分别代表滚动体、内圈和外圈数据。横向为预测标签的分类,竖向为实际标签的跨域分类。其中，黑色与灰色为正确分类,白色为错误分类。为了直观对比本文所提方法的分类效果,此处一并列出了其余两种对比方法的分类模糊矩阵。

从图4所表示的3种方法下的TAB任务所对应的模糊矩阵可以观察到:

本文提出的域自适应TCA跨域分类技术的测试准确度能够达到95.27%,预测标签的测试精度也达到了94.87%;而JDA的跨域测试精确度只有38.47%,SVM的跨域测试精确度也仅为45.03%;

图4(a)所代表的本文所提方法的分类精度,无论在实际标签还是在预测标签上的测试精确度,都远远优于图4(b,c)中的两种方法。

本文所提方法,同样可以在图5的迁移任务TFE中观察到如迁移任务TAB同样优越的分类效果。本文技术的测试准确度可以达到76.57%,而JDA的跨域测试精确度为47.5%,SVM的跨域测试精确度过差只有11.53%;同时,每一组的分类精确度也比对比方法优越。JDA和SVM的精度仅在个别组预测标签上表现尚可,但是总体平均精度效果稍差。本文提出的分类技术在3种预测和实际标签的分类精度均优于所列的对比方法。

从图(4,5)还可以看出:所提出的基于迁移成分分析(TCA)的域自适应方法,不但能够对经过训练的滚动轴承样本跨域特征之间的分布差异进行有效地处理,而且能够扩大类别之间可迁移特征的距离。

根据图(4,5)所示的结果表明:提出的方法能比其他方法对跨域迁移任务的目标域进行更有效、更精确的分类,能够进一步地拓展诊断机械装备各类故障。

3.3 基于西储大学(CWRU)数据集的跨域分类结果

为进一步验证所提方法的有效性,此处笔者采用来自凯斯西储大学(CWRU)的典型的benchmark跨域对象识别数据集,来验证笔者所提的方法。

与GUET数据集相同,CWRU含有同样8种迁移任务,本小节挑选了迁移任务TBA进行分析,如图6所示。

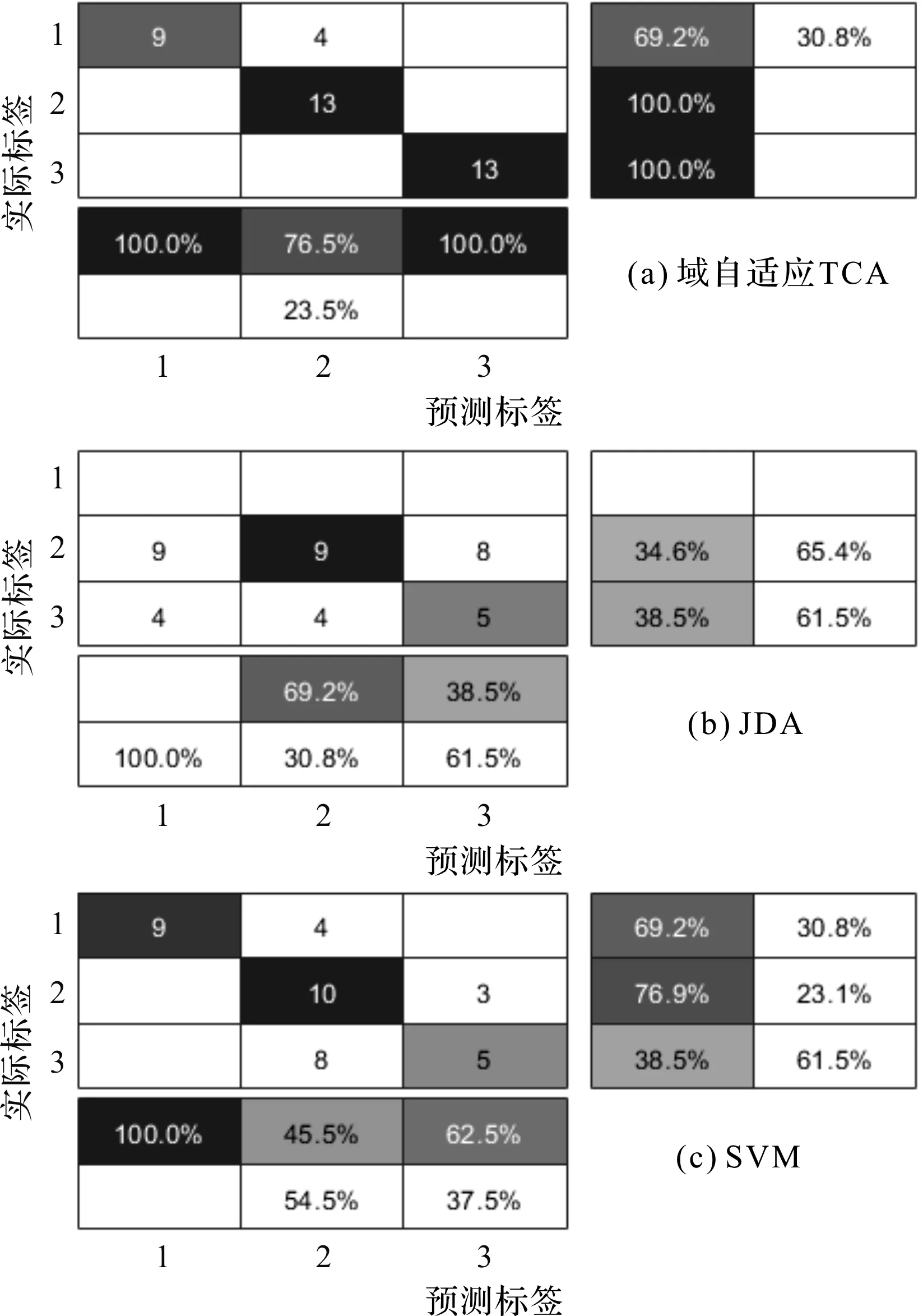
图6 CWRU迁移任务TBA预测标签与实际标签关系图

图6中,所提技术的分类准确度为92.17%,同时JDA与SVM的测试精确度仅为35.9%和69.33%。该结果清楚地展示了所提方法比其他方法能够更精确、有效地对目标域中的迁移任务进行分类,识别故障类别。

笔者使用t-SNE方法进一步对所提方法与对比方法的差异性进行定性分析,将跨域学习过程可视化,提取的故障特征被呈现在二维平面。

迁移任务TBA故障特征分布散点图如图7所示。

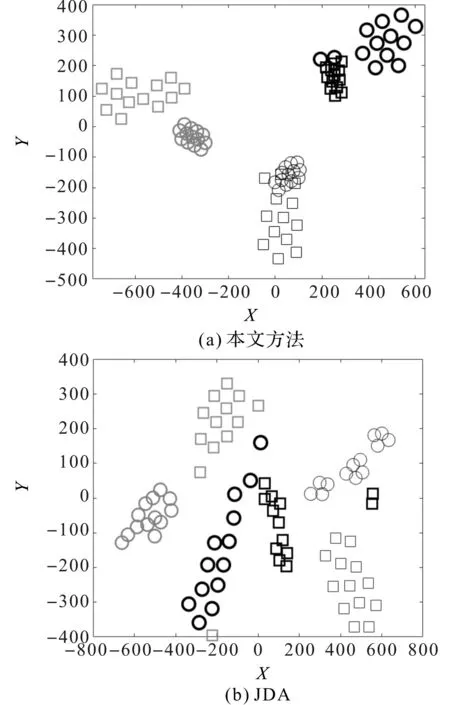
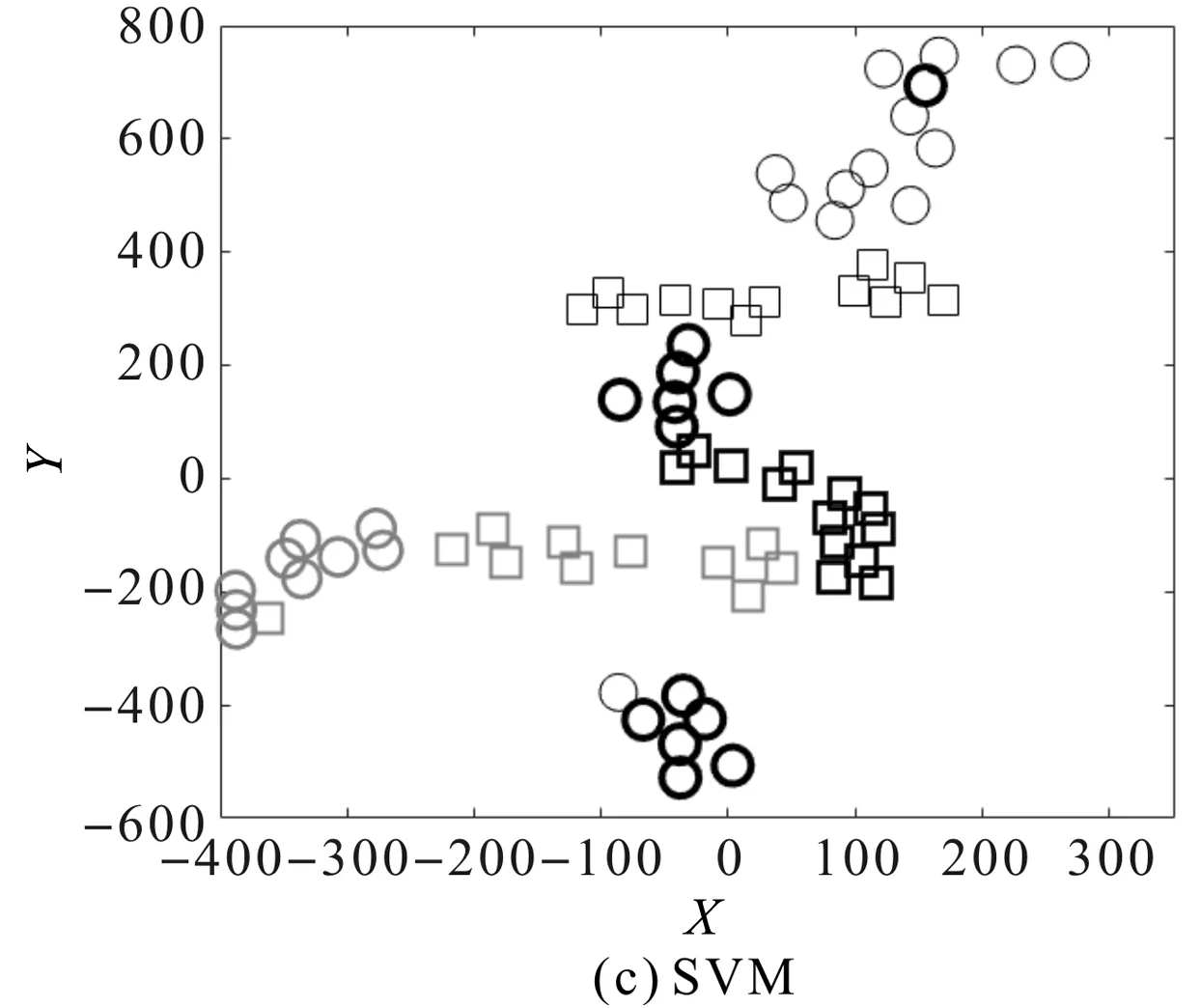
图7 迁移任务TBA故障特征散点分布图

从图7(a)可知:相对于图7(b,c)所展示的对比方法,本文方法扩大了不同健康类别间可迁移特征的距离,缩小了源域和目标域故障特征的分布差异,减小了测试集和训练集之间的分布差异对轴承诊断的影响;与图7(b,c)的对比方法相比,所提方法在将各故障类别有效分离的同时,也将同种工况样本更好地汇集在一起。

迁移诊断精度对比图如图8所示。

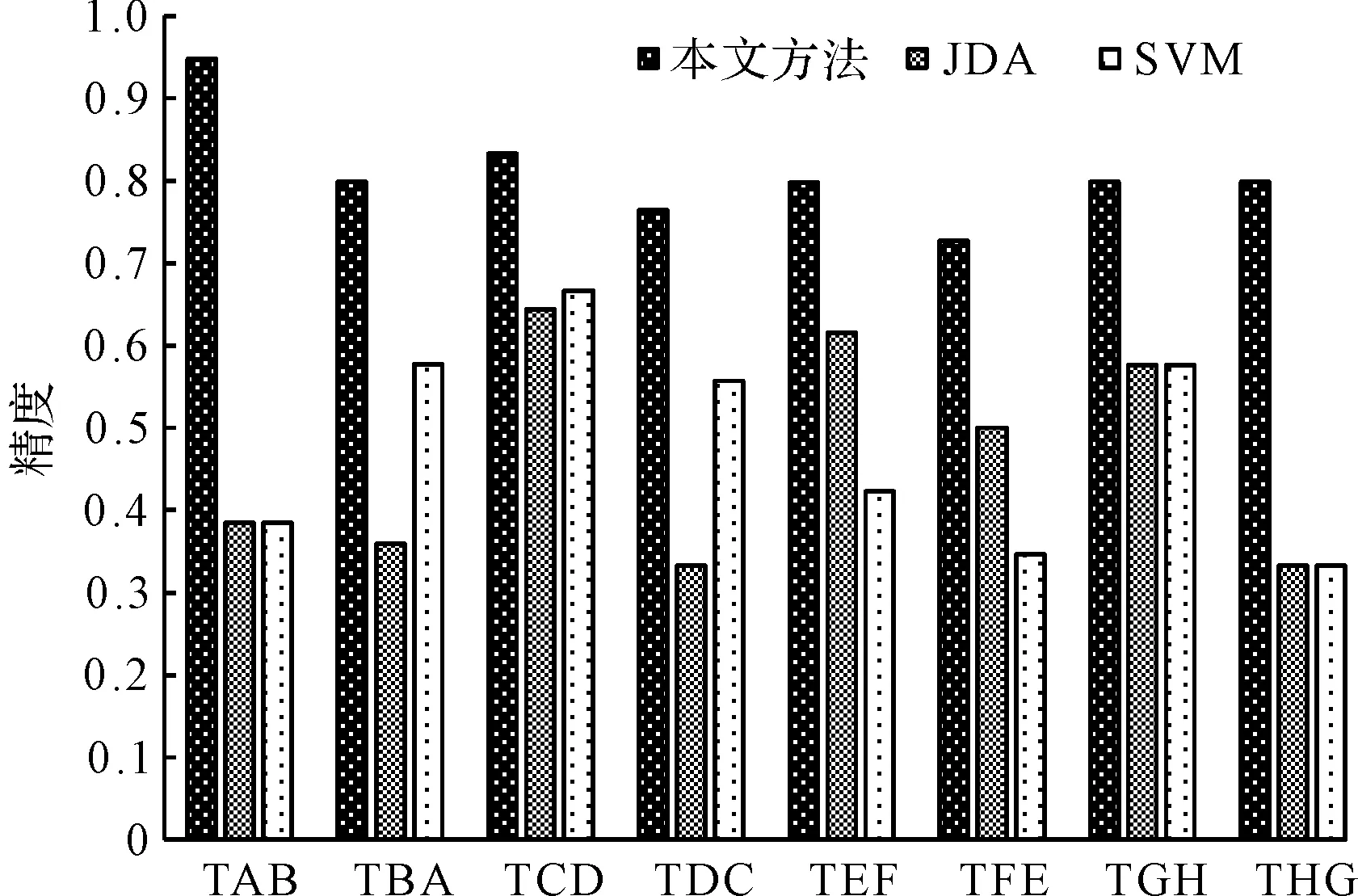
图8 迁移诊断精度对比图

从图8不同方法的对比条形图可看出:本文所提方法拥有最高的分类准确度,是3种故障分类方法中最高的;本文提出方法的跨域分类效果比其余两种方法更加优越;所提出的方法在8种跨域轴承故障分类任务中均获得了最高的测试准确度。

该结果主要因为:本方法通过迁移学习能够将来自源域的样本数据迁移至目标域中,从而克服了由目标域样本数据少或难以获取目标域故障样本,而造成的故障识别率低的缺陷。

8种迁移学习任务的分类准确度如表1所示。

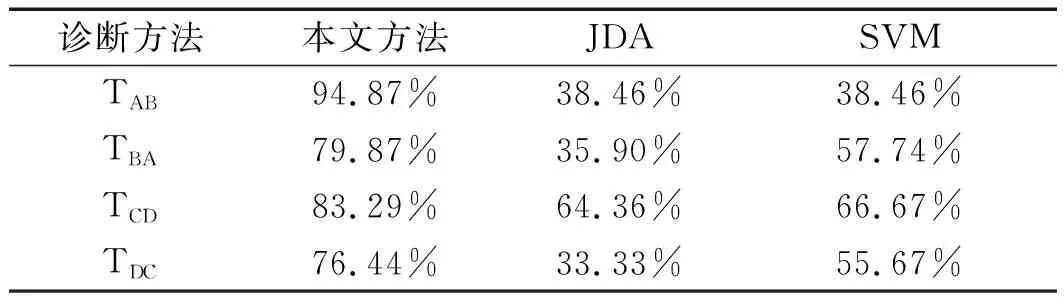
表1 8种迁移学习任务的分类准确度

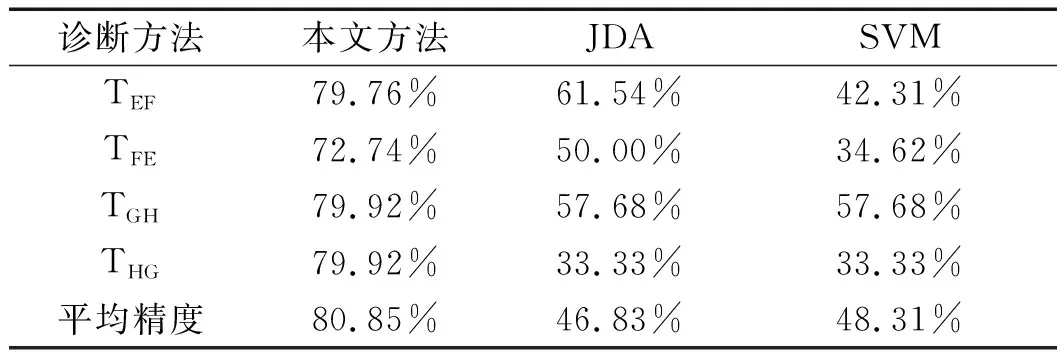
(续表)

由表1可以看出3种不同方法分类精确度进行比较的实验结果:

本文提出方法的平均测试准确度达到了80.85%,而其余两种对比方法因无法解决严重的域分布差异问题,缺乏故障样本的迁移过程,不能从目标域中提取更好的特征等原因,导致SVM的平均测试准确度为48.31%;而JDA的分类准确度仅仅为46.83%。

通过定量分析可看出:本文方法在每一种故障分类任务中的分类精度均大于两种对比方法。总的来看,本文通过基于TCA的域自适应方法所实现的分类精度要比其余对比方法优越很多。

4 结束语

本文提出了一种新的基于迁移成分分析的域自适应方法,用于轴承的跨域智能故障诊断,以及在标签数据难采集或可用数据稀少时,识别旋转机械装备的健康状态。

研究结论如下:

(1)本文方法能够实现域间,即不同工况下,轴承样本数据的迁移学习;通过寻找共同成分进行迁移学习,增加域间数据集的相似度,进而解决了测试样本与训练样本需要满足独立同分布要求的缺陷;

(2)所采用的方法适应小样本分类,显著提升了轴承健康状态的分类准确度;提出方法的最高分类精度达到95%,平均准确度达到了81%,比常用分类方法的准确类提升了70%左右。

通过与其他诊断方法的对比实验,验证了所提出方法的优越性和有效性,能够高效地辨识轴承的健康状态,完成对不同类型的轴承故障的识别。