细长类结构零件的高速铣削工艺参数优化研究*

赵涓涓,庞 博

(1.山西工程职业学院 机械电子工程系,山西 太原 030009;2.内蒙古工业大学 工程训练中心,内蒙古 呼和浩特 010051)

0 引 言

近年来,随着航空工业的发展突飞猛进,航空结构件逐渐面向精密化、整体化方向发展,尤其是在飞机产品制造业中,结构件作为其主体框架,对其他零部件起到支撑的作用,它的设计效率与质量直接影响到飞机的整体设计与制造[1]。

众多的大型结构件需要进行切削加工,每个零件从毛胚到成品又要被切除70%～90%的材料。长桁零件属于狭长类工件[2],在飞机结构中大量运用,承受着飞机的大部分升力和惯性载荷,同时也对飞机蒙皮起一定的支持作用[3]。由于受到制造技术和能力的制约,目前我国每年生产的飞机总量很少,其中,整体结构件的制造周期远远落后于国外水平,主要在于对加工工艺参数选择缺乏理论依据,不能充分利用先进机床的高效性能,加工效率低。

目前,有关于铣削过程中工艺参数优化的研究,主要考虑铣削过程运动学或静态切削力约束的工艺参数优化,如刀具路径优化[4]、进给率优化[5]的研究等。而对于基于加工过程动力学模型的工艺参数优化的研究则相对较少。

在早期的研究中,KURDI M H等人[6]提出了基于时域的有限元分析法,并进一步探讨了基于时域有限元分析法的材料去除率和加工误差(SLE)同步优化问题[7]。张金峰等人[8]利用三轴联动精密铣削机床加工了微细直沟槽,并选取了主轴转速、轴向切深、进给速度和刀具跳动量为研究因素,采用多因素正交实验和极差分析法对表面粗糙度值进行了数值分析。秦国华等人[9]提出了以最小的刀具磨损为目标,建立了铣削工艺参数的优化模型及其遗传算法的求解技术。

在结构设计中,有限元方法(FEM)对结构动态响应特性的识别和分析较为准确[10]。吴石等人[11]通过对刀具不同磨损状态下的切削力系数辨识,研究了铣刀磨损对铣削颤振稳定域及表面位置误差的影响。

很多学者对切削稳定性的研究主要聚焦在不同加工状态,或不同加工系统切削稳定性区域的预测及其影响因素的分析,未能充分运用有限元精确建模,预测工艺系统在不同加工阶段的动力学特性,并与实验状态相对应。

鉴于此,本研究将分别采用试验模态分析方法和有限元模态分析方法,获得刀具系统和工件系统的动力学特性参数,通过建立典型长桁零件在不同加工阶段、不同加工位置的有限元模型,研究其动力学特性变化规律。

1 基于动态铣削过程的工件系统动力学建模与稳定性分析

1.1 仿真条件

基于细长类航空结构件占用工时较长的典型加工工步,笔者建立典型工步下长桁件有限元模型,如图1所示。

图1 典型长桁结构件

以加工二工位粗铣缘板间余量为例,加工示意图如图2所示。

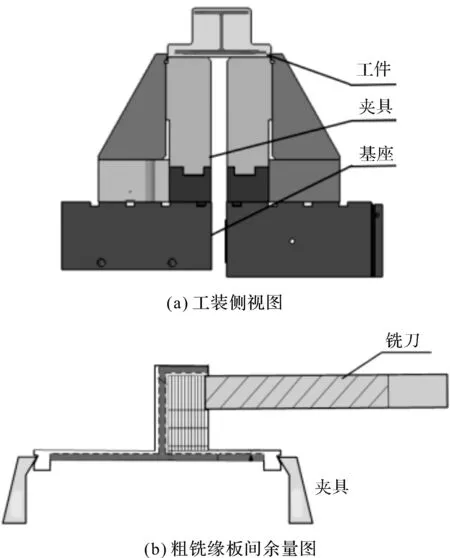
图2 粗铣缘板间余量目标优化工步的加工示意图

由图2可知,在二工位工况下,采用专用气动夹具夹紧工件,刀具选用25 mm的整体立铣刀,刀具悬伸量为100 mm,摆90°,顺铣加工,加工材料为铝合金。此处根据经验设定主轴转速为16 000 r/min,进给速度为10 m/min;刀具轴向加工余量17.4 mm,刀具径向加工余量49.11 mm;加工仿真时间为12 min。

1.2 长桁零件有限元精确建模

针对二工位下3.4 m典型长桁零件,笔者建立夹具中心距为1 m的典型长桁仿真模型,如图3所示。

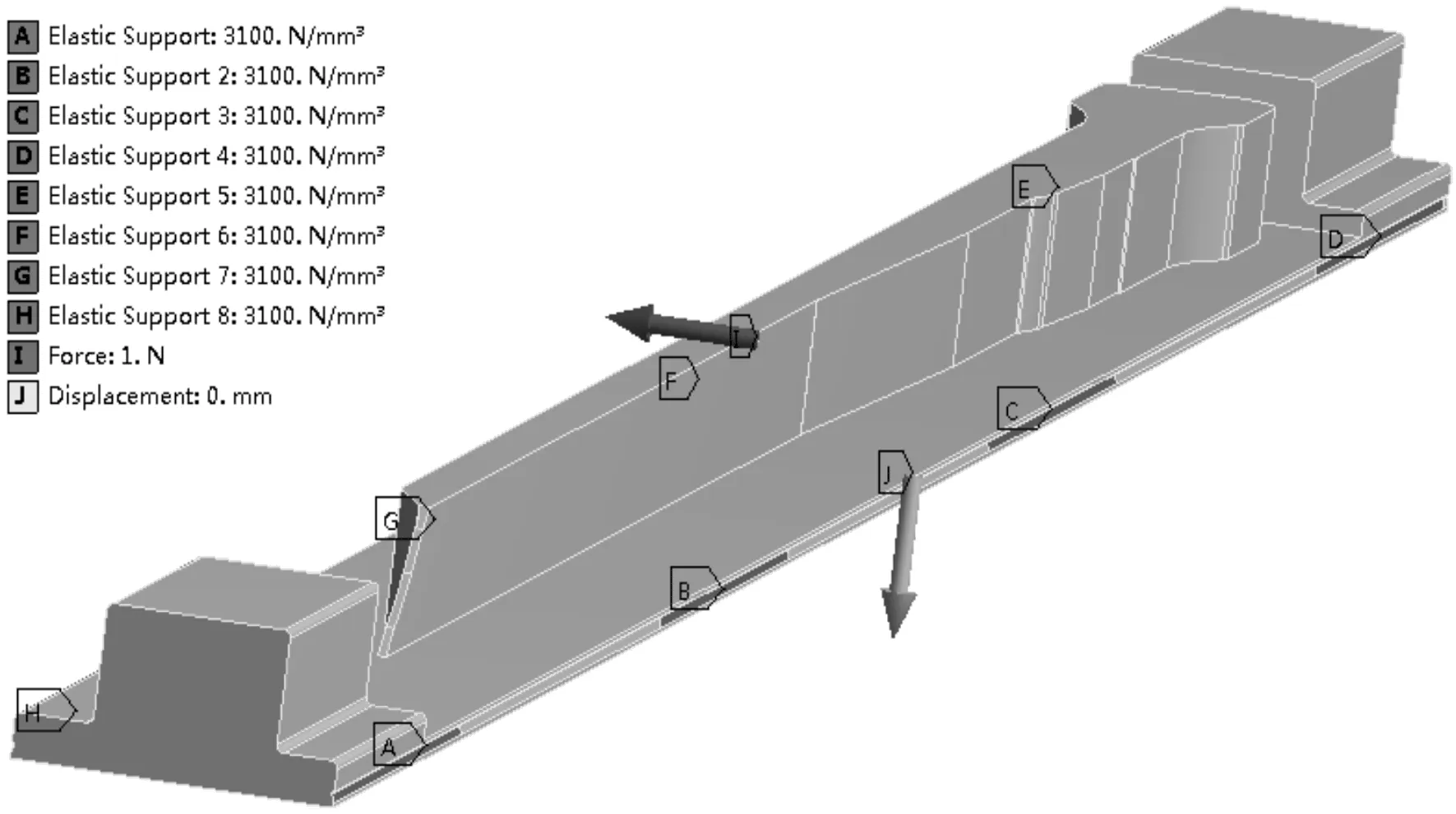
图3 某长桁粗铣缘板间余量时整体模型弹性模量E=85 GPa,泊松比为0.3

笔者采用有限元软件ANSYS Workbench[12]建立了工件系统动力学模型,对其进行了模态分析和谐响应分析,得出了相应工位下长桁零件系统仿真模型的固有频率和振型,预测了工位不同加工阶段下不同切削点的频率响应。

基于长桁零件仿真模型得到的不同切削点频率响应,如图4所示。

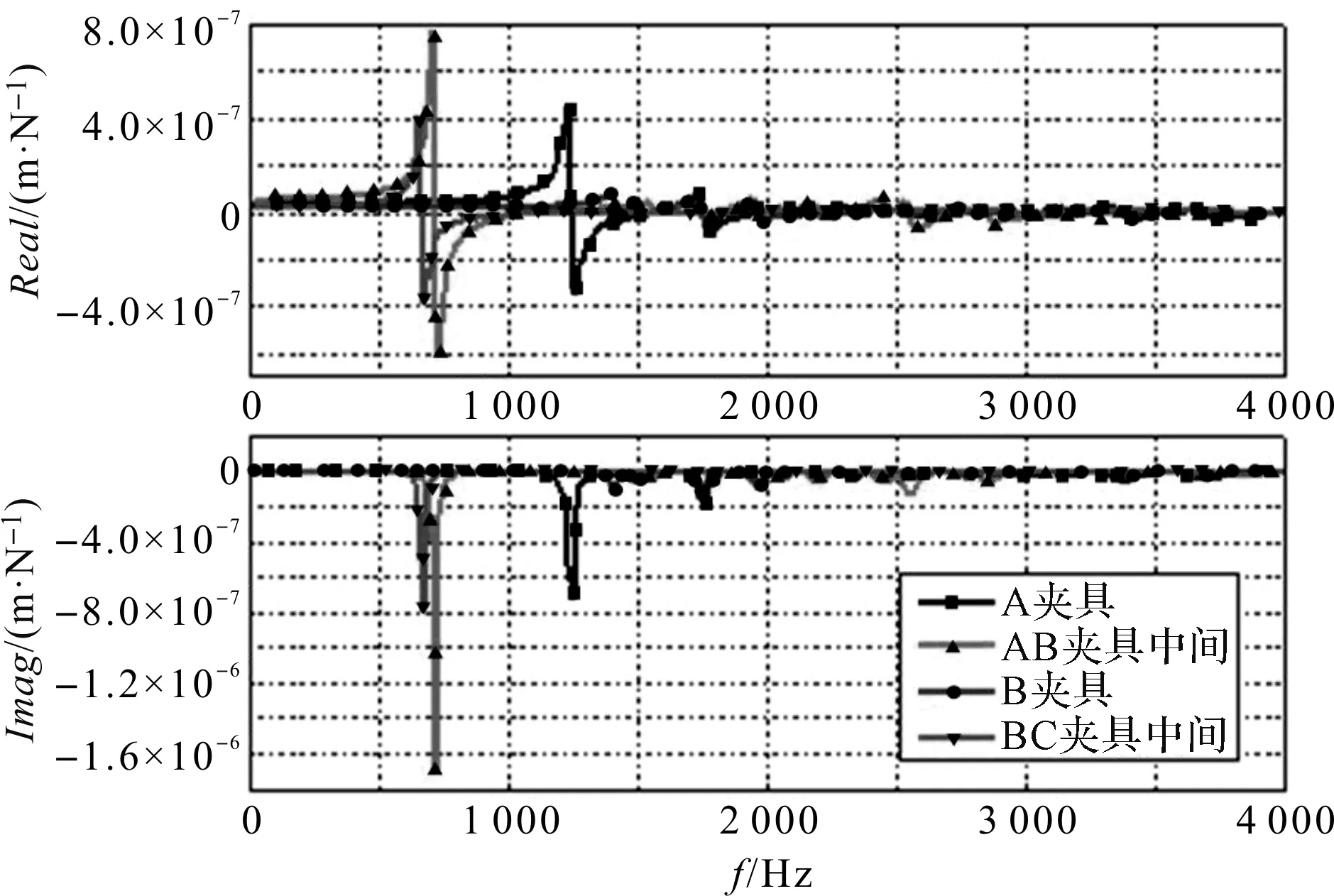
图4 粗铣缘板间余量长桁模型不同切削点的频响

工件在各实测位置的模态参数计算结果如表1所示。

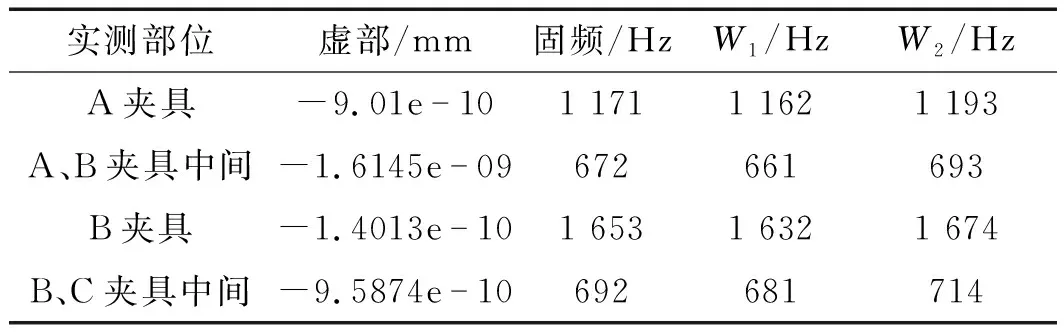
表1 工件各个实测部位模态参数

由图4和表1可知,通过动力学建模与分析识别了工件系统在不同实测位置的模态参数,该结果可为下一步进行长桁零件工艺系统的铣削稳定性分析提供依据。

1.3 铣削稳定域分析

经仿真后获得了不同加工位置下的工件系统频响,预测铣削稳定域如图5所示。

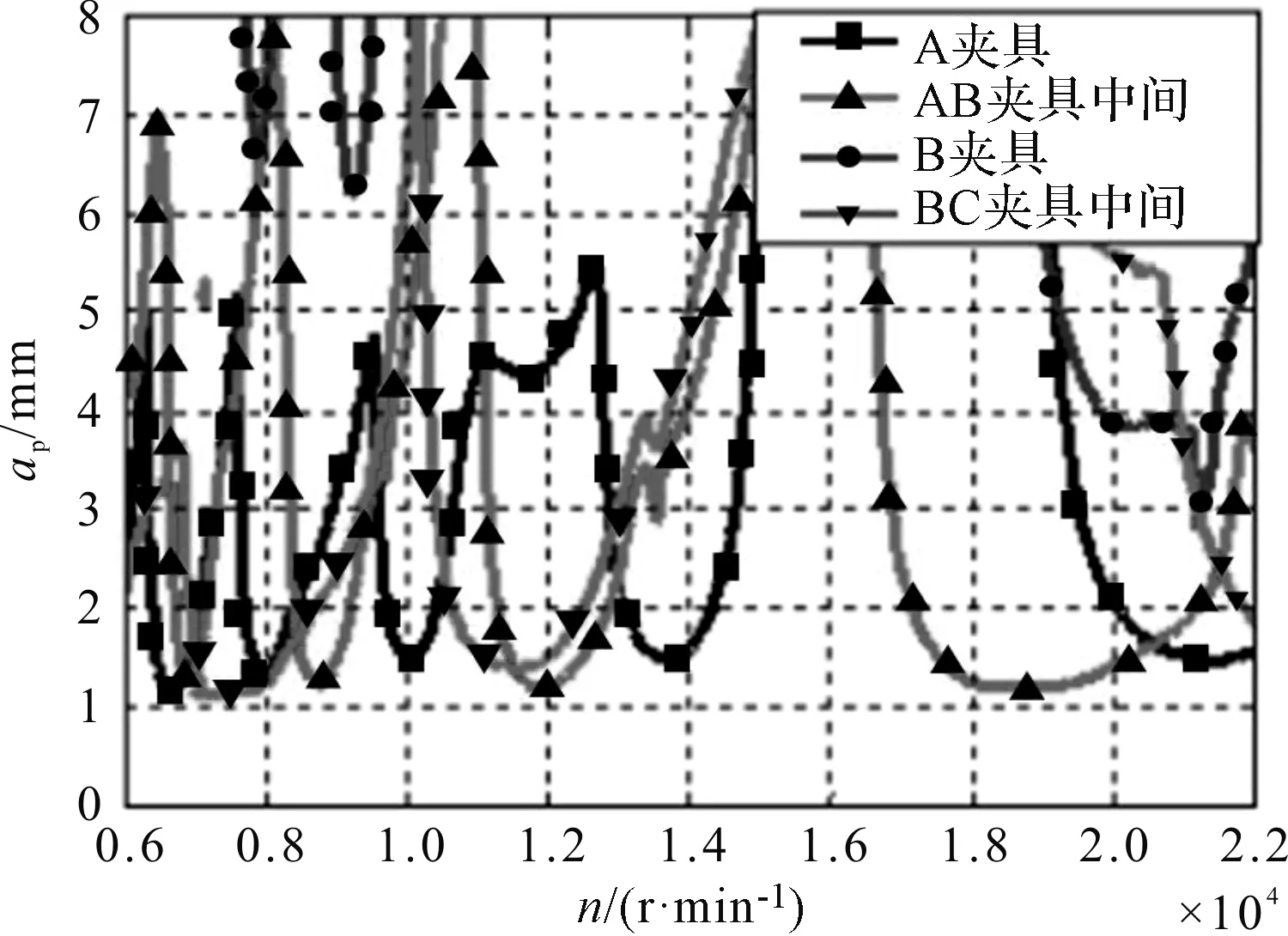
图5 长桁模型不同夹具中间的叶瓣图

由图5可知,优化后的铣削参数为:主轴转速n为16 000 r/min;进给速度Vf为10 m/min,刀具轴向加工余18.4 mm,刀具径向加工余量52.11 mm。

粗铣缘板间余量优化后的工序简图如图6所示。

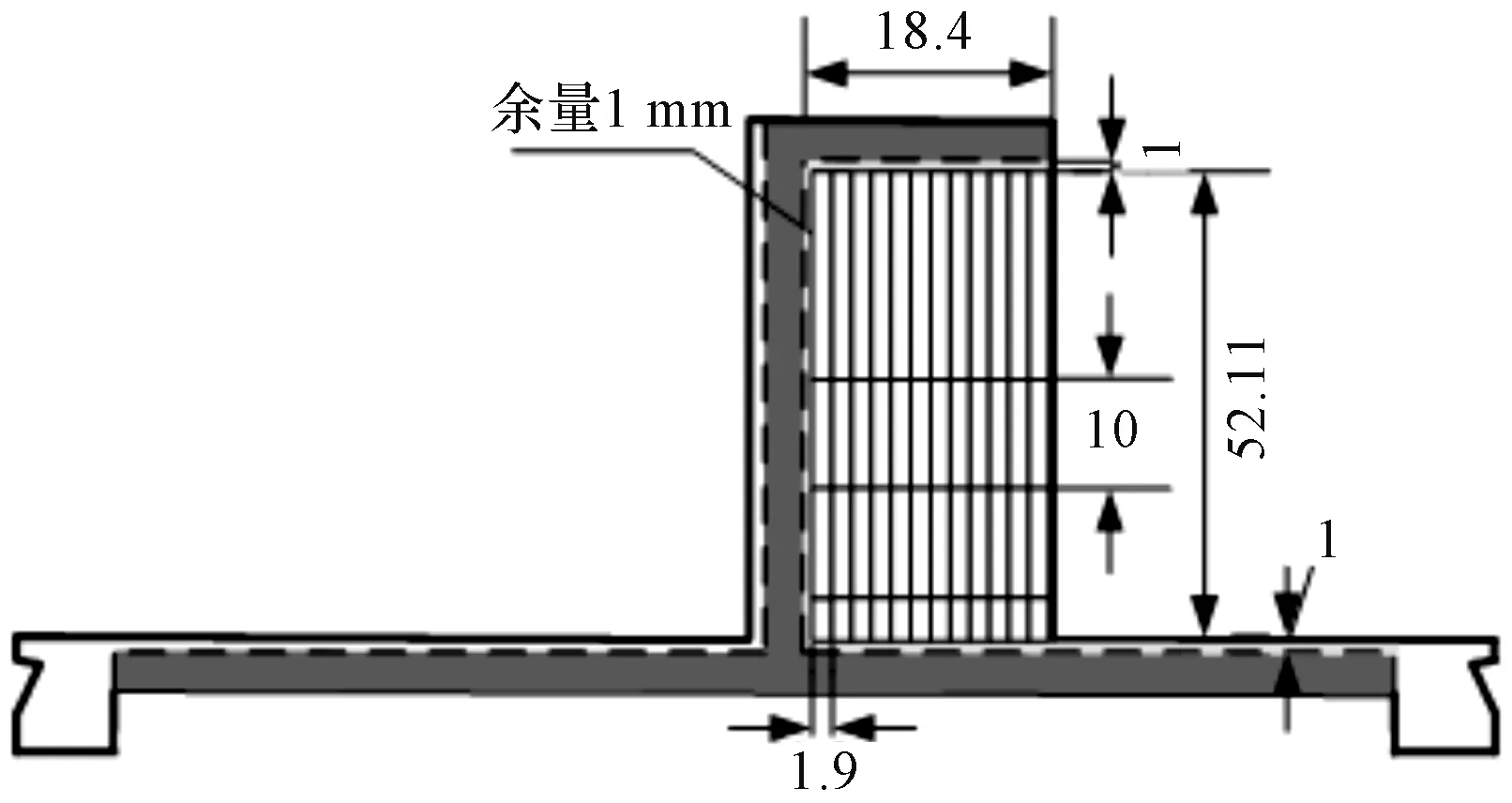
图6 粗铣缘板间余量优化后的工序简图

由图6可知,优选主轴转速n为16 000 r/min附近最大稳定域,优化切深ap为1.9 mm。

优化前后的铣削参数比较结果如表2所示。

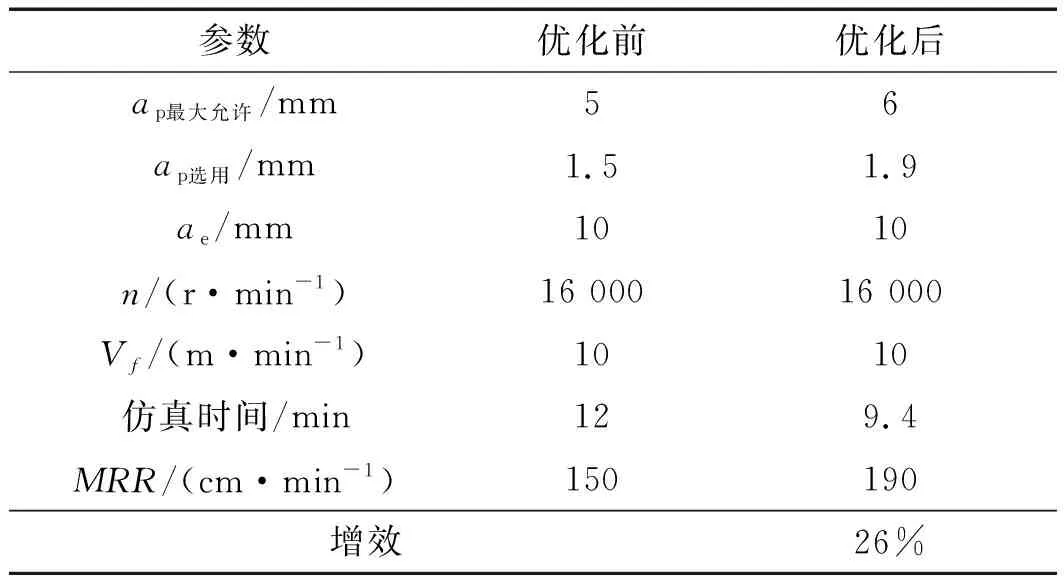
表2 优化前后参数对比

表2结果表明,经优化后该工步的切削效率提高了26%。

2 铣削参数优化模型

2.1 优化目标

加工表面选取材料去除率MRR和刀具寿命Ttool作为切削参数优化目标函数,可以在保证表面质量的前提下尽可能达到提高加工效率,延长刀具寿命的目的。

材料的去除率为:

MRR=ap·ae·ft·Z·n=1 000ap·ae·ft·Z·v(π·D)

(1)

式中:Z—铣刀齿数;ft—每齿进给量;n—主轴转速,r/min;D—铣刀直径,mm。

刀具寿命Ttool定以为刀具的平均更换时间,根据泰勒公式,刀具寿命可表示为[13]:

(2)

式中:Vc—切削速度;Ktool,σ1,σ2,σ3—正常数,通常采用统计方法确定。

此处优化的总体目标为效率、质量和成本,用材料去除率MRR表示效率,用刀具寿命表示成本,而用稳定性条件保证质量。

选择多目标线性加权求和法构建优化模型:

F(x)=ω1MRR+ω2Ttool

(3)

式中:ω1—最大金属切除率;ω2—刀具寿命的权重。

2.2 优化约束条件

优化目标函数需考虑约束条件的限制,主要与机床特性和加工特性有关,切削参数须在约束条件构建的约束域内进行变化。本研究考虑主轴功率和机床扭矩,对优化过程进行了约束。

2.2.1 主轴功率约束

铣削过程中,主轴实际消耗的瞬时切削功率Pt小于机床主轴电机的额定功率Pe。主轴功率约束条件可表示为:

(4)

式中:Pt—瞬时切削功率;Ft—主轴瞬时切向力;Pe—额定功率;ηs—机床加工效率。

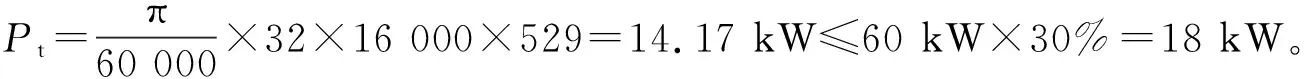
由此可知其满足主轴的功率约束条件。

2.2.2 机床扭矩约束

作用在主轴上的瞬时铣削扭矩Tc,可通过铣刀直径D与瞬时切向力Ft计算得到,主轴扭矩约束条件可表示为:

(5)

式中:Tt—机床能提供的扭矩。

根据上述预测铣削力的最大工艺参数,可求得其最大瞬时切削扭矩为:

由此可知其满足机床的扭矩约束条件。

2.3 优化方法

约束优化问题的数学模型归结如下:

(6)

由于目标函数是一个非线性方程,用传统的优化算法很难找到全局最优解,本文采用粒子群优化(particle swarm optimization,PSO)算法进行优化求解。

粒子群优化算法的基本过程如下:

假设在一个D维搜索空间中,由n个粒子组成一个种群X=(X1,X2,…,Xn),第i个粒子的位置可表示为Xi=(Xi1,Xi2,…,XiD)T。按照目标函数计算出每个粒子位置Xi对应的适应度值。第i个粒子的速度为可描述为Vi=(Vi1,Vi2,…,ViD)T,其个体极值为Pi=(Pi1,Pi2,…,PiD)T,种群的群体极值为Pg=(Pg1,Pg2,…,PgD)T。在迭代过程中,粒子可以通过个体极值和群体极值来更新自身的速度和位置,即:

(9)

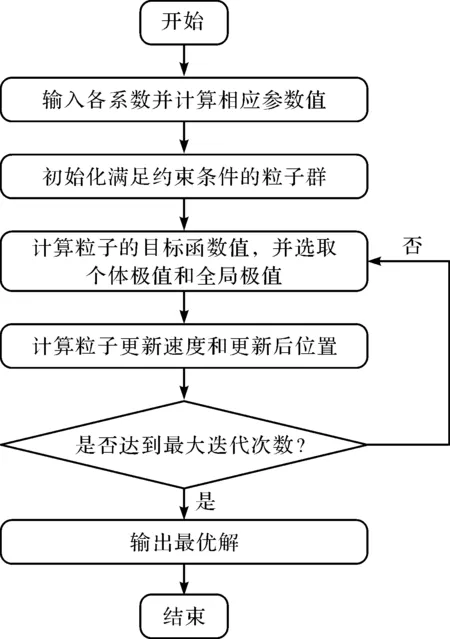
图7 粒子群优化铣削参数流程图

式中:ω—惯性权重,为常数;d—d维空间,d=1,2,…,D;i—第i个粒子数,i=1,2,…,n;k—当前迭代次数;Vid—粒子的速度;c1,c2—加速度因子,取c1=c2=2;r1,r2—服从均匀分布,分布于[0,1]区间的随机数。

粒子群算法的优化流程如图7所示。

工艺参数优化结果如表3所示。

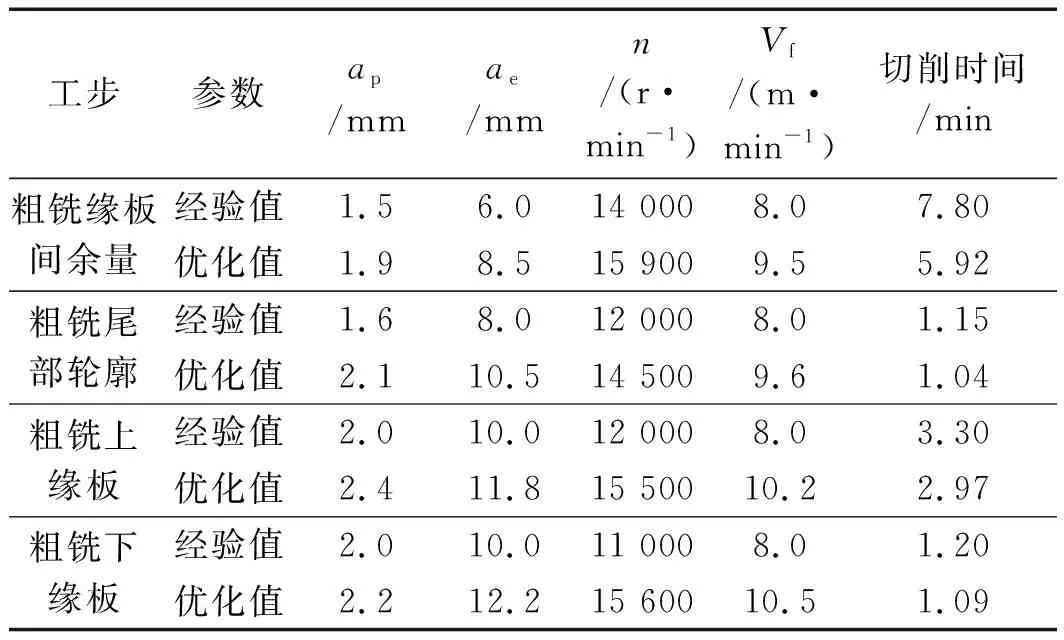
表3 工艺参数优化结果

切削时间主要取决于粗加工阶段时间。由表3可知,与数控机床企业提供的经验值对比,粗加工工步优化对应的切削时间更少。

3 长桁零件参数优化试验

3.1 铣削试验

笔者在五轴数控铣床上进行长桁零件的参数优化试验,试验现场如图8所示。

图8 长桁件铣削试验

该机床的最高转速为18 000 r/min,机床功率60 kW,扭矩60 N·m。

笔者采用表3中的工艺参数经优化组合,进行铣削实验,并利用测力仪记录铣削过程的切削力信号。粗、精加工选用同一型号直径为25 mm、2齿硬质合金铣刀完成,安装悬伸长度为70 mm。工件材料为铝合金。

由切削力系数辨识实验获得的切削力系数如表4所示。

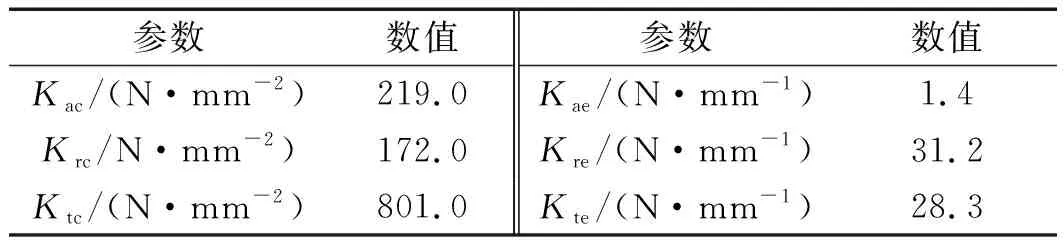
表4 切削力系数

3.2 工件—刀具系统锤击试验

笔者釆用模态锤击试验获取长桁铣削系统动态特性参数,亦即刀尖点频响函数和工件切削点频响函数,如图9所示。

图9 刀具—工件系统的频响测试

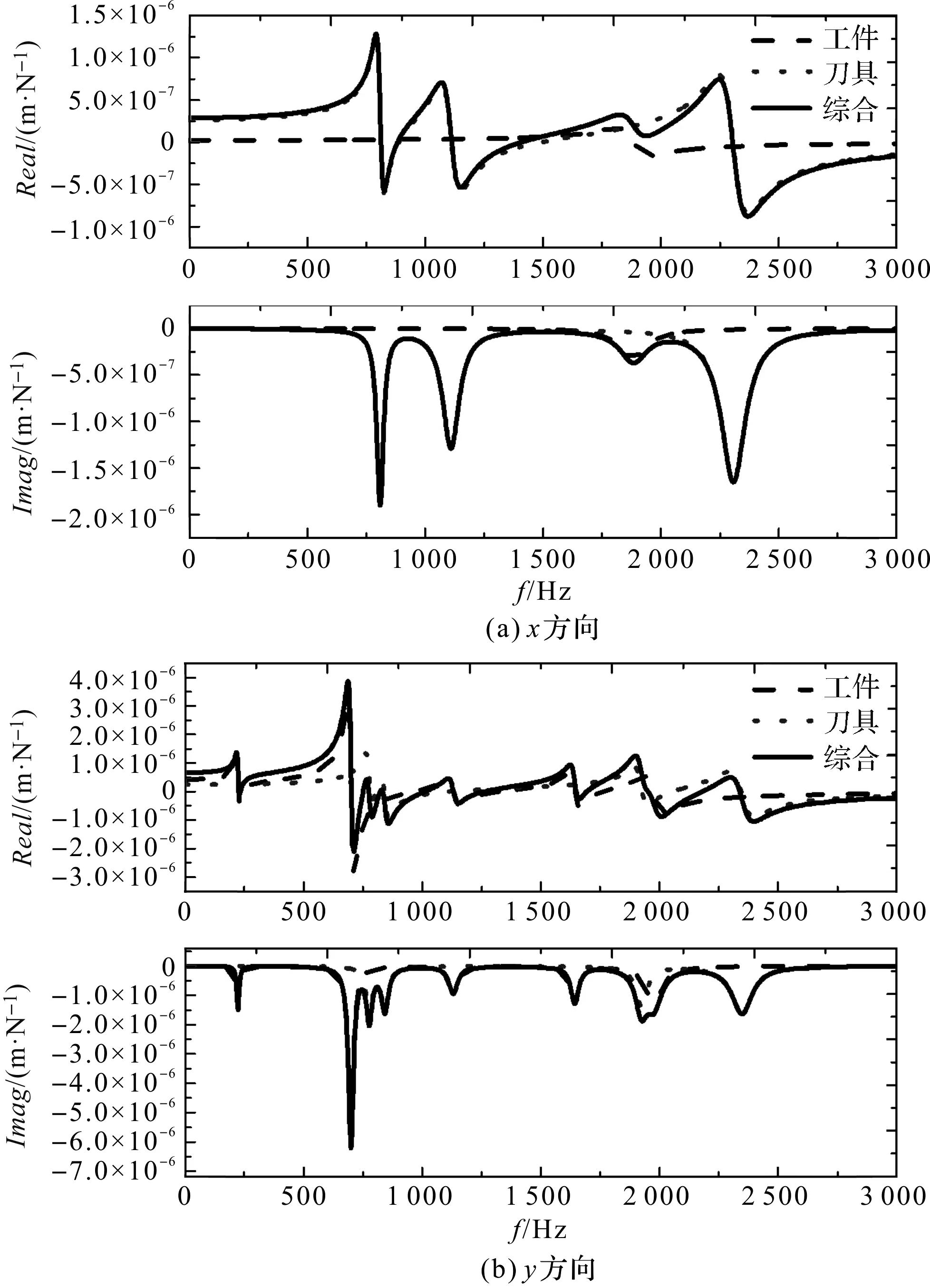
图10 刀具—工件系统实测频响函数及系统综合频响函数

图9中,笔者在铣刀刀尖处布置一个PCB加速度传感器(352C23),传感器采用蜂蜡粘结;在刀尖的另一端选用PCB力锤(M352C65)进行锤击,分为x和y方向,测振系统为LMS Test.Lab(SCM05);通过采集数据和系统分析,在计算机中显示出其频率响应函数曲线,各次均取10次有效锤击(相干系数大于0.8),统计平均值作为最后分析结果。

通过实验分别获取工件系统、刀具系统的频响函数后,笔者将两个子系统的频响函数进行运算,得到新的综合频响函数,如图10所示。

笔者根据试验识别的模态参数提取颤振主导模态的模态参数,如表5所示。

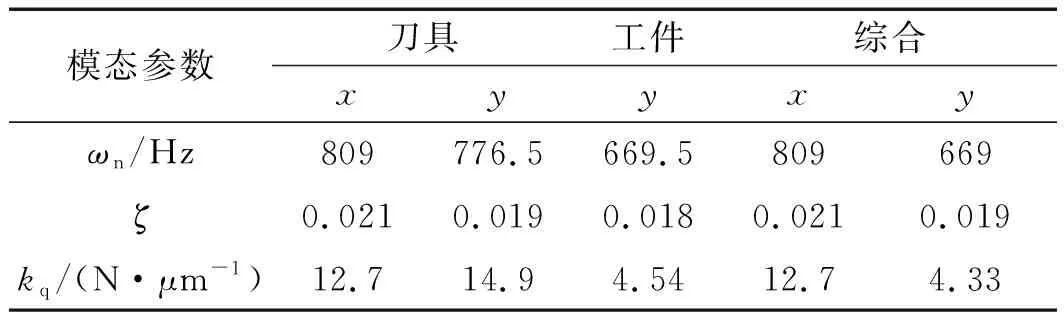
表5 刀具与工件主导模态参数

由表5可得,工件频响只有y方向的1个自由度,而刀具频响有x和y方向的2个自由度。

3.3 试验结果分析

长桁零件壁厚由4 mm铣削至3 mm时,笔者选择机床允许的、稳定区域较大的主轴转速进行变轴向切深试验,同时测试系统的振动信号;通过测得的振动信号频谱图,及对已加工表面是否出现振纹的观测,来判断该转速下铣削系统的稳定性轴向切削深度。

铣削参数优化前表面如图11所示。

图11 铣削参数优化前表面

在n=8 000 r/min切削条件下,得到的切削力信号与幅值频谱如图12所示。

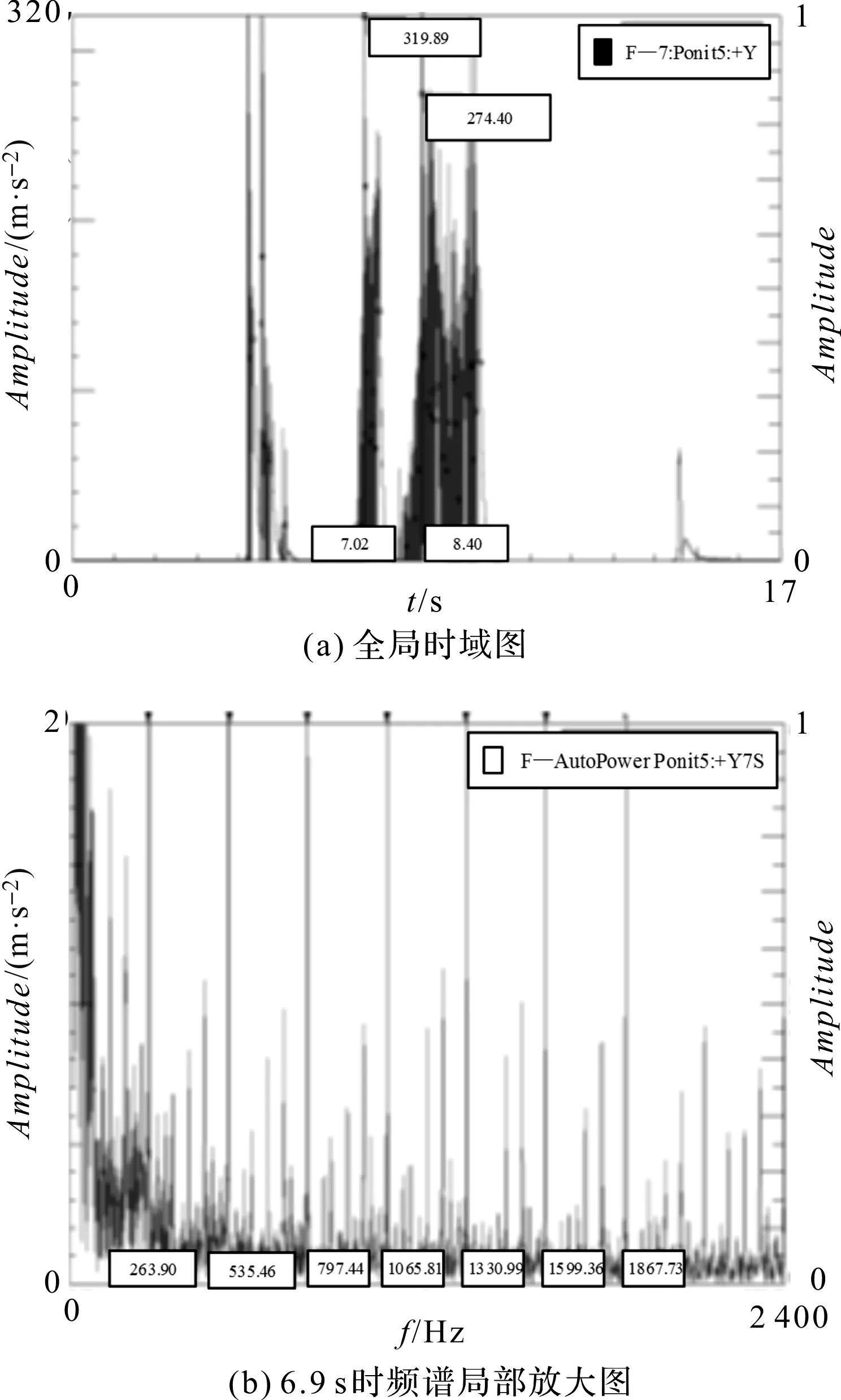
图12 n为8 000 r/min时的切削力信号与幅值频谱

由图12可知,n为8 000 r/min对应的刀齿通过频率为266 Hz,在齿频和齿频倍频的频谱线间出现了杂乱的频谱,判断是颤振点,该切削参数下实际加工表面有振纹出现。

而在n=16 500 r/min切削条件下,得到的切削力信号与幅值频谱如图13所示。

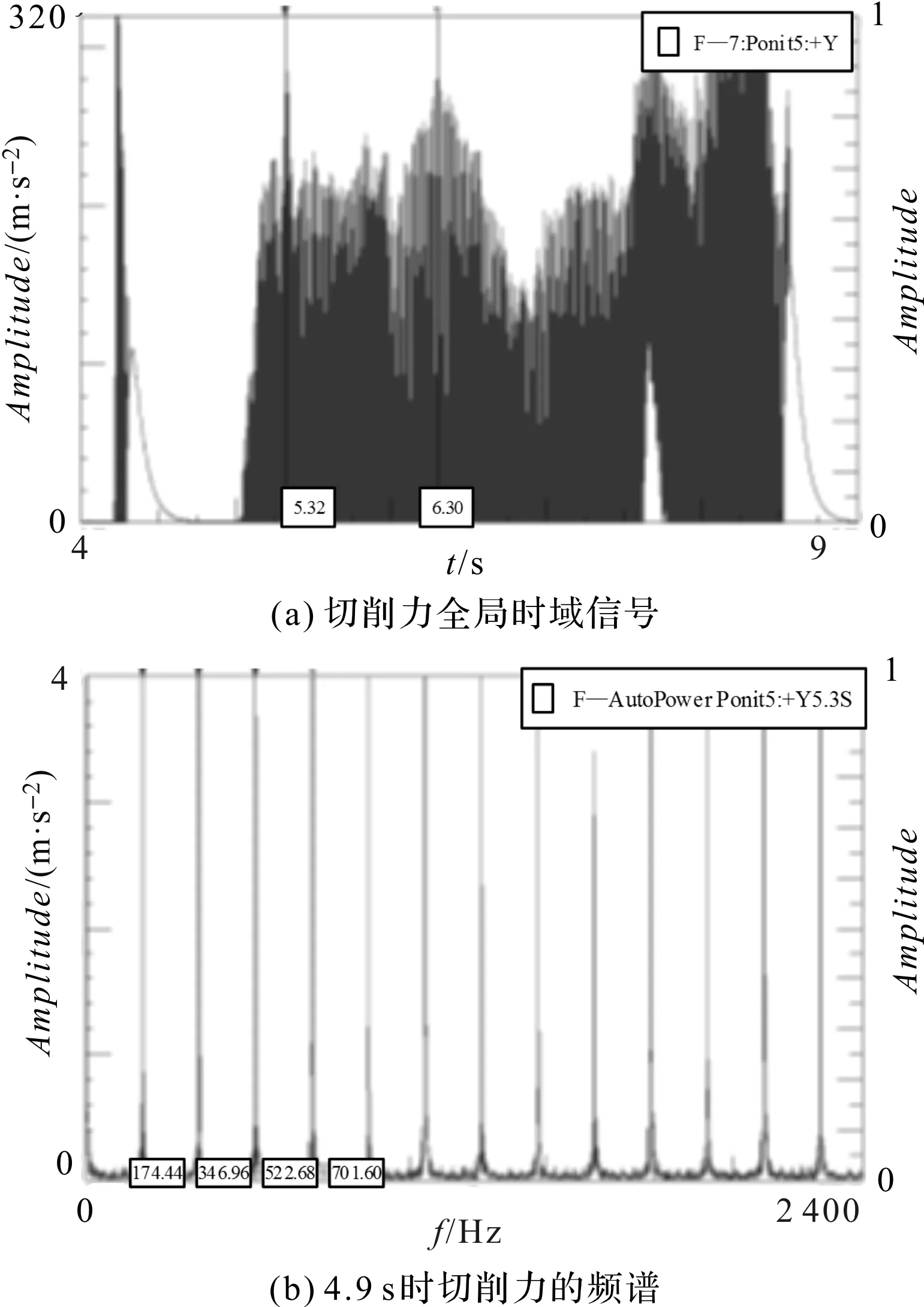
图13 n为16 500 r/min时的切削力信号与幅值频谱

由图13可知,n=16 500 r/min对应的刀齿通过频率为350 Hz,在齿频和齿频倍频的频谱线间没有出现杂乱的频谱,可以判断是稳定点,该切削参数下实际加工表面也是光滑的。

4 结束语

针对长桁零件铣削过程中的颤振会导致加工表面质量差、工艺参数偏保守,以及加工效率低等问题,笔者采用试验模态法和有限元模态法,进行了工件的系统动力学建模与稳定性分析;建立了综合考虑其他约束条件的切削参数优化模型,采用粒子群优化算法,实现了对长桁零件铣削无颤振和高效加工。具体结论为:

(1)获得了刀具系统和工件系统动力学特性参数,研究了典型长桁零件在不同加工阶段、不同加工位置的动力学特性变化规律;选取了长桁零件典型加工工步-粗铣缘板进行分析,建立了对应实际加工状态的铣削稳定域;

(2)建立了铣削参数优化模型,采用粒子群优化算法进行了主要加工环节的参数优化,对优化结果的对比表明了该优化算法的有效性;

(3)在长桁铣床上进行了切削力试验和锤击模态试验,获取了切削力模型和刀尖点频响,验证了优化参数组合的可靠性。

实验结果证明,在保证加工质量的前提下,长桁零件的加工效率得到了显著提高,经改进后,该型号长桁零件基本加工时间可缩短19%。该结果对同类长桁零件产品的加工具有指导意义和参考价值。

在后续的研究中,笔者将开展基于人工智能机器学习方法的航空结构件的制造参数优化研究。