机电系统一体化建模与动力学仿真向量键合图法*

王中双,师永珍,尹久政

(齐齐哈尔大学 机电工程学院,黑龙江 齐齐哈尔 161006)

0 引 言

随着现代机械装备性能的不断提高,系统不再局限于单一的机械能域,往往由多能域(例如机、电)子系统所构成。以分析力学及弹性力学为基础的各类动力学分析方法(例如牛顿-欧拉动力学方法、拉格朗日方法)及软件[1,2]仅适用于机械能域的系统,对于多能域系统的一体化计算机建模、动力学仿真及分析存在很大的局限性。

为解决上述问题,键合图方法[3]提供了颇具特色的有效途径,在实际工程中得到了广泛的应用[4-6]。文献[7]基于系统键合图的场和结型结构,较详细地阐述了用于计算机自动建立系统状态方程的矩阵法,该方法对于相当一部分机电系统是非常有效的。但在建立多体系统键合图模型时,每个键对应一个势变量和一个流变量,表达形式比较繁杂,实际应用非常不便。另外,多体系统键合图模型存在微分因果关系,也给实现计算机自动建模带来了非常大的代数困难。为此,文献[8]进一步扩展了键合图的概念,提出了向量键合图法。向量键合图的每个键对应一个势向量和一个流向量,表达方式简明,包含信息更大。文献[9,10]分别应用向量键合图法实现了电机驱动的平面开链机械臂系统、计及运动副间隙的平面四连杆机构的动力学分析,但由于其向量键合图存在微分因果关系,建立系统动力学方程的方式还都局限于手工推导。文献[11]将机构运动副约束反力向量视作未知势源向量,添加到系统向量键合图模型相应的0-结,可以完全消除微分因果关系,基于MLSD运动副间隙模型[12],应用向量键合图法实现了含运动副间隙的RRR-RRP六连杆压力机机构计算机建模与动力学仿真。

但是,对于有些非线性系统,其向量键合图贮能场和耗散场方程是非线性的,其建模方法具有很大的局限性。另外,由于MLSD模型采用线性弹簧阻尼描述间隙运动副的接触碰撞,实际应用中也具有局限性,例如不能反映碰撞过程中的能量转换特性,其弹簧阻尼器的参数难以确定等。

针对上述问题,笔者提出一种适用于计算机自动建模的向量键合图法,通过对计及驱动电机、非线性运动副间隙的曲柄滑块压力机机构系统进行一体化自动建模与动力学仿真,验证所述方法的可靠性及有效性。

1 系统状态方程及运动副约束反力方程

全积分因果关系系统键合图模型场和结型结构如图1所示。

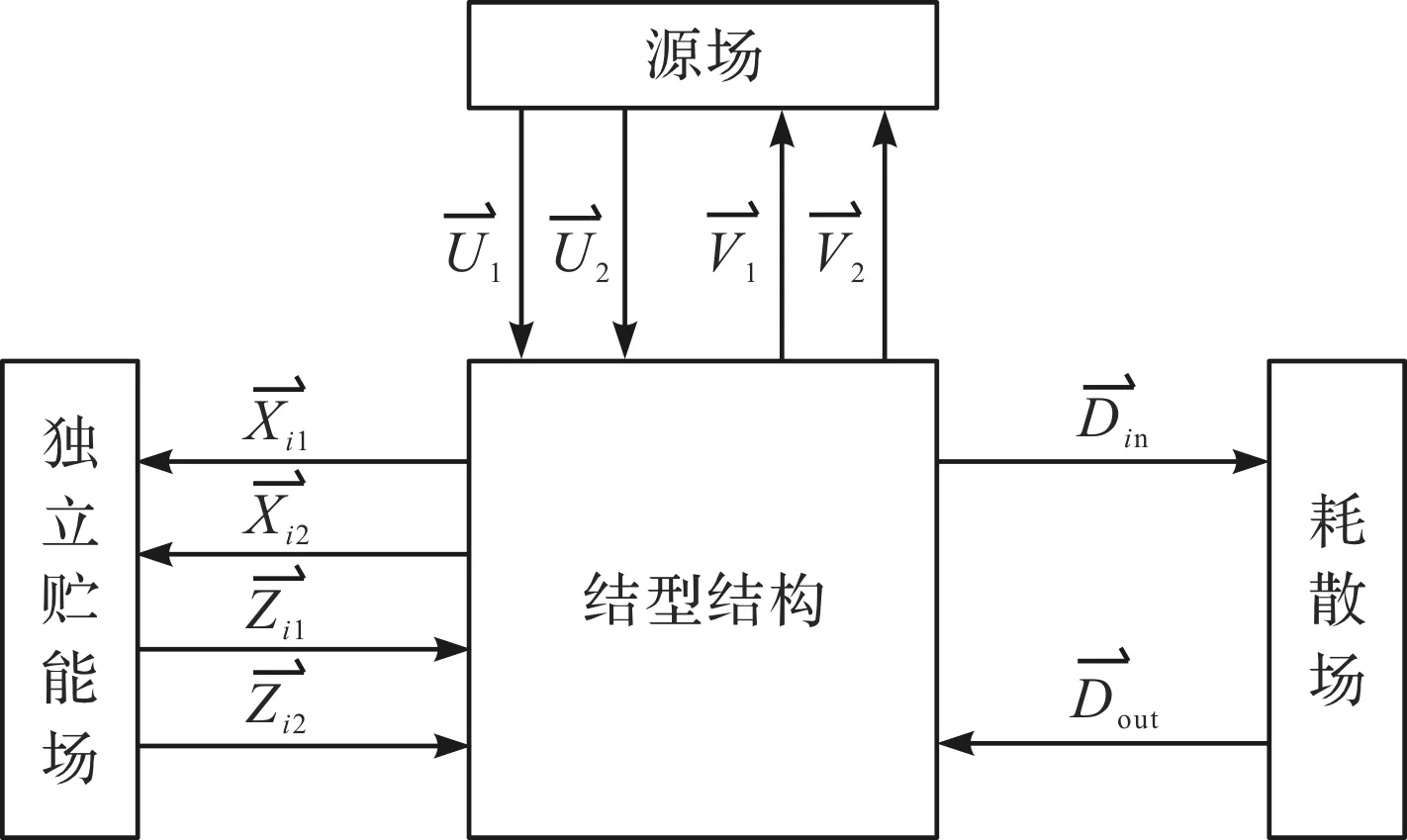
图1 全积分因果关系统键合图模型场和结型结构系统独立贮能场独立运动的能量变量向量,为m1维列向量;系统独立贮能场非独立运动的能量变量向量,为m2维列向量;系统独立贮能场独立运动的共能量变量向量,为m1维列向量;系统独立贮能场非独立运动的共能量变量向量,为m2维列向量;耗散场的输入向量、输出向量,为L维列向量;系统已知源输入向量,为ms维列向量;系统运动副约束反力向量,为mu维列向量

由图1可知,对于系统独立贮能场,可将其特性方程列写成如下非线性的形式:

(1)

(2)

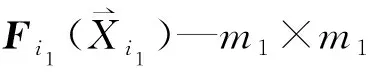
对于系统耗散场,可将其特性方程列写成如下非线性的形式:

(3)

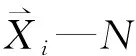
系统的结型结构方程可写成如下形式[13]:

(4)

(5)

(6)

(7)

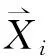
将式(1～7)联立,经进一步代数处理可建立系统状态方程及运动副约束反力方程。

当det(TLE)≠0时,有:

(8)

式中:I1—L×L单位矩阵。

当JCL=0时,有:

(9)

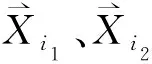
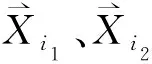
2 计及运动副间隙的机电系统向量键合图模型

电机驱动含间隙曲柄滑块压力机机构系统如图2所示。

由图2可知,曲柄AB质心位于A点,其余各杆件均匀。

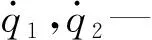
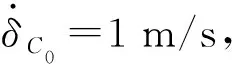
驱动电机参数如下:电枢线圈电感、电阻分别为La=0.05 H,ra=0.4 Ω,换能系数T=0.678 N·m/A,转子阻尼系数Da=0.226 N·m·s/rad,电机输入电压Vt=60 V,电枢线圈电流强度ia,其初始值ia(0)=0。

系统向量键合图模型如图3所示。

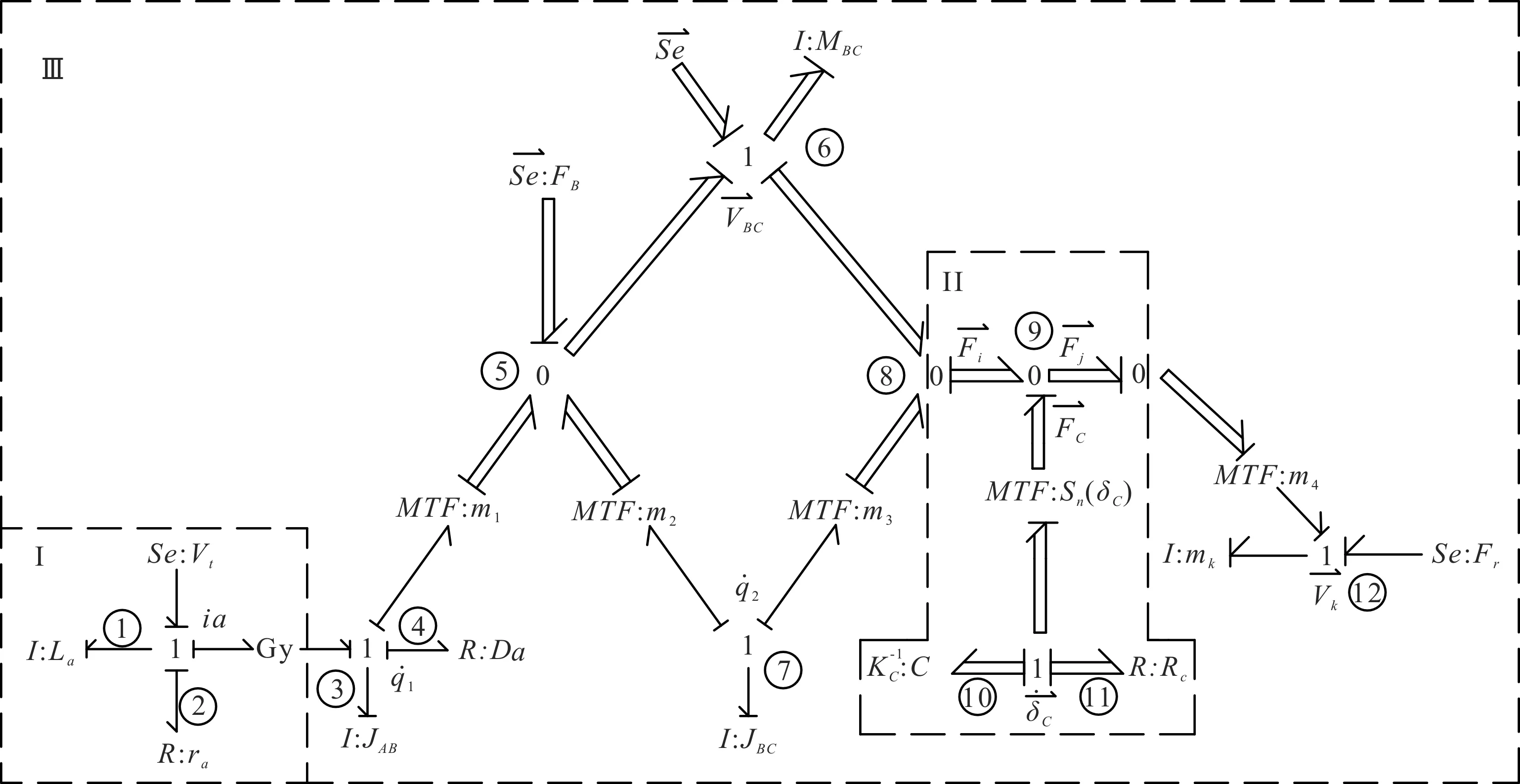
图3 系统向量键合图模型滑块(刀具)的速度向量;容性元件C10的广义位移、广义速度向量,即轴与轴套相互碰撞的压入深度向量、相对弹性变形速度向量;δC—轴与轴套相互碰撞的压入深度;MBC—连杆BC的质量矩阵,连杆BC质心速度向量,

该系统永磁式直流驱动电动机的键合图模型如图3中的Ⅰ部分所示[16]。该机构曲柄AB、连杆BC彼此间用转动副连接,滑块(刀具)与机架通过移动副连接。由于机构运行时滑块(刀具)冲切工件会发生碰撞与冲击,连接连杆BC与滑块(刀具)的转动副C受实际冲切力的影响最直接,极易产生磨损,故这里仅计及转动副C的间隙。笔者分别建立图2所示机构各构件的向量键合图模型,将其按照机构的上述运动约束关系键接起来,可以建立计及运动副间隙的曲柄滑块压力机机构向量键合图模型,将其与图3Ⅰ驱动电机的键合图模型进一步键接,可以建立图2所示机电系统完整的向量键合图模型。其中,间隙转动副C的向量键合图模型如图3中的Ⅱ部分所示。

转动副C间隙模型简图如图4所示。

图4 转动副C间隙模型简图Ri—轴套的半径;Rj—轴的半径;旋转铰C轴与轴套的偏心向量;e—旋转铰C轴与轴套的偏心量

由图4可知:间隙转动副C用修正非线性连续接触碰撞力混合模型来描述。该模型是在L-N碰撞力模型[17]及改进弹性基础模型[18]的基础上提出的,解决了碰撞刚度系数的取值问题,且不受间隙尺寸和恢复系数的限制,实际应用中能够更精确地描述运动副间隙。构件i表示轴套,构件j表示轴,Oi、Oj分别为轴套和轴的轴心点。

设轴与轴套的半径差为c,则有:

δC=e-c

(10)

c=Ri-Rj

(11)

为建立间隙转动副C的向量键合图模型,笔者将间隙转动副碰撞力进一步归纳整理成向量形式:

(12)

(13)

(14)

(15)

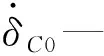
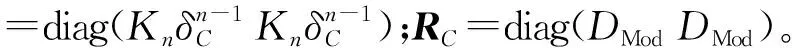
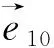
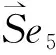
3 系统动力学仿真及分析

由本文所述方法可得图3中与图1相对应的向量,其中:

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

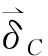
由图3所示系统向量键合图,可以建立方程(1～3)的函数关系矩阵:

(24)

(25)

同时,也可以确定方程(4～7)中的函数系数矩阵。

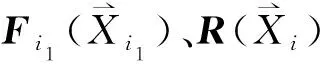
无间隙机构、有间隙机构运动副C约束反力合力曲线、滑块(刀具)加速度曲线、运动副B约束反力合力曲线如图5所示。

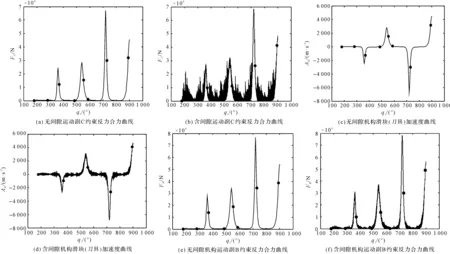
图5 机构动力学仿真实验结果曲线

为验证上述仿真结果的可靠性,笔者应用牛顿-欧拉动力学方法及电工学方法,分别建立该系统机械部分及驱动电机的动力学方程,并联立求解。

无间隙机构牛顿-欧拉动力学方法验证的部分结果如表1所示。

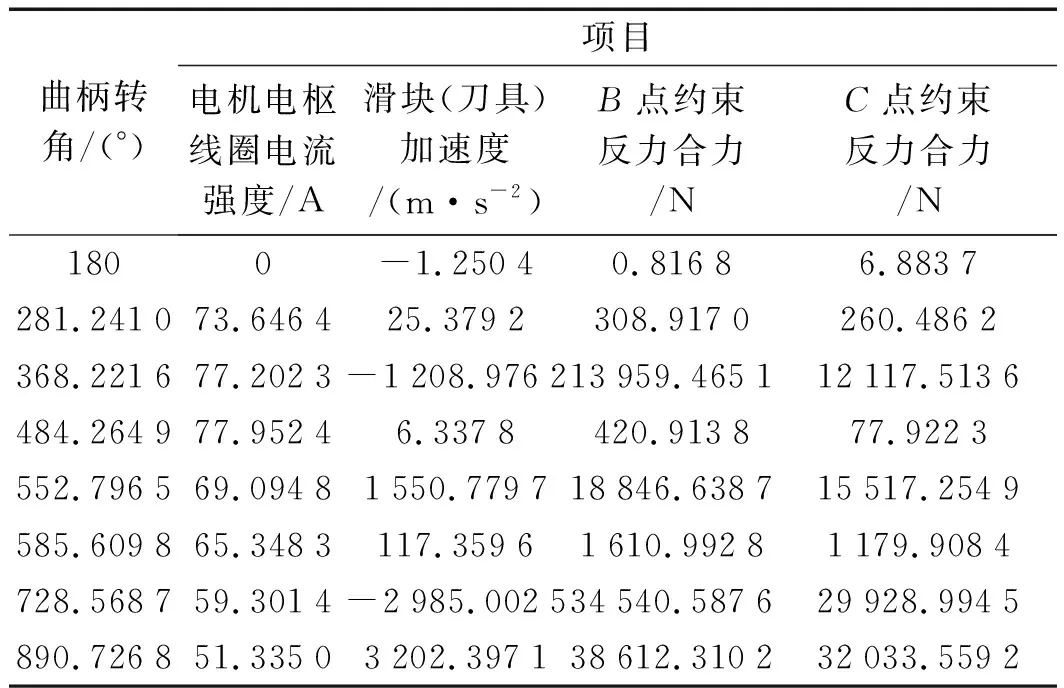
表1 无间隙机构牛顿-欧拉动力学方法验证的部分结果

含间隙机构牛顿-欧拉动力学方法验证的部分结果如表2所示。

表2 有间隙机构牛顿-欧拉动力学方法验证的部分结果

由表1、表2可知:牛顿-欧拉动力学方法验证的部分结果与用本文方法所得结果是一致的。为更加清晰、直观地表达这一点,将表1、表2所列数据用涂黑的圆点表示在图5中,结果显示这些圆点均在相对应的仿真曲线上。这一验证过程手工处理量较大,比较费时且容易出错。

由此可见,本文方法具有如下明显的优势:(1)将机电耦合系统的动力学建模以统一的程式化方式由计算机来完成,提高了系统动力学建模与仿真工作的自动化程度及可靠性;(2)与现有的键合图方法相比较,本文所推出的系统状态方程更具有通用性,特别适用于Fi1、Fi2、R为状态变量函数矩阵的非线性系统。

由图5可知：曲柄的初始位置角为180°;曲柄由初始位置逆时针转720°,机构完成2个周期的运动。

由图5(a,b)可得:在系统运行过程中,对于有间隙及无间隙的运动副C,其约束反力曲线总体变化趋势相近。不考虑间隙时,运动副C的约束反力曲线较光滑。运动副间隙导致其轴与轴套间产生脉冲式的间隙碰撞力,使有间隙的运动副C约束反力曲线呈高频振荡状态,其最大幅值明显增大。角位移q1=719.983 5°时,无间隙运动副C约束反力的最大值为67 064.328 4 N;角位移q1=719.242 9 °时,有间隙运动副C约束反力的最大值为69 446.965 7 N,其最大值增加了2 382.637 3 N。两者达到最大值的曲柄角位移差为0.740 6°,这表明运动副C约束反力对其本身的间隙十分敏感。另外,在图5所示的两个运动周期内,间隙运动副约束反力合力FC始终大于0,表明运动副轴与轴套处于连续接触状态。

由图5(c,d)可得：不考虑运动副间隙时,机构滑块(刀具)加速度曲线较光滑。考虑运动副C的间隙时,由于间隙对其约束反力的影响,使机构滑块(刀具)加速度曲线呈高频波动状态。与无间隙机构相对比,有间隙机构刀具的加速度曲线变化趋势相近,但其正、反向最大幅值均明显增大。角位移q1=719.983 5°,无间隙机构滑块(刀具)加速度的反向最大值为-6 706.429 9 m·s-2;角位移q1=719.242 9°,含间隙机构滑块(刀具)加速度的反向最大值为-6 925.966 6 m·s-2,其反向最大值的绝对值增加了219.536 7 m·s-2,两者达到反向最大值的曲柄角位移差为0.740 6°;当角位移q1=900°时,无间隙机构滑块(刀具)加速度的正向最大值为4 584.939 9 m·s-2,含间隙机构滑块(刀具)加速度的正向最大值为4 848.041 2 m·s-2,其正向最大值增加了263.101 3 m·s-2,这会在较大程度上影响机构运动的稳定性。

由图5(e,f)可得:无间隙机构运动副B约束反力曲线较光滑。由于间隙对运动副C约束反力的直接影响,也使得机构运动副B约束反力曲线呈高频波动状态。与无间隙机构相对比,有间隙机构运动副B约束反力曲线变化趋势相近,但其最大幅值明显增大。角位移q1=719.983 5°时,无间隙机构运动副B约束反力的最大值为76 909.736 4 N,角位移q1=719.242 9°时,有间隙机构运动副B约束反力的最大值为79 068.454 6 N,其最大值增加了2 158.718 2 N,两者达到最大值的曲柄角位移差为0.740 6°,这表明运动副B约束反力对运动副C的间隙也比较敏感。

由此可见,运动副间隙导致其轴与轴套间产生脉冲式的间隙碰撞力,使机构运动副C的约束反力、刀具加速度及运动副B的约束反力的最大值分别增加了3.55%、5.7%、2.8%。这会使机构运行产生较大的冲击、振动及噪声,影响机构运动的稳定性,也会降低机构构件的强度及使用寿命。

4 结束语

(1)在系统贮能场、耗散场方程是非线性的条件下,笔者建立了系统状态方程及运动副约束反力方程,比现有同类方法通用性更强,适用范围更广,其程式化的建模方式特别适用于复杂非线性机电系统一体化计算机建模与动力学仿真;

(2)基于修正非线性连续接触碰撞力混合模型,笔者推导出了间隙运动副接触碰撞力向量方程。在此基础上所建立的间隙转动副向量键合图模型,具有精细度高、模块化的特点,便于嵌入到系统的向量键合图模型中,为更精确计及运动副间隙的机电系统一体化计算机建模及动力学仿真奠定了基础;

(3)根据所建立的计及驱动电机、运动副间隙的曲柄滑块压力机机构系统向量键合图模型,实现了系统的一体化计算机建模及动力学仿真。

研究结果表明:本文所述方法是可靠的,提高了机电系统动力学建模与仿真工作的自动化程度;运动副C的间隙对系统动态性能产生一定程度的影响,使机构运动副C的约束反力、刀具加速度及运动副B的约束反力呈高频振荡状态,其最大值分别增加了3.55%、5.7%、2.8%。该结果说明了本文方法的有效性,对于机构的设计、控制及可靠性问题的研究具有一定的价值。