基于GPS 时间序列分析的地震前后噪声特性差异性研究

(中国铁路设计集团有限公司，天津 300142)

0 引言

地震的很大一部分能量在震前会以各种形式缓慢释放，从而形成各种前兆.传统的地震前兆监测方法为地下水、地磁、重力、地温、地应力等，这些监测方法具有自动化程度低、不能全天候连续监测等缺点，而全球卫星导航系统(GNSS)却能很好地弥补这些不足.随着空间大地测量技术的不断发展，GNSS在地震前兆监测中的作用越来越大.

当前，国内外学者对GPS 时间序列及对地震的响应进行了研究.如Alexey Lyubushin 等[1]研究了日本1 203 个测站在日本东北大地震前后的谱指数分布，指出即将发生地震的区域相对其他区域具有较大的谱指数，并得出GPS 可以用来预测地震的结论；张燕等[2]对昆仑山8.1 级地震和美国西雅图7.0 级地震进行了研究，指出在地震前1～2 a 或稍长的时间开始，站点运动态势会发生改变，并在地震后恢复常态；敬少群等[3]就时间序列对昆仑山口西8.1 级地震的响应进行了分析，指出GPS 时间序列对地震的孕育过程反映明显；范士杰等[4]利用地震前后共7 天的GPS 观测数据对日本里氏9.0 级特大地震的震时、震后地表震动信息进行了研究，认为较近站点均能完整记录主震波引起的地表位移过程.由于现有地震预测研究中噪声特性分析方面的研究较少，因此分析较大地震对GPS 时间序列噪声特性的影响进行分析极为必要.

本文的主要目的在于利用不同跨度的GPS 时间序列(5 个时段)，采用多种类型的噪声模型组合分析地震临近测站GPS 坐标时间序列的随机特性，并对地震前后各时段内求取的谱指数、噪声分量、速度场等进行对比分析，研究较大地震对GPS 坐标时间序列噪声特性的影响，并得出结论.

1 GPS 数据介绍及数据分析

1.1 数据介绍

选择近20 年来的较大地震及相应临近测站，为保证研究的正确性，在选择测站时，需考虑所选测站在研究时段内是否受其他较大地震的影响.测站坐标时间序列选用斯克里普斯轨道和永久阵列中心(SOPAC)提供的8 个IGS (国际GNSS服务)基准站坐标时间序列数据.Blewitt 等[5]的研究表明，若测站坐标时间序列跨度短于2.5 a，测站速率受季节性信号影响很大.由于本文所用时间序列跨度较短，为避免测站速度等受到季节性信号的影响，选择同一季节时段的GPS 坐标时间序列对地震前兆反应进行分析，所选时间序列为震前4～3 a、前3～2 a、前1～0 a、震后0～1 a、后1～2 a 五个时段.较大地震及相应临近测站信息如表1 所示，时间序列分段概况如表2 所示.

表1 较大地震及相应测站信息

表2 GPS 时间序列分段概况

1.2 数据处理策略

对GPS 坐标时间序列进行噪声分析的方法通常有功率谱分析和最大似然估计(MLE)两种，分别从频率域和时间域对时间序列中存在的噪声进行分析，确定GPS 坐标时间序列中包含的噪声的性质和强度.其中，MLE 可以同时估计噪声类型、周期性振幅、测站速度等，并可以避开频谱分析要求数据均匀采样、依赖于频谱平均的局限性，被认为是目前最准确的噪声分析方法.本文选取WN、FN+WN、RWN+WN、FN+RWN+WN、PL+WN、FOGM+WN、FOGM+RWN+WN 共七个噪声模型(注：WN 为白噪声、FN 为闪烁噪声、RWN 为随机漫步噪声、PL 为功率谱噪声、FOGM 为一阶高斯马尔科夫噪声)，采用CATS 软件对IGS 基准站各时段进行噪声分析[6].

1.3 最优噪声模型评价准则

根据MLE 原理，噪声模型得到的MLE 对数值越大，结果越可靠，但其数值也受到噪声模型中未知参数的影响，未知参数越多MLE 值越大，如表3 所示.因此本文选用Langbein 提出的保守准则判断不同模型的优劣，先以WN 零假设，然后将FN+WN 及RWN+WN 模型的MLE 值与零假设作比较，如果MLE 差值大于2.6 则拒绝零假设，否则认为所选模型无效.若两种模型均优于零假设，则选择MLE 值较大者作为“最优”模型.假设此时FN+WN 为最优模型，则接受PL+WN 的阀值为2.6，接受FOGM+RWN+WN 的阀值为5.2[7].

表3 各噪声模型未知参数个数统计

2 GPS 坐标时间序列最佳噪声模型的建立

2.1 谱指数的求取

GPS 坐标时间序列的功率谱(power spectral)谱指数为双对数空间中功率谱拟合直线的斜率.谱指数计算是一种有效进行噪声特性分析的方法，本文利用CATS 软件求取每个测站在地震前后各时段内的谱指数，如表4 所示(限于篇幅，仅列出4 个测站的谱指数，其他表格也是如此).

将地震前后每个时段的谱指数与震前1～0 年的谱指数进行对比，并对结果进行统计分析，结果表明：单个时段(即震前4～3 a、前3～2 a、震后0～1 a、后1～2 a)相对于震前1～0 a 谱指数变化无明显规律；震前4～3 a、前3～2 a 相对于震前1～0 a 谱指数具有相同变化趋势(即同大或同小)的比例为66.67%；震后0～1 a、后1～2 a 相对于震前1～0 a 谱指数具有相同变化趋势的比例为70.00%；地震前后谱指数相对于震前1～0 a 具有一定的一致性，与地震时能量释放，震后站点运动态势恢复常态相一致.

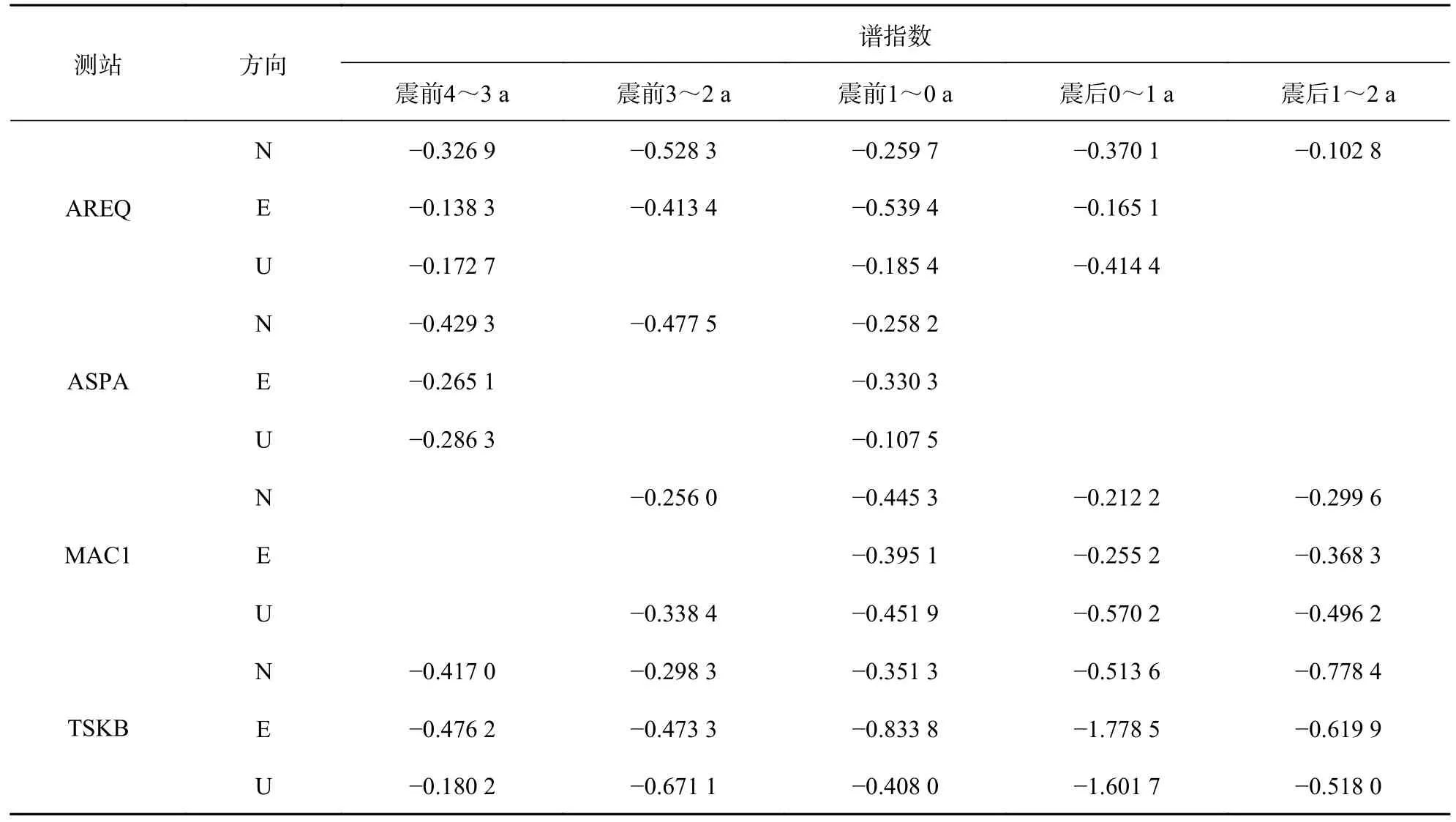
表4 4 个测站的谱指数

2.2 最优噪声模型的建立

采用1.2 节的数据处理策略和1.3 节的最优噪声模型评价准则，对选取的8 个IGS 基准站各时段按照上述7 种噪声模型组合进行噪声特性分析，可得到各测站在地震前后的最优噪声模型，结果如表5 所示.

对8 个IGS 基准站在各时段内的最优噪声模型进行统计，结果发现WN、FN+WN 所占比例较大，且变化规律明显，如图1、图2 所示，仅列出这两种模型在各时段内的变化趋势.

由图1、2 可知，地震孕育期间，WN 在所有最优噪声模型中所占比例下降，FN+WN 所占比例上升，且在震后有所恢复.其余最优噪声模型在各时段内无明显规律，未显示.

2.3 FN+RWN+WN 噪声分量的求取

对FN+RWN+WN 中各噪声分量在每个时段中所占比值进行了统计，如图3 所示.

由图3 可知，地震孕育阶段，WN 所占比例下降，FN 比例上升，震后均有所恢复，与地震时能量释放，震后站点运动态势恢复常态相一致.由于时间序列跨度较短，且因FN 等的掩盖，每个测站在各时段基本未显现出RWN.

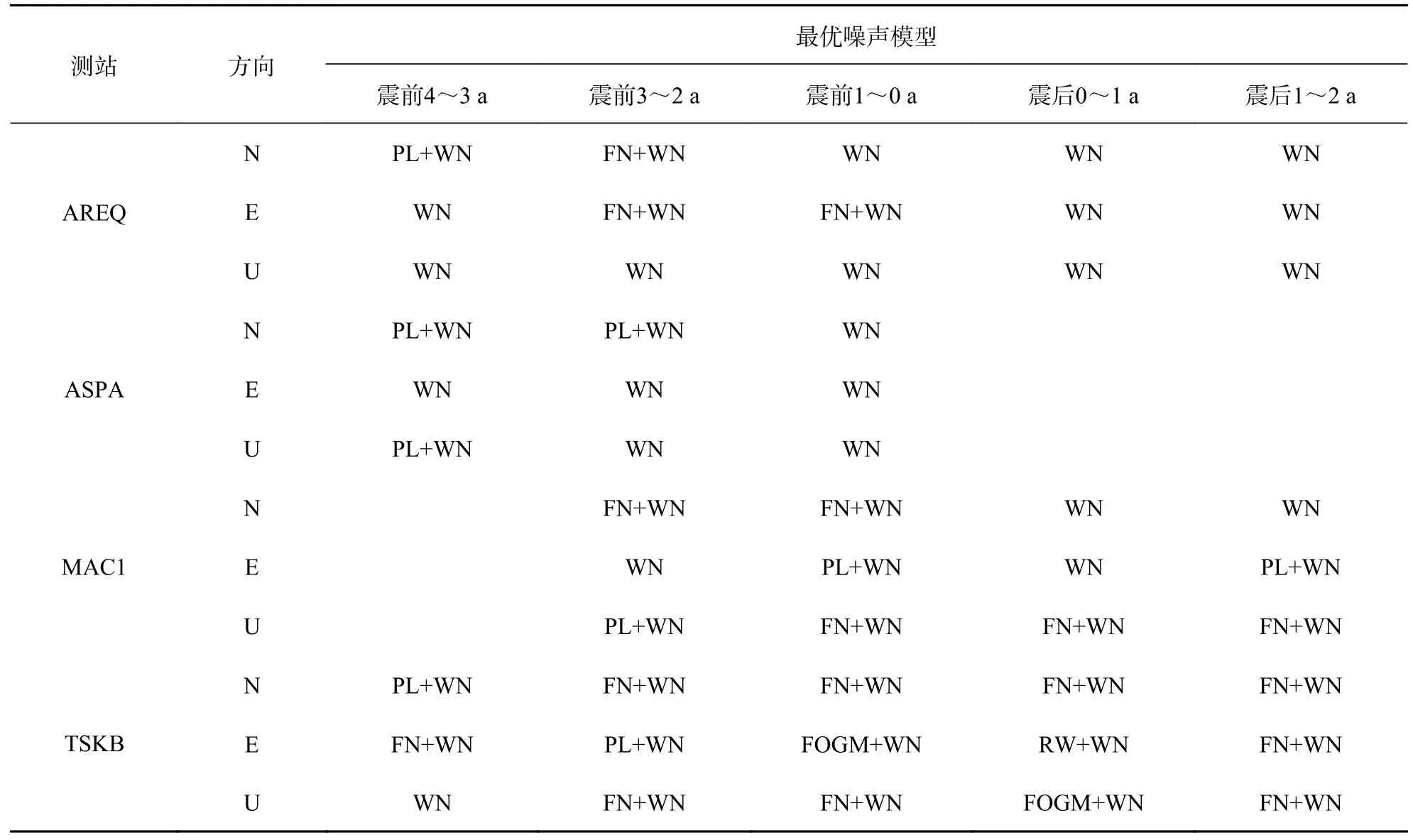
表5 4 个测站的最优噪声模型

图1 WN 在各时段内所占比例

2.4 速度场的求取

根据最优噪声模型可提取相应的速度场，并对各时段速度场进行统计，如表6 所示.

图3 各噪声分量在每个时段中所占比例

对每个测站在各时段内的速度场进行统计分析，可知：除个别测站外，地震前后站点速度场均会产生较大变化；AREQ、ASPA、MAC1、TSKB 等测站地震前后速度场较震前1～0 a 速度场具有一致性.

2.5 振幅、相位在地震前后各时段的变化

根据最优噪声模型可提取相应测站年周期和半年周期的系数，按照公式振幅，相位求取时间序列的振幅和相位.各时段内的周年振幅、相位如表7、表8 所示.

对每个IGS 基准站在地震前后各时段的周年振幅、相位进行统计分析，可知：地震前后振幅变化较大；AREQ、ASPA、MAC1、TSKB 等多个测站地震前后周年振幅较震前1～0 a 周年振幅具有一致性；地震前后周年相位变化较大，但无明显规律.

表6 4 个测站各时段分量速度场

表7 4 个测站的周年振幅

3 结束语

利用GPS 监测地震孕育及发生的过程是近年来的研究方向之一[8-10].本文通过对8 个IGS 基准站在地震不同阶段的GPS 坐标时间序列进行噪声特性分析，得出以下结论：地震前后谱指数、速度场、振幅相位等变化较大，GPS 坐标时间序列噪声特性对地震响应明显；部分测站地震前后谱指数、速度场、周年振幅等较震前1～0 a 具有一致性；地震孕育阶段，FN+WN 在所有最优噪声模型中所占比例上升，FN+RWN+WN 中FN 在所有噪声分量中所占比例上升，且在震后均下降，而WN 与其相反，这些均与地震时能量释放，地震后站点运动态势恢复常态相一致.

表8 4 个测站的周年相位

随着GNSS 技术的快速发展，采用更高时间频率的GPS 坐标时间序列资料进行噪声特性分析可能会给地震预测研究带来意外的收获，是今后的研究方向.