载人月球极地探测地月转移轨道设计
陆 林,李海阳,周晚萌,刘将辉
(1.国防科技大学空天科学学院,长沙 410073;2. 空天任务智能规划与仿真湖南省重点实验室,长沙 410073;3. 中国航天员科研训练中心,北京 100094;4. 中国人民解放军91395部队,北京 102443)
0 引 言
在各国致力于载人深空探测的时代浪潮中,世界上的主要航天国家都将月球作为下一步探索的对象[1-3]。早期美国Apollo任务的月球探测着陆区主要集中在赤道附近,但由于月球极地的特殊位置环境,加上水冰的发现[4-5],使得月球极地具有不可替代的科学探索和应用开发价值。因此,人类对月球极地地区的关注度不断增加,并将其作为下一步月球探测的热点区域[6-7],乃至考虑未来在月球极地建立基地。但是载人月球极地探测是一项庞大的系统工程,轨道方案是其中的重要组成部分,轨道的设计与特性分析对于任务具有重要意义。
关于地月转移轨道方案的设计与分析,目前有很多学者做了研究。文献[8]结合圆锥曲线拼接法,提出一种着陆器三层奔月窗口搜索方法,并求解了奔月轨道。文献[9]对基于地月平动点的月球探测轨道研究进行了概括总结。文献[10]提出一种近月点伪经度判别准则,并采用多圆锥截线法快速求解地月转移轨道。而在实施载人月球极地探测任务的过程中,保障航天员的生命安全是在选择轨道方案时需要考虑的重要因素。但上述地月转移轨道方案耗时较长,在长时间的飞行中,航天员的生命安全难以得到保证,所以上述方案更加适合无人探月任务。而针对载人登月任务的地月转移轨道设计,目前的研究也取得了一些进展[11-12],其中传统的绕月自由返回轨道能够有效保证航天员在地月转移阶段的安全返回[13]。文献[14]研究了返回高纬度着陆场的非对称绕月自由返回轨道。文献[15]提出一种混合-分层轨道优化设计方法对自由返回轨道进行了设计。文献[16]提出一种基于UKF参数估计算法的绕月自由返回轨道设计方法,可以快速得到高精度模型下的收敛解。文献[17]采用混合多圆锥截线法对自由返回轨道进行设计,并分析了轨道相关特性。文献[18]结合圆锥曲线拼接法,对四类自由返回轨道的解集域进行了分析。但此类轨道月面可达域的分布范围较小,主要集中在中低纬度地区[19]。因此,若要实现对月球极地地区的探测,同时保证轨道的安全性,需要在自由返回轨道基础上进行可达域的扩展,通常有混合轨道和三脉冲机动轨道两种方案[20]。其中,三脉冲机动轨道方案是指在近月点处开始实施轨道机动,从而能够到达更大倾角的环月轨道,并且在奔月过程中均可以实现无动力返回,安全性较高。文献[21]基于双二体假设,对混合轨道的能量消耗和飞行时间等方面的特性进行了分析。文献[22]详细介绍了混合轨道和三脉冲机动轨道,并简单地分析了速度增量特性。文献[23]研究了不同的三脉冲机动轨道方案,并给出了不同方案消耗的速度增量大小。文献[24]采用二体解析模型分析了三脉冲机动方案的相关特性。此外,采用两段自由返回轨道的方案也可实现全月面到达[25]。文献[26]利用伪状态理论对两段绕月自由返回轨道进行了设计,并分别采用梯度与直接打靶法对两段轨道的初值进行了修正。
本文针对载人月球极地探测任务,采用一种基于自由返回轨道和三脉冲机动轨道的地月转移轨道方案,以保证更高的安全性。其中,关于自由返回轨道部分的设计,以近月点伪参数集为设计变量,提出一种考虑地球扁率修正的改进多圆锥截线法,对自由返回轨道进行两段拼接求解。关于三脉冲机动轨道部分的设计,与上述文献中采用的传统霍曼变轨的方案不同,而是基于混合轨道模型,采用特殊点变轨与Lambert算法相结合的方案。然后运用一种串行求解策略进行轨道设计。仿真结果显示,该策略具有求解精度高、速度增量消耗低的优势。最后,利用该策略进行大量的仿真计算,分析轨道的速度增量特性。
1 地月转移轨道方案描述
针对载人月球极地探测任务,考虑最大限度地保证航天员的生命安全,采用一种自由返回轨道与三脉冲机动轨道相结合的地月转移轨道方案。如图1所示,轨道方案的具体过程如下:首先,从地月转移入射点D出发进入自由返回轨道(Free return orbit, FRO)到达近月点A;其次,在A点施加第一次脉冲进入大椭圆过渡轨道1(Ellipse transition orbit 1, ETO1);然后,在ETO1上的B点施加第二次脉冲进入大椭圆过渡轨道2(Ellipse transition orbit 2, ETO2),B点由ETO1和月球极地轨道(Lunar polar orbit, LPO)的轨道面交线确定,选择离ETO1远月点较近的交点,理想情况下,B点即为ETO2的远月点;最后,在ETO2的近月点C处施加第三次脉冲进入LPO。其中,在B点调整轨道面角度后,从B点到C点的面内转移轨道不采用传统的霍曼转移方式,而是基于Lambert算法进行计算,具体的求解过程在下文进行详细说明。
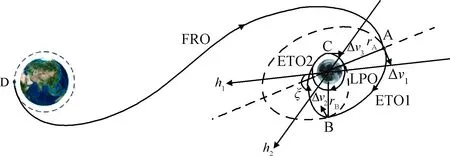
图1 地月转移轨道示意图Fig.1 Earth-Moon transfer orbit
2 轨道设计方法
本节提出一种从初步设计到精确设计的串行求解策略。初步设计阶段,针对自由返回轨道部分,在基于近月点伪参数的两段拼接模型中,采用改进的多圆锥截线法进行计算,针对三脉冲机动轨道部分,在混合轨道模型中,采用特殊点变轨与Lambert算法相结合的方法进行求解;精确设计阶段,以轨道初步设计的结果为初值,在高精度模型中进行精确求解。
2.1 初步设计
2.1.1自由返回轨道
在自由返回轨道的初步设计阶段,选取近月点伪经度λprl、近月点伪纬度φprl、近月点速度方位角iprl和近月点轨道偏心率eprl作为优化设计变量[17]。当给定近月点时刻tprl和近月点高度hprl时,可以基于近月点伪参数集(λprl,φprl,iprl,eprl),建立两段拼接模型,采用改进的多圆锥截线法来完全确定一条自由返回轨道。在本文中,近月点时刻与近月点高度根据任务直接给出。
月心段轨道半长轴为
(1)
式中:rm为月球半径。
月心段轨道近月点速度大小为
(2)
式中:μm为月球引力参数。
当给定iprl时,近月点的位置和速度矢量在月心近月点坐标系中的坐标可以表示为
rprl=[hprl+rm, 0, 0]T
(3)
vprl=[0,vprlcosiprl,vprlsiniprl]T
(4)
近月点的位置和速度矢量在瞬时月心白道系下的坐标表示为
(5)
(6)
进而可以得到近月点的位置和速度矢量在月心J2000坐标系下的坐标为
(7)
(8)
式中:Ωm,im,um分别为tprl时刻月球相对地球的升交点赤经、轨道倾角和纬度幅角。月球轨道根数可以通过JPL星历求得。
因此,近月点在地心J2000坐标系下的位置和速度矢量为
(9)
(10)
式中:rm,vm分别为月球在地心J2000坐标系的位置和速度矢量。
以近月点为界,将自由返回轨道分为两段:从地月转移入射点到近月点为第一段,从近月点出发到真空近地点为第二段。真空近地点为地心段返回轨道的近地点,真空近地点的地心距与再入角和再入点的地心距的近似关系如式(11)所示[27]。因此,自由返回轨道的再入点约束可以等效为真空近地点约束。例如,再入点的高度为122 km,再入角为-6°的约束,可以等效为真空近地点高度为51 km的约束。
rvcp=rpcos2γp
(11)
式中:rvcp为真空近地点的地心距,rp为再入点的地心距,γp为再入角。
以近月点状态为初始状态,分别采用改进的多圆锥截线法进行求解,其中,第一段采用逆向求解思路,第二段采用正向求解思路。转移时间由圆锥曲线拼接法初步给出。下面首先介绍一下改进的多圆锥截线法的主要步骤,图2为改进的多圆锥截线法示意图。

图2 改进的多圆锥截线法示意图Fig.2 Schematic of improved multi-conic method
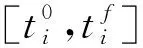


(12)
asi=
(13)
式中:μs为太阳引力常数。
修正步骤(1)得到的地心伪状态
(14)
(15)
式中:Δt为转移时间被分为N段得到的时间步长。
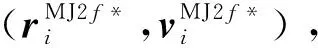
(16)
(17)
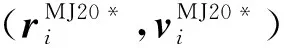
(18)
第二段轨道从近月点正向外推至真空近地点,满足真空近地点条件
(19)
采用二分法重复以上过程,以确定精确的近地出发点和真空近地点的状态。
改进的多圆锥截线法的具体求解过程如图3所示。

图3 改进的多圆锥截线法的流程图Fig.3 Flow chart of improved multi-conic method
自由返回轨道的设计主要满足以下约束
(20)
式中:h0和i0分别为近地出发点的高度和轨道倾角,if和hf分别为真空近地点的轨道倾角和高度,hD和iD分别为D点的高度和轨道倾角,hA为A点的高度,ivcp和hvcp分别为自由返回轨道终点的轨道倾角和高度。
因此,自由返回轨道的整个设计流程如图3所示。
第一步:给出近月点时刻tprl和近月点伪参数集{λprl,φprl,iprl,eprl}初值。
第二步:由式(1)~(10)求得该时刻在地心J2000坐标下的近月点状态。
第三步:采用改进的多圆锥截线法,执行步骤(1)~(5),分别得到近地出发点和真空近地点的状态。
第四步:判断近地出发点和真空近地点的状态是否满足约束,若满足,则停止计算;若不满足约束,则将约束条件设置为目标函数,在当前迭代的近月点伪参数上,结合SQP_Snopt算法进行求解。SQP_Snopt算法是一种改进的SQP算法[28],内置有限拟牛顿法来近似拉格朗日乘子的Hessian矩阵,极大地减少了Hessian矩阵的计算量,从而有效地提高了计算速度,因此常用于求解光滑非线性规划问题。重复第一步至第三步,直到迭代的近月点伪参数最终满足约束停止计算。
2.1.2三脉冲机动轨道
由于三脉冲机动轨道转移时间较长,采用二体轨道模型进行初步计算不易快速收敛到高精度解附近,所以本文采用二体轨道模型与高精度轨道外推模型相结合的混合轨道模型进行初步计算,以提高轨道初步设计的精度。
假设ETO1轨道周期与三脉冲机动轨道转移时间T的比例为α,具体比例参数根据任务直接给出,通常在0与1之间取值,则ETO1的半长轴和偏心率分别为
(21)
(22)
式中:rA为自由返回轨道近月点A的月心距。
根据自由返回轨道在A点的轨道根数,可以得到第一次脉冲矢量Δv1为
(23)
式中:h2为FRO轨道面的单位法线矢量,eA为FRO在A点的偏心率,h2的上标“~”表示该矢量进行叉乘运算的反对称矩阵[29]。
由于在异面转移过程中,轨道面会在摄动影响下发生变化,LPO与ETO1轨道面的交线需要通过插值确定,LPO的初始条件根据具体的载人月球极地探测任务直接给出。将近月点时刻的ETO1和LPO的轨道状态在高精度模型中外推一段时间,得到LPO和ETO1在各时刻下的位置、速度,则在各时刻下,LPO轨道面法线与ETO1位置矢量的夹角为
(24)
式中:h1(t)为t时刻LPO轨道面的单位法线矢量。
根据夹角的正负值变化,确定外推的停止条件,通过插值进一步确定交线的具体位置。如果交线处在ETO1上的真近点角fB小于90°,则得到的交线在ETO1的近月点附近,便需要继续外推至远月点附近。因此,ETO1和LPO在交线处的轨道根数可以确定,进而能够得到ETO1上B点的位置和速度矢量rB,vBETO1。
第二次变轨的脉冲包括改变轨道面角度的脉冲分量Δv21和用于面内变轨的脉冲分量Δv22,在第二次变轨前后的水平航迹角κ和异面差ξ分别为
(25)
(26)
式中:ΩETO1和iETO1分别为ETO1的升交点赤经和轨道倾角,ΩC和iC分别为LPO的升交点赤经和轨道倾角,uETO1为ETO1上B点的纬度幅角。
则用于改变轨道面角度的脉冲在ETO1月心LVLH坐标系中表示为
(27)
从而可以得到改变轨道面后B点的位置矢量rBETO2和速度矢量vBETO2,通过转换得到ETO2的轨道根数。初步计算时,令B点为ETO2的远月点,进而可以确定ETO2的近月点矢量rCETO2。从B点到C点的面内转移轨道不采用霍曼转移方式,而是基于Lambert算法进行求解。其中,当转移的相位角小于180°时,面内转移轨道采用短程Lambert解,否则采用长程Lambert解。
由rBETO2,rCETO2和面内转移时间,根据Lambert算法可以求解得到面内转移轨道在B点和C点的速度矢量vB和vC,则用于面内变轨的脉冲分量为
Δv22=vB-vBETO2
(28)
则第二次脉冲矢量Δv2为
(29)
第三次脉冲矢量Δv3为
(30)
则总速度增量大小为
(31)
2.2 精确设计
在轨道精确设计阶段,以初步设计的结果作为高精度解计算的初值,采用SQP_Snopt算法进行求解。在月心J2000坐标系中,考虑相关摄动因素,高精度轨道模型为:
(32)
式中:R为载人飞船在月心J2000坐标系中的位置矢量;AN为N体引力摄动加速度,这里只需考虑日月摄动,星体间的相对位置通过JPL星历求解;ANSE为地球非球形摄动加速度;ANSM为月球非球形摄动加速度;AR为太阳光压摄动加速度;AD为大气阻力摄动加速度;AP为推力加速度。这里忽略了木星、金星等大行星的摄动,地球潮汐的摄动,以及相对论效应等微小摄动量的影响。
针对自由返回轨道部分,设计变量、约束条件与轨道初步设计时的设置相同,以初步设计的结果作为精确设计的初值,在高精度轨道模型中进行求解。
针对三脉冲机动轨道部分,已知三脉冲机动轨道转移时间T、月球极地轨道的高度hLPO、轨道倾角iLPO和升交点赤经ΩLPO,选取以下变量作为优化设计变量:第一次脉冲Δv1、第二次脉冲Δv2、第三次脉冲Δv3、前两次脉冲施加的时间间隔T12,则一条三脉冲机动轨道可以由此确定,即
Y=f(Δv1,Δv2,Δv3,T12)
(33)
在高精度模型中进行数值积分,最终得到施加第三次脉冲后的轨道根数,约束条件设置为
(34)
式中:iHP,ΩHP,eHP和hHP分别为高精度外推后得到的环月轨道倾角、升交点赤经、偏心率和轨道高度。
在实际工程任务中,通常希望轨道转移过程燃料消耗最少,考虑火箭的运载能力,本文将优化目标设为总速度增量最小
J=(ΔV)min
(35)
3 仿真校验
本节通过仿真算例对上文提出的轨道设计方法的有效性进行校验。首先,针对自由返回轨道,给出一组仿真算例,算例参数设置如下:近地出发点的高度为170 km,轨道倾角为21°,近月点高度200 km,近月点时刻为2028.06.27 10∶50∶00,真空近地点高度为50 km,真空近地点轨道倾角为43°。采用第2节提出的轨道设计方法对自由返回轨道进行求解,同时采用文献[18]中的圆锥曲线拼接方法进行求解,得到的轨道设计结果如表1所示。
从表1可以看出,与文献[18]中的圆锥曲线拼接方法相比,采用初步设计中的改进的多圆锥截线法求解的结果精度更高,与高精度解更为接近。相比于初步设计,高精度轨道模型的摄动因素对再入点的位置有一定的影响,其中,再入点经度的偏差在2°左右,再入点纬度的偏差在0.1°左右,再入时刻的偏差在7 min左右。此外,在仿真中可知,以文献[18]的方法得到的结果为初值进行精确求解时,计算用时在120 s左右,而本文的精确设计的用时在66 s左右。因此,改进的多圆锥截线法虽然增加了初步设计的求解时间,但可以为精确设计提供更好的初值,从而显著减少精确求解的用时,加快高精度解的收敛。因此,针对载人月球极地探测地月转移轨道中的自由返回轨道部分,本文提出的轨道设计方法可以有效地完成高精度解的计算。

表1 自由返回轨道求解结果Table 1 Results of free return orbit
其次,针对三脉冲机动轨道部分,采用轨道初步设计方法进行计算,同时采用文献[24]中的特殊点变轨方法进行求解,将两者结果进行对比。仿真算例参数设置如下:FRO近月点高度为200 km,偏心率为1.5,LPO轨道高度为300 km。三脉冲机动轨道最大转移时间为24 h,α为0.9。图4给出了不同交线位置和异面差对应的第二次脉冲大小等高线图,图5是采用文献方法求解得到的结果。由图4、图5对比可知,在不同的交线位置和异面差的情况下,本文提出的轨道初步设计方法能够有效地减小第二次脉冲的大小,尤其是当异面差较小时,本文的方法体现出的优势更加明显。

图4 第二次脉冲大小的变化Fig.4 The change of the second impulse

图5 第二次脉冲大小的变化(文献[24]方法)Fig.5 The change of the second impulse (Method in reference [24])
将异面差设置为0,改变三脉冲机动轨道最大转移时间,图6给出了不同交线位置和最大转移时间对应的总脉冲大小等高线图,图7是采用文献方法求解得到的结果。通过图6、图7对比可知,在不同交线位置和最大转移时间的情况下,本文提出的轨道初步设计方法也能明显降低面内机动的脉冲大小,尤其是交线位于距远月点较远的位置时,本文的方法对降低面内机动脉冲更加有效。

图6 面内机动的总脉冲大小Fig.6 Total velocity increment of maneuver in orbit plane

图7 面内机动的总脉冲大小(文献[24]方法)Fig.7 Total velocity increment of maneuver in orbit plane (Method in reference [24])
下面采用本文提出的串行求解策略,优化求解完整的载人月球极地探测地月转移轨道。仿真参数设置如下:近月点时刻为2028.06.27 10∶50∶00,求解得到的FRO的相关参数如表2所示,其中,位置和速度参数均在地心J2000坐标系下表示。在月固系下,LPO轨道高度为300 km,轨道倾角为90°,升交点经度为142°。α可在0与1之间任意取值,本算例中取为0.9,三脉冲机动的总时间不超过1天。分别采用本文提出的求解策略和文献[24]中的方法进行求解,其中,在采用文献[24]中的特殊点变轨方法时,各脉冲之间的转移时间根据霍曼转移确定,而在采用本文的求解策略时,前两次脉冲之间的转移时间与特殊点变轨策略中的设置保持一致,后两次脉冲之间的转移时间在三脉冲机动的最大总时间约束范围内可调。求解得到三脉冲机动轨道的高精度解如表3所示,其中三次脉冲矢量均在月心J2000坐标系下表示。

表2 自由返回轨道参数Table 2 Parameters of free return orbit

表3 三脉冲机动轨道求解结果Table 3 Results of three-impulse maneuver orbit
从表3可以看出,针对载人月球极地探测地月转移轨道,本文提出的轨道设计方法能够有效地降低总脉冲消耗,与文献中的方法相比,可以节省大约131 m/s的速度增量。在月心J2000坐标系下,画出完整的高精度轨道,如图8所示。因此,文献[24]中的三脉冲机动方案采用传统的特殊点变轨方式,从第二次脉冲施加位置B点到近月点C点的转移,所需的时间和速度增量的消耗完全由B点位置和LPO轨道高度确定,无法保证最优转移。而由于各种摄动力的影响,B点距离远月点较远,所以消耗的总脉冲较大。而本文通过Lambert算法确定B点与C点之间的最优转移轨迹时,转移时间可调,在满足最大转移时间约束下,通过寻优求解,相比传统的霍曼转移方式,该方法可以在较短的时间内完成最优转移,并且消耗的总脉冲较小。
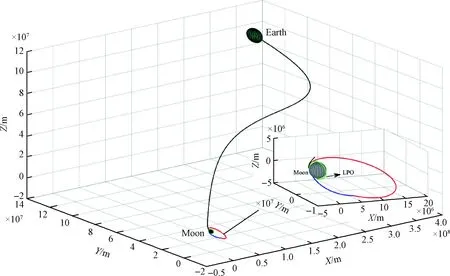
图8 高精度轨道Fig.8 High-fidelity orbit
4 速度增量特性分析
在载人月球极地探测方案设计阶段,掌握一类轨道的特性,对后续制定方案具有十分重要的意义。而在工程实际中,速度增量是比较关心的一个指标。本节采用上文提出的轨道设计策略,通过大量计算仿真,对地月转移轨道的速度增量特性进行分析。
4.1 升交点经度的影响
FRO参数与第3节设置相同,LPO的轨道高度与倾角也保持不变,改变LPO在月固系下的升交点经度,分别计算通过三脉冲机动到达不同LPO所需的速度增量。速度增量随LPO升交点经度的变化情况如图9所示。从图9可以看出,速度增量随着升交点经度的增加,呈现先增加后减小的趋势,当升交点经度为90°时,速度增量达到最大,约2400 m/s,当升交点经度为180°时,速度增量最小,约为1200 m/s,符合文献[30]中得到的三脉冲机动方案在2600 m/s速度增量范围内可实现全月面到达的结论。由此可知,当LPO升交点、降交点连线方向与地月连线方向垂直时,地月转移轨道对燃料消耗的要求较高,而当LPO升交点、降交点连线方向与地月连线方向接近时,地月转移轨道对燃料消耗的要求较低。因此,在实施载人月球极地探测任务时,可以选择升交点、降交点连线方向与地月连线方向接近的LPO作为目标环月轨道。

图9 速度增量与LPO升交点经度的关系Fig.9 Velocity increment versus longitude of the ascending node of LPO
4.2 转移时间的影响
改变三脉冲机动轨道转移时间,其它参数与第3节中设置相同,计算在不同三脉冲机动轨道转移时间下,地月转移所需的速度增量。如图10所示,速度增量随着转移时间的增加而逐渐减小。当转移时间在12~24 h变化时,速度增量变化幅度较大,约为200 m/s。当转移时间大于30 h时,速度增量下降幅度不大,在18 h的变化区间内,速度增量仅仅减少了约50 m/s。因此,考虑航天员的生命安全以及转移过程中产生的其它能源消耗的成本,可以选择24~30 h的三脉冲机动轨道方案。

图10 速度增量与转移时间的关系Fig.10 Velocity increment versus transfer time
4.3 月球极地轨道高度的影响
改变LPO的高度,同时设置FRO近月点高度与LPO高度保持一致,其它参数与第3节中设置相同,计算到达不同轨道高度的LPO时,地月转移需要的速度增量。如图11所示,随着月球极地轨道的轨道高度的增加,速度增量不断减少,当LPO的轨道高度从200 km增加到1600 km时,速度增量降低约160 m/s。因此,在满足其它月球极地探测条件的情况下,可以选择轨道高度较高的LPO。

图11 速度增量与LPO轨道高度的关系Fig.11 Velocity increment versus LPO altitude
4.4 ETO1轨道周期的影响
改变ETO1轨道周期,即改变比例参数α,其它参数与第3节中设置相同,计算不同比例参数下,三脉冲机动所需的速度增量。如图12所示,随着比例参数的增加,ETO1轨道周期不断增大,速度增量不断减小。因此,在进行三脉冲机动时,可以选择轨道周期较长的ETO1轨道。

图12 速度增量与比例参数的关系Fig.12 Velocity increment versus α
5 结 论
本文针对载人月球极地探测任务,采用了一种自由返回轨道与三脉冲机动轨道相结合的地月转移轨道方案,并提出一种从初步设计到精确设计的串行求解策略进行优化设计。在基于近月点伪参数的两段拼接模型中,采用改进的多圆锥截线法对自由返回轨道进行初步设计,能够有效地提高初步设计的精度。采用特殊点机动与Lambert算法相结合的方法对三脉冲机动轨道进行优化设计,与已有文献的方法相比,可以有效地减少速度增量的消耗。在实际任务中,若考虑较少的速度增量消耗,可选择升交点、降交点连线方向与地月连线方向接近,且轨道高度较高的月球极地轨道作为目标环月轨道,三脉冲机动轨道的转移时间可以设置为24~30 h,并选择轨道周期较长的ETO1进行转移。

