运载器式潜射导弹水面分离运动特性

陆辰昱，王 鑫，周志坛，梁晓扬，乐贵高

(1. 南京理工大学机械工程学院，南京 210094；2. 中国人民解放军96901部队，24分队，北京 100094)

0 引 言

潜射导弹的发射方式目前主要有两种：湿式发射和干式发射。采用干式发射时，运载器包裹着导弹在水下航行。期间导弹不与水直接接触，并且大部分水动力载荷由运载器承担。当运载器穿过水面时，导弹助推器点火推动其与运载器分离，转入空中飞行弹道[1]。弹器分离阶段虽然时间短，却提供了导弹空中飞行的初始条件，是发射成功的关键[2-3]。然而分离过程在自由液面进行，受海浪和多体相互作用等因素影响，分离运动呈现很强的非线性。因此，有必要对运载器式潜射导弹水面分离运动特性加以研究。

目前国外关于多体出水分离运动的研究较少，关注更多的是单体跨介质运动[4-5]和空中多体分离问题[6-8]。而国内则有较多学者开展了飞行器出水分离的相关研究。彭正梁等[9]建立了高速航行体与运载器水面分离的线性多体动力学方程，并基于势流理论计算了水动力，进而对该过程进行了二维弹道仿真；顾媛媛等[10]基于切片法建立了航行器水面分离的动力学模型，并通过Matlab进行数值模拟，研究了分离过程中航行器的运动参数变化；李晶等[11]对筒式导弹出水分离过程进行了研究。通过受力分析建立了多体动力学方程，进而计算了分离过程中姿态和速度等参数的变化；刘曜等[12]通过构建动力学方程组对潜射导弹的水下弹道和水面分离弹道进行了仿真研究，并通过与水洞试验对比验证了计算模型的精确性。以上研究为运载器式潜射导弹水面分离过程的预测提供了一定的参考依据。然而，目前绝大多数研究缺乏对液体相的模拟，且在处理水动力问题时均采取如势流理论等简化的液体流动模型。实际情况下，运载器出水分离伴随着海浪的扰动以及波浪的破碎，其受力情况较为复杂。因此，需要在计算运载器与导弹分离运动的同时，精确地模拟自由液面的状态。

本文建立了自由液面模型和六自由度运动方程，并将以上多介质耦合模型的计算结果与实验数据对比。在验证了计算模型的精度和有效性基础上，对不同海况以及出水角度下运载器式潜射导弹水面分离过程中的质心位移，姿态角及轴向速度等进行了三维仿真计算。本文的数值方法和仿真结果可以为水面分离系统的设计提供指导。

1 分离过程与坐标系建立

如图1所示，运载器在水下发射出筒后依靠惯性和浮力上升，随后冲出水面。此时运载器盖中传感器获得信号，继续上升一段距离后运载器顶盖抛落，随后导弹助推器点火产生推力，推动导弹向上运动。同时，运载器受反推力作用落入水中，完成运载器式潜射导弹的水面分离[13]。在此过程中如图2建立固定坐标系o0x0y0z0，运载器移动坐标系o1x1y1z1，导弹移动坐标系o2x2y2z2。初始时刻(t=0 s)移动坐标系与固定坐标系保持平行。其中o0位于初始时刻运载器顶端中心，o1位于运载器质心，o2位于导弹质心。o1z1与o2z2分别沿着运载器与导弹轴线方向。记运载器动坐标系及导弹动坐标系与固定坐标系之间的欧拉角为滚转角φ，俯仰角θ，偏航角ψ。

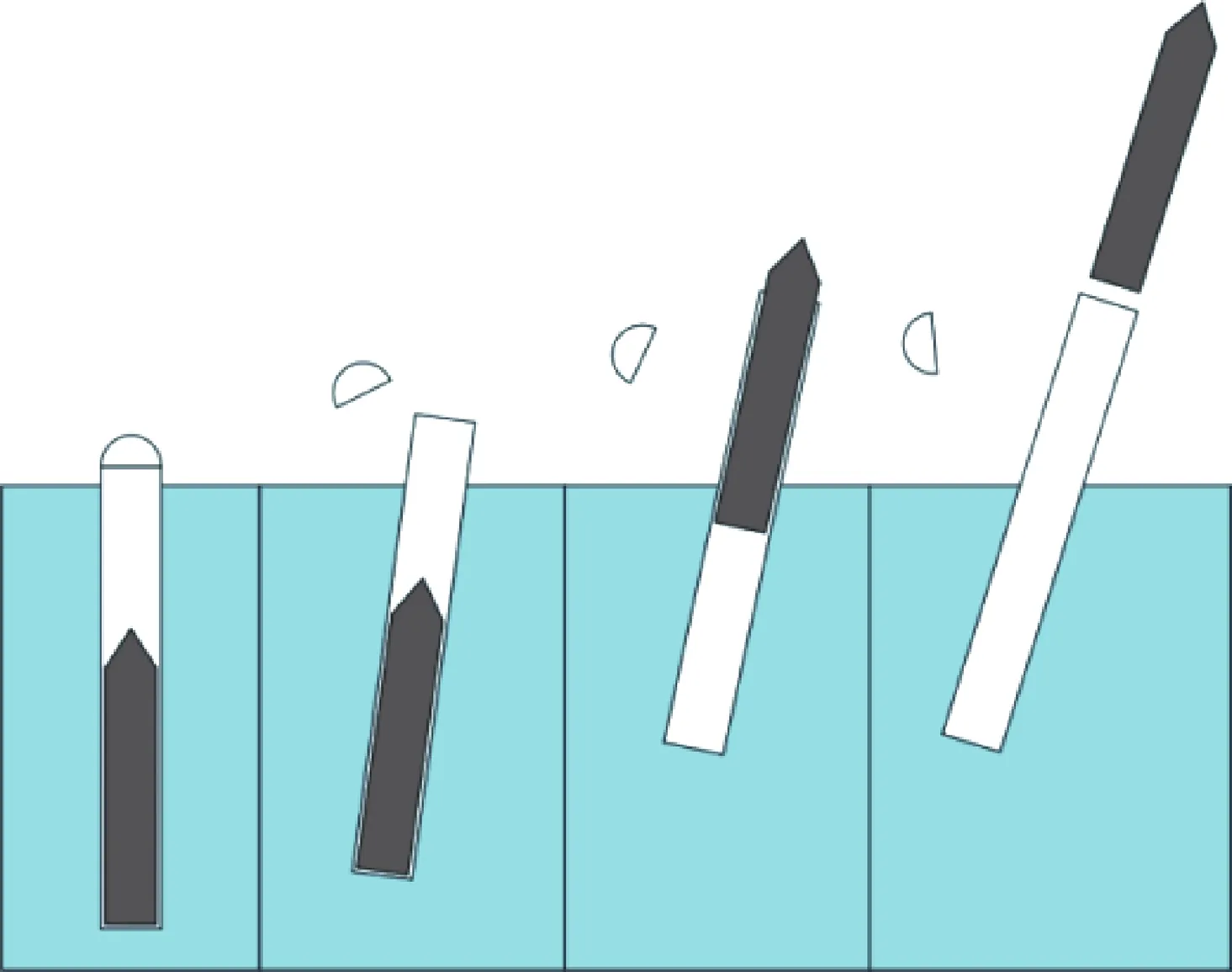
图1 运载器式潜射导弹水面分离过程示意图Fig.1 Schematic diagram of separation process of sub-marine launched missile near the free surface

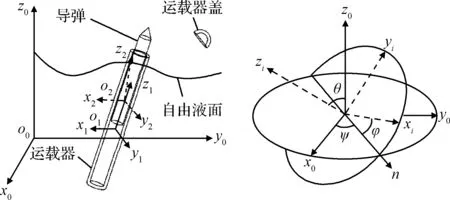
图2 坐标系示意图Fig.2 Schematic diagram of coordinate systems

2 计算模型

如图3所示，运载器式潜射导弹采用单筒单弹结构。运载器直径为1 m，长度为10 m，材料密度为500 kg/m3；导弹直径为0.6 m，长度为6 m，材料密度为1000 kg/m3；运载器初始出水速度为10 m/s；导弹在运载器出水后0.5 s开始点火产生推力，推力大小为100 kN，同时，运载器受到同样大小的反向推力。为了适应运载器与导弹的姿态分布并充分模拟波浪的传递过程，需要较大的计算域。

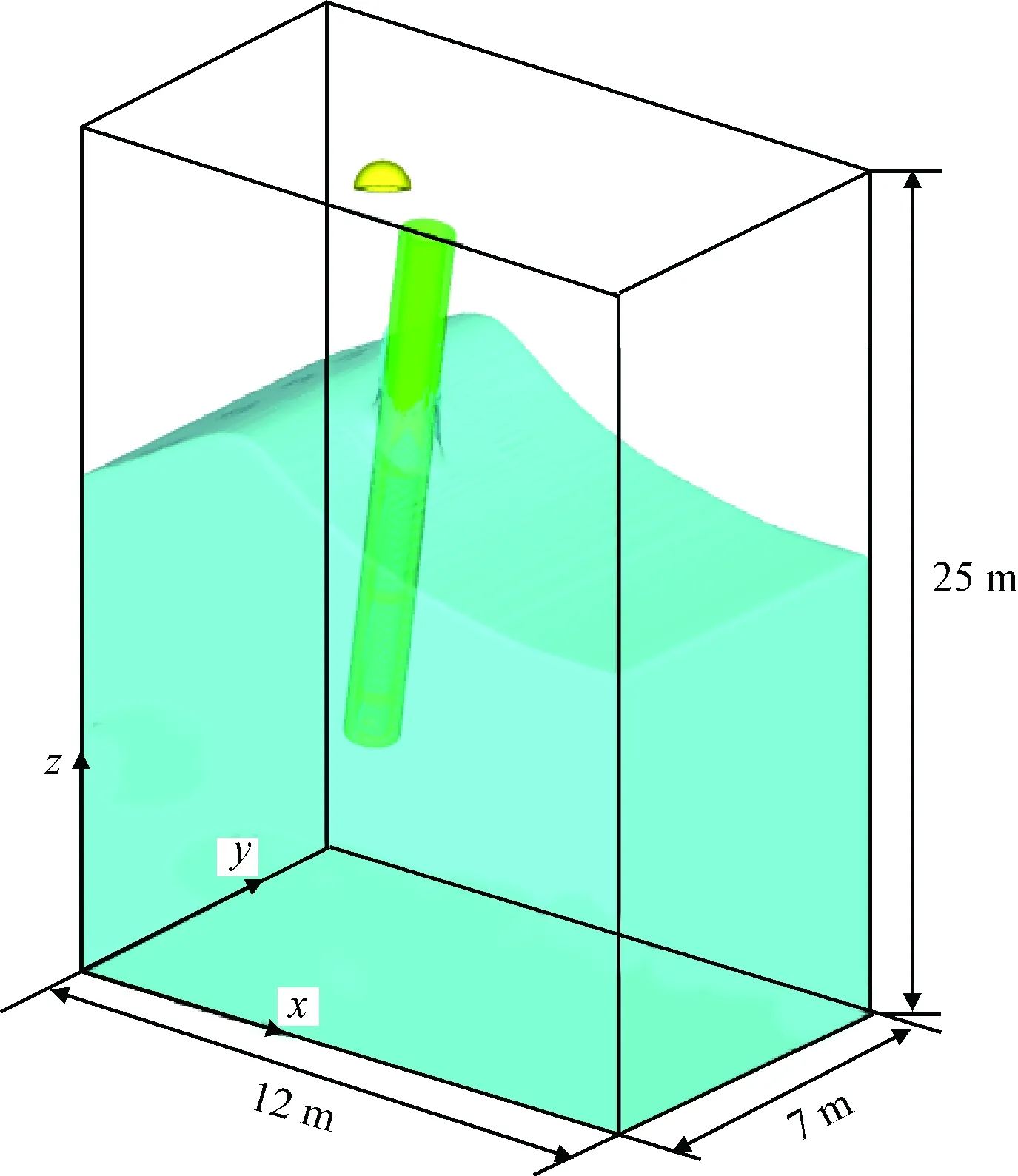
图3 水面分离计算模型Fig.3 Computational model of separation near the free surface

本文为了研究海面波浪以及出水角度对运载器式潜射导弹水面分离运动特性的影响，共设立三组计算工况如表1所示。其中工况2与工况3均采用5级海况下的浪高。

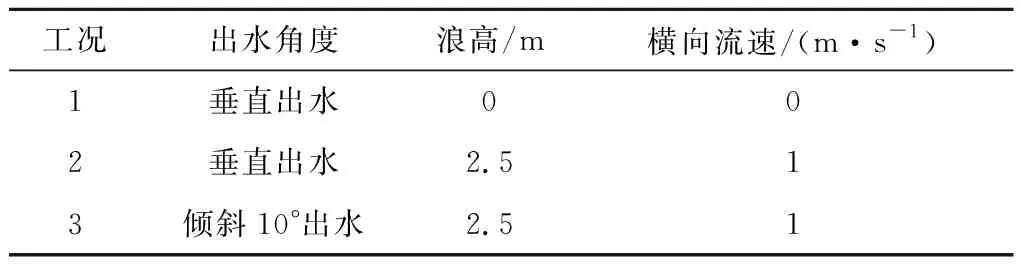
表1 计算工况Table 1 Computational conditions

3 数值方法

3.1 自由液面模型

基于分数容积障碍法(FAVOUR)[14]，建立笛卡尔坐标系下的三维不可压缩Navier-Stokes方程，形式如下：

(1)

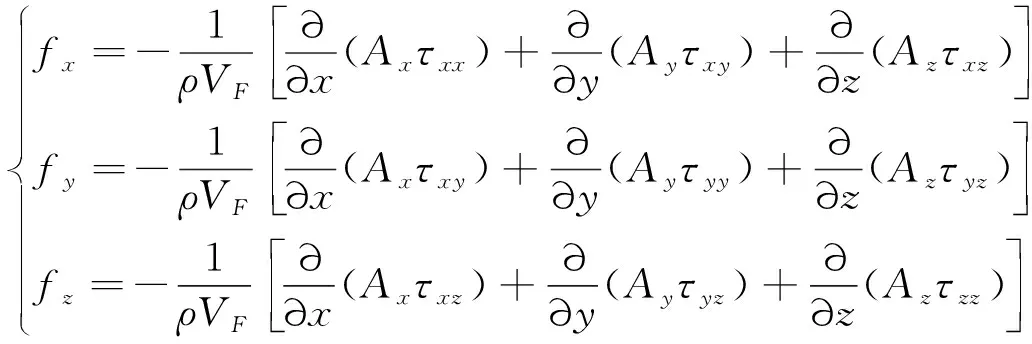
(2)

(3)

式中：ρ为流体密度；u，v，w分别为流体速度在x，y，z方向上的分量；Ax，Ay，Az分别为流体在x，y，z方向上的面积分数；VF为流体的体积分数；p为流体压强；Gx，Gy，Gz为重力加速度；fx，fy，fz为黏滞力加速度。

湍流模型采用RNGk-ε湍流模型[15-16]，与标准k-ε模型相比，它更适于描述有强剪切区域的流动，因此可以更精确地计算水面波浪破碎过程。其中湍动能k方程为：

(4)

式中：ui，uj为xi，xj方向上的速度分量；μ为流体黏度；μt为动力黏度；Gk为平均速度梯度引起的湍动能k的产生项；常数系数σk=1.39。

湍动耗散率ε方程为：

(5)

(6)

对自由液面采用由Hirt等[17]提出的流体体积函数(VOF)进行求解。通过计算网格单元中流体和网格体积比函数F(x,y,z,t)来确定自由液面边界。函数F满足如下控制方程：

(7)

3.2 六自由度运动方程

假设运载器和导弹均为刚体，则其一般运动可分为平移与转动。因此，分离运动方程形式如下：

(8)

式中：F为刚体所受的总外力，m为刚体质量，V为质心速度，T为作用在质心的总力矩，ω为刚体角速度矢量，J为刚体动坐标系下的惯性张量。

若定义B为运动刚体表面上的任意一点，则该点速度可由下式计算：

VB=V+ω×rB

(9)

式中：rB为质心到B点的矢量。

基于FAVOR法和流体连续性方程，刚体运动的控制方程如下[18]：

(10)

式中：Vc为网格单元的体积；SB，n，VB分别为网格单元内运动物体的表面积、单位法向量和速度。

对于刚体之间的碰撞运动采用Stronge[19]提出的多体动力学方程进行求解。假设碰撞过程无摩擦，两碰撞体的质量为M和M′，其质心分别位于点G和G′，碰撞接触点分别为C和C′。在接触点建立碰撞参考系n1n2n3。其中,n1和n2位于公共切面，n3沿着公共切面的法线方向。根据爱因斯坦求和公式，接触点C和C′之间的相对速度vi可由下式计算：

(11)

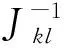
3.3 数值模型关系与计算精度

通过上述模型可在每一个时间步内完成流体与刚体的计算。各模型之间的数值传递关系如图4所示。数值模拟过程采用有限差分法对控制方程进行离散处理，并在时间和空间上保持一阶计算精度。

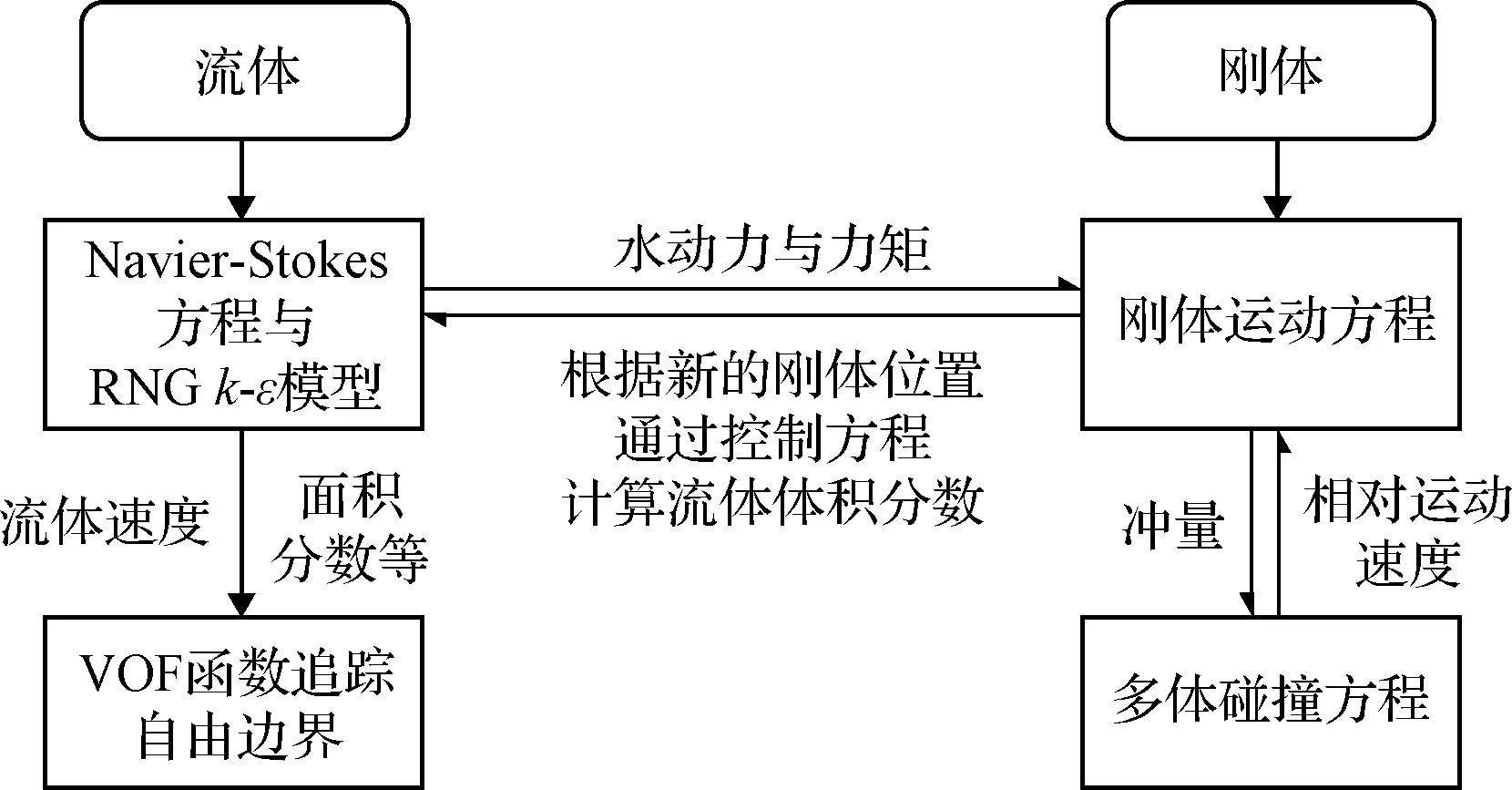
图4 数值模型关系Fig.4 Relationship between numerical models

3.4 模型验证

根据上述自由液面模型与六自由度运动方程，如表2所示，对不同初始倾斜角度的圆柱入水过程进行计算，并与实验结果[20]对比以验证模型的精确性。圆柱的长径比为4，密度为900 kg/m3。圆柱初始入水速度垂直向下。受实验误差影响，其数值略有波动。

图5显示了初始倾角为55.6°，5个不同时刻下，计算结果的速度云图与实验高速摄影图的对比情况。从图5可以看出,两者各时刻圆柱的倾角基本一致，且圆柱两端由于高速入水产生的空泡外形也较为相似。图6显示了初始倾角为55.6°，圆柱入水过程中质心位置和质心垂直速度的计算值与实验测量值的变化曲线。从图6可以看出，计算结果的质心位置与实验结果较为吻合。同时，两者的质心垂直速度也基本一致，仅在末端出现轻微误差。这主要是受计算网格限制，无法完全模拟空泡拉断过程中的细小气泡而造成。

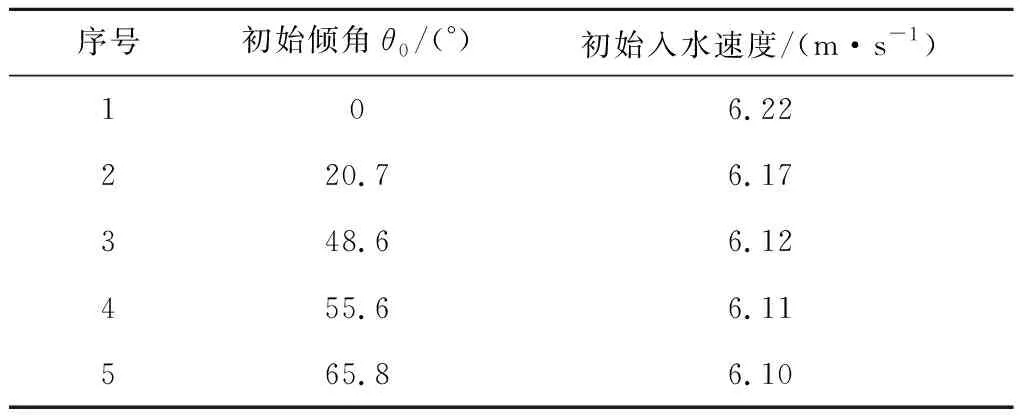
表2 圆柱入水初始条件Table 2 Water entry conditions of the cylinder

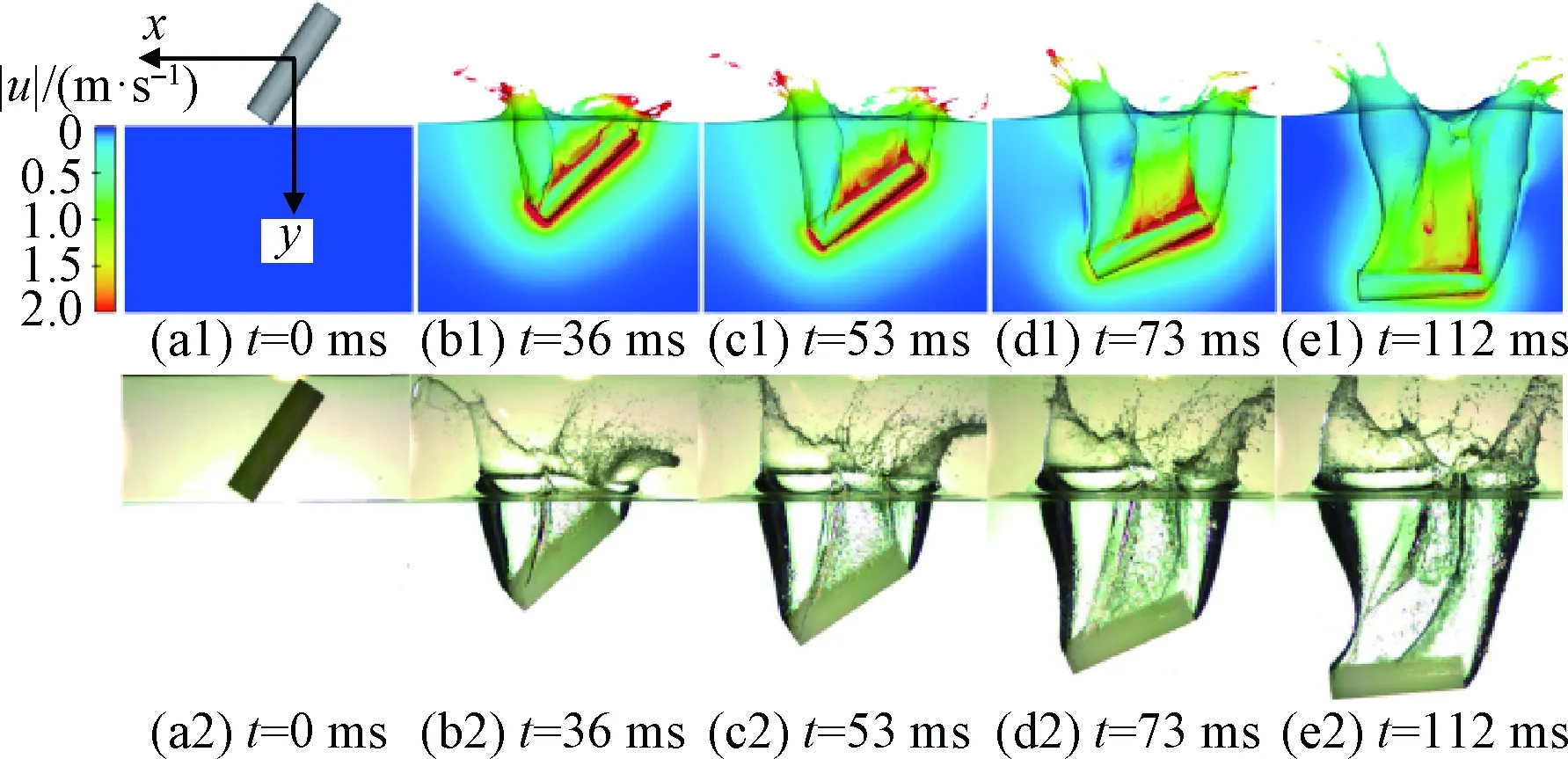
图5 速度场计算结果与实验高速摄影图像(θ0=55.6°)Fig.5 Calculated results of velocity magnitude and high-speed photographs(θ0=55.6°)

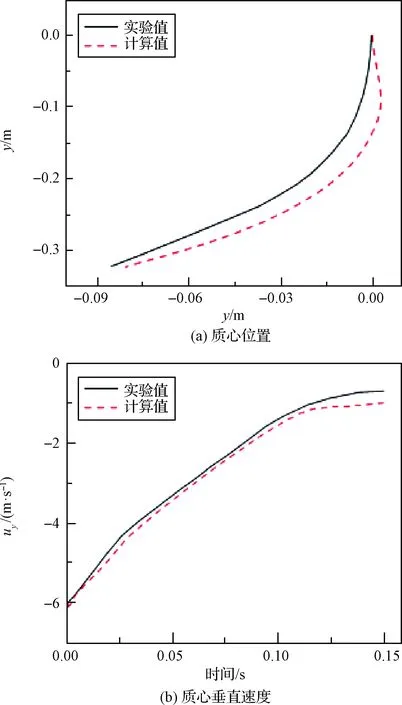
图6 质心位置与质心垂直速度对比(θ0=55.6°)Fig.6 Comparison of mass center position and comparison of mass center vertical velocity(θ0=55.6°)

在此基础上，对其余初始倾角的工况也进行了对比计算。如图7所示，不同初始倾角下圆柱入水，在100 ms时两端的空泡形状仍较为相似。同时，从图8可以看出，计算得到的圆柱入水角位移曲线与实验值保持较好的吻合。综上，仿真模型具有较高的精度。

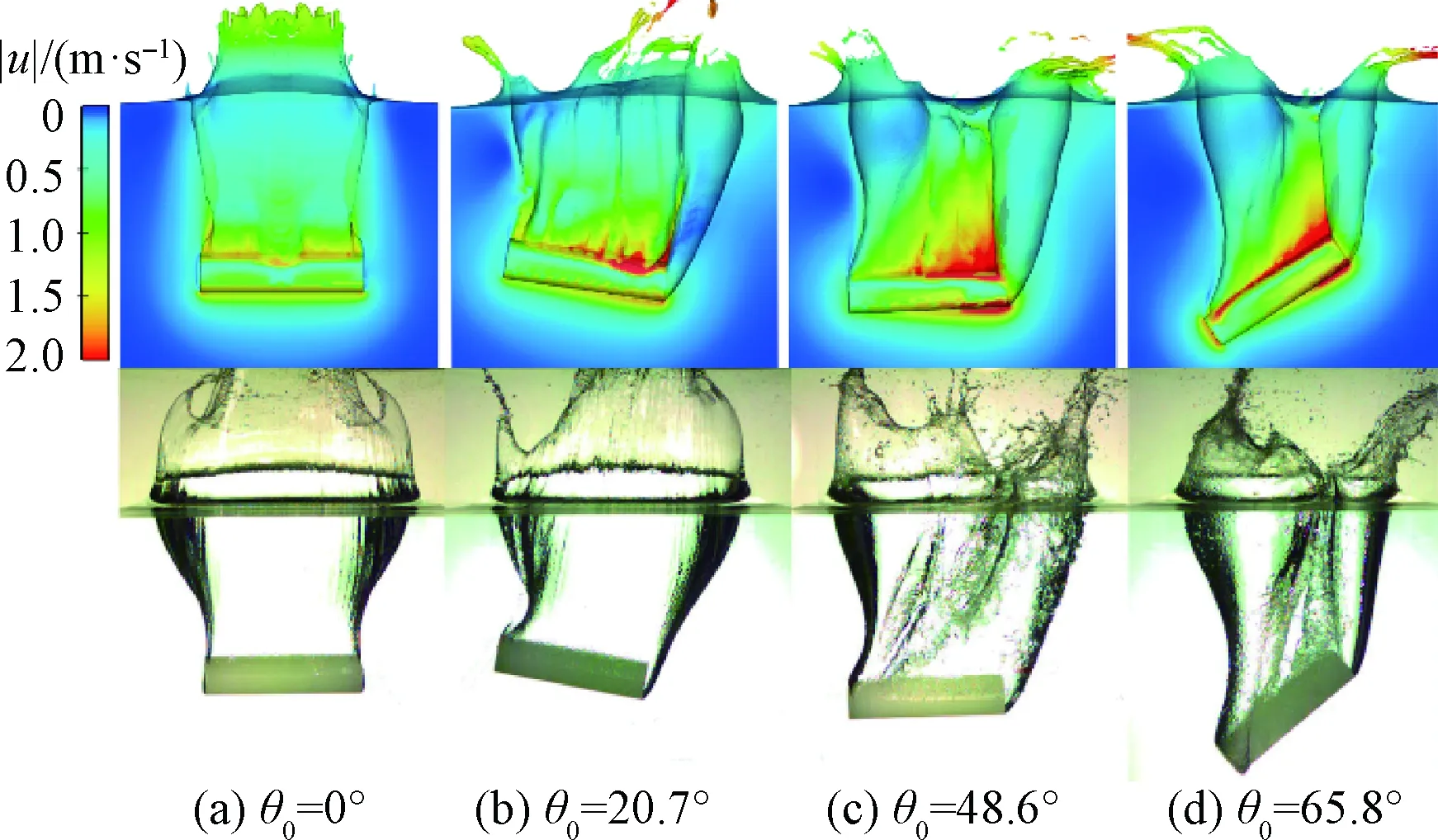
图7 速度场计算结果与实验高速摄影图像(t=100 ms)Fig.7 Calculated results of velocity magnitude and high-speed photographs (t=100 ms)

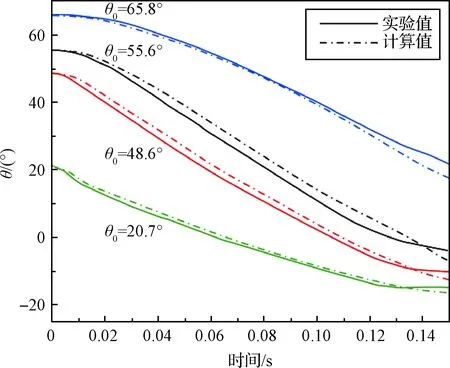
图8 不同初始倾角下圆柱入水角位移对比Fig.8 Comparison of angular displacement for the water entry with different initial inclined angles

4 计算结果及分析

4.1 分离状态

图9为各工况下y+方向的分离状态图像序列。由图9可知，从t=0.5 s导弹产生推力开始，工况1～3均在1.03 s完成分离过程。其中，工况1由于海面无波浪且海水横向流速为0 m/s，运载器与导弹在分离后仍能保持相对垂直的姿态。而工况2在5级海况下进行分离，虽然分离时间较短，运载器和导弹仍由于波浪冲击产生较大的倾角。由图9(c)可知，工况3虽然与工况2的分离环境相同，但由于运载器初始时刻倾斜10°出水，在分离结束后运载器与导弹最终偏转到垂直姿态。而垂直姿态更有利于导弹的弹道控制，实施全方位攻击。因此，若能控制运载器以一定角度出水，则在较高海况等级下导弹仍能在分离后获得较好的初始状态。

4.2 质心位置

图10和图11显示了各工况下运载器与导弹在分离过程中的质心位置。其中，工况2下由于受波浪推动，运载器与导弹质心均在x方向有较大位移。而由于出水瞬间外部载荷急剧变化，工况1,2,3中运载器质心均在y方向上有轻微晃动。其中工况3由于运载器倾斜出水，受波浪扰动力大，运载器与导弹质心在y方向位移相对较大。此外，各工况下运载器受反推力作用，从0.8 s开始其质心在z方向高度不再上升，转而落入水中。且同一时刻下，工况3中运载器与导弹质心在z方向位置较工况1与工况2略高。可以推断，此时波浪对运载器有一定的向上推动作用。

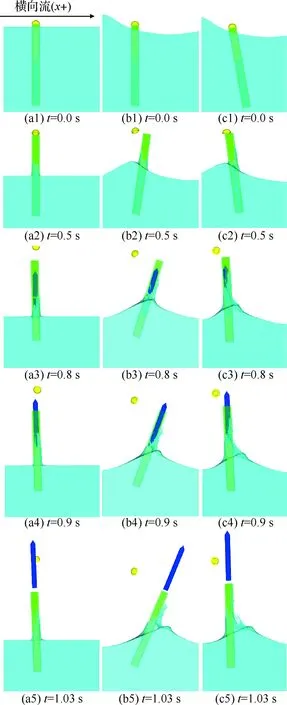
图9 工况1(a)，工况2(b)，工况3(c)分离状态图像序列Fig.9 The image sequence of separating state in working condition 1(a), 2(b) and 3(c)

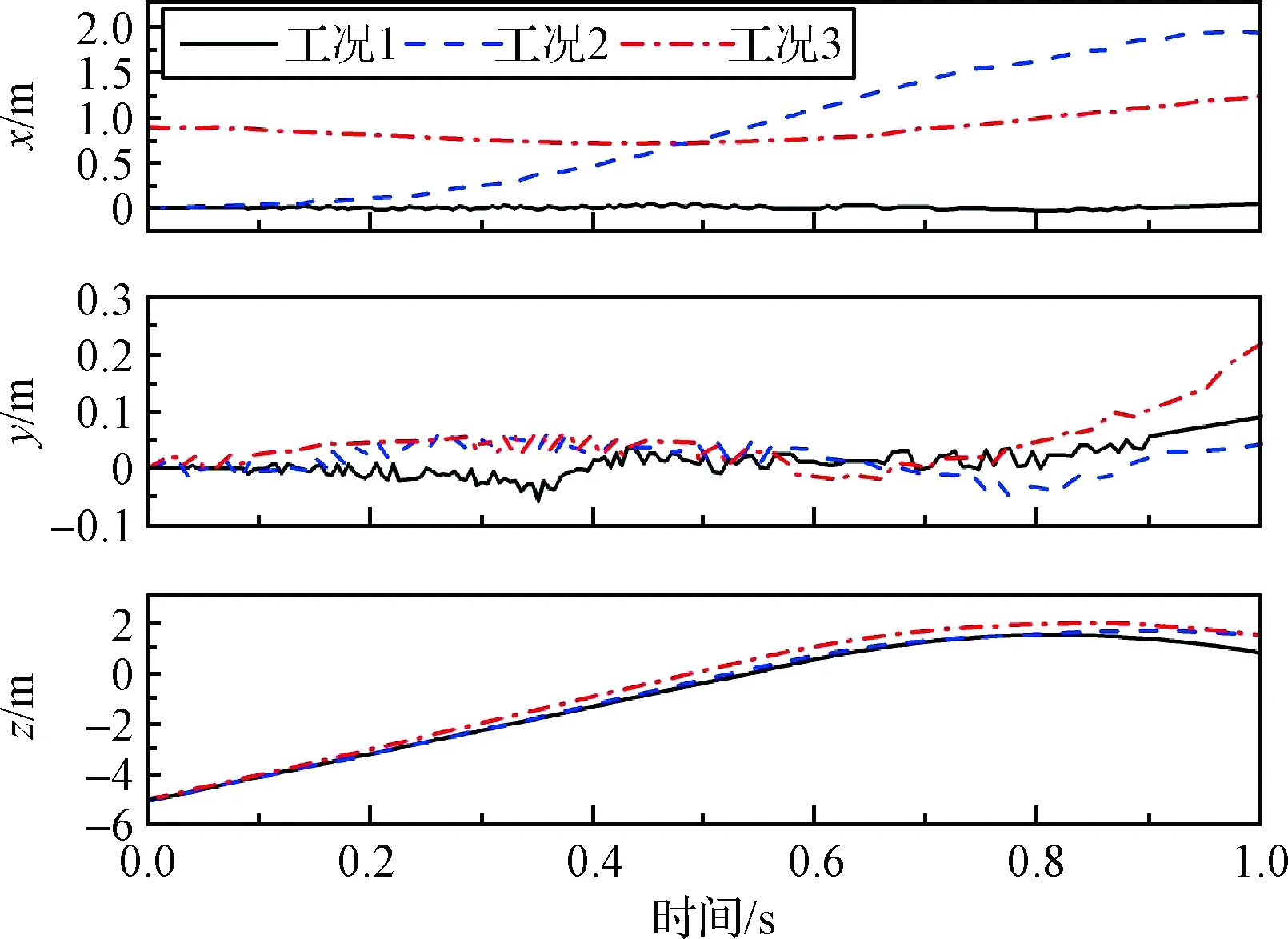
图10 运载器质心位置Fig.10 Mass center position of launch canister

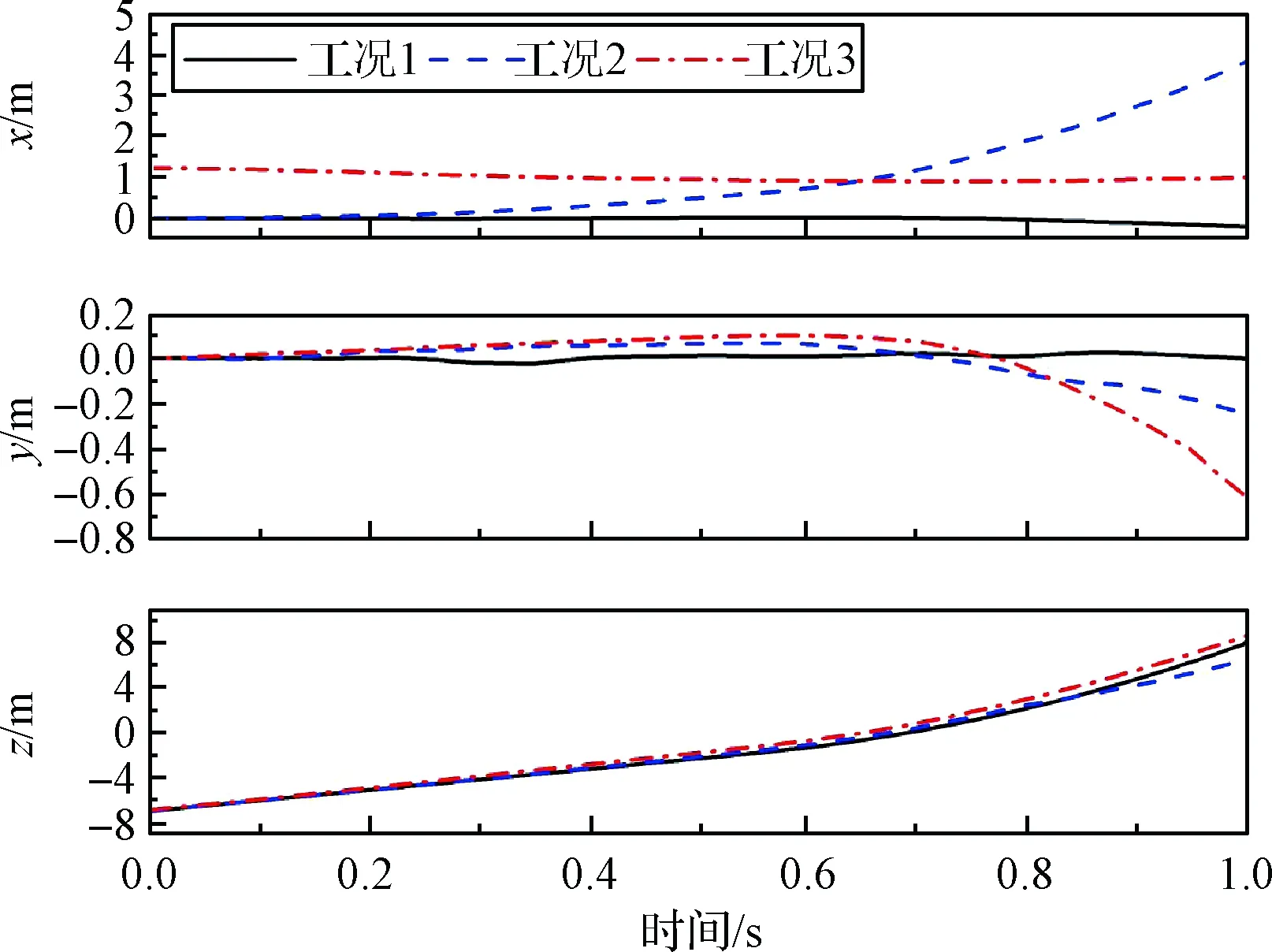
图11 导弹质心位置Fig.11 Mass center position of missile

4.3 姿态角

图12和图13为各工况下运载器与导弹在分离过程中的姿态角。从图12～13可以看出，工况1下，运载器与导弹各姿态角变化数值较小。而工况2受海面波浪影响，各姿态角显著增大。其中运载器与导弹的滚转角φ和俯仰角θ从0.2 s受到波浪冲击力后逐渐增大，而偏航角ψ从0.5 s导弹点火产生推力开始才逐渐增大。工况3下，由于倾斜出水，受波浪干扰力大，运载器与导弹的滚转角φ相对较大。而运载器与导弹的俯仰角θ从最开始的-10°偏转回0°左右。各工况下姿态角的最大绝对值如表3所示。其中工况2下运载器与导弹俯仰角最大绝对值达到22°左右。虽然仍在发射允许的安全范围内，但若浪高进一步增加，导弹有倾覆的危险。

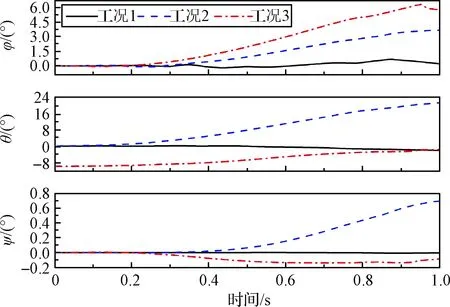
图12 运载器姿态角Fig.12 Attitude angles of launch canister

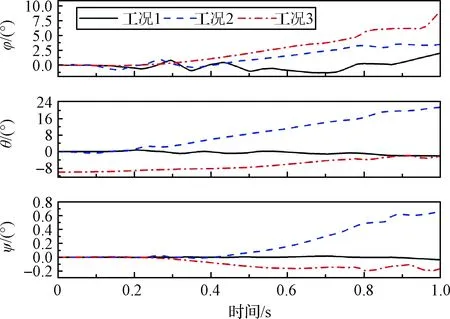
图13 导弹姿态角Fig.13 Attitude angles of missile

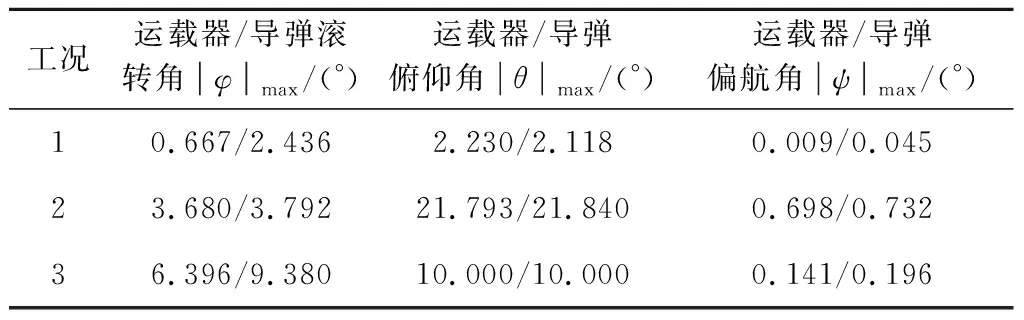
表3 各工况下姿态角最大绝对值Table 3 Maximum absolute value of attitude angles under each working condition

4.4 轴向速度

图14与图15为各工况下运载器与导弹在分离过程中的轴向速度。如图14所示，各工况下，0.5 s即导弹点火前，运载器轴向速度均保持在10 m/s左右。随后运载器受反推力作用轴向速度降低到-7 m/s左右。整个分离过程中，运载器轴向速度由正到负，最终落入水中。其中工况2由于运载器俯仰角相对较大，受波浪的推动，反向速度增加相对较慢。由图15可知，导弹受运载器保护，各工况下其轴向速度基本一致。因此，导弹轴向速度不受波浪与出水角度的影响，且导弹分离完成后的轴向速度均达到35 m/s左右，满足出筒速度的要求。

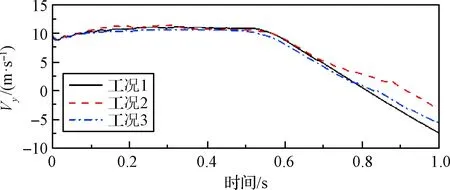
图14 运载器轴向速度Fig.14 Axial speed of launch canister

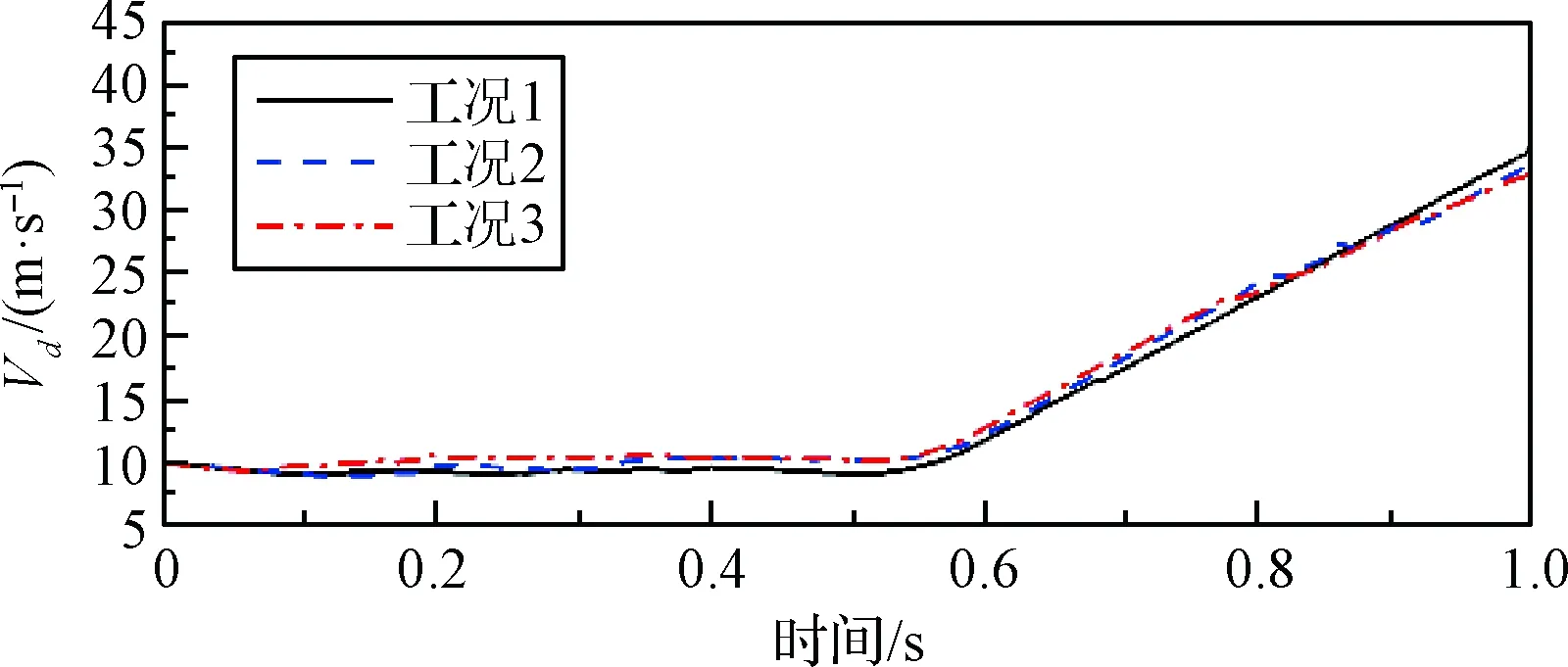
图15 导弹轴向速度Fig.15 Axial speed of missile

5 结 论

本文建立了自由液面模型与六自由度运动方程，并通过与试验数据对比验证了模型的精度。在此基础上对不同海况以及出水角度下运载器式潜射导弹水面分离的运动特性问题进行了三维数值模拟，主要结论如下：

1)各工况下运载器式潜射导弹均在出水后1.03 s左右完成分离。分离过程中，运载器在y方向上存在轻微晃动。各工况下运载器与导弹的姿态角与轴向速度变化较为稳定，且均在安全范围内，证明了该种分离方式的优越性。

2)波浪除了推动运载器与导弹在横向流速的方向产生一定位移外，其影响主要体现在对姿态角散布范围的增大。其中，增加最为明显的为俯仰角。在5级海况下，运载器与导弹俯仰角的最大绝对值达到22°。

3)控制运载器以一定角度出水可以保证导弹分离后的相对垂直姿态，但由于倾斜出水受波浪扰动力大，运载器与导弹的滚转角增大，相应的其在y方向上的位移也有所增大。