空间绳网有控展开方法及优化
司骥跃,庞兆君,杜忠华,冯广斌
(南京理工大学机械工程学院,南京210094)
0 引 言
面对日益严峻的空间环境问题,空间绳网抓捕技术被认为是一种有前景的空间碎片主动清除技术[1-2]。最常见的空间绳网抓捕系统通过母平台发射若干个牵引体带动折叠的空间绳网展开,绳网与母平台之间有拖曳绳连接。之后空间绳网朝向抓捕目标飞行并与目标接触,在收口装置的作用下对目标形成可靠包裹。最终由母平台通过拖曳绳将目标拖离至坟墓轨道,实现空间碎片主动清理[3]。
本文重点研究空间绳网展开阶段的性能优化问题。由于空间实验高难度和高成本的制约,现阶段人们主要通过数值仿真的方法对处于空间环境中的绳网展开过程进行研究。空间绳网的动力学建模方法主要有弹簧质点法[4-6]和绝对节点坐标法[7-8]。尽管有研究表明描述绳网内部节点的运动时,绝对节点坐标法相比弹簧质点法存在一些优势。但是由于绝对节点坐标法的单元具有更多的自由度,其计算效率远低于弹簧质点法,并且在绳网展开阶段弹簧质点法也能够较好的模拟绳网的运动过程[8-9]。对绳网展开阶段进行研究并掌握空间绳网的展开规律,可以帮助设计人员确定绳网最佳抓捕时机,对于发射参数的设计也有重大的指导意义。
近年来,国内外学者对空间绳网的展开动力学问题进行了研究,主要集中在绳网展开阶段的动力学建模和绳网展开参数的敏感性分析。陈钦等[10-11]较早地使用弹簧质点法建立了空间绳网的动力学模型,并研究了发射角度和阻尼系数对绳网展开过程的影响。张青斌等[12]基于弹簧质点法建立了考虑空气阻力的绳网动力学模型,并对绳网展开阶段的天地差异进行了研究。于洋等[7]分析了发射速率、发射角度和牵引体质量占比对绳网展开性能的影响,并根据数值仿真结果给出了绳网系统的发射参数选择建议。李京阳等[13]、刘海涛等[14]也进行了类似的研究。国外方面,Salvi等[15]引入质量系数衡量绳网的展开质量,并研究了发射速率、发射角度和绳网构型等对绳网展开质量的影响。Shan等[9]分别使用绝对节点坐标法和弹簧质点法对柔性绳网展开阶段的运动过程进行仿真,分析了多种初始条件对绳网展开的影响。Botta等[16]基于能量和动量分析对绳网展开动力学问题进行了研究,同时以最大展开面积、展开时间和有效时间为目标开展了绳网展开阶段的敏感性分析。
尽管上述文献对绳网展开过程中输入输出参数的变化规律进行了讨论,并根据规律在绳网输入参数设计方面给出了建议。但是现阶段针对提升绳网展开性能方法的探索并不多。高庆玉等[17]借鉴降落伞“先拉出、后展开”思想,提出了一种空间绳网二级发射模式,其研究表明二级发射模式下绳网的最大展开面积以及飞行距离均优于传统的绳网抛射模式。陈青全等[18]提出一种基于“定力撕裂带”的网型控制方法,通过在绳网边线安装定力撕裂带来抑制绳网的回弹现象,研究结果表明选取适当的撕裂力能够提升绳网的展开性能。
本文使用绳网质心和牵引体质心描述绳网展开过程中的回弹现象,将抑制绳网回弹转变为抑制绳网对牵引体的质心追逐。由此提出通过拖曳绳对展开过程中的绳网施加控制力,降低绳网质心对牵引体质心的追逐,以提高绳网的展开性能。使用弹簧质点法建立了绳网的动力学模型,并基于遗传算法得到了最优的控制力曲线,通过数值仿真验证了有控展开相比于无控展开的优势。
1 空间绳网有控展开原理
1.1 绳网展开的质心追逐现象
绳网的展开过程是指折叠储存在网包内的绳网在具有一定初速度的牵引体的拖动下,逐渐从网包内抽出并展开的过程。本文将绳网的展开面积定义为4个绳网网角所围成四边形的面积,将绳网的展开面积与设计面积的比值定义为展开率。绳网展开率的变化规律是评估绳网抓捕能力和确定绳网抓捕时机的重要因素。绳网的展开过程按照其展开率的变化规律可以分为两个阶段:第一个阶段绳网在牵引体的带动下逐渐展开,绳网网口面积由小变大;展开率到达最大值后进入第二个阶段,即回弹阶段。绳网被牵引体拉紧,绳网中心由凹变凸,有逐步赶超牵引体的趋势,四个牵引体逐步收拢,绳网展开率逐渐下降。绳网的回弹造成了网口面积过早减小,降低了绳网的展开性能。所以,可以通过抑制回弹现象提高绳网的展开性能。
为了实现对绳网回弹的抑制,本文首先将空间绳网离散为牵引体及绳网本体,利用两者的质心变化历程描述绳网的回弹现象。图1绘制出了具有正方形网格的四边形绳网的展开率随时间的变化历程及牵引体质心、绳网本体质心的运动历程,仿真输入条件同第4节。
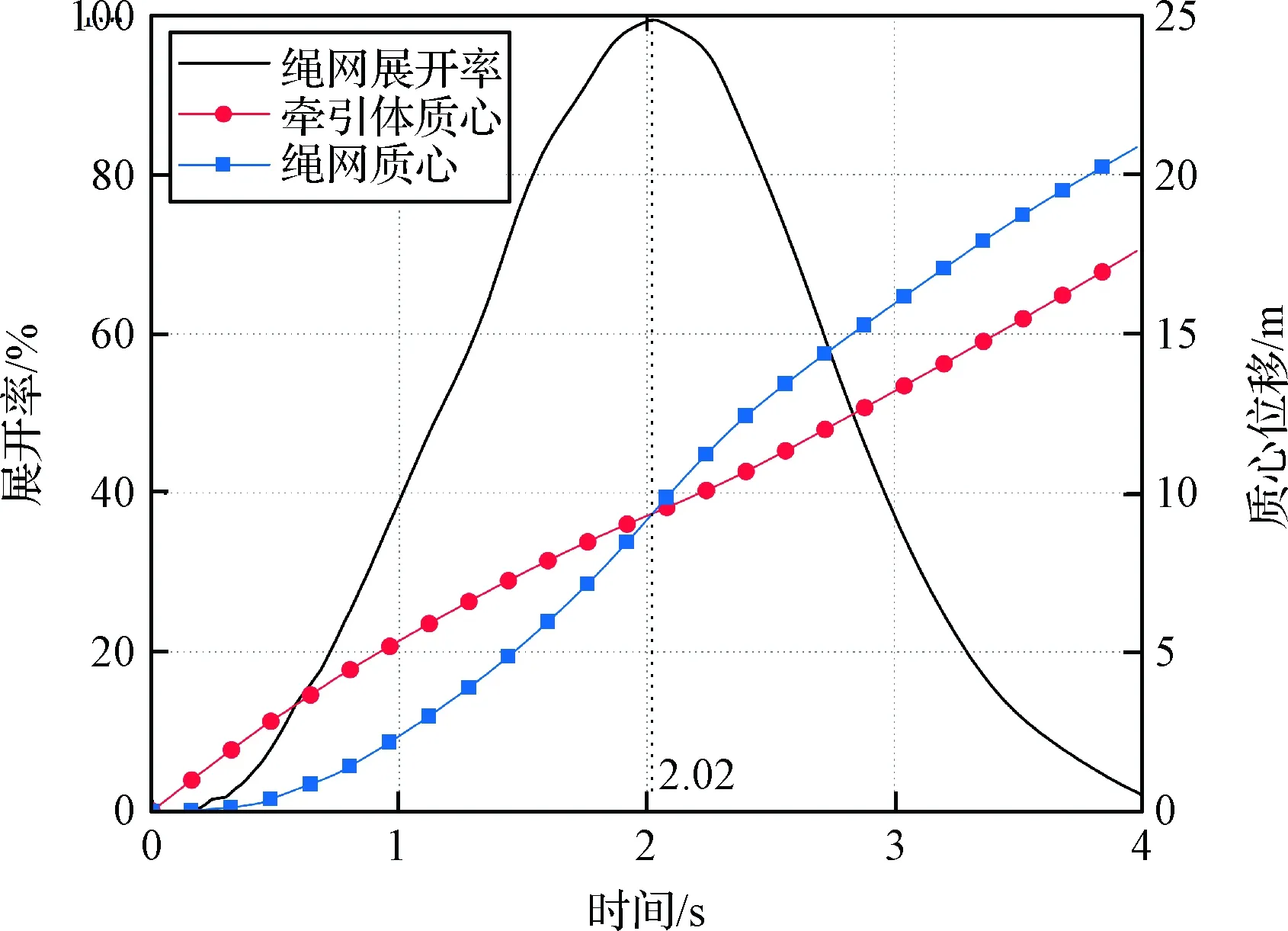
图1 质心追逐过程Fig.1 The chase of the center of masses
可以发现绳网展开率在约2.02 s时达到最大,之后由于回弹现象迅速下降。而0 s时刻由于绳网本体及牵引体位于同一平面,两者质心位移均为0。随着绳网的逐渐展开,两者的质心开始移动,由于牵引体具有较大初速度,其质心位移领先于绳网本体,但是通过图1可以发现,绳网质心的移动速度要大于牵引体质心。约2.02 s时,绳网质心与牵引体质心到达同一位置,并在后续过程中超过牵引体质心。因此绳网的回弹现象可以描述为绳网质心对牵引体质心的追逐过程,当绳网质心追上牵引体质心时,绳网位于最大展开率附近,此时绳网外形接近平面,无回弹发生。绳网质心的位移超越牵引体的质心时,绳网网面凸出开始回弹。
1.2 基于拖曳绳控制的绳网回弹抑制方法
为了抑制绳网回弹,可以通过降低绳网质心对牵引体质心的追逐速率实现。而完整的绳网系统都具有拖曳绳,用于绳网成功捕获后将目标脱离至坟墓轨道[19]。同时由于拖曳过程需要保持抓捕目标与拖曳船之间的安全距离,拖曳系统均具有绳系张力控制功能,可以控制拖曳绳对于绳网连接点的拉力。
本研究在不额外增加任何装置的前提下,通过拖曳系统中的绳系张力控制功能,在绳网展开的过程中对绳网中心的连接点施加持续控制力,从而降低绳网质心的追逐速度,抑制回弹现象,提高绳网的展开性能。有控展开示意图如图2所示,发射平台在绳网完全离开后,通过拖曳绳施加控制力Fcon,在Fcon的作用下绳网本体的速度降低,其质心Mn对牵引体质心Mb的追逐速率也相应降低,最终延缓两质心的相遇,抑制绳网回弹。由于绳索具有可拉不可压的特点,Fcon的方向始终朝向发射平台。控制力方向确定的情况下,如何确定拖曳绳控制力在控制区间内的大小是提高绳网展开性能的关键。

图2 有控展开示意图Fig.2 The deployment method with control
2 基于遗传算法的绳网控制力优化
2.1 绳网性能衡量指标
显然绳网的展开率越大,成功抓捕目标的概率越高,因此根据展开面积的变化规律,衡量绳网展开性能的衡量指标可以细化为以下5个参数(如图3所示):
1)最大展开率:绳网展开的最大面积与绳网设计面积的比值。
2)展开时间:指绳网展开到最大展开率的时间。
3)展开位移:指绳网展开到最大展开率的位移。
4)有效展开时间:绳网展开率超过设定阈值的持续时间。
5)有效展开位移:绳网展开率超过设定阈值的飞行距离,一般采用80%作为阈值[9,13,16]。
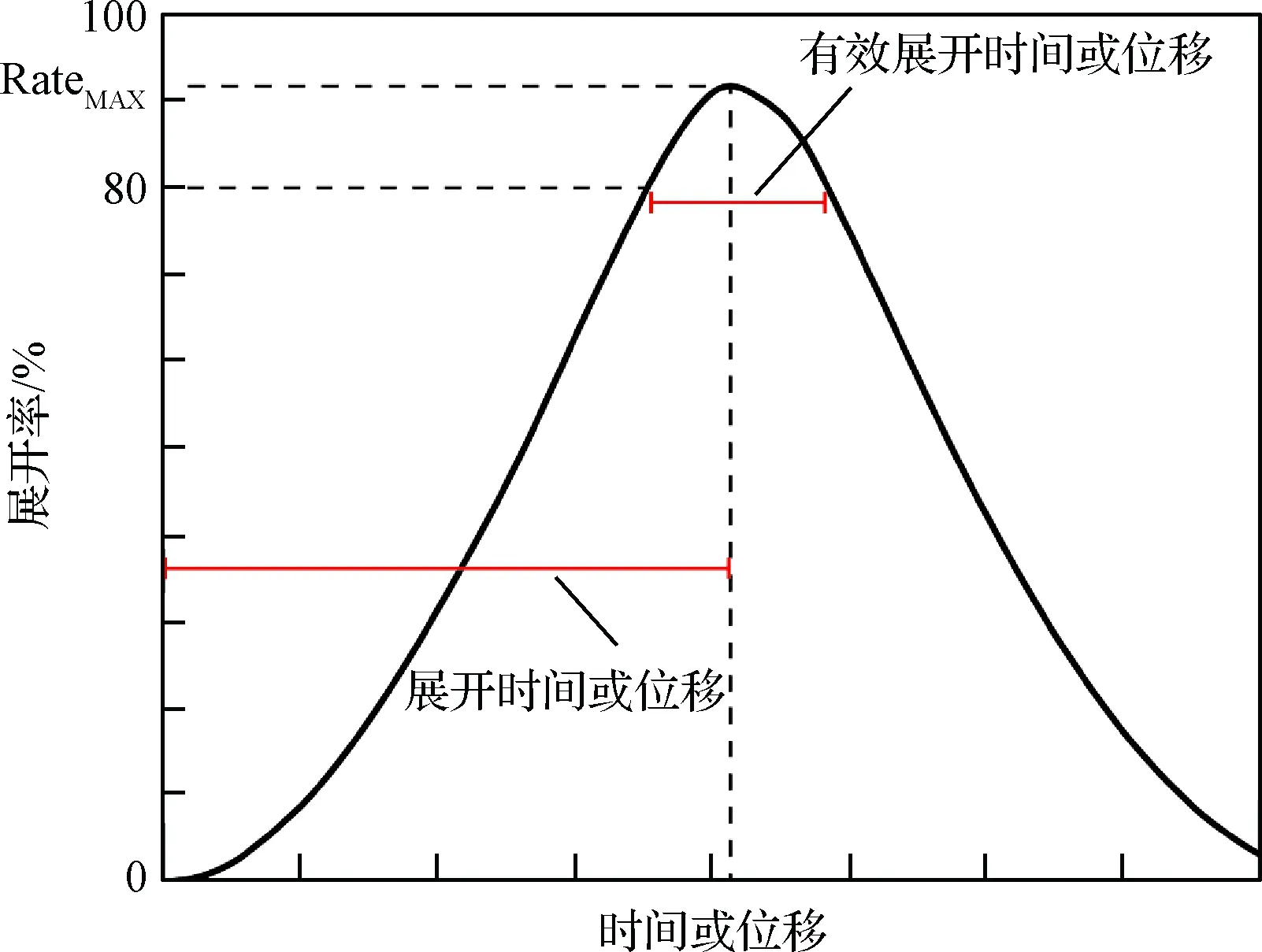
图3 展开性能指标Fig.3 Performance criteria of deployment
展开时间和展开位移可以为最佳抓捕时机的确定提供依据,这两个指标可以通过发射速率和发射角度进行调整。尽管展开率越大,抓捕成功的几率越高,但是通常认为只要展开率超过设定的阈值,抓捕任务便可以完成。并且展开率超过设定阈值后,绳网飞行的距离越远,其有效抓捕区间覆盖的距离越大,抓捕目标的成功率越高。因此有效展开位移可以作为衡量绳网抓捕成功率的指标。相比有效展开位移,有效展开时间只能说明绳网展开率超过阈值的时间,对于抓捕成功评估意义不大。同时,由于已经设定了展开率阈值,绳网最大展开率的大小在本文中不做重点讨论。
综上所述,较大的有效展开位移表示绳网抓捕区间覆盖范围较大,能够提高抓捕成功率。所以选择有效展开位移de作为本研究的优化目标,并使用80%作为本研究的阈值。
2.2 控制力曲线优化
空间绳网的展开是一个非线性的动力学过程,拖曳绳对绳网的控制力需要随时间而变化才可能使得绳网展开性能得到提高。因此可以将绳网性能优化问题细化为绳网最优控制力曲线优化问题。如果将每一时刻的控制力大小作为优化对象,显然可以得到最佳的有效展开位移优化结果。但是相邻时刻的控制力大小波动较大,将影响控制系统对于控制力曲线的跟踪精度,增加张力控制系统的负担。

图4 控制状态序列示意图Fig.4 The sequence of control state
遗传算法是一种模拟生物进化机制的全局优化算法,不需考虑所优化问题的内在工作原理,可以处理定义在离散、连续或混合搜索空间上的线性或非线性目标函数[20-21]。本研究设置3个增大档位和3个减小档位,即|p|=|q|=3,并使用整数编码对包含保持档在内的7个档位进行编码。各个档位对应的控制力变化率和编码值如表1所示。

表1 控制力变化率档位编码Table 1 Code of control gear
通过优化控制力曲线,使得绳网的有效展开位移de最大化。控制力的初始值应为0,考虑到在实际工况中绳网与目标的碰撞接触发生在结束施加控制力之前,因此不对控制结束时刻的控制力进行约束,在控制结束后将控制力归零。由于绳索“可拉不可压”的特性,拖曳绳只能对绳网施加朝向平台的拉力。若将朝向平台的拉力方向设定为正,则整个控制阶段绳网的所受拉力均为非负值。综上,绳网的控制力曲线优化问题可以描述为:
(1)
其中,tst为控制区间的开始时间,tend为结束时间。
在已知控制状态序列时,可以反推出任意时刻控制力的大小。若t时刻时处于第i个控制状态区间,则此时刻的控制力可以表示为:
(2)
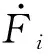
3 绳网动力学模型
使用弹簧质点模型对绳网进行建模的基本原理是将绳网离散为有质量的质点和质点间无质量的弹簧、阻尼器单元。计算各质点的受力并建立相应的动力学方程,最后通过联立各个质点的动力学方程得到绳网的位移及受力情况。
本研究对网格为正方形的四边形绳网进行研究,绳网网角依次连接四个牵引体。将绳网物理节点视为集中质量,绳段视为弹簧和阻尼器并联的无质量单元,绳网的构型及离散方法如图1所示。

图5 绳网构型Fig.5 Configuration of the tether-net
根据牛顿第二定律,质点i的动力学方程为:
(3)
其中,mi为质点i的等效质量,根据质点在绳网内的位置分布有如下定义:
(4)

Fext,i=Fcon·eL
(5)
其中,eL是指向发射平台的单位向量。Fint,i是相邻绳段传递给质点的内力,表示如下:
(6)
当绳段端点距离大于绳段原始长度时,绳段中产生拉力,当绳段端点距离小于绳段原始长度时绳段内不产生拉力。因此在以i,j为端点的绳段中,i点所受张力如下式:
(7)
式中:kij是网绳的等效刚度系数:
kij=EA/l0
(8)
式中:E是绳网选用材料的杨氏模量,A是网绳的横截面积,lij是绳段的真实长度,l0是绳段的原始长度。eij是从i指向j的单位向量,vij是质点i与质点j的相对速度。dij是阻尼系数:
(9)
式中:ζ为绳网选用材料的阻尼比。
4 仿真结果及讨论
4.1 恒定控制力
首先通过数值仿真研究绳网控制力Fcon为恒力的情况。建立三维笛卡尔坐标系,将绳网收纳放置在坐标系原点处,绳网的飞行方向为z轴正向。牵引体的发射速率vb=7 m·s-1,发射角度θb=30°,其中θb是牵引体的发射方向与绳网飞行方向(z轴)的夹角。同时本文算例在理想空间环境中进行,不考虑引力、摄动及空气阻力,所研究绳网的参数如表2所示。

表2 绳网参数Table 2 Simulation parameters
基于上述输入参数,无控制力时绳网在约1.08 s时能够完全离开发射平台,在约2.47 s时展开率能够第二次达到80%的阈值,如图8所示。为了统一展开性能的衡量标准,本研究中的控制力施加时间均设置为1.1~2.5 s。同时,本研究使用Matlab编写绳网仿真程序,所有算例的仿真时长均设置4 s。设置一系列恒定控制力水平如表3所示。并对不同控制力下的绳网展开过程进行仿真。

表3 恒定控制力列表Table 3 List of constant forces
图6给出了控制力为恒力时绳网面展开率随位移的变化曲线。表4给出了相比无控工况,不同控制力下绳网有效展开位移的提升率。可以发现,当控制力为恒力时,随着控制的增大,绳网的有效位移得到少量提升。当控制力为0.5 N时有效位移的提升率最高,为9.52%。若控制力继续增加,则提升效果显著下降。当控制力大于2 N时,绳网的整个展开阶段均无法到达80%的设定阈值。值得注意的是,控制力的施加会降低绳网系统的总动能,因此施加控制力后绳网的最大展开率低于无控工况。综上可知,仅仅通过拖曳绳对绳网施加恒定的控制力对绳网有效展开位移的提升有限,因此有必要通过调节控制区间内每一时刻的控制力大小使得绳网的展开性能进一步提升。
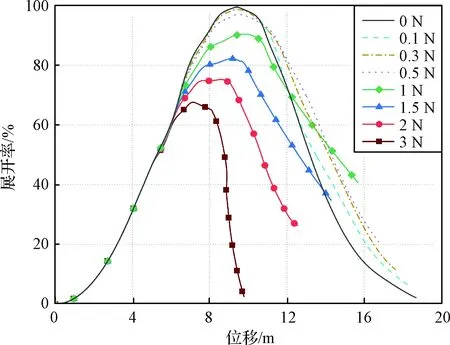
图6 展开率随位移变化曲线Fig.6 Comparison of deployment simulation results with constant force
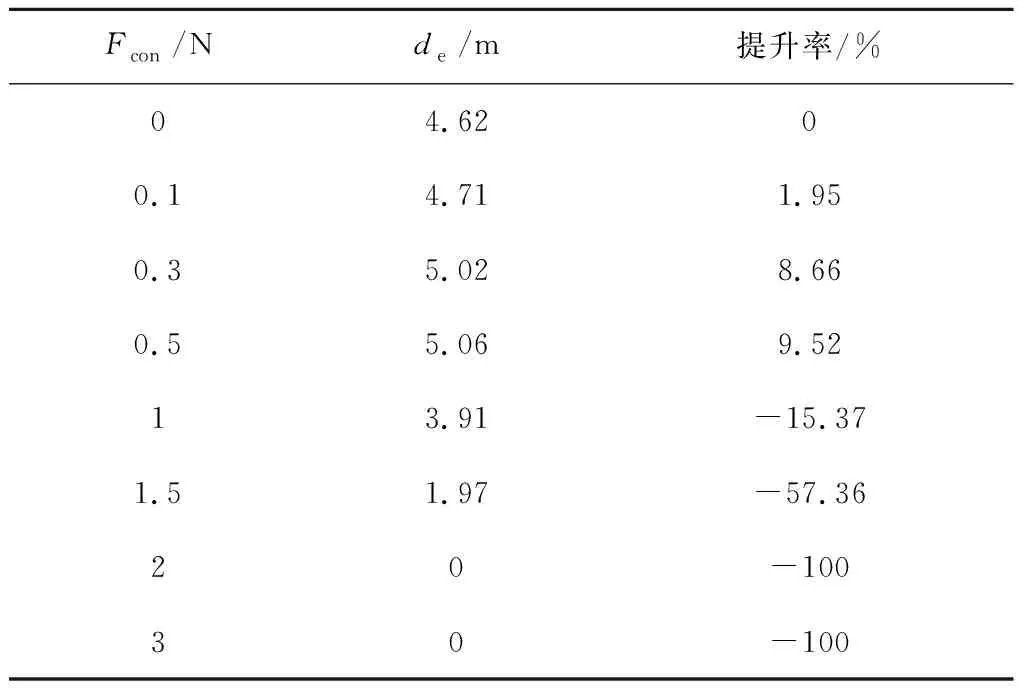
表4 有效展开位移提升率Table 4 The increase of the effective displacement
4.2 变控制力
为了进一步提升有控状态下绳网的展开性能,使用经过遗传算法优化的控制力曲线进行研究。本节使用的绳网参数和发射参数与4.1节相同。使用Matlab编写了采用整数编码的遗传算法,初始种群规模为40,进化代数为100。控制区间为1.1~2.5 s,并将此区间离散为10段,控制力档位及编码值如表1所示。优化后的控制力档位序列及对应的控制力变化率见表5。

表5 优化后的档位序列Table 5 Optimized sequence of control gear
优化后的控制力曲线及对应档位如图7所示。可以发现,优化后的控制力呈现“增-减-增”的变化趋势。最大控制力出现在1.38~1.52 s处,大小为1.68 N。最小控制力出现在2.22 s处,大小为0 N。

图7 优化后的控制力曲线及档位Fig.7 Optimized control force and control gear
绳网的展开率随时间、位移的变化曲线分别如图8和图9所示。无控绳网的展开率在1.54 s时首次达到80%,此时对应的飞行位移为6.93 m。在2.47 s时无控绳网的展开率第二次达到80%,之后迅速下降,此时对应的飞行位移为11.55 m,无控绳网的有效展开位移为4.62 m。有控绳网的展开率分别在1.68 s和3.35 s处到80%,对应的飞行位移分别为7.55 m和14.21 m。可知有控绳网的有效展开位移为6.66 m,相比无控绳网提升了约44.16%。由于控制力的作用,有控绳网的动能相比无控绳网有所下降,其最大展开率低于无控绳网。
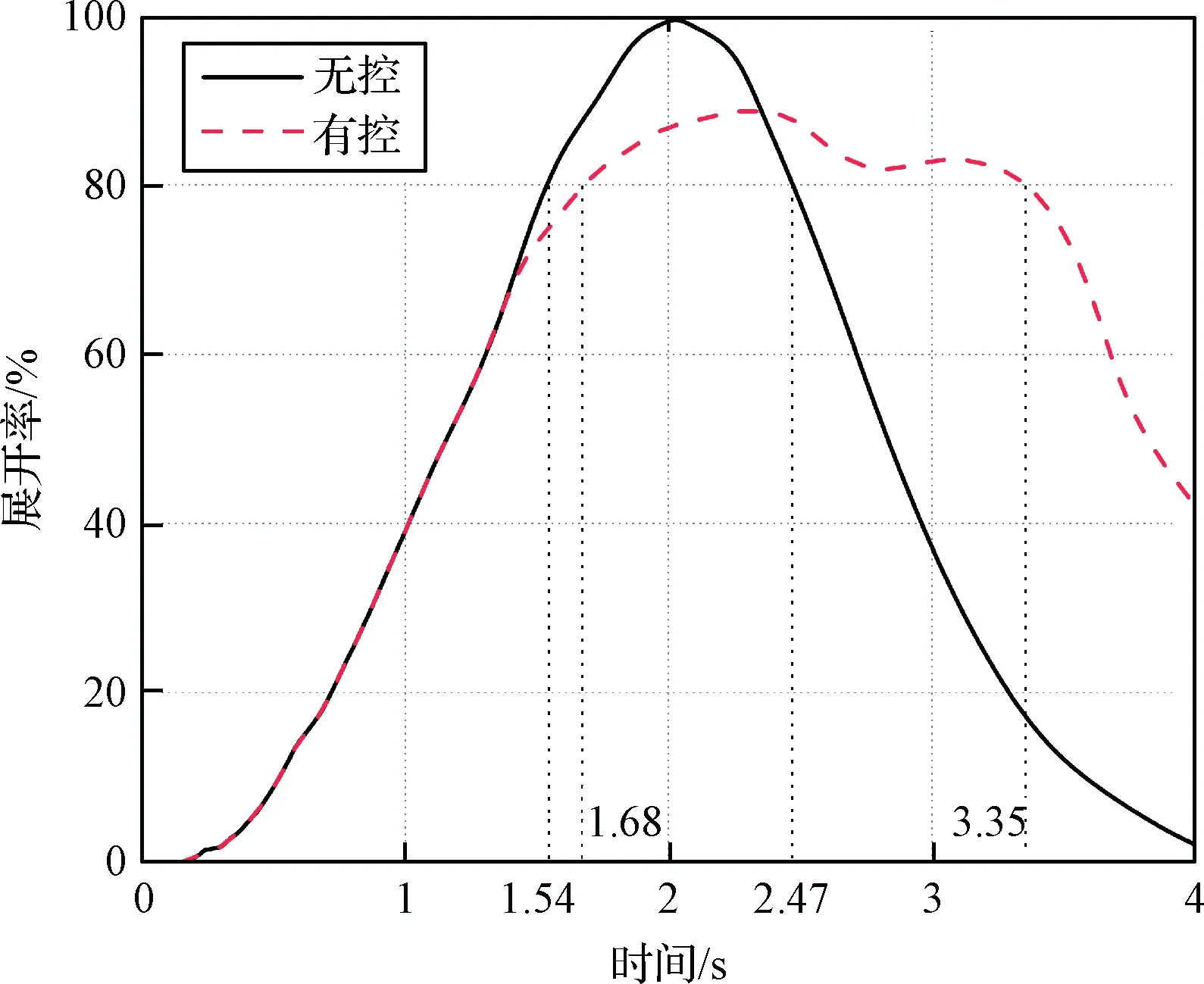
图8 展开率的时间历程Fig.8 Time history of deployment rate with and without control
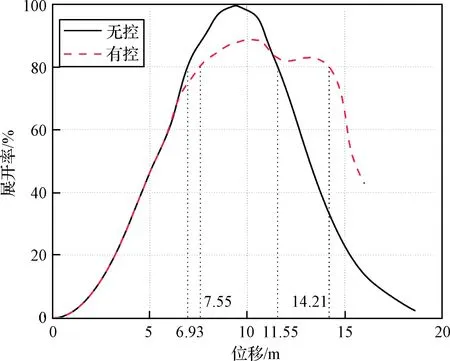
图9 展开率随位移变化Fig.9 Displacement history of deployment rate with and without control
图10中,进一步绘制了无控绳网展开率第一次、第二次达到80%时,以及有控绳网展开率第二次达到80%时,无控、有控下绳网的网形图。1.54 s时无控绳网的展开率首次达到80%,此时无控、有控两种工况下绳网的形态及展开率均较为接近。由于控制力的作用,有控绳网的底部呈现凸起。2.47 s时无控绳网的展开率第二次达到80%,此时有控绳网的展开率高于无控绳网,约为87%。此时无控绳网的网体已经在z轴正向超越了牵引体,并出现了明显的回弹现象。而有控绳网上表面的网形较为平整,由于控制力的作用绳网中心在z轴负向出现了较为明显的下凹。3.35 s时有控绳网展开率第二次达到80%,此时有控绳网出现了回弹现象,但是其展开率依旧满足抓捕需求。而此时无控绳网的展开率已经不足20%,其网体部分也出现了穿透和缠绕现象,无法进行有效抓捕。通过上述分析可知,展开过程中,有控绳网在网形保持、有效展开位移等性能指标上均优于无控绳网。
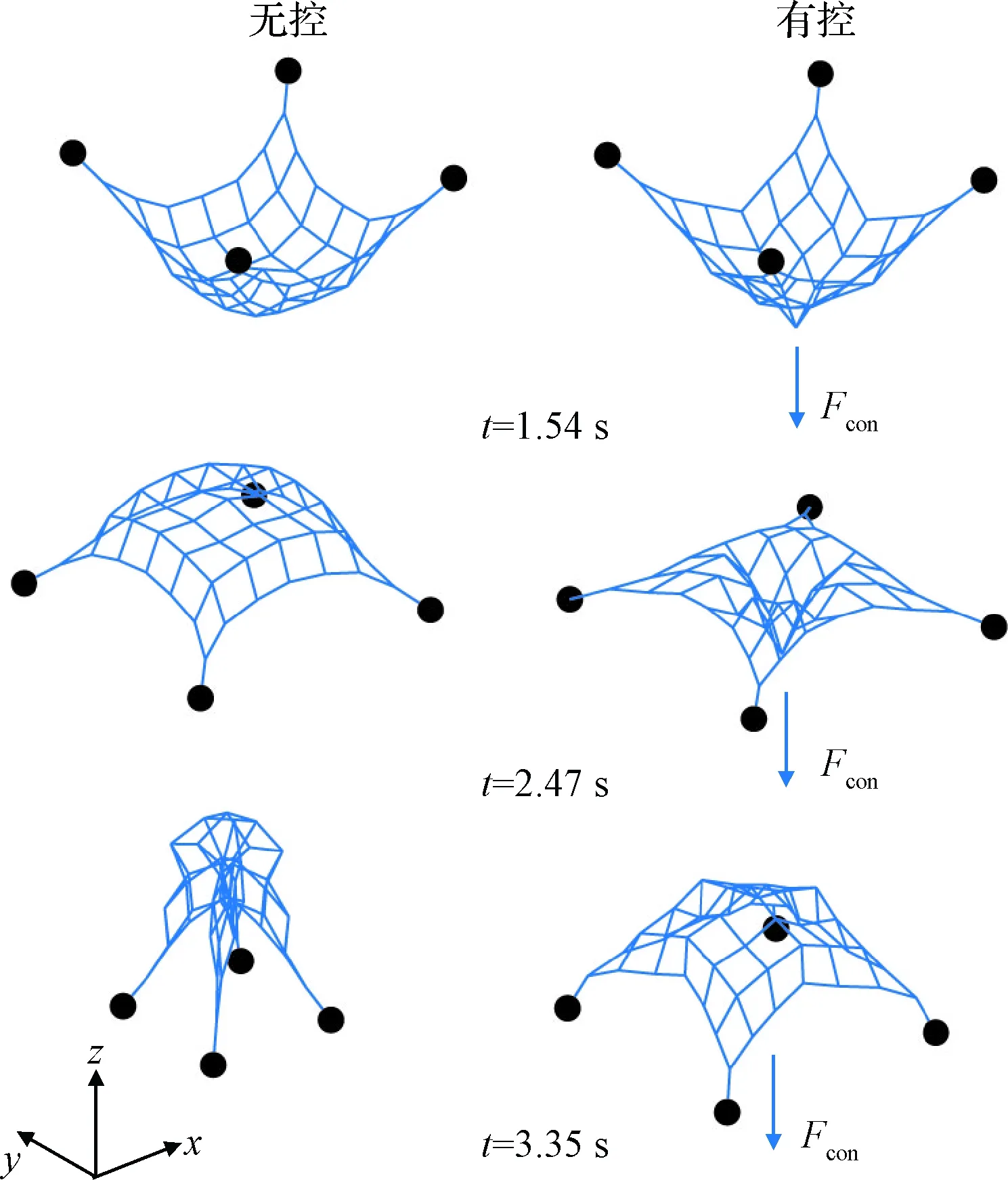
图10 网形对比Fig.10 Deployment sequence with and without control
分别绘制了绳网和牵引体的质心位移随时间的变化曲线,如图11所示。可以发现,无论是否施加控制力,绳网质心对牵引体质心都存在追逐趋势,并最终超越牵引体质心。无控工况中,两质心在约2.02 s时相遇,此时的位移为9.33 m。施加控制力后,两质心在约2.2 s处相遇,位移为9.62 m。控制力推迟了质点的相遇时间,使得质心交点延迟出现了0.18 s,并使得相交时的位移延长了0.29 m。

图11 质心位移对比Fig.11 Displacement of the centers of masses
图12分别给出了绳网和牵引体的质心追逐速率。无控工况中,由于需要牵拉绳网,牵引体质心的速率首先呈现下降趋势,而绳网质心的速率逐渐上升。在约2 s时绳网质心达到最大速率约为0.178 m·s-1,牵引体质心达到最小速率约为0.065 m·s-1。此时绳网的展开率接近最大值,并开始出现回弹现象。之后绳网质心的速率逐渐下降,而牵引体质心的速率逐渐上升。这也说明了使用质心追逐描述绳网回弹现象的正确性。有控工况中质心速率的变化趋势与无控工况类似。但是,开始施加控制力后,相比无控工况,有控工况下两质心的速率均出现了显著下降。并且在控制区间内,绳网质心速率的下降幅度要大于牵引体质心速率的下降幅度。这说明控制力成功推迟了两质心相遇的时间,抑制了回弹现象,最终提高了绳网的展开性能。
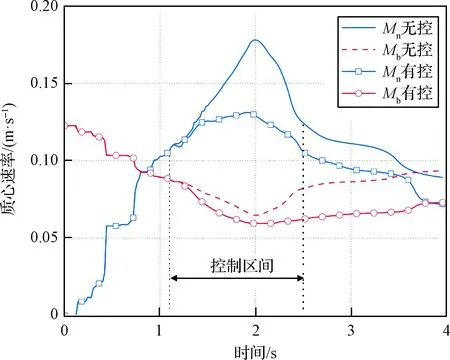
图12 质心追逐速率Fig.12 Velocity of the center of masses
5 结 论
针对绳网的回弹现象提出了一种基于拖曳绳张力控制的绳网展开控制方法。使用绳网和牵引体的质心描述绳网展开过程中的回弹现象,将抑制绳网回弹转化为抑制绳网对牵引体的质心追逐。由此提出通过拖曳绳对展开过程中的绳网施加控制力,降低绳网质心对牵引体质心的追逐速率,以提高绳网的展开性能。以控制力变化率为优化对象,以绳网有效展开位移为优化目标,提出了一种基于遗传算法的控制力曲线优化策略。基于弹簧质点法建立了绳网的动力学模型,并通过数值仿真对比了无控、恒力和变力控制下绳网的展开性能。通过研究得出以下结论:
1)提出的质心追逐可以较好地描述绳网的回弹现象,为后续绳网高性能展开方法的提出提供思路。
2)仅施加恒定控制力难以有效提高绳网的展开性能,提出的控制力优化策略可以成功优化出所需控制力曲线。
3)提出的有控展开方法可以有效抑制绳网的回弹现象,相比无控工况可以将绳网有效展开位移提高约44.16%,但最大展开率会有所下降。

