基于特征空间变换的运载火箭Pogo模型降阶方法

谭述君，高 强，赵 旺，刘锦凡

(1.大连理工大学工业装备结构分析国家重点实验室，大连 116024；2.大连理工大学辽宁省空天飞行器前沿技术重点实验室，大连 116024；3.上海宇航系统工程研究所，上海 201108)

0 引 言

Pogo是大型液体运载火箭在飞行过程中由推进系统液路脉动与结构振动相互耦合而产生的一种自激振动现象[1]。Pogo会导致运载火箭结构破坏、影响飞行稳定性，甚至威胁到航天员的生命等[2-4]，而且Pogo在不同型号火箭、同一型号火箭的不同任务飞行中都曾出现过，具有任务依赖性，发生机理复杂[5]。因此，开展Pogo建模方法研究对揭示Pogo发生机理和抑制Pogo振动具有重要意义。

国内外学者对运载火箭Pogo建模开展了大量研究，其中传递矩阵法和闭环传递函数法因其简洁得到了广泛应用[6-9]，然而这些方法难以处理捆绑火箭的助推与芯级耦合、多模态耦合、多作用力耦合等问题[3]。王建民等[10]提出对捆绑火箭的Pogo问题必须基于空间模态进行设计。Oppenheim与Rubin[11]面向工程中的复杂液路系统提出了一种基于有限元描述的状态方程法，可以推广到复杂三维管路的建模，已成功应用于中国CZ-2F火箭Pogo问题的研究[3]。在此基础上，Tan等[12]和Wang等[13]基于独立流量位移提出改进的状态方程法，解决了Rubin方法的奇异性问题。文献[14-15]则通过对阻抗函数矩阵进行有理多项式逼近，提出了快速求解Pogo振动特征值和稳定性分析的方法。牛泽雄等[16]采用分段三次Hermite插值得到了管路系统描述的新形式。Park等[17]改进了结构振动的三维和一维单元混合的有限元建模方法以更精确地进行Pogo分析和预测。赵治华[18]则提出了Pogo振动的多体动力学建模方法，分析了包含结构纵横扭模态的液体火箭Pogo振动稳定性。上述建模方法更真实地描述了Pogo特性，同时也导致状态空间模型的维数过高和奇异性问题。对此，王庆伟等[19]提出了一种Pogo模型缩聚方法，通过对液体输送管路的局部降阶实现对整体Pogo模型的降阶，验证了降阶的正确性和可行性。然而该方法仅限于对液体输送管路的降阶，不能处理众多推进系统部件、支路连接产生的高维问题。因此，需要进一步发展适用于不同型号推进系统的运载火箭Pogo模型的一般性方法。

本文基于特征空间变换理论提出了一种面向运载火箭Pogo状态空间模型的整体降阶方法。该方法具有很好的通用性，并通过对两种不同型号推进系统的运载火箭Pogo问题的分析和仿真，校验了所提出的降阶方法的正确性和通用性。

1 Pogo状态空间模型

运载火箭的Pogo振动方程由结构系统的振动方程和推进系统的脉动方程相互耦合生成，其中推进系统由众多不同特性的物理部件组成，动力学方程复杂，因此推进系统脉动方程的建立是其关键。Oppenheim等[11]提出的状态方程法采用了有限元描述推进系统各物理部件的系统方程，可以严格处理流体容器的任意运动以及作用于结构系统的所有力，从而建立了一套系统的分析方法。对于典型的运载火箭推进系统所包含的贮箱、燃料输送管路、蓄压器、泵、推力室等物理部件，该方法的优点是可将任一部件统一描述为不超过二阶微分的动力学方程。

以可压缩直管为例[11]，如果将管路划分为Nd段，只要每段管路单元的长度ld满足

(1)

式中：a为液路压力传播的有效声速，fu是系统分析所关心的最高频率,那么每一段的动力学方程可表示为

(2)

(3)

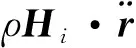
对于结构系统，采用二阶微分的模态振动方程来描述。如第n阶模态振动方程为

(4)

式中：qn为结构振动的模态位移，Mn，ωn和ξn分别为第n阶模态质量、模态频率和模态阻尼比，fi是第i个推进系统单元作用于结构的力向量，φin则为第i个推进系统单元处的结构第n阶模态阵型向量，右端项体现了推进系统对结构振动的影响。

由于结构系统和推进系统各部件的动力学方程都是不超过二阶微分的动力学方程，因此引入状态变量v，包括推进系统的脉动重量位移w=[…,wi, …]T和脉动压力p=[…,pi, …]T，以及结构系统的模态位移q=[…,qn, …]T，那么结构系统和推进系统耦合的Pogo方程可以写成标准的二阶微分矩阵方程形式[11]，

(5)

(6)

其中,

(7)

基于状态空间方程式，通过求解广义特征值问题,可以进行Pogo稳定性分析。针对式(6)中E矩阵奇异的问题，文献[12-13]提出了改进方法，导出了式(6)形式的Pogo非奇异状态空间方程，可同时用于时域仿真和稳定性分析。

2 Pogo模型的降阶方法

状态方程法为Pogo分析提供了一套系统方法，在实际工程中得到了成功的应用。然而，正如式(1)所述，为了提高Pogo分析的精度，需要将输送管路划分为更多的段数，这将导致状态方程式(6)的维数更高，增加计算困难。另一方面，文献[12-13]解决了液路推进系统状态空间模型的奇异性问题，但对于含气路推进系统的Pogo建模，仍然存在奇异问题。这给时域仿真和控制系统设计带来了极大困难。因此，本节给出Pogo状态空间模型的降阶方法。

不失一般性，将建立的Pogo状态空间方程描述为

(8)

式中：E和A是系统矩阵，f是外部干扰或控制力。对矩阵E的奇异性不做要求。

定理1. 矩阵(E,A)和矩阵(ET,AT)具有相同的广义特征值。

证.设λ是矩阵(E,A)的广义特征值，那么广义特征值矩阵(λE-A)的行列式为零，又因为其转置矩阵具有相同的行列式[20]，即

0=|λE-A|=|(λE-A)T|=|λET-AT|

(9)

所以λ也是矩阵(ET,AT)的广义特征值。即矩阵(E,A)和矩阵(ET,AT)具有相同的广义特征值。证毕。

证. 设λi和λj分别是矩阵(E,A)的第i阶和第j阶广义特征值，根据定理1，λi和λj也是矩阵(ET,AT)的广义特征值。因为λi是矩阵(E,A)的广义特征值，所以存在对应的特征向量φi满足

λiEφi=Aφi

(10)

因为λj是矩阵(ET,AT)的广义特征值，所以存在对应的特征向量φt,j满足

λjETφt,j=ATφt,j

(11)

将式(11)两边转置，并同时右乘向量φi，得到

(12)

将式(10)代入式(12)，整理得到

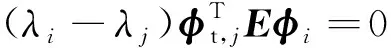
(13)

因为矩阵(E,A)是Pogo状态空间方程的系统矩阵，每一个特征值对应系统的某一阶模态，包括结构振动模态与推进系统的液路脉动模态，所以各阶特征值不同，故当i≠j时，λi≠λj。因此由式(13)可以导出

(14)

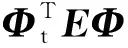
接下来，本节将基于上述定理，通过特征空间变换理论进行Pogo状态空间方程(8)的降阶研究。

对Pogo状态空间方程的系统矩阵(E,A)进行广义特征值分析，即

EΦΛ=AΦ

(15)

式中：Λ和Φ分别是对角的特征值矩阵和特征向量矩阵。将Λ按特征值的模从小到大排列，特征向量Φ也对应地排列，如下所示

Λ=diag(λ1，λ2，…，λN)

(16)

(17)

式中：λ1,λ2,…,λN是特征值，且|λ1|≤|λ2|≤…≤|λN|。

对矩阵(ET,AT)进行广义特征值分析。由定理1可知，式(15)和式(16)中的Λ也是矩阵(ET,AT)的广义特征值，即

ETΦtΛ=ATΦt

(18)

式中：特征向量矩阵Φt也按式(16)中的特征值对应排列，如下所示

Φt=[φt,1, φt,2, …, φt,N]

(19)

利用特征向量矩阵Φ对Pogo状态空间方程式(8)的原状态变量x进行变换如下

x=Φη

(20)

将式(20)代入式(8)，得到

(21)

将式(15)代入式(21)，得到

(22)

(23)

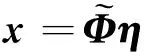
(24)

(25)

(26)

式(26)就是用状态η描述的非奇异Pogo降阶模型，解决了原Pogo模型的奇异性和维数高的问题，可以方便地开展时域仿真、控制系统设计等工作。求解得到η之后，利用变换式(24)可以求得原状态x的解。

几点说明：

1)一般来说，振动系统的响应通过截断少数低阶特征值及其特征向量就可以实现高精度的近似，因此对于降阶模型，感兴趣的特征值通常取式(16)中的低阶特征值。

2)即使矩阵E是奇异的，选取前面低阶特征值及其特征向量导出的降阶系统(26)也是非奇异的。因此该方法也可以实现原状态方程式(8)的去奇异化处理。

3)η初值η(t0)的确定。基于状态微分方程(26)求解η(t)时，需要确定初值η(t0)。因为原状态初值x(t0)已知，因此可以根据变换(24)的反变换式得到

(27)

4)运算过程的实数化。由于E和A是非对称实矩阵，因此特征值Λ和特征向量矩阵Φ可能是复数，而如果是复数则必然是复共轭成对出现的[20]，与结构系统或推进系统的二阶振动方程相对应。因此矩阵的特征值和特征向量可以描述为

(28)

Φ=[Φr+iΦi,Φr-iΦi]

(29)

式中：Λr和Λi分别是特征值Λ的实部和虚部，Φr和Φi分别是特征向量矩阵Φ的实部和虚部。

将式(28)和式(29)代入式(15)，分离实部和虚部，得到

(30)

因此，前述方法中的特征值和特征向量可以用下面实数矩阵描述，即

(31)

3 仿真算例

本节分别利用液路推进系统的气-液路耦合推进系统的两种不同型号火箭的Pogo分析与仿真，来校验本文降阶方法和去奇异化方法的正确性。需要说明的是，在不影响对比验证的前提下，根据保密要求，本文对仿真结果的数据进行了适当归一化处理。

算例1：液路推进系统的某型号火箭

某型号火箭采用液氢-液氧发动机，推进系统完全由液体输送管路连接构成，结构系统采用两阶纵向模态振动方程。对此，可采用文献[12-13]提出的改进的Rubin状态空间建模方法，得到式(8)所示的Pogo非奇异状态空间模型，直接应用于时域仿真。然而，由于输送管路需要划分很多段数，导出的状态空间模型维数高达45阶(如果采用原Rubin方法建模[11]，导出的状态空间模型奇异，且维数增加近一倍)。

图1 预压泵入口随机脉动干扰Fig.1 Random perturbation at the inlet of prepressure pump

图2和图3分别给出了随机脉动干扰下的结构模态位移和推力室脉动压力的响应曲线。图4给出了降阶模型与原模型仿真响应相对误差曲线。可以看出相对误差小于10-1量级，大部分在10-2量级。相对于求解器精度10-3来说，降阶模型的维数虽然仅为原模型的1/4，但是仿真结果与原模型高度吻合，校验了降阶模型的正确性。这也说明降阶模型保留了原模型的主要特性，由于管路划分产生的高阶模态是非主要模态，是可以忽略的，从而为Pogo主动抑制设计提供了更合适的控制系统模型。

图2 结构模态位移Fig.2 Modal displacements of structure systems

图3 推力室脉动压力Fig.3 Perturbed pressures of the chamber

图4 降阶模型与原模型仿真响应相对误差Fig.4 Relative errors between the reduced model and the original model

表1进一步给出了MATLAB的ode45(·)函数在不同求解精度下，采用降阶模型和原模型仿真耗费的时间(程序在Intel(R) Core(TM) i7-8550U CPU处理器的笔记本电脑上运行)。表1中数据显示当求解精度较低时(10-3)，利用降阶模型仿真的效率是原模型的14倍；当求解精度较高时(10-6)，利用降阶模型仿真的效率是原模型的50倍。因此，利用降阶模型仿真的计算效率大大提高，提高了一个数量级以上。从表1还可以看出，当求解精度从10-3提高到10-6时，原模型由于维数较高(其中含有大量不起主要作用的高阶模态)，计算时间增加了298%；而降阶模型由于显著降低了维数，计算时间仅增加了11%，计算效率优势更为明显。

表1 降阶模型和原模型仿真的计算时间Table 1 Computational time for the reduced model and the original model

算例2：气-液路耦合推进系统的某型号火箭

某型号火箭采用新型液氧-煤油富氧补燃循环发动机推进系统[21]，除了传统的液路还包含补燃的气路，属于气-液路耦合的推进系统，结构系统取两阶纵向模态振动方程。由于气路的存在，导出的如式(8)所示Pogo状态空间模型是奇异的，维数是60阶。基于该状态空间模型进行稳定性分析，图5给出了利用该模型分析得到的不同秒点的Pogo系统结构阻尼比。可以看出该Pogo系统在0.2时间点附近第一阶结构阻尼比小于零，振动失稳。

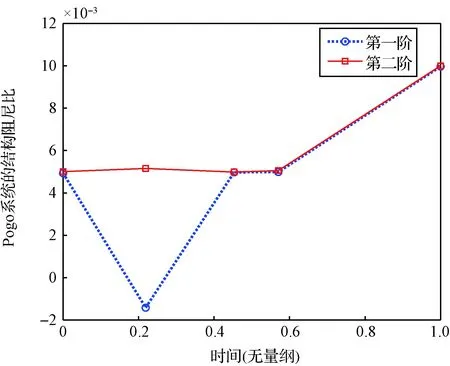
图5 Pogo系统的结构阻尼比Fig.5 Structural damp ratios of the Pogo system

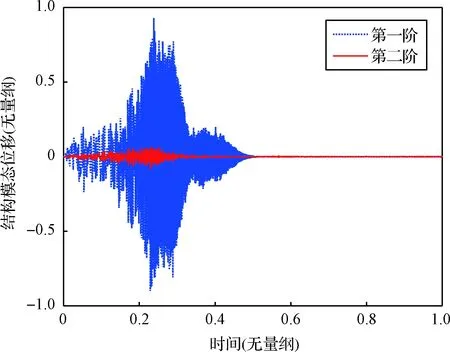
图6 结构模态位移Fig.6 Modal displacements of structure systems

图7 推力室脉动压力Fig.7 Perturbed pressures of the chamber

图6给出了Pogo系统的结构模态位移响应曲线，从中可以看出结构第一阶模态位移在0.2时间点附近的区段明显发散，随后收敛，这与图5中的结构第一阶阻尼比曲线是一致的。同时结构第二阶模态位移在该时间段也出现一定程度的发散，而图5中结构第二阶阻尼比一直大于零，说明结构第二阶模态虽然并未失稳，但由于结构第一阶模态位移发散引起激励项的显著增大，从而导致第二阶模态位移响应也出现发散。图7给出了推力室脉动压力响应，可以看出推力室脉动压力尚未出现明显的发散情况。从上面的分析来看，采用降阶模型的仿真结果是合理的，校验了降阶方法的正确性。同时，也说明时域仿真与稳定性分析相结合可以更好地揭示Pogo特征和机理。

4 结 论

状态方程法是当前运载火箭Pogo振动研究中非常有优势的一种方法，同时也存在系统维数过高、存在奇异性等问题。本文采用特征空间变换理论开展了Pogo状态空间模型降阶方法的研究，并在两种不同类型推进系统的火箭Pogo问题中进行了仿真验证。研究结果表明，本文所提的降阶方法具有一般性，对奇异、非奇异Pogo状态空间模型都能得到正确的降阶模型，而且降阶效果明显，显著提高了计算效率。同时，研究显示基于降阶模型可以方便地进行Pogo时域仿真，而时域仿真结果能为Pogo特征描述和机理揭示提供重要的信息。进一步，降阶模型也更有利于Pogo主动抑制器的设计，为正引起关注的Pogo主动抑制研究[22]打下良好的基础。