ARIMA乘积季节模型在西藏自治区包虫病月发病人数中的预测应用

苑斌 石晓峰 霍春青 赵晶 何世华 赵玉华 严静 费雯 栾晓婷 金海强 孙永安

1菏泽医学专科学校附属医院神经内科，山东274000；2菏泽医学专科学校教务处，山东274000；3西藏自治区人民医院神经内科，拉萨850000；4清华大学附属第一医院神经内科，北京100016；5北京大学第一医院神经内科100034

棘球蚴病是人感染细粒棘球绦虫及多房棘球绦虫的幼虫（包虫囊）所致的全球畜牧业发达地区常见的人畜共患病，其又称为“包虫病”。在中国，包虫病的高发地集中于以畜牧业为主要产业的地区，比如西藏、新疆、内蒙古等地区。包虫囊主要是通过感染人的肝、肾、脑、肺等脏器，其发病病程长，严重影响患者身心健康，而且是高度致死的疾病，患者如不经及时治疗，10年内本病病死率为90%。因此掌握西藏高发地区流行趋势，是开展相关健康教育、预防治疗的前提和基础。本研究采用X-12自回归移动平均（X-12-ARIMA）乘积季节模型对西藏地区包虫病月报告病例数进行预测，从而为其防控提供参考依据。

1 资料与方法

1.1 资料来源包虫病患者的数据来源于西藏自治区人民医院。疾病分类标准则按照国际疾病ICD-10的分类，B67为包虫病的诊断编码。

1.2 方法

1.2.1 数据处理数据存储和管理则采用Microsoft Excel 2013、SAS 9.2对资料数据进行处理和统计分析。

1.2.2 X-12-ARIMA乘积季节模型X-12过程：X-12过程是根据美国人口普查局X-12-ARIMA季节调整程序改编，用于调整具有月度或季度时间序列数据。过程包含了X-11过程以及一些新的特征，一个主要提高是应用RegARIMA模型，利用该模型进行移动假日、月份长度、交易日效应等固定效应的调整。

标准：具有季节性的ARIMA模型为ARIMA（p，d，q）×（P，D，Q）S，其中p代表非季节性自回归阶数，d代表非季节性差分阶数，q代表差分阶数移动平均阶数，P代表季节性自回归阶数，D代表季节性差分阶数，Q代表季节性移动平均阶数以及S代表季节性周期。对于一个季节ARIMA模型来说：（1）确定周期，根据时序图进行判断；（2）判断时间序列是否平稳，根据时序图、自相关系数（ACF）和偏自相关系数（PACF）进行判断，如果得出非平稳时间序列，则进一步进行差分运算转化为平稳序列，并进行平稳性检验；（3）模型定阶，根据X-12模型基本原理、ACF以及PACF来进行模型定阶，所以拟合模型实质为ARIMA（p，q）×（P，Q），综合前面的d阶趋势差分和D阶以周期S为步长的季节差分运算，对原观察值序列拟合的乘积模型；（4）参数估计，使用条件最小二乘估计方法，确定该拟合模型的口径；（5）模型检验及预测应用，对拟合模型进行检验，并根据拟合模型对西藏地区2013至2018年包虫病月度发病率进行预测。

2 结 果

2.1 包虫病发病基本情况根据西藏自治区2013年8月至2018年7月包虫病月度发病人数数据显示，包虫病发病具有明显的季节效应和周期效应（表1）；其中可看出随着月份的增加包虫病发病率呈现逐渐下降的趋势，其发病高峰期为1月至4月。由此可看出西藏自治区包虫病月发病人数呈现波动性下降。

表1 2013至2018年西藏自治区包虫病月度发病人数（n）

2.2 模型识别季节调整和趋势成分分解（X-12）分析显示，西藏自治区2013至2018年包虫病月发病人数时间序列分解为趋势因素、季节因素和不规则因素。西藏自治区包虫病发病人数存在季节趋势，并先呈下降趋势，具有一定的周期性。

X-12的趋势成分分解分析中，在假定稳定性的前提下确定是否存在季节性检验，检验结果提示（F=11.41，P＜0.001）。结合原始数据序列、季节指数及季节性检验，提示包虫病月发病人数存在明显的高峰和低谷现象。

结合乘法模型在剔除季节和趋势成分后得到西藏自治区包虫病月发病人数的不规则成分影响程度大于1，则说明包虫病月发病人数受不规则成分影响较大。

2.3参数估计和模型诊断X-12模型中，根据序列图可看出2013至2018年包虫病月发病人数为不稳定的序列，存在波动性下降趋势。对于时序图，首先进行差分运算，再根据时序图的趋势进行1阶12步差分，差分后检验得出平稳序列。初步判断时间序列模型为ARIMA（p，1，q），采用IDENTIFY语句根据ACF和PACF以及AUTODML的自动选择过程，确定最终选择ARIMA（1，1，0）×（1，1，0）12模型为最佳模型，模型残差和参数检验见表2、表3、图1。

表2 不同延迟阶数残差的白噪声检验

表3 精确ARIMA最大似然估计

2.4 回代拟合及模型预测根据模型预测结果和拟合误差，即运用ARIMA（1，1，0）×（1，1，0）12模型进行回代拟合并对包虫病月发病人数进行预测，将序列拟合值和序列观察值联合作图，可以观察到拟合效果良好；并对2018至2019年包虫病月发病人数进行预测，并根据月发病人数可以得出西藏自治区包虫病月发病人数，见图2。

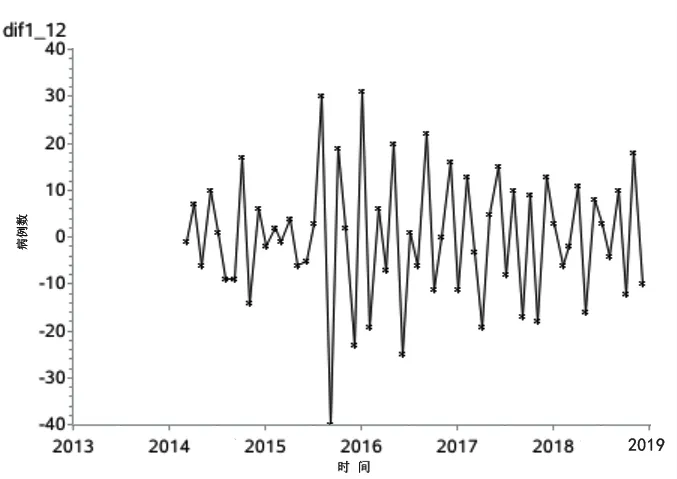
图1 2013至2018年西藏自治区包虫病月发病人数1阶12步差分后时序图

图2 2013至2019年包虫病月发病人数与预测发病人数拟合效果比较

3 讨 论

包虫病是一种人兽共患的由棘球属绦虫幼虫引起的寄生虫病，在畜牧发达地区存在高发病率、高病死率以及高复发率的特点，给当地居民造成严重的经济负担及健康问题［1］。并且中国是全世界包虫病发病最严重的国家之一［2］。在中国，青海、西藏、甘肃、宁夏等经济与医疗条件相对落后的地方，包虫病广泛流行。2016年西藏自治区对包虫病进行普查，发现该地区包虫病患病率为1.66%，全区包括7个地（市）的74个县（区）均有不同程度的流行［3］。狗、羊、牛是该病常见的宿主。西藏地区为畜牧区，卫生条件相对较差，牧民与包虫病宿主接触频繁，易通过粪-口途径感染。人感染棘球属绦虫幼虫后，幼虫则会进入人体的门静脉系统，从而滞留于肝脏内，并在肝内逐渐长大，压迫周围肝组织和肝内胆管，常引起肝细胞不可逆损伤和阻塞性黄疸，晚期病死率高，号称“虫癌”［4］。

对于包虫病，目前研究主要集中于预防、诊断及治疗，而国际公认此病的预防要远胜过治疗。在中国，包虫病分布地区比较广泛而且发病人数也较多，包虫病的防治则需要消耗比较多的人力、物力以及财力，同时还要保证防治机制的可持续性，这些问题都增加了此病防治的难度［5-6］。

随着对包虫病研究的不断深入及国家对传染性疾病防控力度的不断加大，西部地区包虫病的发病率显著降低。但包虫病具有高复发率的特点，包虫病预防工作意义深远。国家卫计委于2016年下发了关于包虫病防治的“十三五”规划，将包虫病列为我国重点防治的寄生虫病之一［7］。

目前ARIMA模型在传染病的发病预测中得到广泛应用。比如王永斌等［8］运用此模型预测了我国梅毒的发病率，姚英和沈毅［9］预测了杭州市手足口病的发病趋势。美国学者Box和英国统计学家Jenkins在20世纪70年代提出ARIMA模型，该模型分为两个：简单模型和乘积季节模型，并且发现此模型短期预测精确度高［10］。ARIMA乘积季节模型可以充分的提取趋势信息和季节信息，并能借助模型参数进行量化表达［11］。因其在传染病发病率预测中具有简便、适用和短期预测精度较高的优点，故本文应用ARIMA乘积季节模型预测包虫病的发病率，从而为包虫病的防治提供有效的依据。

然而，ARIMA模型也有其局限性，主要包括以下几点：（1）获得的历史数据较少，所建立的模型的有效性则相对低；反之，收集的数据越多则能建立更为优化的模型。（2）环境因素的改变极易导致预测效果不理想。（3）长期预测精度相对较低。因此为了提高此模型的精准性，在实际工作中，提高数据的准确性是重中之重。如果在研究过程中，研究对象的趋势发生较大变化时，则需要重新收集新的数据，实时对模型进行修正和重新拟合，使该模型的预测结果与当年包虫病实际发病情况一致。