幂级数求和函数的方法探究
2021-05-21 08:48李瑞瑞孙铭娟
海峡科学 2021年3期
李瑞瑞 孙铭娟
(信息工程大学基础部, 河南 郑州 450001)

1 和函数的分析性质


逐项积分后所得到的幂级数和原级数有相同的收敛半径。

逐项求导后所得到的幂级数和原级数有相同的收敛半径。


以上性质告诉我们,幂级数的和函数在收敛区间内,可以逐项积分和逐项求导,并且逐项积分与逐项求导不改变幂级数的收敛半径。在利用该性质求和函数时,我们往往关注性质的前半部分。借助分析性质求和函数常见步骤如下图所示:

2 典型例题
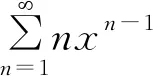
常规解法:先求收敛域。
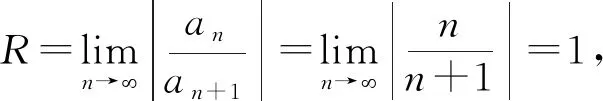

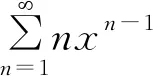
再求和函数:

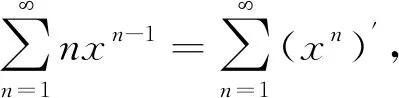
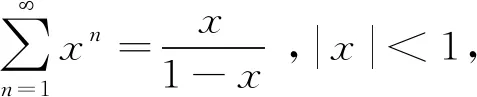
由和函数在收敛区间内逐项可导的性质,得

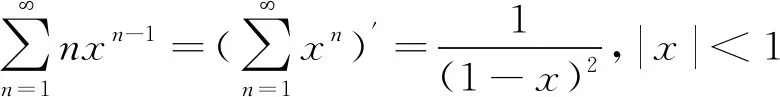

常规解法:先求收敛域。

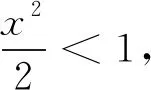
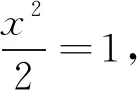

当x=0时,级数显然收敛。
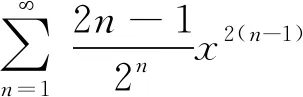
再求和函数:

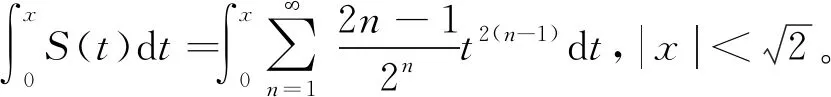
再利用和函数的逐项可积性质

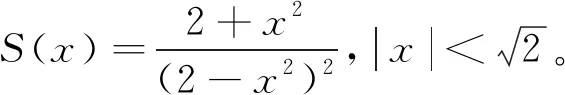
简化解法:
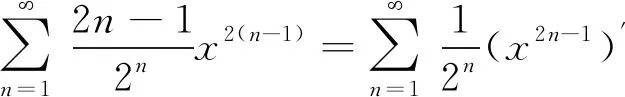

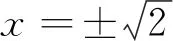
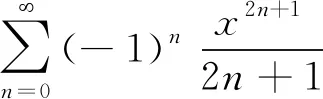

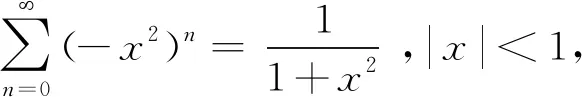
由和函数在收敛域内逐项可积的性质,得:
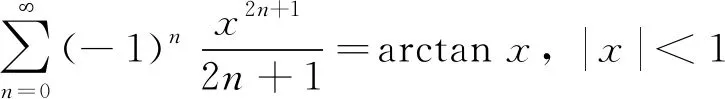

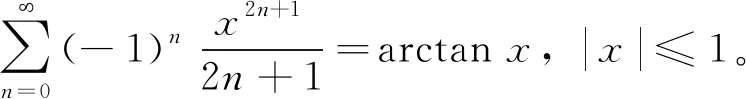
3 结论
通过逐项求导或逐项积分求幂级数的和函数,是求幂级数和函数的一种常用方法,本文利用和函数分析性质中收敛半径不变的特点,由已知到未知,简化求解过程。另一方面,常规解法是“由果索因”的过程,是用分析法处理问题,而上述方法则是“由因导果”,是综合法,两者是可以相互转化的。但是教辅中经常是两种解法灵活运用,对初次接触这类问题的学生来说容易产生困惑,本文通过“由果索因”和“由因导果”区分两种方法,以期使学生的解题思路更加清晰。
猜你喜欢
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26
数学学习与研究(2020年11期)2020-09-11
小学生学习指导(高年级)(2019年4期)2019-11-27
数码世界(2019年8期)2019-08-15
华东师范大学学报(自然科学版)(2019年3期)2019-06-24
中等数学(2018年8期)2018-11-10
小天使·三年级语数英综合(2017年6期)2017-06-07
读写算·小学低年级(2017年5期)2017-05-12
中国科技纵横(2015年22期)2015-10-31
中学生理科应试(2014年12期)2015-01-15

