相似中的“双A”型

文 李长春（特级教师）

教材中的例题和习题都是经过专家反复打磨、精心设计而成的，具有很强的针对性和典型性，也是同学们获取知识和方法、发展能力的重要载体。在“图形的相似”这一章中，就有一个大家非常熟悉的基本图形。

【原题再现】（苏科版数学教材九年级下册第54页例1）如图1，在△ABC中，点D、E分别在AB、AC边上，且DE∥BC。试说明△ADE与△ABC相似的理由。

图1

这是一个基本模型，因为整个图形像个英文字母A，所以我们称它为“A”型。很多试题中都有它的身影。我们先来看看这个模型在习题中的变式。

【习题再现】（苏科版数学教材九年级下册第65页习题6.4第3题）如图2，在△ABC中，点D、E、F分别在BC、AB、AC上，EF∥BC，交AD于点G。

（1）图中有几对相似三角形？是哪几对？

图2

【思路分析】（1）将原图形进行分解，可得到3对“A”型相似三角形，分别是△AEG∽△ABD、△AGF∽△ADC、△AEF∽△ABC；（2）由△AEG∽△ABD，得由△AGF∽△ADC，得所以。

从图形的形状上来看，因为其像两个并排放置的英文字母A，所以我们不妨称其为“双A”型。将第（2）问中的结论变形也可得到我们可以称之为“双A”型性质1。

特别地，当点G为EF的中点时，则点D为BC的中点；反之，当点D为BC的中点时，则点G为EF的中点。我们可以称之为“双A”型性质2。

在解题中若能发现“双A”型，并灵活运用这些结论，往往能解决不少看似无从下手的难题。特选出几例与大家分享。

一、隐藏在正方形中的“双A”型

例1 如图3，在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG、AF分别交DE于M、N两点。若AB=AC=9，求MN的长。

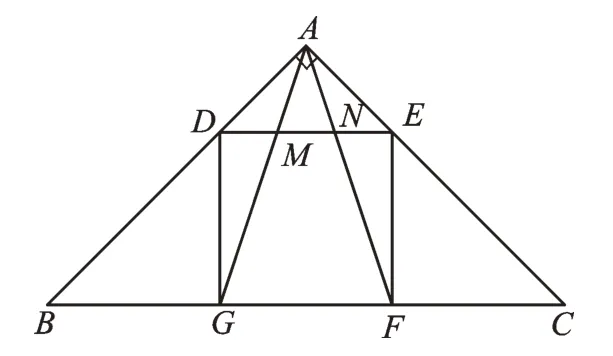
图3

【思路分析】由正方形DEFG得DE∥BC，由“双A”型的性质1可得由正方形DEFG以及AB=AC、∠BAC=90°易得BG=DG=GF，所以DM=MN。同理可得MN=NE，所以。又因为所以MN=。

【总结提炼】本题两次运用“双A”型相似模型，结合正方形和等腰直角三角形的性质，使问题顺利得解。由此可见，在解题过程中，我们若能抓住基本的数学模型，往往能化难为易，化繁为简。

二、隐藏在圆中的“双A”型

例2 如图4，已知AB是⊙O的直径，BC是⊙O的切线，OC平行于弦AD，过点D作DE⊥AB，垂足为E，连接AC与DE交于点P，求证：EP=PD。

图4

【思路分析】如图4，分别延长BC、AD交于点F。因为OC∥AD，所以则BC=CF。因为AB是⊙O的直径，BC是⊙O的切线，所以FB⊥AB。又因为DE⊥AB，所以DE∥FB，而BC=CF，由“双A”型性质2，可得EP=PD。

【总结提炼】本题在补全“双A”型的基础上，以圆的半径相等和OC平行于弦AD为依托，在证得BC=CF后，运用“双A”型性质2找到解题思路。因此，我们要想运用“双A”型，就需要先根据题意发现（或构造出）“双A”型。

三、隐藏在投影下的“双A”型

例3某兴趣小组开展课外活动，如图5，A、B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D处，此时他（CD）在某一灯光下的影长为AD。继续按原速行走2秒到达点F处，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米。然后他将速度提高到原来的1.5倍，再行走2秒到达点H处，此时他（GH）在同一灯光下的影长为BH（点C、E、G在一条直线上）。

（1）请在图中画出光源O点的位置，并画出小明位于点F时，在这个灯光下的影长FM（不写画法）；

（2）求小明原来的速度。

图5

【思路分析】（1）光源O点的位置及小明位于点F时在这个灯光下的影长FM如图6所示。（2）设小明原来的速度为v米/秒，由题意得CE=DF=AD=2v，AM=AF-MF=4v-1.2，EG=FH=2×1.5v=3v，MB=AB-AM=12-（4v-1.2）=13.2-4v。因 为CG∥AB，由“双A”型性质1得所以。解这个方程得v1=0，v2=1.5。经检验，v=1.5为方程的解。

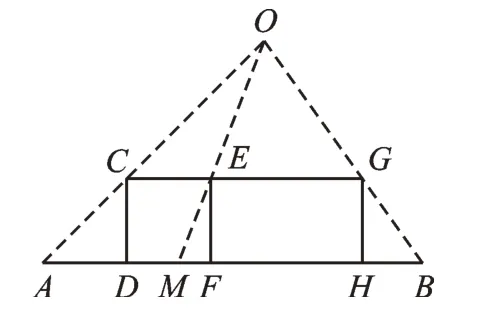
图6

【总结提炼】在补全图形的基础上，出现了“双A”型相似模型，因此，只要我们能够根据已知条件设出小明原来的速度，然后表示出图中相关线段的长，抓住“双A”型，运用其性质，问题就会迎刃而解。