电气化铁路钢轨内阻抗计算研究*

王 东， 张友鹏， 赵 斌

(兰州交通大学 自动化与电气工程学院, 甘肃 兰州 730070)

0 引 言

钢轨作为电气化铁路牵引供电系统的重要组成部分，除了支撑和引导列车运行外，还是牵引电流回流和轨道电路信号电流的共同通道。钢轨阻抗是轨道电路设计中重要的一次侧参数，阻抗大小影响着轨道电路的传输性能[1]。钢轨内阻抗是钢轨阻抗计算中极为重要的一部分，精确计算钢轨内阻抗对于保证轨道电路传输性能和列车运行安全具有重要意义[2]。

交流电流流经钢轨时，由于集肤效应的存在，导致电流分布不均匀，主要集中分布在钢轨表面。集肤效应会导致钢轨交流电阻的增加和内电感的减少。对于圆柱形导体，考虑集肤效应计算导体内阻抗时，可以直接解析求解，但对于像钢轨这种具有不规则横截面的导体，直接求解内阻抗时较为困难。

目前对于考虑集肤效应计算不规则导体内阻抗时，一般采用将不规则导体等效为圆柱体模型的做法[3]。Silvester P等人理论研究了圆柱形导体的集肤效应，为钢轨内阻抗的计算提供了理论依据[4]；Dommel H W和Semlyen A等人分别通过对Bessel函数进行多项式近似和渐近展开计算了圆导线的内阻抗[5,6]；陈彩屏使用Bessel函数计算了大参数下空心圆导线的内阻抗[7]；Hill R J等人基于有限元法研究了钢轨交流内阻抗随电流、频率的变化规律，并与实测数据对比，表明有限元法可用于钢轨内阻抗的计算[8]，但计算所需资源较大；朱峰等人将钢轨等效为圆柱形导体，推导出内阻抗计算公式，并利用多项式近似对Bessel函数进行近似[9]，但是计算与仿真结果同实验数据相比误差较大。

本文在把钢轨等效为圆柱形导体的基础上，分别推导出钢轨在低频和高频时的内阻抗公式。根据Rolle平均值定理和Maclaurian近似公式，对低频和高频时钢轨内阻抗公式进行处理，得到整个频率范围下内阻抗计算公式。利用该计算公式编程计算不同型号钢轨的内阻抗，并分析内阻抗随电流幅值、频率的变化规律。同时，基于有限元法仿真计算钢轨模型，并将内阻抗计算公式的计算结果与有限元仿真结果进行对比，相对误差小于6 %，且仿真结果与计算结果变化趋势一致，从而为牵引供电系统建模时钢轨内阻抗的计算提供了可靠的理论依据。

1 理论推导

1.1 直流内阻抗

导体的直流内阻抗(电阻)与导体横截面形状无关，仅与导体横截面面积、电阻率、长度有关，单位长度导体的直流内阻抗为

ZDC=ρ/S=RDC

(1)

式中S为导体的横截面积；ρ为导体的电阻率。

1.2 交流内阻抗

导体中流过交流电流时，由于集肤效应的存在，导致电流在导体横截面上分布不均匀，电流主要分布在导体表面一定的集肤深度内，导体集肤深度为

(2)

式中 j为虚数单位；ω为角频率；μ=μrμ0为导体的磁导率(μr为导体的相对磁导率，μ0=4π×10-7H·m-1为真空磁导率)。

为方便计算导体交流内阻抗，假设电流在导体集肤深度内均匀分布，得到交流内阻抗公式为

(3)

式中l为导体圆周长度；Shf为集肤深度内电流分布层面积。

为计算整个频率范围内导体的内阻抗，对低频和高频的内阻抗计算公式进行处理。定义函数f(x)在[0,∞]上连续可微，且为非零函数，当f(0)与f(x→∞)已知时，根据Rolle平均值定理及Maclaurian近似公式，f(x)可以表示为

f2(x)=f2(0)+f2(x→∞),0≤x≤∞

(4)

直流内阻抗计算式(1)与交流内阻抗计算式(3)分别对应于函数f(x)的f(0)和f(x→∞)，因此，根据式(4)得到整个频率范围内导体内阻抗为

(5)

1.3 内阻抗的计算

计算圆导线内阻抗时，将涉及到Bessel函数。Schelkunoff公式表明[10]，在频率f→0时，对于圆柱形导体，Bessel函数变量x→0，得到Bessel函数值为

I0(0)=1,x-1I1(x)→1/2,K0(0)=0,K1(x)→1/x

(6)

式中I0(0),I1(x)分别为第一类修正的零阶、一阶Bessel函数;K0(0),K1(x)分别为第二类修正的零阶、一阶Bessel函数。因此，对于频率f→0，根据式(6)中Bessel函数的值，计算低频内阻抗为

ZDC(f→0)=

(7)

式中xi=ri/hc,x0=r0/hc,ri与r0为等效圆柱形导体的内、外半径。

将式(2)中的hc代入式(7)，得到当频率f→0时，导体低频内阻抗为

(8)

当频率较高时f→∞，Bessel函数变量x→∞，得到Bessel函数值为

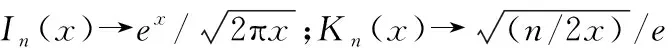
(9)

因此，对于频率f→∞，根据式(9)中Bessel函数的值，计算高频内阻抗为

Zhf(f→∞)=

(10)

根据式(5)对式(8)与式(10)进行处理，得到整个频率范围内导体内阻抗为

(11)

2 钢轨等效模型

由于钢轨横截面不规则，呈“工”字型，与平时常见的圆导线不同，考虑集肤效应时无法直接解析计算内阻抗，因此，将钢轨等效成圆柱形导体。根据钢轨的横截面积和横截面周长，得到等效的圆柱形导体的内半径ri,外半径r0分别为

r0=lr/2π

(12)

式中lr为钢轨的横截面周长；Sr为钢轨的横截面积。

钢轨长度为1 m，钢轨电阻率ρ=2.1×10-7Ω·m，相对磁导率μr=100，根据式(12)计算不同型号钢轨的参数，如表1所示。

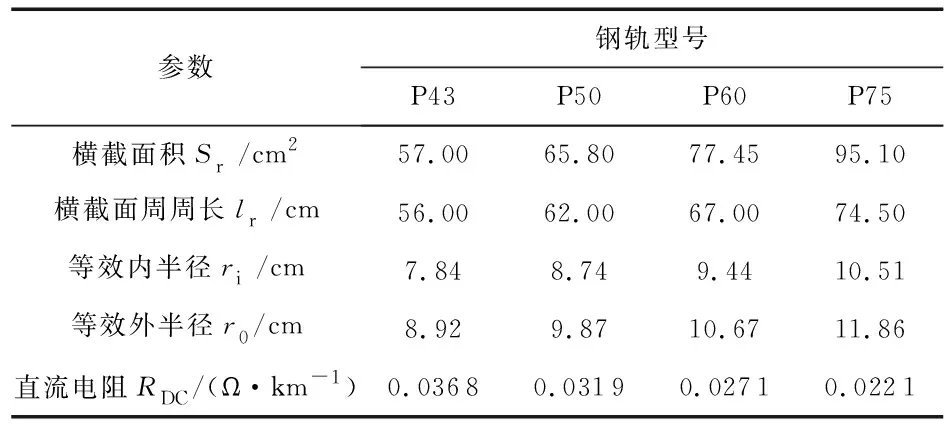
表1 不同型号钢轨的基本参数

3 有限元仿真

以钢轨型号为60 kg/m的P60型钢轨为例，按照钢轨的实际尺寸，1︰1比例完成钢轨模型的绘制，并根据实际情况设置钢轨的材料参数。仿真中，钢轨电阻率为ρ，由于钢轨是铁磁性材料，根据文献[11]，获得钢轨的B-H曲线参数。集肤效应实际是涡流效应的体现，因此在仿真中使用涡流求解器，激励设置为正弦工频50 Hz电流。对模型网格剖分时，考虑集肤效应，根据集肤因子确定网格的大小。钢轨模型剖分结果如图1(a)所示。对模型进行仿真计算，得到钢轨横截面的电流密度分布图，如图1(b)所示，由于集肤效应，电流主要趋向于钢轨表面分布。

图1 有限元仿真

通过计算欧姆损耗和磁场储能，分别得到钢轨交流内电阻与电感，其中电感的计算结果包含模型的外电感和内电感，本文主要研究钢轨内电感的变化规律。当电流频率极高时，电流集中分布在钢轨表面，此时可认为钢轨内部无电流分布，从而得到钢轨外电感，将有限元计算的电感数据减去外电感即为钢轨内电感。

4 钢轨内阻抗影响因素分析

4.1 频率的影响

钢轨是轨道电路信号电流与牵引电流的通道，而轨道电路信号电流的频率范围为1 700～2 600 Hz，牵引电流频率为50 Hz，因此，频率范围较宽。为研究不同型号钢轨内阻抗在较宽频率范围内的变化规律，进行0～10 kHz范围内的扫频。不同型号钢轨的基本参数如表1所示，根据式(11)，编程计算在0～10 kHz范围内钢轨内阻抗随频率的变化规律，计算结果如图2所示，钢轨交流电阻和内电感与频率呈非线性关系。

图2 不同型号钢轨内阻抗随频率变化

从图2(a)可以看出，随着电流频率的增加，钢轨交流电阻逐渐变大，在低频时变化比较明显，而随着频率的增大，变化越来越小。在同一频率下，钢轨横截面越小，其交流电阻值越大。从图2(b)可以看出，随着电流频率的增加，钢轨内电感逐渐减小，在低频时特别明显，而随着频率的增大，钢轨内电感趋于稳定值，且不同型号钢轨的内电感稍有不同。在同一频率下，钢轨横截面越小，其电感值越大，但差值较小。

4.2 电流的影响

钢轨中同时存在信号电流和牵引电流时，信号电流幅值大小为毫安(mA)级，而牵引电流幅值较大，一般为几百安培，因此，研究电流幅值对内阻抗影响时，钢轨中电流主要为工频50 Hz的牵引电流。以P60型钢轨为例，其基本参数如表1所示。由于钢轨是铁磁材料，不同电流幅值下钢轨的相对磁导率将发生变化，所以钢轨内阻抗在不同电流下也将发生明显的变化。利用安培环路定理计算出不同电流幅值所产生的的磁场强度，钢轨相对磁导率μr与磁场强度H之间的函数关系，得到不同电流幅值对应的钢轨相对磁导率μr的值，如表2所示。

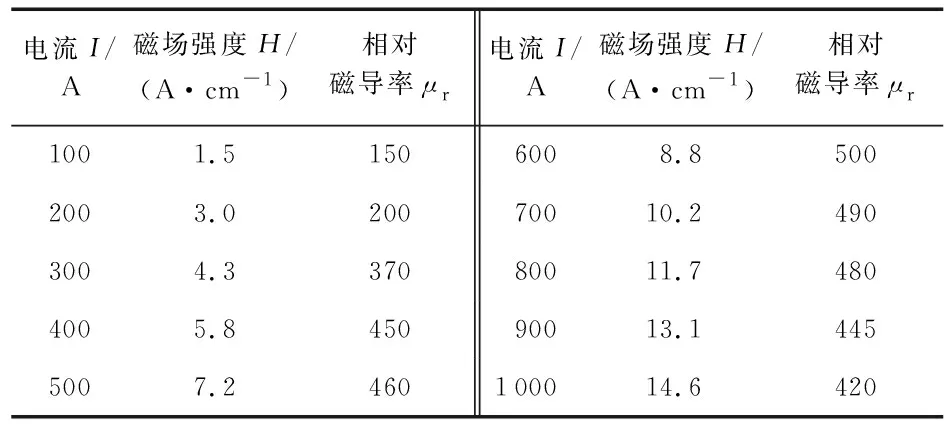
表2 工频情况下不同电流幅值对应的钢轨相对磁导率

在工频(f=50 Hz)情况下，将表2中不同幅值电流对应的磁导率μr的值代入式(11)，得到钢轨交流电阻与内电感随电流幅值变化的规律，如图3所示。

图3 P60钢轨内阻抗随电流变化

从图3可以看出，钢轨交流电阻与内电感先随电流增大而增大，达到最大值后开始缓慢减小，其主要是由于钢轨是铁磁材料，随着电流的增大，将出现磁饱和效应，即磁导率随电流先开始增大，当电流超过某一限定值后，磁导率随电流的增大而缓慢减小，从而出现上述情况。同时也可以看出，计算值与有限元仿真结果变化趋势一致，将两者对比后，相对误差均小于6 %。

5 结 论

1) 考虑钢轨不规则截面和集肤效应计算钢轨内阻抗时，运用本文推导的内阻计算公式，计算结果与有限元仿真结果对比，相对误差小于6 %。

2) 给出了内阻抗计算公式在不同型号钢轨下交流电阻和内电感随频率变化的曲线，表明不同型号钢轨在同一频率下，电阻值差异较大，且横截面越小，电阻值越大，而对钢轨内电感影响较小。

3) 给出了钢轨电阻和内电感随电流幅值变化的规律，表明由于钢轨是铁磁材料，其电阻和内电感随电流幅值的增大呈现出先增大而后缓慢减小的变化趋势。