基于变分模态分解和深度置信网络的短期负荷预测*

姚海强, 张 涛

(安徽大学 电气工程与自动化学院,安徽 合肥 230601)

0 引 言

短期负荷预测作为电网日常规划的基础,是电力安全运行不可或缺的重要部分[1]。随着电力的改革与发展,提升短期负荷预测的准确度成为该领域的研究者的首要任务,它对如何安排调度计划、电力系统可靠运行、经济利益最大化等有着重要意义[2]。

目前,围绕负荷序的时序性和非线性特点,短期负荷预测方法日新月异,主要包括有多元线性回归法[3]、 卡尔曼滤波法[4]、灰色理论法[5]、自回归积分滑动平均模型[6]、支持向量机[7]以及神经网络法[8]等,其中神经网络法应用较为广泛。文献[8]使用了深度置信网络(deep belief networks,DBN)网络对负荷序列进行训练预测,以逐层无监督预训练的方式获取网络的初始参数,解决了传统网络中存在的若干问题；具有好的初始点,对于经常出现在神经网络中的过拟合和欠拟合问题,也可以通过预训练得到有效解决。

但是对于波动性较强负荷序列来说,单一的预测方法获得的预测精度,已经无法满足现阶段的需求。近年来,各种组合预测方法广泛应用在短期负荷预测领域,其中,以经验模态分解(empirical mode decomposition,EMD)为主的分解方法能够实现对原始负荷数据的分解,实现平稳序列和非平稳序列相互分离的目的[9]。但是,EMD方法难以避免模态混叠现象产生,分解得到虚假的本征模态函数(intrinsic mode function,IMF),在预测时产生不利的影响。文献[10]利用变分模态分解(variational mode decomposition,VMD)将负荷数据分解为特征互异的IMF,减轻了模态混叠现象发生,有利于信号的进一步分析。

本文以安徽省某地市负荷数据为研究对象,对负荷数据进行VMD,获得多个特征互异的子序列,分别结合DBN预测,叠加各个预测结果。对比单一的DBN方法和EMD-DNN预测方法的预测结果,验证了本文所提方法可挖掘负荷数据潜在的规律,在减小了计算规模的同时减少了虚假IMF的产生,进而提升预测精度。

1 VMD算法原理

2014年Dragomiretskiy K提出了一种新型的VMD估计方法,它可以自适应地分解非平稳信号,将复杂的信号分解成K个具有稀疏特性的模态分量[11]。不同于EMD和EEMD方法,VMD方法采用了非递归及变分模态求解模式处理原始信号,具有较好的抗噪声性能和非平稳性能信号处理效果,其本质上是一个自适应维纳滤波器组。

VMD的目的是将多分量信号分解为带宽上具有特定稀疏性的有限带宽模式的集合；相反,这些分解的模式也能够重构输入信号。求解约束变分优化问题

(1)

式中uk(t)为输入信号的模态函数；{uk}为模态集合{u1,u2,…,uk}；wk为对应于输入信号的第k阶模态的中心频率；{wk}为分解后的模态对应的一组中心频率{w1,w2,……,wk}；f(t)为输入信号；δ(t)为单位脉冲函数。

将拉格朗日乘子λ和二次惩罚因子α引入,可以将式(1)改写为

L({uk},{wk},λ)=

(2)

使用乘法算法的交替方向法求解式(2),获得一组模态分量及其各自的中心频率。每个模态可由频域中的解估算出来,表示为

(3)

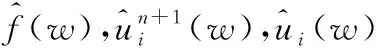
在式(3)中具有维纳滤波结构的特点,它直接更新了傅立叶域中的模态。此外,还可以通过提取滤波分析信号傅里叶逆变换的实部,在时域内得到这些模态

(4)

2 DBN

DBN由若干个限制玻尔兹曼机(restricted Boltzmannn machine,RBM)堆叠构成,它在本质上是多层神经网络[12]。DBN的出现有效地解决了传统神经网络存在的诸多问题,如对输入数据的要求高、收的敛速度慢以及容易陷入局部最优点的难题[13]。

RBM是DBN 的基本构成单元,其结构如图 1(a)。RBM是由2层神经元构成,一层是可视层,用于训练输入数据,另一层是隐含层,用于特征提取。两层之间通过权重矩阵w相互连接。

DBN的训练过程可分为2个阶段:预训练和微调整。在预训练的阶段,使用了无监督式逐层贪心训练的思想,首先随机的选取训练样本,然后输入到DBN,接着训练第一个RBM,目的是让其可以捕获输入数据的一些主要特征,再将它的输出作为接下来RBM的输入。类推循环,一直到DBN完成训练。但是,此时的DBN的输出特性还未能达到最优状态。因此需要进一步处理,在微调整阶段,利用有监督的训练思想,对DBN的权重和偏置量微调,以提高模型预测的精度。图1(b)是DBN网络结构。

图1 网络结构

3 VMD-DBN模型的短期负荷预测

由于人类活动、气象条件、社会经济和政治因素等不同程度的影响,电力负荷表现出一定的波动性、随机性的特点。然而,人类生活生产活动存在一定的规律性,因此,负荷也具有较强的周期特性。为精细研究分析负荷序列的特点,采用VMD方法对原始负荷序列进行分解,得到一系列负荷分量,结合DBN进行训练预测,叠加每个分量预测结果,最终得到了VMD-DBN模型的预测结果,模型框图如图2所示。

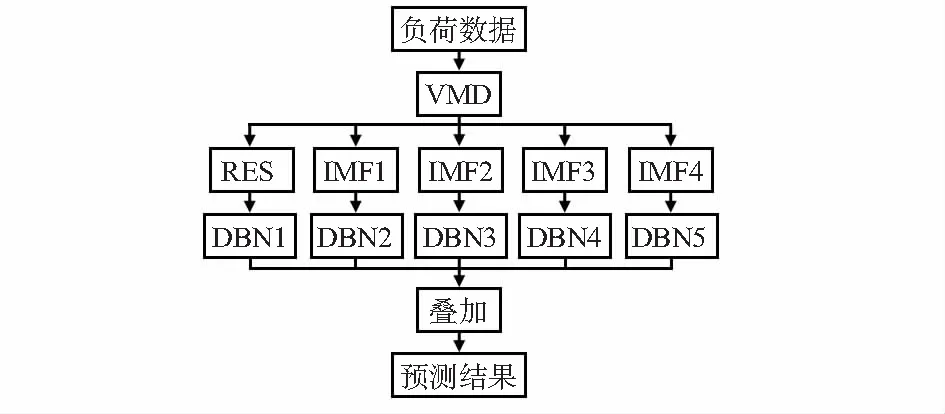
图2 负荷预测模型

经反复实验测试给出了VMD算法的主要参数设置[11]分别见表1。采用枚举法对隐含层神经元个数逐层进行选取,选取结果,第一层20个,第二层15个,第三层25个[14]。

表1 VMD算法的主要参数设置

4 实验分析

实验采用中国某地区2016年06月1日～2016年06月10日之间的实际负荷数据,采样频率15 min,共计采样点960个,前面8天的数据作为训练样本,后面2天的数据作为测试样本。对原始数据集分别采用EMD和VMD方法进行分解,原始负荷序列及两种方法的分解结果分别见图3。

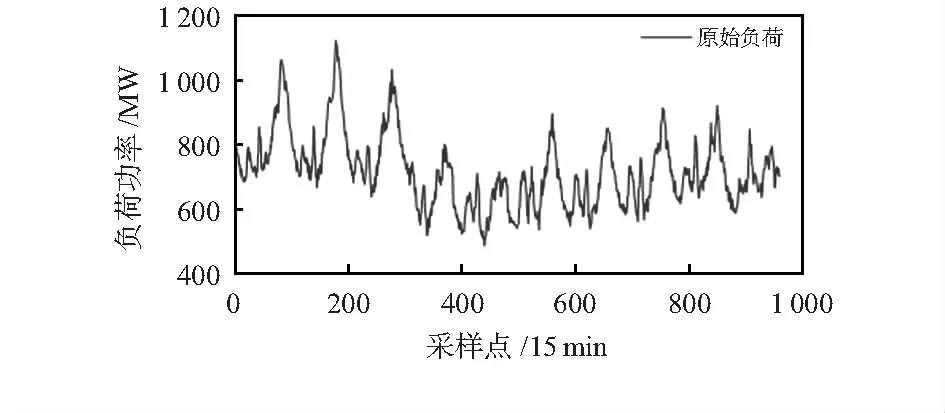
图3 原始负荷序列

从图3中可以看出,原始负荷序列的波动性较强,图4可以看出,由EMD分解的结果分量多达8个,而VMD分解的结果分量只有5个,这可以减少预测的计算量；高频分量是不利于预测的,图4(b)可以看出VMD分解出来的高频分量幅值占比很小,这有利于减少预测的误差；中低频部分VMD分解的分量的规律性则明显比EMD分解的分量规律性要强；两者分解出来的低频部分都较为平缓,可以看出VMD分解出的低频分量更接近原始负荷序列的波动趋势。因此,从两者分解结果来看VMD方法更有利于后续建模预测。

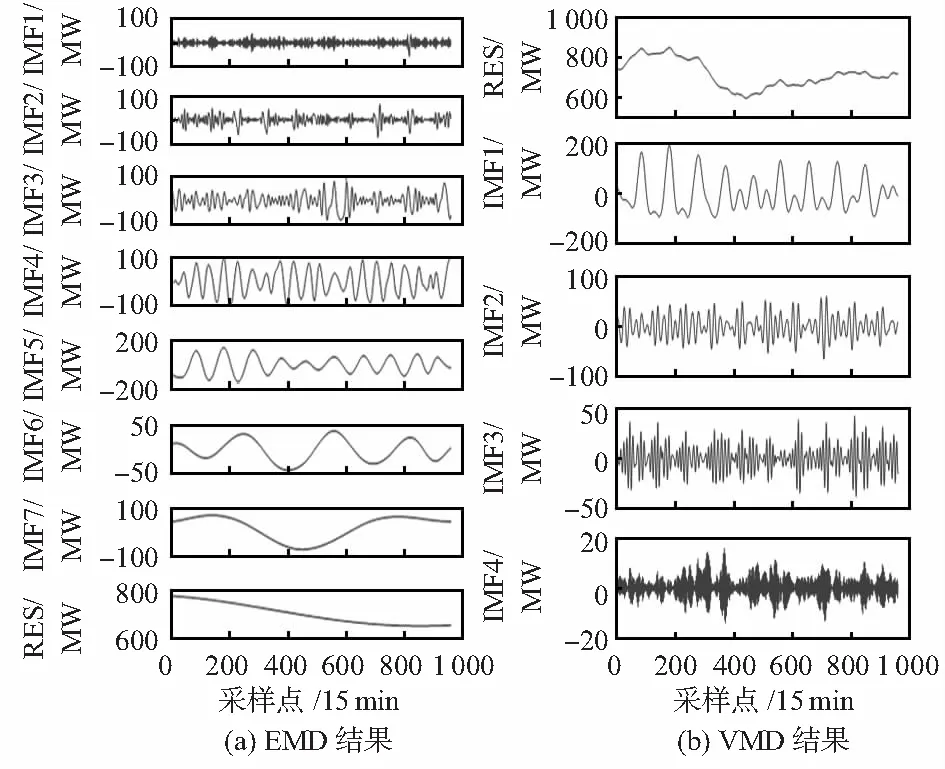
图4 二种方法分解结果

采用DBN对分别对原始负荷数据、EMD及VMD分解的分量进行预测,并分别叠加后两种方法的预测结果,得到EMD-DBN和VMD-DBN的最终预测结果。图5中给出了三种方法的预测结果。采用平均绝对百分误差(mean absolute percentage error,MAPE)和均方根误差(root mean square error,RMSE)作为预测模型评价指标。三种方法的误差统计结果见表2。

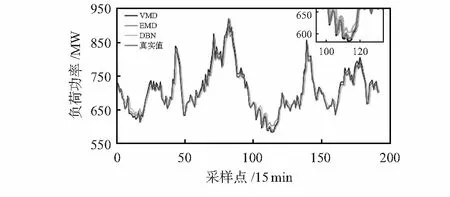
图5 三种方法的预测结果比较

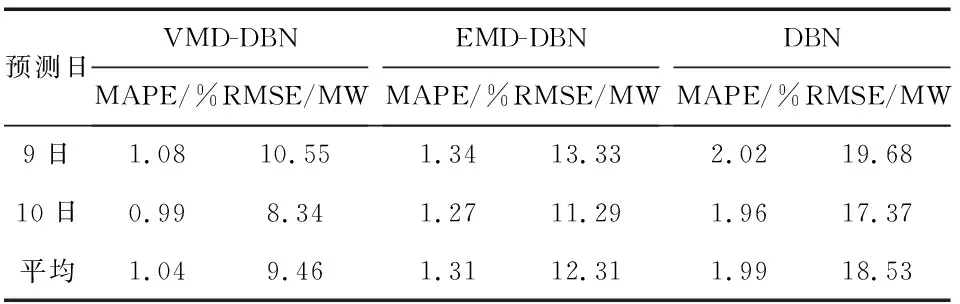
表2 三种方法的误差统计结果

图5中的右上角的放大区域中可以看出单一采用DBN方法在负荷峰值部分预测误差最大,而VMD-DBN方法略优于EMD-DBN方法,预测结果精度很高。在表2中,从预测日的平均值可以看出,VMD-DBN方法的具有最好的预测精度,MAPE为1.04 %,RMSE为9.46 MW,验证了该方法具有较好的预测精度。

5 结 论

本文提出了一种基于VMD-DBN的短期负荷预测方法。经过实验验证,在波动性较强的负荷序列中,VMD可有效提取挖掘其内在特性。对比EMD方法,VMD方法可手动调节模态分量个数,进而可减少预测的计算规模。同时,考虑到DBN具有预训练方式的特点,可有效缓解传统神经网络易陷入局部最优点问题,可为高精度预测结果提供强力保障。对比DBN和EMD-DNN方法,突显了本文方法优越的预测性能,为研究短期负荷预测提供一定的参考意义。

在后续的工作中,考虑在输入数据中加入影响负荷变化的特征；考虑结合粒子群优化算法,对DBN的权值和阈值进行逐层优化,提升其预测性能。