基于混合蛙跳算法的极限学习机软测量建模*

孙顺远, 周 乾

(1.江南大学 物联网工程学院,江苏 无锡 214122; 2.轻工过程先进控制教育部重点实验室,江苏 无锡 214122)

0 引 言

由于工业现场高温高压、强酸强碱、强干扰等恶劣环境，很难直接采用硬件传感器监测关键质量变量。通过软测量技术，构建辅助变量和主导变量之间的数学模型，能够对关键质量变量进行实时准确地预测，解决生产过程中质量变量测量滞后、在线分析仪表价格昂贵的问题。因此对于软测量的研究[1～4]至关重要。目前，常用的建模方法有支持向量机(support vector machines,SVM)[5]、高斯过程回归(Gaussian process regression,GPR)[6]、极限学习机(extreme learning machine,ELM)[7,8]等。在软测量建模算法中，ELM具有结构简单、学习速度快、参数少等优点，并克服传统神经网络多次迭代的缺陷，收敛速度快，常应用在基于数据驱动的软测量建模中。ELM虽能取得较好的建模效果，然而其建模过程中很难精确找到最优参数，导致学习能力不足，影响到ELM的预测精度及稳定性。因此，需要对ELM的参数进行寻优，以提高ELM建模的预测精度。混合蛙跳算法(shuffled frog leaping algorithm, SFLA)[9,10]利用种群内青蛙的数次迭代，找到局部最优解，再进行混合跳跃，进行全局信息的交换，如此循环多次，找到一个全局最优解。SFLA能够跳出局部最优的困境，增强全局搜索能力，是一种被广泛应用的智能优化算法。

本文运用SFLA对极限学习机进行优化，寻找最优的激活函数速率参数和位移参数以及岭回归中的乘法因子。SFLA能加快对全局最优解的搜索，加快网络收敛速度，从而克服ELM预测不稳定、参数难确定的问题。最后，将SFLA-ELM应用于脱丁烷塔塔底丁烷浓度的预测和污水处理过程中生物需氧量的预测中，与不同的建模方法比较，验证了SFLA-ELM的有效性、准确性。

1 预备知识

1.1 ELM算法

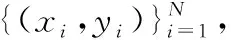
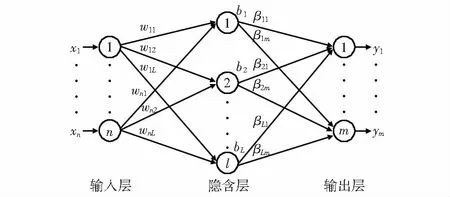
图1 ELM结构

ELM的训练目标是最小化预测误差，从而求得输出权重，可表示为

(1)

式中λ为惩罚因子，ei为预测误差。

将约束项代入第一项，得到等价无约束优化问题并转换为岭回归问题，将LELM相对于β的梯度设为零，整理后得到

β=(HTH+λI)-1HTY

(2)

式中H为隐含层输出矩阵。

1.2 SFLA

SFLA是模拟自然界中青蛙觅食过程而产生的启发式搜索算法。将青蛙分成若干个种群，在同一种群中的青蛙可以进行信息传递，向食物源靠近，实现局部寻优。每隔一段时间，混合策略将各种群中的局部信息进行全局信息交换，然后重新进行分组寻优。将局部信息和全局信息更替迭代寻优，直至寻找到食物。

SFLA的过程如下：

步骤1 初始化青蛙种群，确定青蛙数量F，种群个数m，青蛙位置的维度d，子种群内部迭代次数nei，青蛙种群全局混合迭代次数Nei。

步骤2 确定适应度函数q(x)，计算每只青蛙对应的适应度值。

步骤3 根据F只青蛙的适应度函数值进行升序排列，并均匀分配到m个种群中。得到每个子种群中的最好个体Xb和最差个体Xw以及局最好个体Xg。

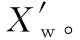
步骤5 达到总种群的迭代次数，输出总种群中位置最佳的青蛙，即全局最优解。

2 基于SFLA的极限学习机训练算法

在ELM的软测量建模中，需要先确定隐含层神经元的个数，再随机赋值给输入权值和偏置，接着根据激活函数计算出隐含层的神经元输出矩阵H。ELM中激活函数的选取对模型的训练效果有着重要影响。激活函数有以下几种形式

(3)

传统的激活函数为g1(x)，其函数图像如图2所示。

图2 g1(x)的曲线图

在传统的激活函数g1(x)的基础上添加速率参数a可控制其变化速度变成g2(x)。图3(a)为参数a<1时g2(x)的函数图像，图3(b)为参数a>1时g2(x)的函数图像。结合图1,图2,和g1(x)，g2(x)添加参数a后，可以控制曲线上升的变化速度，当a<1时，曲线的变化得相对平缓;反之,当a>1时，曲线变化得相对陡峭。

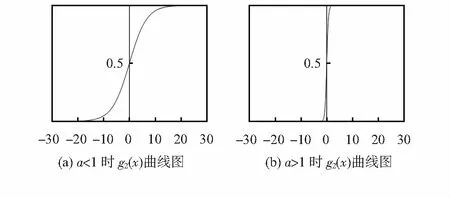
图3 g2(x)曲线图

更进一步，在g2(x)的基础上增加位移参量c使之成为g3(x)。g3(x)的函数图像如图4所示，可以发现位移参量c能够对g2(x)进行平移。

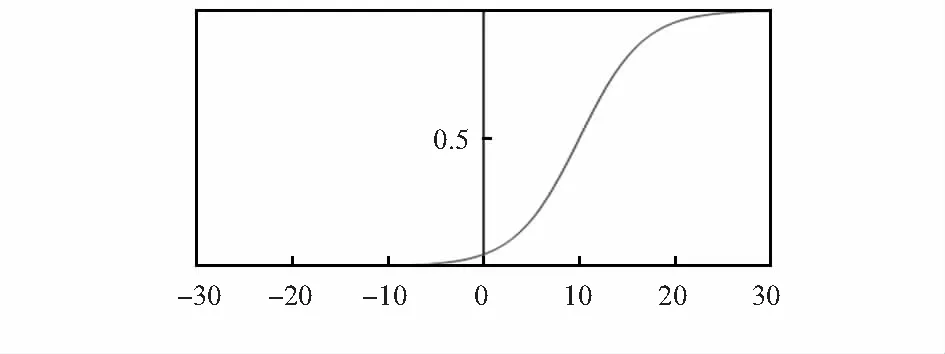
图4 g3(x)曲线图

综合分析激活函数的三种形式以及图2～图4可得，引入了参数a后，可以控制函数上升的速度，对于样本数据中较接近的数据，加入参数a后的适应度函数值差距不大，有利于寻优效果；而位移参量c能够对函数图像进行平移，当数据样本分布不集中，能够有效计算出相应的适应度函数值。因此，本文运用寻优能力强的混合蛙跳优化算法，对速率参数a，位移参数c以及惩罚系数λ进行优化，使得预测误差降到最低。

3 仿真研究

为了验证本文方法的有效性，进行污水处理过程的仿真实验，使用三种不同的建模方法进行建模：方法一是包含激活函数g1(x)的极限学习机软测量模型；方法二是包含激活函数g3(x)的ELM软测量模型；方法三是基于SFLA的ELM软测量模型，其中激活函数同方法二。

工业过程中常使用活性污泥进行污水处理，由于污泥中的微生物降解有机物过程中需要相应的溶解氧量，故用生物需氧量(BOD)作为衡量水质污染程度的关键参数。工业废水处理常用的工艺是活性污水处理法，主要包括5个部分：预处理，初沉，曝气，二次沉淀和污泥回流[11]，其过程如图5所示。

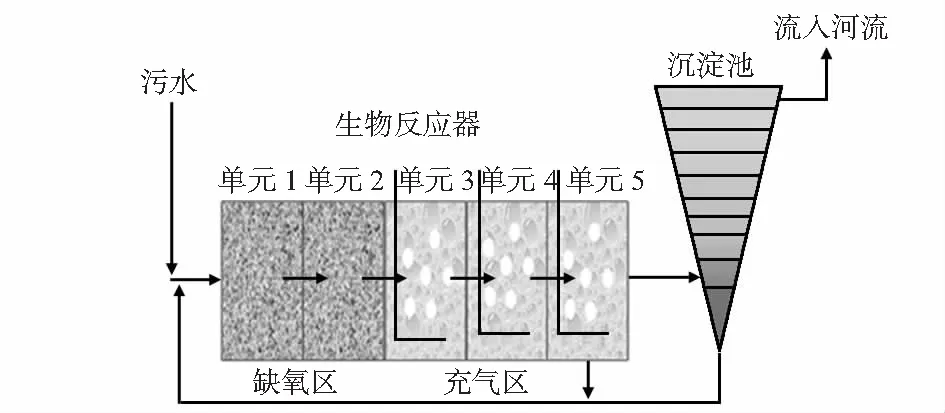
图5 活性污泥法工艺示意

为验证本文建模方法的有效性，采用加州大学数据库(UCI)的污水数据库，其中，19个辅助变量，各个辅助变量的描述如表1所示，1个主导变量为出水BOD含量。共194组数据样本，选取其中的97组作为训练样本集，剩余97组作为测试样本集。采用均方根误差(RMSE)和相关性系数(COR)衡量建模的精度

(4)

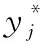
表1 污水处理过程选取的辅助变量表

三种方法对应的预测性能指标如表2所示。对比方法二，方法一的各项性能指标都较低，表明采用传统激活函数g1(x)的模型不能充分挖掘数据样本间的联系；而方法二中的激活函数g3(x)能有效结合数据样本的非线性特征，进而提高模型的预测精度；对比方法二，可看出方法三具有明显优势，表明方法三能够解决工业过程中数据复杂的问题，通过SFLA算法寻找到适合模型的最优参数从而建立精度最高的模型。

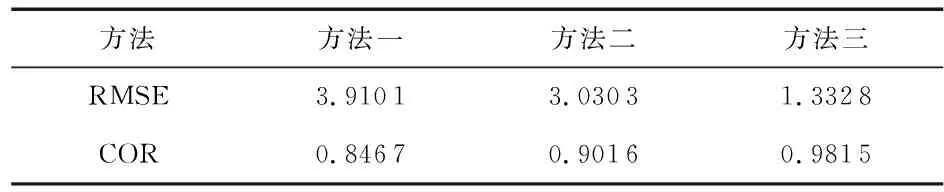
表2 两种方法的RMSE

图6为三种建模方法的预测结果。

图6 三种方法对BOD含量的仿真效果

对比方法一，在数据样本的峰值区域附近方法二的输出值与实际值较接近，训练效果更好，说明方法二能较好地处理非线性数据；对比方法二，方法三利用SFLA算法全局寻优的性能得到模型的最优参数，并将其作为模型的最终参数，该种模型训练效果最佳，预测精度亦最高。

4 结 论

由于工业过程中关键质量变量难以获取，于是将易测得的过程辅助变量对质量变量进行软测量建模。由于ELM模型中参数选取的随机性，易造成模型精度不稳定的问题。因此，本文运用SFLA优化ELM网络中激活函数的速率参数a和位移参量c以及最小二乘中的惩罚因子λ，加强了模型的准确性和可靠性。通过对污水处理和脱丁烷塔过程的仿真实验，验证了本文方法的有效性。