基于GPU的BBPSO-PF算法及其在故障检测中的应用*

曹 洁， 胡文东， 王进花， 余 萍， 赵伟吉

(1.兰州理工大学 计算机与通信学院, 甘肃 兰州 730050；2.兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050；3.甘肃省制造业信息化工程研究中心,甘肃 兰州 730050)

0 引 言

变速恒频的双馈发电机主要包含了空气动力系统、变桨距系统、传动系统、控制器和功率转换系统等[1]，变桨距系统主要用于桨距角的控制，以适应多变的风速，由于该系统频繁地在停止与启动状态间跳变，导致发生故障的概率较高，因而提高该系统故障诊断的准确度和实时性具有重要的意义。

粒子滤波(particle filtering, PF)算法是一种基于蒙特卡洛与递推贝叶斯估计的概率统计算法[2]，可以有效地处理非线性、非高斯噪声环境下的状态估计问题，被广泛用于目标跟踪[3,4]、故障诊断[5,6]、机器人定位[7]、人脸跟踪[8]等领域。而变桨距系统是一个典型的非线性、强耦合系统，故PF算法适合于该系统的故障诊断。PF算法具有多种重采样方法，经典方法包括有多项式重采样(multinomial resampling,MR)、系统重采样(systematic resampling,SR)、残差重采样(resi-dual resampling,RR)和随机重采样(random resampling,RAR)。在状态估计中，当粒子数足够多时，一定程度上提高了状态估计精度，但在粒子数较少的情况下，存在粒子退化和样本贫化等现象。基于此，国内外许多学者对PF算法进行了改进，主要分两种: 一是引入遗传算法(GA)思想改进的PF算法(GA-PF)[9]；另一种是引入粒子群优化(PSO)思想改进的PF算法(PSO-PF)[10，11]。

在对PF算法进行改进的现有研究中，虽然提高了算法的精度，但同时增加了算法复杂度,难以将其应用到实时性要求较高的领域中。为了解决这一问题，研究学者利用图形处理单元(graphic processing unit,GPU)的多线程优势，提出以并行计算的方式提高算法实时性。文献[12]提出了一种并行规约的差分进化粒子滤波方法，解决粒子滤波计算速度问题。文献[13]提出了利用GPU平台并行实现粒子滤波算法，提高计算速度。通过GPU并行实现粒子滤波算法虽然能够提高算法实时性，但粒子滤波算法在重采样环节中粒子之间交互频繁，不能充分发挥出GPU的并行优势。

本文提出一种基于GPU的骨干粒子群优化PF故障检测方法，该方法利用骨干粒子群算法优化PF算法重采样环节，提高算法精确度，同时利用骨干粒子群算法所具有的并行结构特点，将结合后的算法并行化，提高算法实时性。最后将其应用到故障检测中，提高故障检测的精确度和实时性。

1 算法简介

1.1 PF算法

PF算法可以有效地处理非线性、非高斯噪声环境下的状态估计问题，基本思想是利用随机样本集合对条件后验概率密度函数进行近似估计，从而计算样本均值得到状态估计结果。

从先验概率密度p(xk-1|y1︰k-1)中采样N个样本点，得到后验概率密度为

(1)

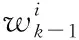
通过多次迭代，根据粒子权重对粒子进行更新，最后对粒子权重进行归一化,对例子加权求和，得到状态估计结果。

1.2 骨干粒子群优化算法

骨干粒子群优化(bare bones particle swarm optimization，BBPSO)算法利用全局最优值和局部最优值进行高斯采样来完成粒子位置的更新，无需粒子交互。与经典的粒子群算法相比，BBPSO算法消除了惯性系数、数度阈值、加速系数等控制参数，使得算法结构更为简洁且易于操作。粒子的位置更新方程为

Xij(t+1)=N(uij,σij)

(2)

uij(t)=0.5(pij(t)+Gij(t))

(3)

σij(t)=|pij(t)-Gj(t)|

(4)

在式(2)～式(4)中，Xij(t+1)为t+1时刻粒子i位置的第j维分量i=1,2,…，I；j=1，2，…,D；其中，I为种群规模；D为带求解问题的维数；pi为粒子i自身的最优位置(即pbest)；G为群体最优位置(即gbest)；符号N(uij,σij)为高斯分布。

由以上公式可知，粒子的位置更新是通过以pbest与gbest的算术平均值uij，pbest与gbest的距离为标准差σij的高斯采样得到的。该算法也需要局部最优值(即pbest)和群体最优值(gbest)的更新，更新方程如下

(5)

(6)

式(5)，式(6)中,pi(t)为第i个粒子自身最优位置(即pbest)，G(t)为群体最优位置(即gbest)，f(t)为算法中的适应度函数。

1.3 并行的BBPSO-PF算法

在状态估计中，PF算法经过数次迭代之后会出现粒子贫化现象。利用BBPSO算法优化PF算法(BBPSO-PF)，通过BBPSO算法的局部最优解和全局最优解两个参数构造高斯函数进行高斯采样。而BBPSO算法结构简单，每个粒子种群分别利用自己的局部最优解与全局最优解联合进行粒子更新。粒子种群相互独立运行，适合并行实现。可以利用该算法取代PF算法重采样环节，克服PF算法重采样环节不能充分并行的缺点。

首先设置初始状态，通过PF算法的状态方程进行状态更新，利用测量方程初始化该时刻的状态估计粒子，并将初始化的粒子传递给BBPSO算法进行处理，根据提前设置好的迭代结束条件结束重采样，BBPSO算法将得到的状态估计结果传送到PF算法中进行状态的更新。算法流程如下：

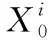
步骤2 重要性采样阶段,k=k+1,采样ik～q(Xk|Xi0︰k-1,Z1︰k)。计算适应度值。利用适应度值寻找个体最优值(pbest)和全局最优值(gbest)。

步骤3 选择阶段(重采样)根据式(2)～式(4)更新粒子。根据式(5)和式(6)更新pbest和gbest。判断是否达到迭代终止条件，若达到终止条件，则执行步骤2，若否则执行步骤3。

并行的BBPSO-PF算法结构流程图如图1所示，可以看出，BBPSO算法在求粒子适应度、个体最优值、粒子更新时都是以粒子群为单位，相互独立运行，这种结构适合利用多线程并行实现，将其应用到PF算法的重采样环节能够解决PF算法重采样环节不能充分并行的问题。

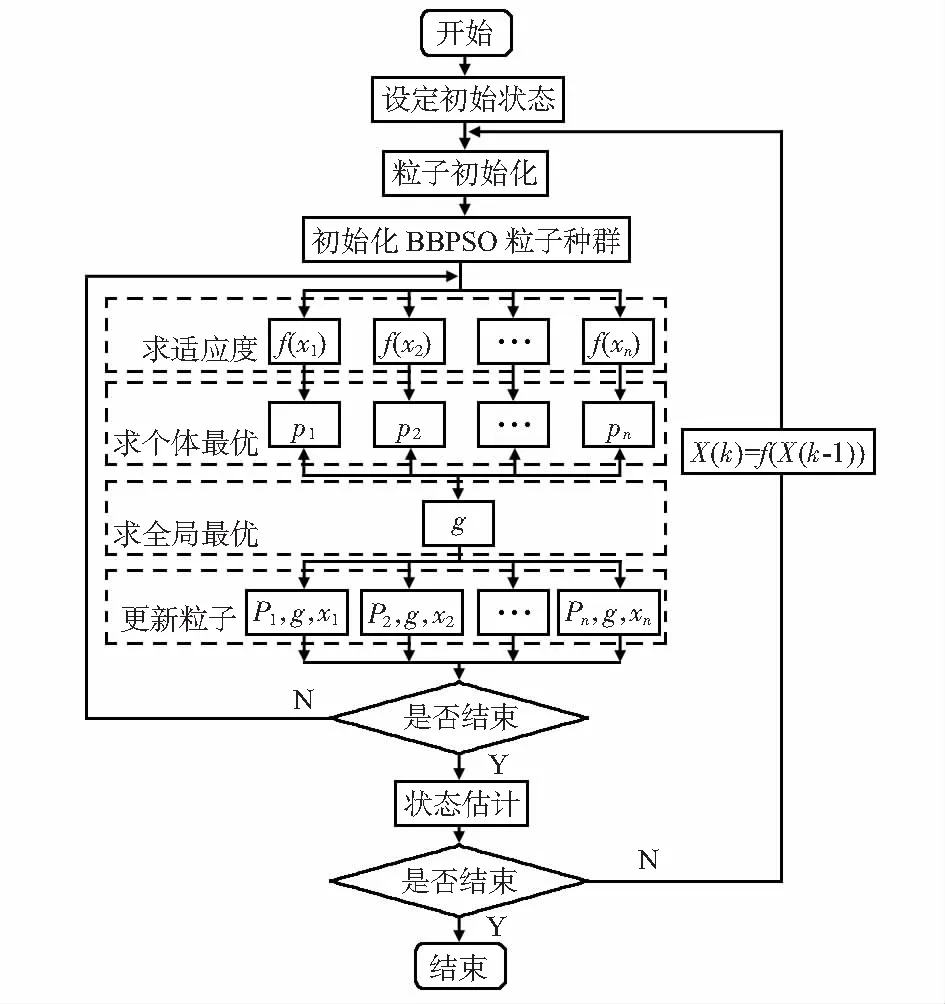
图1 并行的BBPSO-PF流程框图

2 实验仿真与分析

2.1 实验模型

在相同条件下对BBPSO-PF算法和4种不同重采样方法的PF算法从精确度和实时性两个方面进行分析和比较，观察5种算法的性能。本文采用一个广泛应用的标量模型，其状态模型和观测模型为

(7)

(8)

实验参数的设置：初始状态设置为x0=0.1；状态噪声wk～N(0,0.1)；观测噪声Vk～N(0,0.1)；仿真周期T=50。

2.2 算法精度对比

图2给出了粒子数N=6 000时，不同重采样方法的PF算法状态估计结果。由图可见，BBPSO-PF粒子滤波算法状态估计结果更接近真实状态值。

图2 状态估计结果

2.3 算法实时性对比

在Window7系统下采用 VisualStudio2013(CUDA7.5)开发环境进行实验， CPU为Intel®CoreTMi3—4150，GPU为NVIDA GeForce GTX 950。在CUDA架构上并行实现BBPSO-PF算法和4种不同重采样方法的PF算法，对比运行时间。为了排除实验的偶然性，本次实验采用多种粒子数进行分析对比，每组粒子数均重复运行10次，求取平均运行时间，实验结果如图3所示。可以看出BBPSO-PF算法的实时性优于其它重采样方法的PF算法，表明了基于GPU的BBPSO-PF算法可以有效地提高算法实时性。

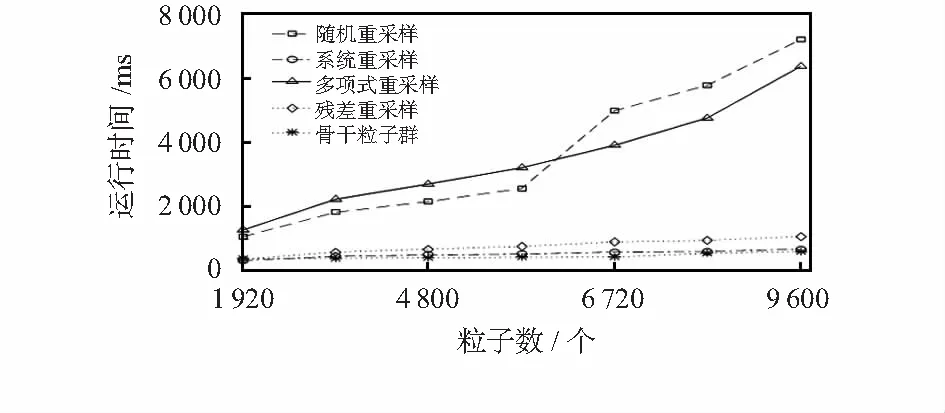
图3 算法并行执行时间

3 BBPSO-PF在故障检测中的应用

3.1 故障类型设计

选择文献[14]中提供的风力机桨距系统的数学模型，根据该数学模型建立的二维状态空间模型如式(9)所示

(9)

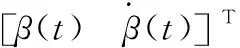
将固定阈值设置为0.1，若系统状态估计测量值与真实测量值的残差超过固定阈值，则认为系统出现故障。

3.2 故障检测结果及分析

利用BBPSO-PF算法进行状态估计，图4分别为突变故障、缓变故障和混合故障的故障检测结果。可以看出，PF算法和BBPSO-PF算法在对应的时间点都能检测出相应的故障。但在正常状态的时间段里，PF算法多次将正常状态检测成故障状态，而BBPSO-PF算法出现该情况较少。从而验证了BBPSO-PF算法能很好地提高算法精度。

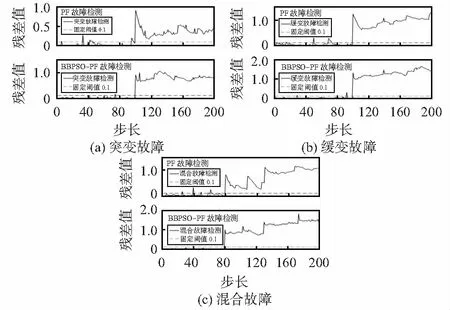
图4 三种故障检测结果

表1记录了5次随机重采样方法和BBPSO-PF算法故障检测时间及均值。由表1可见，在GPU上利用BBPSO-PF算法进行故障检测相较与串行PF实时性提高了94.7 %，相较于并行的PF算法实时性提高了89.8 %。

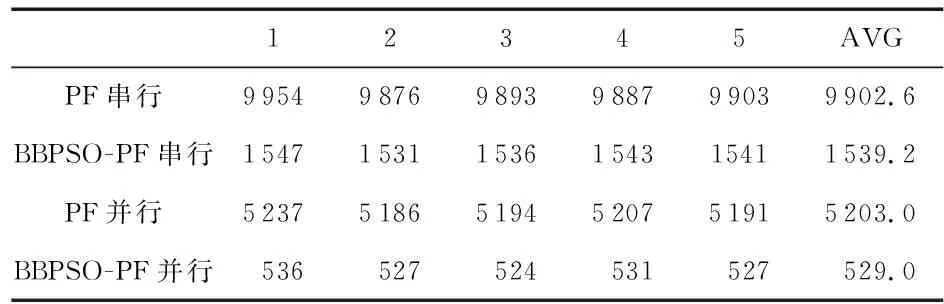
表1 故障检测时间 ms

4 结 论

针对PF算法在精确度和实时性两个方面存在的问题。本文提出面向GPU的BBPSO-PF的故障检测方法，该方法提高故障检测的精确度和实时性。本文的主要内容和结论:1)利用BBPSO算法以全局最优值和局部最优值联合进行高斯采样的特点，将其与PF算法相结合，提高PF算法的精度。2)利用BBPSO算法具有并行结构的特点，取代PF算法重采样环节，解决其不能充分并行的问题。3)将面向GPU的BBPSO-PF的故障检测方法应用到变桨距系统的故障诊断中。实验结果表明，该方法对故障检测的精度和实时性皆有很大的提高。