弹性轴承有限元仿真收敛性分析研究 *

刘 畅,于富侃

(中国直升机设计研究所，江西 景德镇 333001)

0 引 言

随着直升机技术的快速发展与各种新工艺、新材料的应用，直升机旋翼系统已逐渐使用具有橡胶与金属夹层结构的弹性轴承来代替常规金属轴承，目前已广泛应用于直升机旋翼系统中。

球面推力弹性轴承，即所谓的弹性轴承，是球柔性桨毂与星型柔性桨毂的核心弹性元件[1]。其利用弹性轴承轴向压缩、扭转以及弯曲的三种运动形式，代替了传统铰接式桨毂的金属挥舞铰、摆振铰和变距铰。从而在很大程度上简化了桨毂的结构，减少了桨毂零部件数量，提高了桨毂使用寿命，降低了整体制造成本，优化了维护流程。

弹性轴承的工作部分，是由橡胶和薄球碗形状金属两种材料相互叠层间隔组成[2]。弹性轴承最重要的部分，就是橡胶和金属隔片复合叠加而形成的弹性体叠层，弹性体叠层用于传递弹性轴承的承受载荷，通过弹性体叠层中橡胶层的剪切变形来实现弹性轴承的所有变形。在这种承力特性条件下，其轴向压缩刚度越大，则整体承载能力越强，但是会导致弯曲刚度和扭转刚度的增大。从减小操纵载荷以及设计合理性的角度出发，期望在轴向压缩刚度大的同时减小弯曲刚度和扭转刚度。因此，球面推力弹性轴承的设计需对多个要素进行综合考量，合理分配设计过程中存在的多个矛盾要素，使得弹性体隔层，一方面可以满足刚度要求，另一方面又可以降低橡胶层的应力水平，使得橡胶层的疲劳寿命得到提升。使用有限元分析计算软件，可以相对准确地预测弹性元件中橡胶层的疲劳寿命，从而反过来指导弹性元件的正向设计，获得轴向压缩刚度高、操纵性好的弹性轴承。但在有限元分析过程中，常常会出现计算难以收敛的情况，笔者针对弹性元件有限元仿真收敛性进行相关分析。以期对弹性轴承刚度有限元仿真计算提供网格划分依据。

1 弹性轴承仿真工况

随着电子计算机的飞速发展，有限元分析方法迅速发展起来，它被广泛应用于运动学动力学分析、结构强度的校核优化、疲劳寿命计算、热传导、电磁场、流体力学等学科中。有限元计算模型的收敛性是其应用于上述领域的基础，影响有限元计算模型收敛与否的因素很多：模型复杂程度、材料本构参数、实体与实体间的接触设置、施加载荷的顺序及剧烈程度、网格划分方式、单元类型等。文中仅从网格单元方面入手，保持其他有限元仿真工况不变，对弹性轴承有限元仿真收敛性进行分析。

1.1 橡胶超弹性本构模型介绍

橡胶材料的有限元仿真分析不同于一般的传统材料，需要采用超弹性本构模型理论进行仿真计算。一般来说，超弹性本构模型可分为两类：一类是基于统计热力学的模型，另一类是基于连续介质力学的模型。目前多数橡胶采用基于连续介质力学的本构模型[3]。

在研究橡胶变形时，基于连续介质力学的模型，认为橡胶是一种具有各向同性特征的超弹性材料，橡胶的变形属于均匀变形，应变能函数可用主伸长率或者变形张量的不变量来表示。

Mooney-Rivlin本构模型属于是基于应变不变量的一种本构模型，如下式：

式中：WM-R为Mooney-Rivlin本构模型应变能函数，C10、C01为材料常数；Di(1,2,…,n)为与温度有关的材料常数；Jel为材料弹性体积比。Mooney-Rivlin是橡胶有限元仿真中广泛应用的一种超弹性本构模型，其可以在小应变以及中等应变的条件下较为准确地预测橡胶的力学行为。但再橡胶大变形时的陡升行为条件下，该模型在精确度上低于其他模型[3]。

Ogden本构模型是基于伸长率的本构模型，如下式：

式中：Wogden为Ogden本构模型应变能函数；μn、αn为材料常数，(N取值常为2,3,4)。Ogden模型在与实验数据拟合过程中通过自由调整级数的项数，可以很好地和实验曲线相拟合，但是不同实验所确定的常数很可能不协调。

泊松比在(0.48,0.50)区间之内的材料认为是体积不可压缩材料，一般而言，橡胶的泊松比在(0.48,0.488)区间，因此橡胶可以被认为是一种体积不可压缩的材料，即Jel=1。据此，可将上述各超弹性本构模型进行相应的简化。

概括来说上述两种本构模型，Mooney-Rivlin本构模型模拟速度快，但精度较低；Ogden本构模型精度更高，但计算速度较慢。文中利用Mooney-Rivilin进行仿真计算分析。

1.2 弹性轴承仿真计算工况

此次仿真采用某型弹性轴承进行仿真计算。实体模型如图1所示。

将弹性轴承中橡胶本构模型设置为Mooney-Rivlin，具体参数见表1。隔片以及金属接头材料参数见表2。

表1 Mooney-Rivlin本构模型参数

表2 隔片及接头材料参数

添加材料后的弹性轴承如图 2所示，图中浅灰色为橡胶层，深灰色为金属隔片，上下两端部分为金属大小接头。

图1 某型弹性轴承 图2 弹性轴承材料分布

固定弹性轴承的大接头部分，在小接头施加轴向压缩力，所施加的轴向压缩力最大值为105 kN。此次计算分5个分析步依序加载，各分析步加载时间及轴向压缩力值如表3所列。

表3 分析步及载荷

网格是影响弹性轴承计算收敛性的重要因素。Abaqus软件自带网格划分工具可以实现对弹性轴承的网格划分。文中通过改变橡胶与金属网格层数和改变整体网格种子数两方面来对弹性元件仿真收敛性进行探讨。图3为划分网格后的模型。

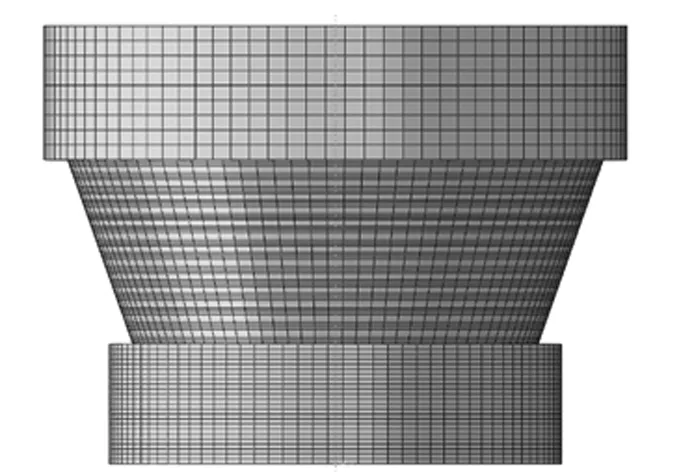
图3 弹性轴承网格划分情况

2 仿真收敛性分析

2.1 整体种子数对收敛性影响

首先设定橡胶层网格层数为3，金属网格层数为1。不同整体种子数模型收敛性如表4所列。各种工况模型仿真刚度与轴向压缩力关系如图4所示。

表4 不同整体种子数模型的收敛性

图4 不同整体种子数模型刚度与压缩力关系图

从图 4中可以看出，不同整体种子数模型的刚度仿真结果变化趋势基本相同，即随着施加载荷的增大刚度增大，并且各个模型的刚度仿真数值差距不大。整体种子数为2的模型加载至24 166.3 N时出现不收敛的情况，且不收敛前模型刚度出现明显波动现象。整体种子数为1及1.2的两模型刚度变化基本相同，均在加载至73 000 N左右时出现不收敛现象。两模型在不收敛前刚度同样出现明显波动现象，并且刚度波动较整体种子数为2的模型更加剧烈。整体种子数为1.5的模型为计算收敛模型，但在计算过程中模型多次出现刚度波动情况。总体来说，整体种子数1.5为计算可收敛模型，但结合上述几个模型在不收敛前出现刚度波动的情况，可推断整体种子1.5模型在计算过程中同样存在不收敛倾向，同时也可看出计算模型的收敛性对刚度仿真计算存在很大影响。

2.2 橡胶隔片层数对收敛性影响

基于上述仿真计算结果可知，1.5整体种子数为可收敛模型，选定整体种子数为1.5，改变橡胶和金属层数进行仿真计算，橡胶及金属层数分布情况如表 5所列。各个模型刚度与轴向压缩力的关系如图5所示。

表5 橡胶、金属隔片层数分布

图5 不同橡胶、金属层数模型刚度与压缩力关系图

图5中可以看出，橡胶划分2层模型的仿真刚度明显大于橡胶划分3层模型，说明橡胶网格单元越大仿真刚度越大。当橡胶划分3层时，金属层数为2和3的计算模型均在刚度波动后出现不收敛现象。橡胶3层金属1层及橡胶2层金属2层同为收敛模型，其中橡胶2层金属2层模型在计算过程中的刚度波动明显小于橡胶3层金属1层的模型。根据上述几个模型的计算经验可知，刚度波动处易出现不收敛现象，可以说明橡胶网格单元越大越容易收敛。

3 结 语

综合考虑整体种子数及橡胶金属种子划分层数模型的计算结果，可以看出橡胶网格单元越大越容易收敛。但是橡胶网格单元的增大会导致仿真刚度的增加，因此后续可考虑通过更改调整本构模型参数的方法来实现收敛性和仿真刚度值的统一。另外，整体种子数增大的过程中同样出现仿真不收敛的情况，可见橡胶单元模型的增大也存在临界值，考虑橡胶单元的长宽比同样会影响仿真的计算结果，后续可针对该点进行深入研究。此次研究对于弹性轴承刚度有限元仿真计算过程的准确性与高效性存在指导性意义。