可调拱梁稳定性分析 *

徐锦元，张政武

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

0 引 言

在建筑、交通、水利等领域常见的设备结构中，几乎所有板件、构件与整体结构的受压部位，都会涉及稳定问题，其中钢结构因材料强度高，结构组件纤薄，通常在强度破坏之前便容易发生整体失稳或局部失稳[1]。

国内文献针对拱梁结构稳定性问题的研究对象通常为拱桥或拱坝结构，如邵旭东等[2]提出了一种特大跨径钢-UHPC组合桁式拱桥新体系，并验证了其各施工阶段的稳定性、刚度与强度等使用要求；吕征等[3]以中国某300 m级高拱坝为研究对象，设计了两种方案回填混凝土，然后对两种方案进行了超载能力与稳定性的验证；马坤全等[4]针对铁路拱桥拱梁结合部局部结构的复杂性，建立了精细化模型进行了刚强度分析与稳定性分析；吕君等[5]介绍了拱坝抗剪安全度分析评估方法与整体稳定分析方法及其失稳依据，探讨了拱坝最不利截面抗剪强度指标值；尤吉等[6]提出了一种通透肋式连拱榜山隧道结构，并通过有限元方法对其变形受力特征及结构稳定性进行了分析，证明了设计方案的可行性，为该类隧道结构提供了新思路；李杰等[7]为探究异性拱梁稳定性，利用有限元方法分析了钢箱拱肋板厚、横撑、梁拱刚度对结构稳定性的敏感性；谢肖礼等[8]通过增加刚性斜杆与拱肋及主梁节段形成三角形结构，大幅增加了拱梁固结拱桥整体刚度并增强了其稳定性。而对于非拱桥或拱坝为对象的拱梁结构稳定性研究问题多见于外文文献，如Rawlilson O. Araújo等[9]证明了圆拱形梁振动的数学模型Bresse系统与其渐进稳定性有关，在此基础上模拟了具有记忆效应的拱形梁，建立了外力作用下能量的衰减率；Liu TianQiao等[10]基于最新的弯曲拉挤成型技术，开发了GFRP拱形梁结构，通过对梁的屈曲分析与破坏试验证实了GFRP拱形梁的巨大潜力。

TC4635-Q型钢模台车是一种曲线段可变式钢模台车，可以完成台车4～6 m变高、3～5 m变跨及由变跨引起的变弧，可调拱梁在该台车中负责传递外载荷与增加拱部刚度，并且能够适应不同拱形和跨度范围内拱顶圆弧的调节，其结构的稳定性对于台车整体安全性能十分重要。为探究其稳定性，首先介绍了拱梁结构组成，按照其尺寸参数进行了三维建模，并计算出实际工况下拱梁所承受的外载荷与在外载荷下拱梁的刚、强度，然后将结构强度最不利部位简化为两饺拱计算出屈曲载荷，与通过ANSYS分析整体结构屈曲载荷对比验证了拱梁的稳定性，最后探究了台车跨度变为4 m、5 m与6 m时拱跨、拱高与两千斤支撑间距三组结构参数对可调拱梁整体稳定性的影响，研究结果为拱梁结构的设计与分析提供了一定的理论参考。

1 可调拱梁结构介绍与建模

TC4635-Q型钢模台车主要由模板系统、框架系统与电液系统等组成。框架系统通过伸缩油缸推动横梁外套左右移动实现台车4～6 m变跨，顶升油缸推动台车立柱中套与外套实现3～5 m变高，由变跨引起的变弧通过可调拱梁实现。该钢模台车由两个约6 m长的单元节组成，每个单元节前后两端各有一组、中间均匀分布四组可调拱梁。台车最大跨度为6 m时，一组可调拱梁结构如图1所示。

图1 可调拱梁二维结构1.侧模板 2.拱顶模板 3.固定三角形块 4.可调丝杠 5.可调三角形块 6.连接销轴 7.框架系统 8.纵梁 9.人字千斤

每组可调拱梁由位于中间的一个可调三角形块5与其余若干个固定三角形块3组成，三角形块下端由可调丝杠4连接，上端由连接销轴6首尾铰接，拱顶模板2固定在可调拱梁上表面，两端与侧模板1连接，拱梁两侧通过两组人字千斤9支撑于框架系统7的纵梁8上。由变跨引起拱顶弧度变化时，可调拱梁首先取下可调三角形块，将拱梁分为左右两部分，从两边向中间依次调整丝杠长度并根据实际跨距增减固定三角形块与丝杠数量，直至将整个装置调节至实际位置，完成变弧。

结合图1拱梁二维结构，6 m跨可调拱梁尺寸参数如表1所列。表中：L为拱梁跨度；L1为梁人字千斤支撑间距；L2位拱梁总弧长；H为拱高；h为千斤支撑点与顶点距离；s为拱宽；r为拱梁弧半径。

基于可调拱梁的二维结构与尺寸参数，利用CREO软件建立可调拱梁三维模型，如图2所示。

表1 6 m跨可调拱梁尺寸参数表/m

图2 可调拱梁三维模型

2 拱梁静力学分析

分析可调拱梁稳定性需计算拱梁静力解[1]。可调拱梁材料为Q235钢，其参数如表2所列。

表2 Q235钢材料参数表

可调拱梁所受外载荷来源于拱顶模板，根据规范[11]台车拱顶模板所承受载荷主要包括顶部混凝土自重载荷与局部挤压面载荷。台车在跨度6 m时的实际工况下，拱梁所承受外载荷的计算如表3所列。

表3 可调拱梁外载荷计算公式与结果

将可调拱梁模型导入ANSYS workbench软件进行静力学分析，设置模型材料与划分网格后，根据实际工况下可调拱梁受力情况，将拱梁两端底面与人字千斤底面固定约束，在拱梁上表面施加外载荷P，求解模型得到拱梁位移云图与应力云图如图3所示。

图3 拱梁应力应变云图

由3(a)位移云图可知拱梁最大变形处于拱梁顶端受力处，最大高度降低约1.807 4 mm，小于拱梁最大允许位移[l]=l/1000=6.954 mm(l为拱梁长度)，满足拱梁强度使用要求；由3(b)应力云图可知拱梁结构除去部分应力集中外的整体应力约20.361 MPa，小于材料许用应力215 MPa，满足拱梁刚度使用要求。

3 拱梁稳定性分析

结构稳定性分析理论计算方法一般有针对未变形结构平衡方程的一阶分析法与基于已变形结构几何关系的二阶分析法两种，相应的ANSYS workbench平台提供两种结构稳定性分析模块分别为针对理想物体的特征值屈曲分析与考虑初始缺陷的非线性屈曲分析[1]。

3.1 拱梁屈曲载荷理论计算

由图3拱梁静力学分析结果可知，拱梁结构最危险部位主要处于两组人字千斤支撑之间，将连接相邻两组三角形块的连接看作拱平面外等间距支撑，则弧拱只发生平面内失稳[12]。将两组人字千斤支撑看作弧拱两端，中间部分则为纯压两饺拱，其理论模型如图4所示。

图4 拱梁理论模型

结合《拱形钢结构技术规程》[13]中纯压圆弧两饺拱平面内屈曲载荷计算公式，计算两饺拱矢跨比、拱截面惯性矩以及两饺拱屈曲载荷qcr结果如表4所示。

表4 两饺拱平面内屈曲载荷计算公式与结果

3.2 ANSYS workbench屈曲分析

将外载荷设置为1 MPa的拱梁静力分析结果导入特征值屈曲分析模块[15]，求解得到拱梁模型在理想状态下的一阶屈曲模态云图如图5所示，从云图中可以看出模型屈曲特征值为3.383 9，可知拱梁特征值屈曲载荷为3.383 9 MPa。

设置初始缺陷因子为10%，通过特征值一阶屈曲模态生成含初始缺陷的可调拱梁模型[16]，导入静力学求解模块进行非线性屈曲分析，其中拱梁外载荷设置需大于特征值屈曲载荷[17]，文中设为5 MPa，通过自动迭代131步后，提取出拱梁外载荷迭代值与对应最大位移曲线图如图6所示。

由图6可看出，拱梁模型在外载荷为0～2.95 MPa时，外载荷与位移呈正比，在外载荷增加至2.95 MPa时，拱梁发生屈曲，此时拱梁结构位移达到最大21.59 mm，随着外载荷的继续增大，模型发生失稳。

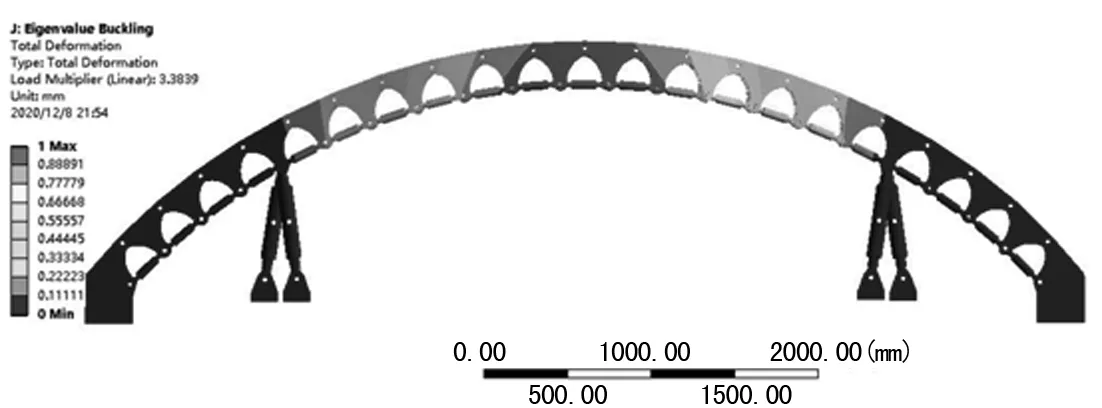
图5 拱梁特征值屈曲位移云图

图6 拱梁外载荷与位移曲线图

由此可知，非线性屈曲分析所得屈曲载荷为2.95 MPa，与特征值屈曲载荷相比小12.8%，显然通过非线性屈曲分析所得屈曲载荷更为精确。

3.3 理论计算与ANSYS分析结果对比

由表4可知，拱梁理论模型即两组人字千斤支撑中间区域计算出的拱梁危险部位屈曲载荷为2.47 MPa，与ANSYS workbench软件非线性屈曲分析计算所得拱梁非线性屈曲载荷2.95 MPa作对比，知两结果相差16.27%，考虑到理论计算模型仅选择两组人字千斤之间部分，且将可调拱梁截面模型近似看作箱型结构，故误差在合理范围之内，验证了软件分析结果的合理性，又由于该分析结果远大于拱梁在实际工况下的外载荷0.0103 MPa，可以证明可调拱梁具有良好的稳定性。

4 拱梁尺寸参数对屈曲载荷敏感分析

在钢模台车变跨时，可调拱梁部分尺寸参数会随之发生变化，为了保证变跨时拱梁的稳定性，选择由部分代替全面而得到全面试验情况的正交试验设计方法，分析拱梁尺寸参数对结构稳定性的影响。研究台车变跨时可调拱梁结构变化，拱梁矢跨比与千斤支撑间距对整体稳定性有较大的影响，选择拱梁跨度、拱高与两组人字千斤间距三组尺寸参数为试验因素，其中拱梁跨度分别为4 m、5 m及6 m时拱高与千斤间距的尺寸作为因素的水平数，得到正交试验因素水平配置如表5所列。

表5 拱梁尺寸参数水平配置表 /m

根据三因素三水平配置表选择正交试验表L9(33)计算[18]，并对结果数据进行分析如表6所列。表中：Ki为该因素在i水平结果的和；ki为对应Ki的均值；R为ki最大值与最小值之差。

表6 L9(33)正交试验计算结果及分析

极差R越大所对应因素越重要[19]，由表6可知，三组因素重要性排序为：拱跨>间距>拱高，并且随着拱梁跨度、间距及拱高的增大，拱梁屈曲载荷逐渐变小，拱梁越不稳定。考虑交互作用影响，避免仿真实验误差，准确检验三组尺寸参数对屈曲载荷影响的显著程度，对表6数据进行方差分析，结果如表7所列。

表7 方差分析结果

F值越大说明因素对结果的影响越大[19]，结合表7分析结果可知，三组结构参数对结构屈曲载荷的影响性排序与表6结果相同。p值小于0.1，则代表该因素与结果存在一定的显著性差异关系[20]，由表7可知，拱跨对屈曲载荷的影响存在一定显著性，拱高与拱宽为非显著因素，对屈曲载荷影响较小。

5 结 语

以可调拱梁为研究对象，为探究其结构稳定问题与影响拱梁结构稳定性的主要因素，首先介绍了可调拱梁主要结构并按照跨度最大6 m的拱梁结构尺寸参数建立了可调拱梁三维模型，之后计算出拱梁在实际工况下的外载荷为0.0103 MPa，对其进行静力学分析，结果说明模型最大变形处于顶部中间，为1.807 4 mm，符合强度使用要求；然后，简化强度最不利区域为纯压圆弧两饺拱，计算出其屈曲载荷为2.47 MPa，并与通过ANSYS软件分析计算出的屈曲载荷2.95 MPa相比误差为16.27%，处于合理范围内，验证出可调拱梁具有良好的稳定性；最后，为探究台车变跨时拱梁尺寸参数对屈曲载荷的影响性，选择拱跨、拱高与两千斤支撑间距三组结构参数作为可变因素，拱梁屈曲载荷为结果，进行三因素三水平正交试验，通过对试验数据分析说明三组结构尺寸参数与屈曲载荷呈负相关，并且其影响性大小排序为：拱跨>千斤间距>拱高，拱跨对结构屈曲载荷的影响存在一定显著性。希望对拱梁结构之后的设计研究有一定的参考价值。