凸显思维过程 落实核心素养——以“函数的奇偶性(一)”教学为例

福建省闽清高级中学 (350800) 陈国鸿

数学概念是数学课堂教学的核心与基础，对培养学生的“四基”、“四能”，提升数学核心素养有着无法替代的作用.概念学习的主要任务就是要引导学生主动参与概念产生、发展的过程，不仅需要知道“是什么”，还应明确“为什么”.章建跃博士说,“概念教学的核心是引导学生开展概括活动，将凝结在数学概念中的数学思维活动打开，以若干典型具体事例为载体，引导学生展开分析各事例的属性、抽象概括共同本质属性、归纳得出数学概念等思维活动而获得概括过程.”[1]因此在数学教学中，教师要从数学概念发生、发展的关键点、学生思维的困惑点、数学核心素养的提升点，设置恰时恰点的问题，激发学生自主参与，使学生真正通过自己的思维，深入理解概念的本质属性，完善认知结构，发展数学核心素养.笔者以新教材《普通高中教科书数学必修第一册(A版)》“函数的奇偶性”(第一课时)教学为例，谈谈在概念教学中引导学生突出思维教学，落实数学核心素养的几点思考.

1 教学案例呈现

1.1 创设数学“内部”情境，引入课题

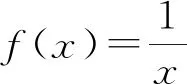
追问1 换一个角度观察这两个函数图象，还有其他的特征吗？

生众：这两个函数图象都具有对称性.

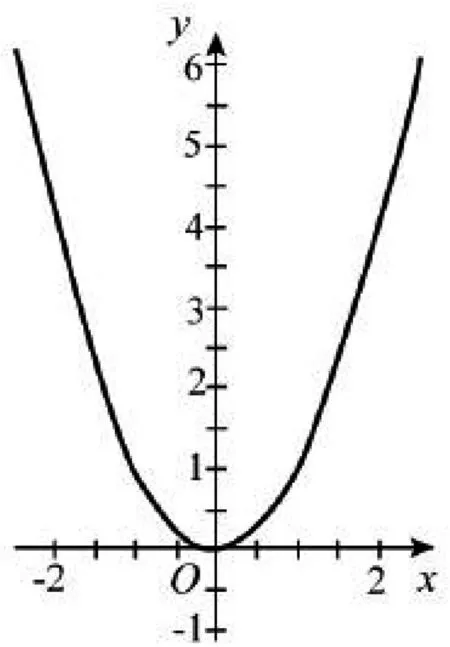
图1

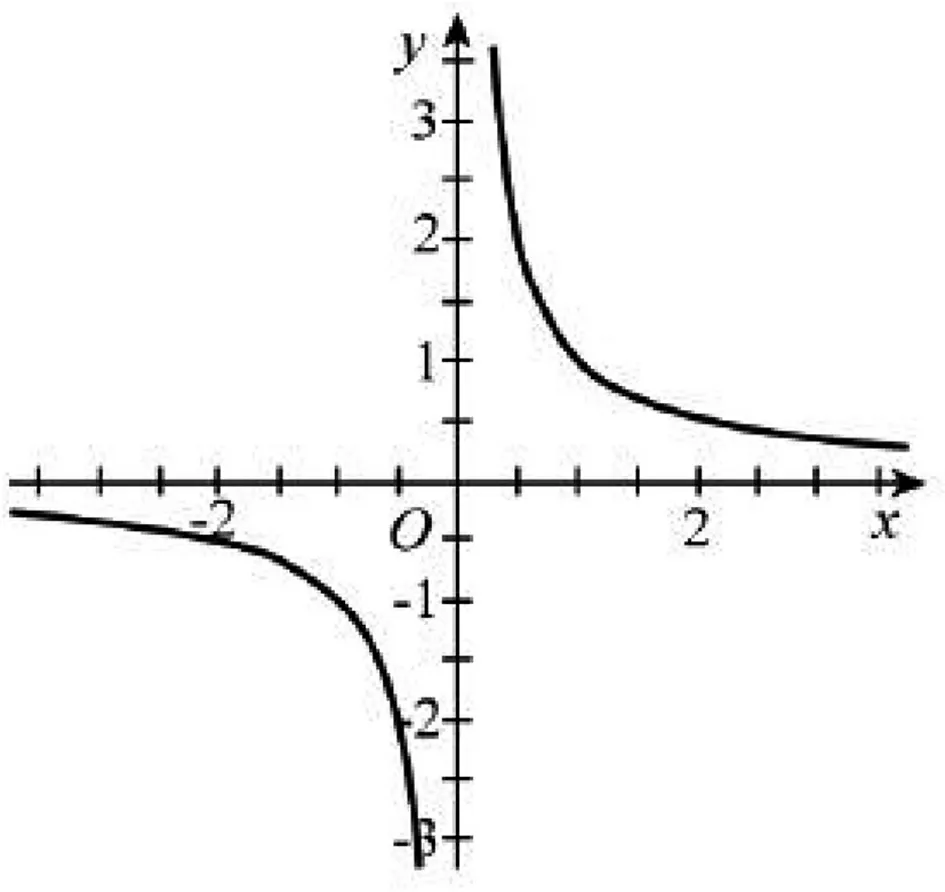
图2

追问2 图1与图2两个函数图象都具有对称性，那么图3和图4这两个函数图象呢？

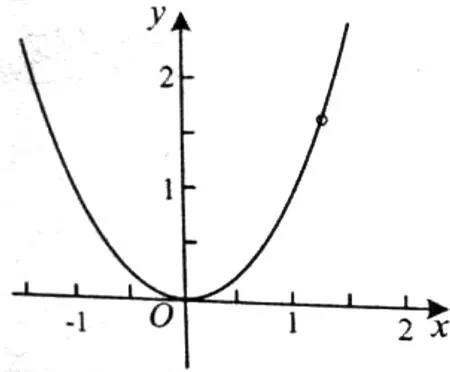
图3

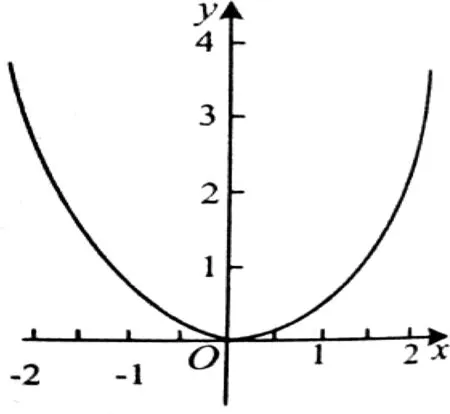
图4

学生发现图3右侧有一个“洞”，不对称.有的学生认为图4对称，有的认为图4也不对称.

教师利用几何画板对图4进行“对折”，证实不对称.

追问3 仅仅通过观察能够准确地判断函数图象的对称性吗？怎样才能精准地刻画函数图象的对称性呢？

设计意图：设置数学“内部”情境，从学生熟悉且具有典型对称性的二次函数与反比例函数图象入手，引导学生用数学的眼光观察、分析；通过反例激发学生的认知冲突，使学生认识到用数量关系刻画对称性的必要性，激发学生的探究欲望.

1.2 从具体到抽象, 催生概念

问题2 请用列表法画出函数f(x)=x2与g(x)=2-|x|的图象,并思考这两个函数图象有哪些共同特征？

生1：它们都关于y轴对称.

生2：我画函数g(x)=2-|x|的图象时，只取了6个特殊点，所以不能肯定g(x)=2-|x|的图象是否会关于y轴对称.

师：你取哪几个点呢？

生2：(1,1),(-1,1)，(2,0),(-2,0)，(3,-1),(-3,-1).

师：你为什么想到取这6个点？

生2：因为点(1,1)和点(-1,1)关于y轴对称，点(2,0)和点(-2,0)，点(3,-1)和点(-3,-1)也分别关于y轴对称.

师：那么应怎样表达出上述这种函数关系呢？

生3：g(-1)=g(1),g(-2)=g(2),g(-3)=g(3).

师：同学们还能找到像这样关系的其它的等式吗？

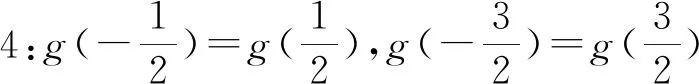
师：能否用符号进行概括呢？

生5：g(-x)=g(x).

师：很好！用变量代替常数.对定义域R中任意的一个x,g(-x)=g(x)都会成立吗?怎样验证这个猜想呢?(学生思考)

生6：对于定义域R中任意一个x，由于g(-x)=2-|-x|=2-|x|=g(x)，因此g(-x)=g(x)成立.

师：生6从代数角度运用函数解析式进行验证，很有见地.我们称这样的函数为偶函数.

问题3 我们知道如果函数f(x)的图象关于y轴对称，那么对于任意的x∈R，函数f(x)满足f(-x)=f(x)；反过来，若对于任意的x∈R，函数f(x)满足f(-x)=f(x)，那么f(x)的图象一定关于y轴对称吗？

生7：如果函数f(x)满足f(-x)=f(x)，在f(x)的图象上任取一点P(x,f(x))，则点P关于y轴的对称点为点P′(-x,f(x)) ，由f(-x)=f(x)得点P′的坐标可以写P′(-x,f(-x)) ，显然该点也在f(x)图象上，故f(x)的图象关于y轴对称.

师：太棒了！因此，“函数图象关于y轴对称”与“对于任意的x∈R，函数f(x)的解析式满足f(-x)=f(x)”等价.对于这种函数，大家知道定义域有什么特点吗？

生众：函数f(x)的定义域关于原点对称.

问题4 请从“数”的角度给出偶函数的定义.

(师生共同归纳偶函数的定义)

问题5 类比偶函数的定义，同学们能给出奇函数的定义吗？

设计意图：从数与形两个角度对偶函数进行刻画，引导学生在自身实践体会的基础上，抽象概括出偶函数概念，体验数学知识鲜活的“生长性”，培养学生抽象概括能力.

1.3 数学运用，深化理解

例1 判断下列函数的奇偶性：

设计意图：巩固奇(偶)函数概念，并引导学生从例1归纳得到：由函数的奇偶性可把函数分为四类.

问题6 大家能归纳出判断函数奇偶性需要几个步骤吗？

例2 (1)判断函数f(x)=x3+x的奇偶性；(2)图5是f(x)=x3+x的一部分图象，你能根据f(x)的奇偶性将图象补充完整吗？

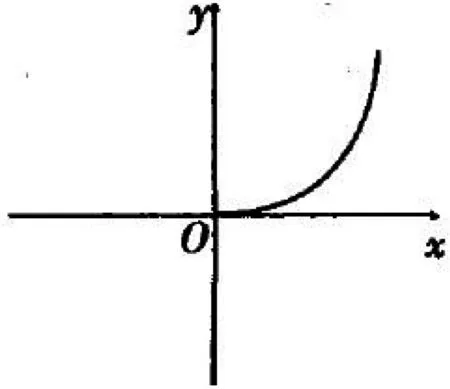
图5

拓展对于函数f(x)=x3+x，是否可以通过添加某些项，使得f(x)=x3+x仍是奇函数呢？既是奇函数也是偶函数？既不是奇函数也不是偶函数？

设计意图：学生并不熟悉函数f(x)=x3+x的图象，通过拓展，引导学生从解析式入手,探求f(-x)与f(x)的关系,利用定义进行判断，深化对函数奇偶性概念的理解.

1.4 总结反思，提升高度

问题7 回顾本节课的学习过程，我们是如何对函数奇偶性进行研究的？

问题8 大家对偶函数和奇函数的特征有那些认识？能总结出偶函数和奇函数的相同点和不同点吗？

问题9 如果奇(偶)函数在(0,+∞)单调递增，同学们可以得到它在(-∞,0)上的单调性吗？

设计意图：引导学生对本节课所学的内容进行反思，比较偶函数和奇函数的异同，领悟函数的奇偶性在研究问题中的作用，在总结反思中提升学生的思维高度.这样，学生收获的不仅仅是一个定义，而要深远得多.

2 教学反思

2.1 精心设置问题串，孕育核心素养

“问题串”是指教师立足概念建构的逻辑性，围绕课堂教学目标精心设置的一组驱动性问题.恰当的设问，能更简洁有效地驱动数学教学过程，激发学习兴趣、启迪思维.因此，在课堂教学中，教师应深入挖掘数学教材中隐性的精神价值和营养成分，依据学生学习的“最近发展区”原理，创设思维含量高、指向性明确的驱动性问题，使这些问题成为引发学生思考的诱因，成为课堂有效生成的驱动力.这对于形成系统的数学思维方式，提升数学核心素养有着重要作用.本课例立足概念建构的逻辑性，以初中已学过的图形对称为载体，从学生熟悉的几个特殊函数入手，精心设计层次清晰的递进式问题串，顺应学生的思维发展，循序渐进地展开探究，层层深入.在引导学生主体参与中，让动手操作、动脑思维和语言表达有机结合，引导学生经历概念的引入、生成、应用与反思等阶段.通过亲身体验，学生不仅品尝到了“发现”的乐趣，而且理清了“函数奇偶性”概念的本质属性，优化了思维品质，实现了“低起点，高落点”的教学目标.

2.2 凸显思维过程，培养核心素养

数学概念的产生和发展是一个数形结合的思维过程，是将数学概念中凝结的数学家的思维活动打开，借助若干典型实例，通过观察、比较、抽象、概括等思维活动，亲历数学概念的发现、抽象和概括过程.因此概念教学应通过学习活动，突出学生的思维过程，启发学生 “想什么” “怎么想”，让学生经历从自然语言、图形语言到符号语言的“数学化”过程，也是一个将函数图象数量化的思维过程，从理解、感悟到“再创造”的过程中实现深度学习.本课例有效设计学生的思维活动，激发学生的认知冲突.通过不断追问，引导学生从“数”角度思考，构建出函数模型f(-x)=f(x)，将图象的对称性问题转化为函数的数量关系问题，并逐步将学生的思维引向深入，引导学生从代数角度给出严格证明，完成对“函数奇偶性”概念的建构.这样的概念生成过程是自然而鲜活的，还原了“春风化雨、润物无声”的本来面目.在数学应用环节，通过问题与拓展，让学生通过添加项，构造不同的函数，学生通过思维的交锋与碰撞，加速了概念的内化，发展了直观想象、数学抽象、逻辑推理、数学建模等核心素养.

2.3 重视总结反思，生长核心素养

课堂总结并非是让学生简单地复述本节课内容，而是引导学生对所学习的知识进行反思，加深学生对知识的内化和掌握、对数学思想方法的认识与感悟，使学生能运用数学思想方法分析和解决数学问题，并提炼出研究相关问题的一般方法.本课例通过三个明确的问题，引导学生对函数奇偶性的研究过程进行总结反思，并引导学生深入思考函数的单调性与函数的奇偶性之间的联系、总结研究函数性质的一般方法；使学生能够建立起对函数的整体性认识，并体会到利用函数的奇偶性，可收到“事半功倍”之功效，从而深刻体会研究“函数奇偶性”的必要性.学生在总结反思中，知识与能力自然迁移，从“见山是山”的浅层认识提升到“山外有山”的境界，思维向更高层次发展，数学核心素养得以落地生根.

数学核心素养的培养是一个循序渐进的过程，是学生在学习过程中逐步形成与发展的.在概念教学中，教师应精心组织课堂教学活动，打造“重亲身体验、重思维参与、重知识建构”的活力课堂，为学生的学习提供“支点”与“脚手架”，引领他们在探究活动中有效提升思维深度与解决问题的能力，从而让数学核心素养落地生根.