从一道模拟题谈新高考下二面角的解题教学

江苏省丰县中学 (221700) 缪苇伟

立体几何是高中数学中非常重要的一部分内容，也是高考数学重点考查内容之一. 通过对立体几何的学习，可以培养学生的空间想象能力和逻辑推理论证能力. 2020年高考数学全国共有13份试卷，每份试卷对立体几何内容都进行了考查，尤其是二面角的考查较为突出，以学生所熟知的立体几何体为载体，考查学生对二面角定义的理解及其二面角的求法，进而考查学生严谨的逻辑推理能力和运算求解能力.

本文结合徐州市2020高三期中一道模拟题，谈谈对立体几何中二面角的备考，进而把握好立体几何的教学，更好的体现数学的核心素养.

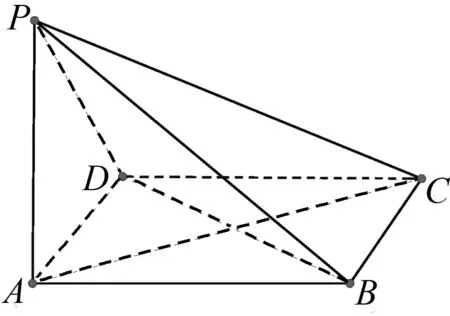
图1

题目如图1，在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥平面ABCD.

(1)求证：平面PAC⊥平面PBD；

(2)若PA=AB=2,∠BAD=60°，求二面角A-PB-D的余弦值.

一、知识再现

1. 二面角的定义

平面内一条直线把这个平面分成两部分，其中的每一部分叫做半平面，当其中一个半平面绕着这条直线旋转时，两个半平面就形成了“角度”.一般地，一条直线和由这条直线出发的两个半平面所组成的图形叫作二面角，这条直线叫做二面角的棱，每个半平面叫做二面角的面.

在《必修二》中，二面角的大小是通过二面角的平面角来刻画的.一般地，以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的射线，这两条射线所成的角叫做二面角的平面角 ，其范围为[0,π] .

2. 空间向量与二面角

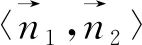
图2

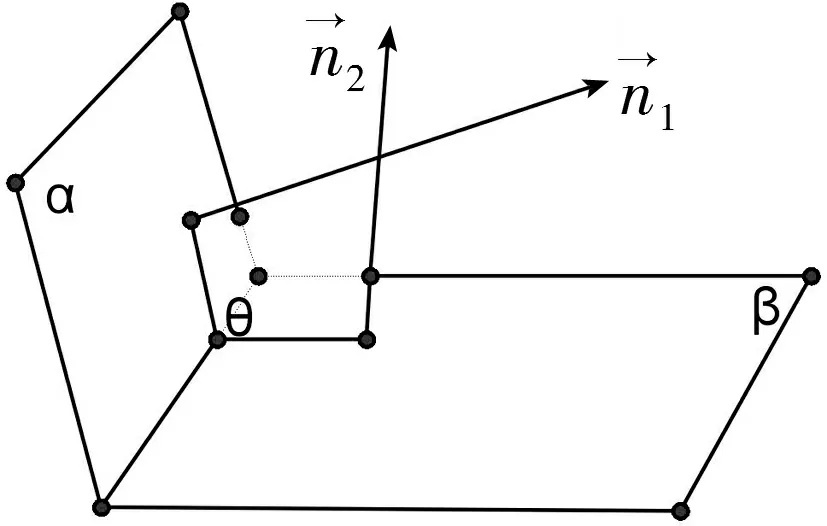
图3

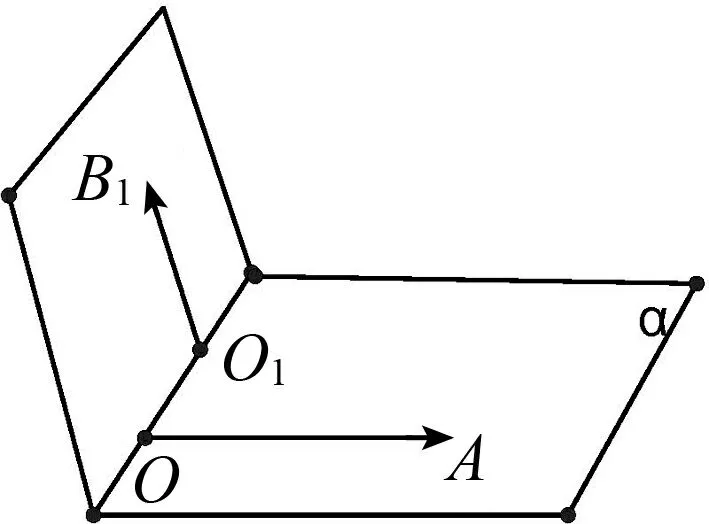
图4

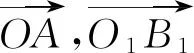
三、备考策略

1. 借助二面角的平面角来求解

把空间角转化为平面角来研究是求解空间角的大小常用方法，在二面角的平面角定义中，由于O点的选取不改变角的大小(等角定理)，因此对于O点的定位是解题的关键所在.一般的，选取O点常用如下两种方式：

①定义法(以算定位)

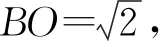
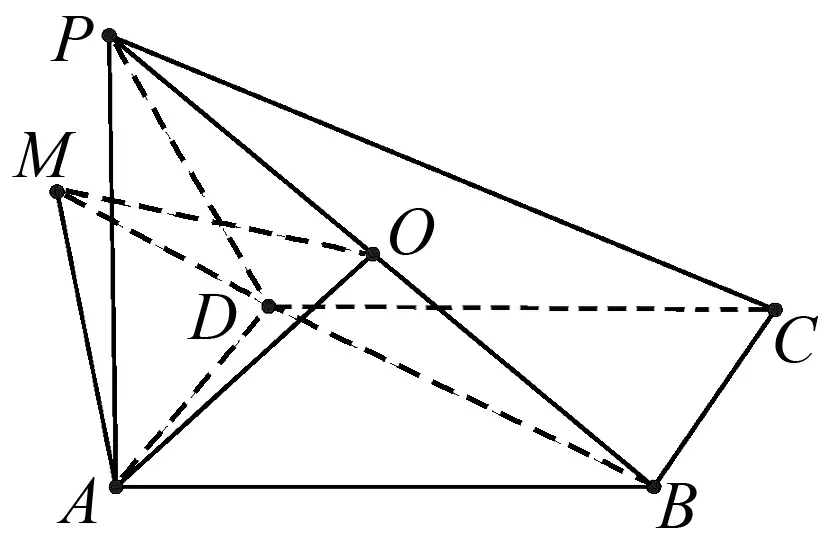
图5

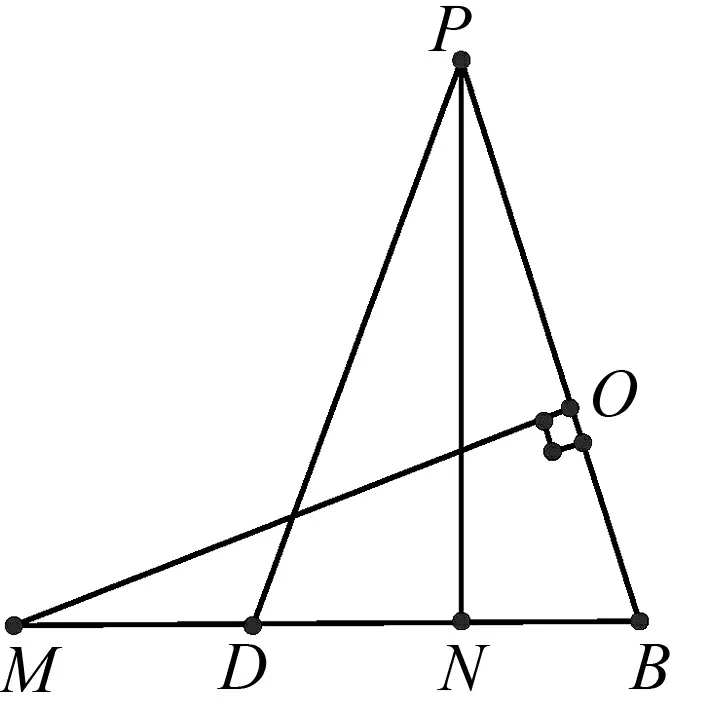
图6

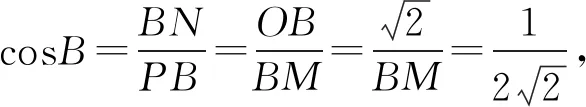
②三垂线法(先找其中一个半面平的一条垂线，再一作一连)

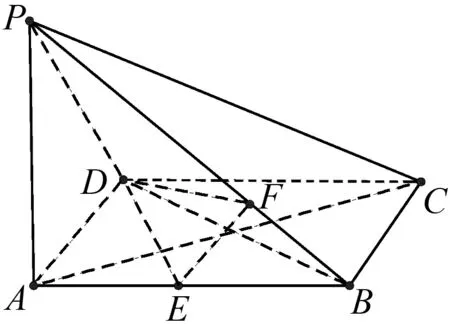
图7

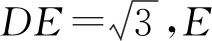
2. 借助空间向量来求解

利用空间向量来解决二面角问题，通常有两种方式：一种是借助公共棱的垂线所在直线的方向向量的夹角来刻画，另一种是借助半平面的法向量的夹角来刻画.解决问题的关键是通过向量的坐标运算来求解.

③求公共棱的垂线所在直线的方向向量的夹角(基底法)

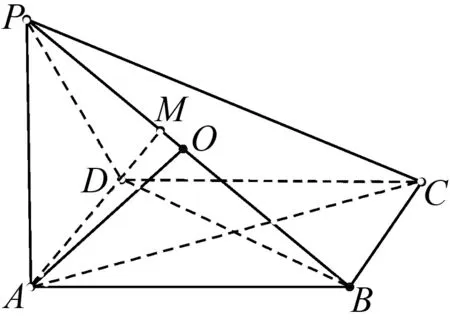
图8

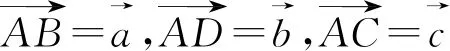
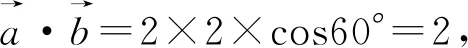
④求法向量的夹角(坐标法)

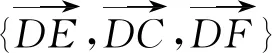
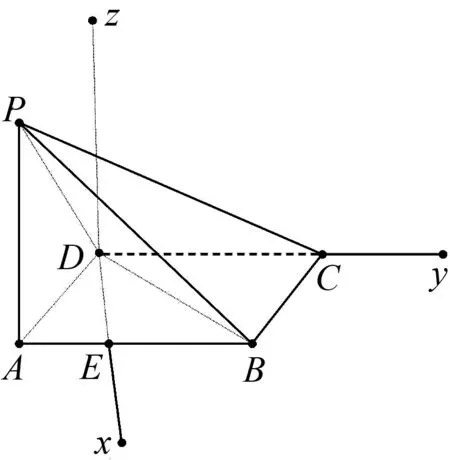
图9

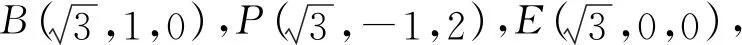
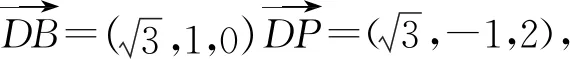
2020年高考立体几何试题几乎都能在教材上找到原型，体现了高考命题回归教材、贴近高中数学教学的改革思路，进而以教材为本，发展数学思维，促进学生对数学本质的理解；同时，2020年高考立体几何试题中考查的几何体基本都能直接建立空间直角坐标系进行求解，凸显了向量在解决立体几何问题中的重要作用，引导学生平时注重对通性通法的训练. 另外，在计算的问题上，要求学生能在空间和平面之间相互转化，简化问题，综合考查学生的思维水平.