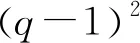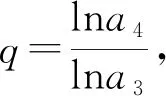基于切线不等式背景下的一类数列放缩问题

浙江省杭州市源清中学 (310015) 王 凯

在人教版A版选修2-2教材第一章《导数及其应用》第1.3节《导数在研究函数中的应用》的配套练习B组第一题的第三小题是研究一个指数不等关系，问题如下：

利用函数的单调性，证明不等式ex>1+x,x≠0，并通过函数图象直观验证.

通过构造函数，借助导数工具，这个问题不难解决.我们可以验证函数f(x)=ex在(0,1)点的切线就是g(x)=x+1(如图1)，所以结论可以进一步变成ex≥1+x(x∈R)，我们这里把它叫做第一切线不等式.当x>-1时，不等式两边同时取自然对数可得x≥ln(1+x)，此时将不等式中的x用x-1替换掉后可得一个关于自然对数的不等关系lnx≤x-1(x>0)，我们同样可以验证函数f(x)=lnx在(1,0)点的切线就是g(x)=x-1(如图2)，我们这里称其为第二切线不等式.以下我们就基于这两个切线不等式来解决一类数列的放缩问题.

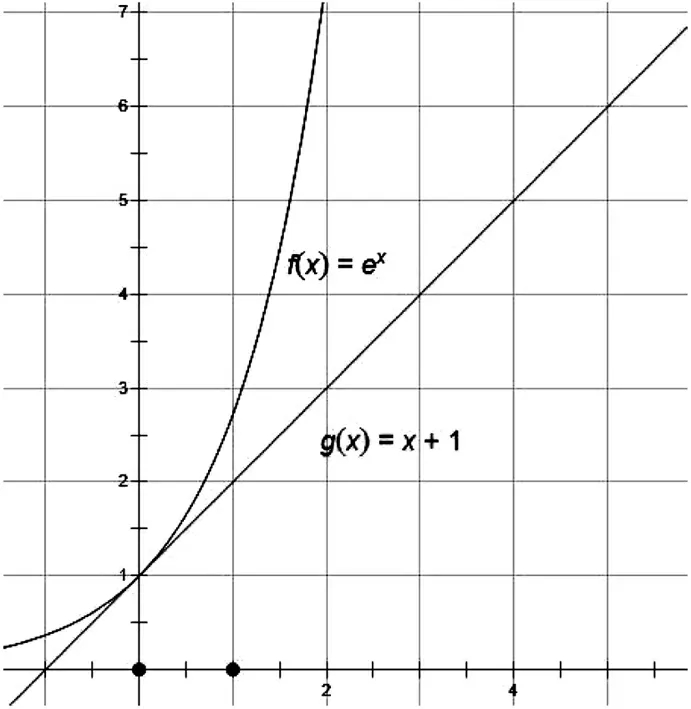
图1

例1 已知数列{an}中，a1,a2,a3,a4成等差数列，且3a1-a2+a3+1=ea2+a3-a4.若a2<0，则( ).

A.|a1|>|a2|且|a3|>|a4|

B.|a1|>|a2|且|a3|<|a4|

C.|a1|<|a2|且|a3|>|a4|

D.|a1|<|a2|且|a3|<|a4|

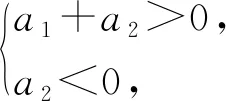
如果我们不用第一切线不等式，也可以通过构造函数，用导数来探究目标函数的单调性，进而找到不等关系解决问题.但这个过程就会比较繁杂臃肿，小题大做也会降低解题的效率.下面我们来看2018年浙江省高考卷选择题的压轴题.

例2 已知a1，a2，a3，a4成等比数列，且a1+a2+a3+a4=ln(a1+a2+a3)，若a1>1，则( ).

A.a1a3，a2

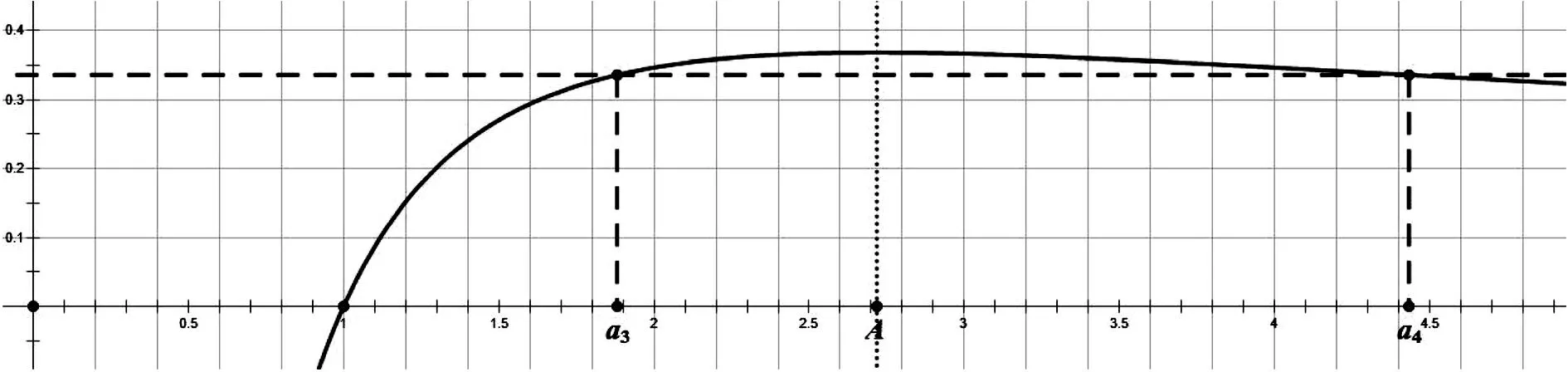
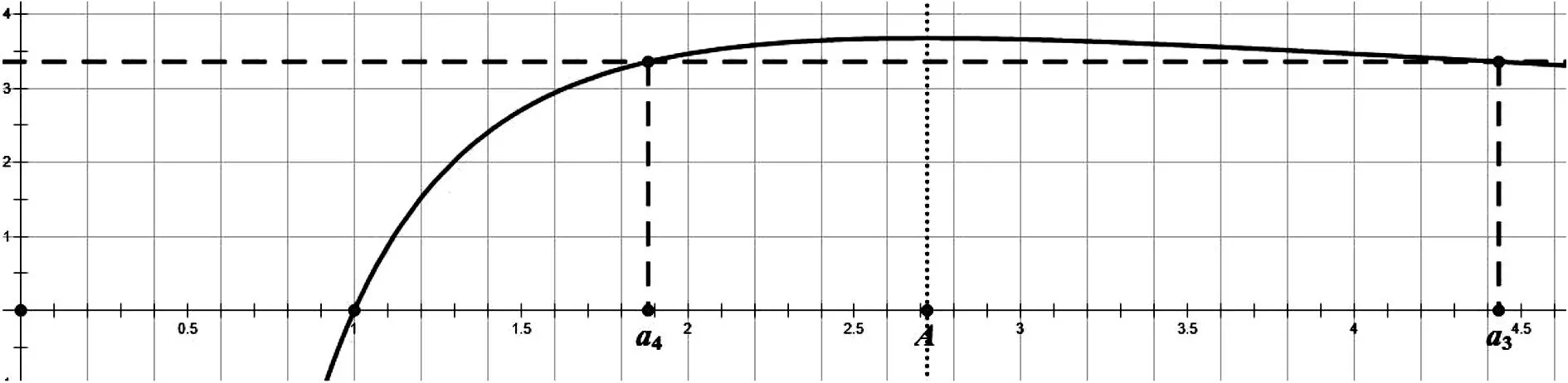
C.a1a4D.a1>a3，a2>a4

解析：由第二切线不等式可得a1+a2+a3+a4=ln(a1+a2+a3)≤a1+a2+a3-1，所以a4≤-1，即a1q3≤-1，可得q<0.选项要我们判断a1、a3和a2、a4的大小关系，即考察这个等比数列奇数项和偶数项的单调性，本质上就是判断判断q和-1的大小关系.若当q<-1时，a1+a2+a3+a4=a1(1+q)+a1q2(1+q)<0，而a1+a2+a3=a1(1+q+q2)=a1[1+q(1+q)]>a1>1，即ln(a1+a2+a3)>0，此时a1+a2+a3+a4≠ln(a1+a2+a3)，所以这种情况不成立，故q∈(-1,0)，那么有a1-a3=a1(1-q2)>0，即a1>a3，同理a2>a4.所以答案为B.

这个问题借助第二切线不等式去掉对数符号后，通过选项的提示让我们明确了问题解决的方向.这样一道高考选择压轴题能被我们轻而易举的拿下，下面我们再来看一个例子.

例3 (浙江省绍兴市上虞区2019年高三二模)已知数列{an}是公比为q(q≠±1)的等比数列，且a1>0，则下列叙述中错误的是( ).

A．若a2+a4=lna1+lna3，则q<1.

B．若a2+a3=ea1+ea4，则q<-1.

C．若a1ea2=a3ea4，则(a2+1)(q+1)<0.

D．若a1lna4=a2lna3，则(a3-e)(q-1)>0.

先不妨假设a31，所以q-1>0.所以结论为(a3-e)(q-1)<0.

图3

若a3>a4(如图4)，那么有a3>e得到a3-e>0.此时又有a3>a4得到q<1，所以q-1<0.结论同样为(a3-e)(q-1)<0.故D选项的说法不成立.

图4

这类问题的一个基本特质是含有自然指数和对数的结构，最终的目的是要确定一种不等关系.此时我们可以尝试一下这类源于课本的切线不等式，我们只需要一步简单的放缩，接下通过代数运算可以帮我们快速的解决这类数列中的不等关系，所以在高三的复习教学中要给予足够的重视.