基于核心素养评价框架的试题命制研究*
——以函数综合题的命制为例
福建省莆田第十中学 (351100) 黄启贤
基于数学学科核心素养的命题应具备以下环节:构建学科核心素养的评价框架;依据评价框架编制基于核心素养的试题;给出评分标准及相应的核心素养的水平划分依据[1].
1 构建评价框架
以高考命题的要求:“基础性、综合性、应用性、创新性[2]”为标准,以数学核心素养的水平划分为基础,将知识学习的过程划分为三个阶段,构建如表1所示的核心素养评价框架.

表1 核心素养评价框架
核心素养水平一是高中毕业应达到的要求,也是知识学习过程中的知识理解阶段.主要是指在熟悉的情境中,选择合适的定理、性质等解决一些简单的相似的问题,感悟过程中的通性通法,形成良好的思维品质,会用数学直观来有条理地解释实际情景中与数学相关的问题.
核心素养水平二是高考应达到的要求,也是知识学习过程中的知识迁移阶段.主要是指在关联的情境中,选用合适的定理、性质,设计合理运算程序,构建恰当的数学模型等解决一些较为复杂的问题,感悟概念、命题、定理之间的内在逻辑,理解数学思想方法,形成规范化思考问题的品质,会用模型的思想阐释生活中的随机现象.
核心素养水平三是针对部分必修或选择性必修的内容提出的要求,也是知识学习过程中的知识创新阶段.主要是指在综合的情境中,发现数学研究对象,能在结论的基础上形成新的命题,能对复杂问题,构建过渡性命题,建立恰当的数学模型来解决问题.感悟数学原理,会用数学原理阐释生活现象.
2 编制基于核心素养的试题
试题能够启发学生在日常生活中发现数学,学习数学,引导学生主动思考,进而提高学习兴趣和解决实际问题的能力[4].基于核心素养的试题命制,围绕数学内容主线,关注知识、方法、素养的落实与比重分布,合理设置试题普适性与区分度.文章以一道函数综合题的命制过程为例,展示基于数学学科核心素养的试题命制过程.
2.1 意图分析
《中国高考评价体系》通过“一核”“四层”“四翼”6个字高度概括了试题命制的目的、内容及要求,提出了命题理念从“知识立意”“能力立意”向“价值引领、素养导向、能力为重、知识为基”的转变[2].高考的评价体系下的函数综合题的命制应遵循以下几个方面.从考查目的看,问题的设计应允许多角度作答,引导学生从“解题”到“解决问题”的转变.从考查内容看,试题以指、对、幂函数与三角函数的组合运算为载体,检测函数的图象与性质的深入理解与综合应用等必备知识,要求学生灵活应用各种数学思想方法来解题,同时也考查学生的数学学科素养.从考查要求看,函数综合题置于压轴题的位置,体现试卷的效度与区分度,强调知识的应用与创新,其中分值安排为:基础性约占30%,综合性约占30%,应用性与创新性约占40%.
2.2 素材选取
函数综合题多由指数型函数、对数型函数、幂函数型函数、三角函数的运算或复合得到的,考查函数的单调区间、最值、极值、零点等性质及其应用.由于三角函数所特有的有界性与周期性,使得三角函数与其他函数相结合为载体的试题中,在考察性质或应用时,需用到放缩比较、估值分析、周期讨论等,有较强的综合性和创新性.拟选用三角函数与对数型函数组合的形式作为试题载体,取2019年全国理数I卷20题以函数f(x)=sinx-ln(1+x)为素材.
2.3 试题初拟
在2019年试题中,所选用的函数是三角函数与对数型函数组合的形式,故试题有以下改编设想.将sinx改变为asinx+bcosx,或axsinx,或axcosx,将ln(1+x)改变为aln(b+x),或aex+b,或ax2+bx+c,或几个的组合.第一问设定为求单调区间或值域等相关问题.第二问设定为判断或求极值点、或零点相关的问题.在问题的设计上,考虑到学生思维的整体性、连贯性、递进性,在难度与知识的关联度上逐层推进、逐步提高.在第二问中要求学生构建过渡性命题,构造运算程序,抓住问题的本质,以解决问题,体现命题的选拔功能.
首先,尝试将sinx改为acosx,即f(x)=acosx-ln(1+x).当a<0时,f(x)的图象如图1所示(取a=-2),当a>0时,f(x)的图象如图2所示(取a=2).初步探究其知识点、蕴含的学科素养等,可知基本上与原题重叠,解题思维、解题方法与原题基本一致,故不予选用.

图1 图2
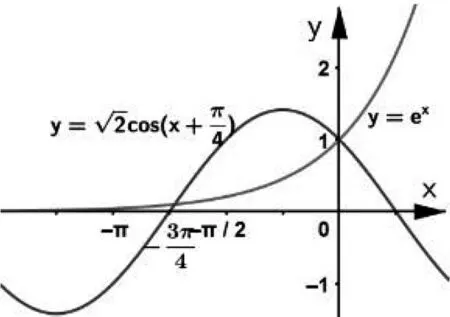
进一步设想,将f(x)=sinx-ln(1+x)中的ln(1+x)改为aex,即f(x)=sinx-aex.当a=1时其图象如图3所示.此时可设计第一问:当x≥0时,f(x)≤-1.尝试证明验证:f′(x)=cosx-ex,∵当x≥0时,cosx≤1,ex≥1,∴当x≥0时,f′(x)=cosx-ex≤0,∴f(x)在[0,+∞)上递减,∴f(x)≤f(0)=-1.如图4,观察y=sinx与y=ex的图象的关联度以及从设问的验证过程,可以看出虽然题目的切入点低,但条件的约束性可进一步加强.

图3 图4
考虑到y=xex过原点,尝试将ex替换为xex.观测图5中的y=sinx与y=xex的图象,以及图6中函数f(x)=sinx-xex的图象特征,初步能达到预期目标.
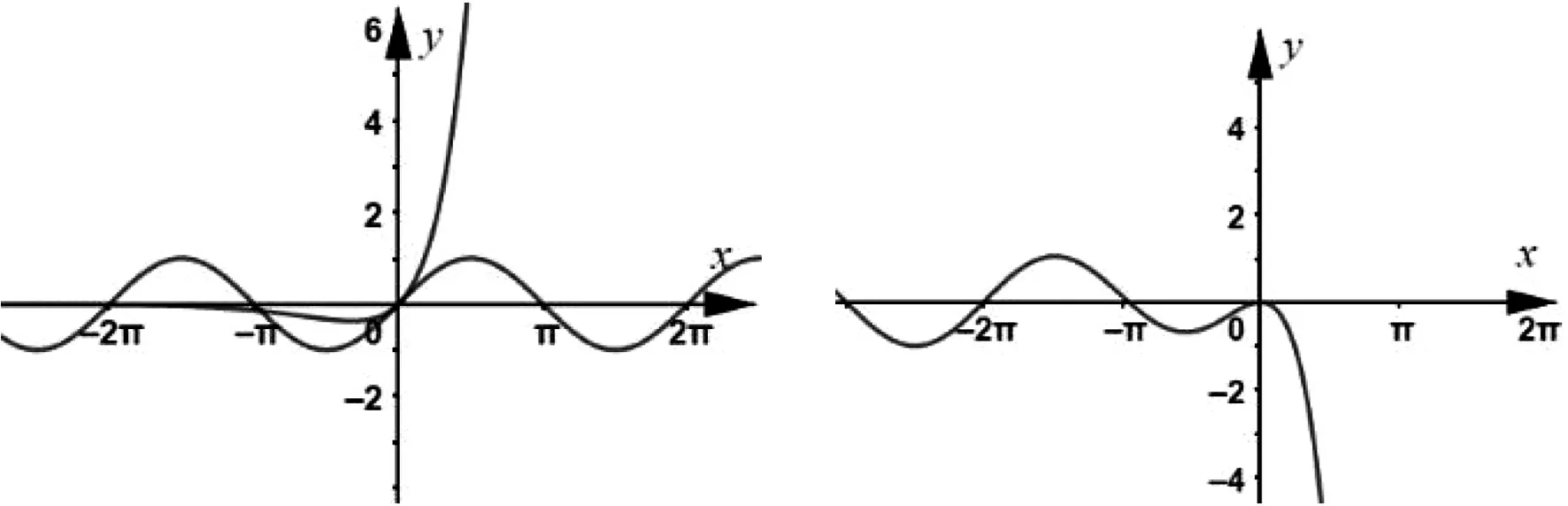
图5 图6
当x≥0时,y=sinx与y=xex两图象恰有公共点为O(0,0),且当x∈[0,+∞)时,y=xex的图象始终在y=sinx的上方.当x∈(-∞,0)时,y=xex的图象在x轴的下方.观察图象可知,y=sinx与y=xex的交点落在((2k-1)π,2kπ),k∈Z且k≤0上,且每个区间有2个零点.依据命题预设,初拟试题如下:已知函数f(x)=sinx-xex,证明:(1)当x≥0时,f(x)≤0;(2)当-π 对初拟试题第(1)问的尝试证明可知,题干中的函数改为f(x)=sinx-xex之后,试题的切入点没有显著提升,但考查的角度、考查的知识点更丰富,蕴含的思想方法更多样性,其中包含了导数运算法则的使用、三角函数的有界性、(x+1)ex≥ex≥1的放缩运算、单调区间的判断、根据单调性求值域等. (1)解法1:∵当x≥0时,cosx≤1,(x+1)ex≥ex≥1,∴当x≥0时,f′(x)=cosx-(x+1)ex≤0,∴f(x)在[0,+∞)上递减,∴f(x)≤f(0)=0.命题得证. 解法2:∵当x≥0时,ex≥1,∴-xex≤-x,∴sinx-xex≤sinx-x.设g(x)=sinx-x(x≥0),g′(x)=cosx-1≤0,∴g(x)在[0,+∞)上递减, ∴g(x)=sinx-x≤g(0)=0,∴当x≥0时,f(x)=sinx-xex≤0.命题得证. (2)解法1:f′(x)=cosx-(x+1)ex,f″(x)=-sinx-(x+2)ex. 综上,当-π 图7 以下从试题参数的引入、知识的交汇、以及命题的等价转换等方面可对试题作拓展研究. 拓展1(引入参数探究)已知函数f(x)=sinx-axex,(1)若a=1,证明:当x≥0时,f(x)≤0;(2)当-π 拓展2(与数列交汇命题)已知函数f(x)=sinx-xex,证明:(1)当x≥0时,f(x)≤0;(2)f(x)在(-∞,0)上的零点从大到小排列为:a1,a2,…,an,…,求使得|a1|+|a2|+…+|ak|<100π成立的k的最大值. 该题是函数综合题,是数学试卷中的压轴题,属于知识综合运用的题目,借助数学软件GeoGebra实验探究,将指数型函数与三角函数巧妙结合考查函数恒成立及零点问题.在数学对象的数学运算过程中考查学生新数学情景下知识迁移、知识创新能力.两步的分值分别设定为5分、7分. 第(1)问是探究函数的最值问题.解法一是借助求导法判断函数的单调性,再其利用比较大小,其间用到了放缩(x+1)ex≥ex≥1、引入中间值等.解法二是用分析法,先以放缩法得到sinx-xex≤sinx-x,再结合单调性的应用得最值,属于知识迁移层面.体现了学科的基础性与综合性,其涉及的核心素养水平划分为L2、I2、O2. 从逻辑推理素养方面看,涉及到函数y=ex,y=xex,y=sinx的图象与性质的理解,并利用其性质进行论证.如果论证途径清晰,推理过程表述严谨,根据加分原则,可以认为达到L2的要求,得2分.从直观想象素养方面看,导数与单调性的转化,单调性的图形表示,要求学生明确代数与几何的关联,并依此解决问题.如果函数与图形转换合理,问题得以解决,根据加分原则,可以认为达到I2的要求,得1分.从数学运算素养方面看,涉及到导数的运算,三角函数的有界性,(x+1)ex≥ex≥1的放缩运算,单调区间的判断,根据单调性求值域等.此处若运算过程合理,结论正确,根据加分原则,认为达到O2的要求,得2分. 第(2)问是探究函数零点的存在性问题,学生在经历第(1)问的基础上,对函数有了从数到形,从抽象到直观的认识,属于知识创新层面.体现了知识的综合性与创新性.其涉及的核心素养水平划分为A3、L3、I3、O2. 从数学抽象素养方面看,由于三角函数与y=(x+n)ex,n∈N+的单调区间不同,需要分类讨论.若能分类合理,讨论严谨当,抽象合理,根据加分原则,可以认为达到A3的要求,得2分.从逻辑推理素养方面看,要求能够将二次导函数作为过渡性命题,再回到一节导函数,最后到原函数的探讨上,进而解决问题.如果命题构建合理,推理过程严谨,结论符合预期,根据加分原则,可以认为达到L3的要求,得2分.从直观想象素养方面看,要求能够将零点问题转化为交点问题,结合零点存在定理实现数形之间的转换,形成解决问题的思路.如果数形转换合理,目标达成,根据加分原则,可以认为达到I3的要求,得1分.从数学运算素养方面看,要求能够结合三角函数的单调区间分布特点,对现有函数的区间作尝试性分段探讨,在运算过程能根据需要引入二阶导数,进而解决问题,根据运算结果判断单调性,进而求得最值,认为O2的要求,得2分.2.4 试题打磨

2.5 解法探究
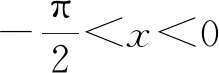

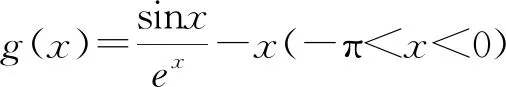
2.6 试题拓展

3 评分标准及核心素养的水平划分
3.1 第(1)问的核心素养水平划分
3.2 第(2)问的核心素养水平划分

