共点旋转直线斜率问题的简化策略*

福建省泉州第一中学 (362000) 张国川 任晓红

最近笔者所在学校举行数学周练，一道解析几何题目学生做得并不理想，原因在于学生初学椭圆，对于坐标法解决几何问题的方法还不熟悉；其次对于繁琐的数学计算处理不当导致计算错误，也有不懂得如何简化复杂的式子变形以致出现解题瓶颈，无法得到想要的结果.解析几何重在考查学生数学运算的核心素养，但倘若不能选择合适的简化运算方法，光有“埋头苦算”的数学精神还远远不够，在算的路上除了低头苦算也得时常抬头“仰望星空”，寻找最恰当的运算技巧，实现简化运算的目的.本文就该题的解答给出四种简化运算办法，只为抛砖引玉给同学们指路.

(1)求动点P的轨迹方程E.

(2)若A是轨迹E的左顶点，过点D(-3,8)的直线l与轨迹E交于B,C两点，求证：直线AB,AC的斜率之和为定值.

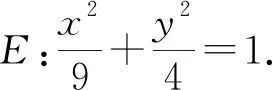
(2)策略1：韦达定理+整体代换

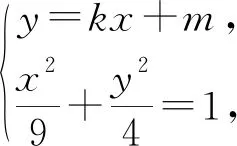
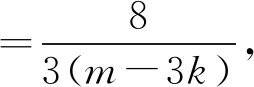
策略2：仿射变换+韦达定理

策略3：变换顺序+齐次化变形

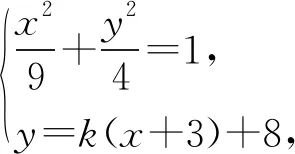
策略4：曲线退化+另类双联立

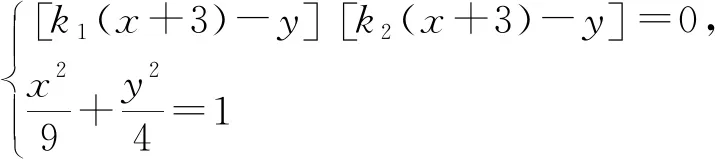
本试题是一类典型的“动直线斜率和或斜率积”求解问题，研究两根和与积时常可以联想到韦达定理，作为简化运算的策略，策略1中韦达定理发挥的作用是整体代入，采用设而不求简化运算.但本题式子计算并不简洁，为了解决斜率和通分后式子较复杂，考虑建立仿射变换在新坐标系下研究该问题，由于是整体平移因此不影响图形之间的位置关系，故而结果依然不会发生改变.策略2正是基于此对策略1进行改进得到优化解法.

策略1和策略2是基于方程联立，韦达定理整体代换求出斜率和，策略3则是变换解题顺序，先通过齐次化变形构造出两动直线的斜率模型，把两条直线的斜率转化成一元二次方程的根，最后再利用韦达定理求解，实现简化运算的目的.策略4是以高观点俯视试题，以二次曲线理论为基础，研究退化的二次曲线，采用交轨法思想引领，通过退化曲线与椭圆的轨迹交点构造出直线BC的方程，已知直线BC过点D(-3,8)，可化归成含参直线过定点问题，参数k1,k2的和就可轻松求出.综上所述，韦达定理整体代换、仿射变换、齐次化变形和交轨法是简化解析几何斜率和(积)求解的四种有效策略.