优化指标一致的滚动轴承故障复合诊断方法

张 龙，蔡秉桓，熊国良，胡俊锋

(1.华东交通大学 机电与车辆工程学院，南昌 330013；2.中国铁路南昌局集团有限公司科学技术研究所，南昌 330002)

滚动轴承广泛应用于机械、交通、航空航天等领域，是旋转机械的重要零部件之一。但由于工作环境恶劣，易发生故障，若未及时发现则可能引起严重后果。因此，准确判断滚动轴承健康状态尤其是诊断早期故障，对于提高机械设备的可靠性、可用性和保障设备安全运行至关重要[1-2]。然而早期故障引起的冲击特征非常微弱，同时受传递路径、噪声和偶然性冲击干扰等因素的影响，早期故障诊断并非易事。

传感器采集到的振动信号是轴承故障引起的冲击力与轴承和轴承座等构成的系统的传递函数卷积结果。为了消除系统传递路径的影响，文献[3-6]采用最小熵解卷(minimum entropy deconvolution,MED)消除传递路径影响，并通过包络谱分析实现故障诊断。然而MED中以最大峭度替代最小熵，由于峭度不能考虑轴承故障冲击的周期发生特点，当信号中出现外界偶然性干扰冲击时，MED解卷积结果不甚理想。考虑到轴承故障特征信号从冲击部位到传感器的传递路径影响，同时为了充分衡量信号中连续的周期性冲击成分，胡爱军等将谱峭度与最大相关峭度解卷积(maximum correlated kurtosis deconvolution,MCKD)相结合，旨在得到周期性故障冲击信号[7]。虽然MCKD的优化指标相关峭度(CK)可以考虑轴承故障冲击发生的周期性，但其主要缺陷在于存在其重要参数需人工预先设定，且参数的选择将会影响最终解卷积处理结果。

滚动轴承早期故障振动信号比较微弱，受传递路径影响之外还受到强背景噪声以及偶然性冲击影响，因此早期故障信息特征难以提取。共振解调方法在故障冲击引起的轴承系统共振频率附近进行带通滤波，能消除大部分噪声和干扰影响，最后通过滤波信号的包络谱进行轴承故障诊断[8]。Antoni[9]提出快速谱峭度方法(Kurtogram)，以1/3-二进分布的有限脉冲响应滤波器对整个信号的频带进行划分，并以滤波信号时域峭度最大的频带作为最优带通滤波频带。Kurtogram虽然为共振解调中带通滤波器中心频率及带宽的选择提供了一种方法，但其以信号时域峭度值作为度量指标存在与前述MED同样的缺陷，即该指标不能考虑轴承故障冲击信号的周期性特点，因而容易受外界偶然冲击的影响。Zhang等[10-11]结合1/3-二进滤波器组和小波包分解，提出了两种改进的Kurtogram方法对滚动轴承进行故障诊断。可调品质因子小波变换(tunable Q-factor wavelet transform，TQWT)是一种改进的小波变换，通过调节品质因子Q值得到不同的小波基函数，从而实现与待提取故障特征之间的最佳匹配，因而将其用于共振解调滤波有望获得更好的滤波效果[12]。然而其品质因子Q的选择严重影响最终滤波频带的选择，合适的频带评价指标是保证最终滤波效果的关键。

近年来越来越多的学者开始研究将多种信号处理方法复合使用，以期提高滚动轴承故障诊断效果。Su等[13]采用多点最优最小熵反褶积消除传递路径影响，进一步对信号进行改进经验小波变换，以时域峭度最大为指标选取IMF分量完成故障诊断。Shang等[14]利用经验模态分解(empirical mode decomposition,EMD)对原始信号进行分解，以互相关系数为优化指标选择最佳分量，进一步用Kurtogram进行共振滤波。Li等首先采用峭度为优化指标，首先对原始信号进行本征特征尺度分解(ICD)预处理，进一步根据特征频域比选择TQWT最佳分量进行分析。Ma等[15]首先对原始故障信号进行频率切片小波变换(FSWT)预处理，然后依据峭度最大指标采用改进的TQWT对预处理信号进行分解，对最佳分量进行故障分析。上述文献均以多种信号处理方法复合使用的方式进行滚动轴承故障诊断，虽然处理效果相比采用单一方法得到了提高，但仍存在一些问题。首先，涉及信号处理参数优化或分量选择时，大多优化指标易受偶然性干扰冲击影响，未考虑滚动轴承故障冲击特征周期性发生的特点；其次，复合诊断方法中预处理与后处理等步骤中的信号处理方法往往使用不同的优化指标，无法保证各步骤优化方向的一致性，从而影响诊断效果。

基于上述分析，本文提出一种预处理与后处理优化指标一致的滚动轴承故障复合诊断方法，其中优化指标采用能够考虑轴承故障冲击周期发生特点的相关峭度CK，以有效消除偶然性干扰冲击影响。预处理阶段采用MCKD削弱信号传递路径影响，后处理阶段通过TQWT降低噪声干扰，最后通过TQWT最佳分量的包络谱分析实现滚动轴承故障诊断。该方法的主要创新点在于前后两阶段的信号处理步骤一致以CK为优化指标，保证了优化方向的一致性，有望提高故障诊断效果。

1 方法介绍

1.1 最大相关峭度解卷积(MCKD)

MCKD由McDonald等在MED的基础上提出的一种以相关峭度(CK)为评价指标的新一代解卷积技术[16-17]。MCKD算法的本质就是寻找一个滤波器使得滤波后信号的CK最大。带有局部故障的滚动轴承运行时会产生周期性冲击信号y，但是由于信号受传递路径以及环境因素的影响，传感器采集到的信号为

x=h*y+e

(1)

式中：h为传输衰减响应；e为环境噪声;*号为卷积运算。

从实际采集的信号x中恢复出周期性冲击信号y，消除路径影响进而实现降噪、突出周期性故障特征，这一过程被称为解卷积。即：

(2)

经过M次移动后的相关峭度可以表示为

(3)

式中:TS表示迭代周期对应的采样点数;N表示输入信号的样本数;L表示FIR滤波器的长度。

MCKD故障特征增强的迭代过程如下：

步骤1输入由加速度传感器测得的振动信号x，以及确定故障周期T。

步骤3设置初始滤波器系数f=[0 0 … 1 -1 … 0 0]T；

步骤4计算滤波后的输出信号y;

步骤5根据y计算αm和β；

步骤6计算新的滤波器系数f；

步骤7根据下式计算迭代误差

(4)

如果计算出的err比给出的迭代误差小则计算终止；否则返回步骤3继续计算[18-19]。

1.2 可调品质因子小波变换(TQWT)

TQWT由Selesnick[20]于2011年提出，属于一种新型离散小波变换。与传统的恒定品质因子小波变换相比，TQWT的显著特点是可以通过自由调整品质因子Q值，不同的Q值对应不同的小波基函数，从而实现与待提取故障特征之间的最佳匹配。品质因子Q定义为中心频率与带宽的比值，如式(9)所示。

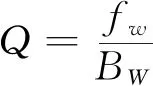
(5)

式中:fw表示振动信号的中心频率;BW为带宽[21]。

TQWT利用带通滤波器组以迭代方式实现信号的分解重构。滤波器组第J层的中心频率和带宽可由文献[22]得到

(6)

(7)

式中:J表示分解层数;α、β分别为高通、低通缩放参数;r为冗余;Fs为采样频率。

(8)

TQWT理论分解最大层数J的计算公式为

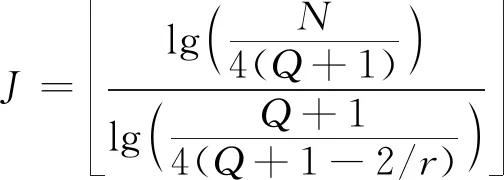
J=lgN4(Q+1) lgQ+14(Q+1-2/r)

(9)

由图1(a)可知，可调品质因子小波变换的时域波形是对称的，具有近似平移不变性，且分解层数J随着品质因子的增大而增大，当品质因子Q=3，前12层分解的频率响应如图1(b)所示。频率响应表示一组非恒定带宽滤波器，随着分解层数的增大，图1(a)中小波振动持续时间变得更长，图1(b)可见中心频率在逐渐降低。从高频开始的前10层带通滤波器已覆盖了0.05倍～0.5倍采样频率范围，根据常见的轴承采样频率与轴承系统共振频率关系可知，在Q=[1,3]范围内只需分析从高频开始的前10层子带信号即可，如此有利于减少计算量。

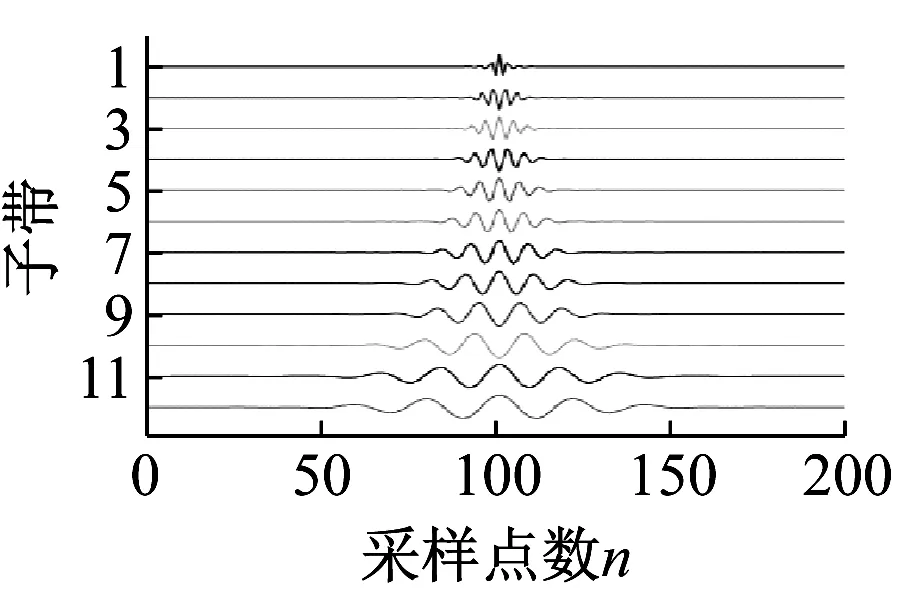
(a) 时域波形

1.3 提出的轴承故障诊断算法

本文提出一种优化指标一致的滚动轴承故障复合诊断方法，具体流程如图2所示，实现过程如下：

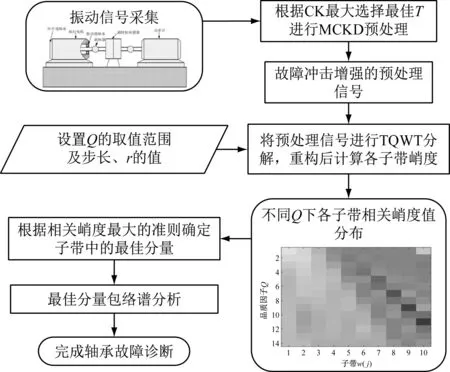
图2 本文所提方法流程图Fig.2 Flow chart of the proposed method

步骤1首先针对MCKD重要参数周期T的设定问题，根据轴承内、外圈以及滚动体故障对应的周期取并集，设定适当的周期区间T。在T的取值区间内以步长1依次对原始信号进行MCKD解卷积预处理，计算不同T值下解卷信号的CK值。以CK最大原则选择最佳T值用于解卷原始信号，消除传递路径影响并初步突出故障冲击；

步骤2设置TQWT中参数品质因子Q的取值范围、冗余因子r，将MCKD预处理后的信号在不同Q值下进行TQWT分解，得到相应的小波系数与一层尺度系数；

步骤3由于轴承故障冲击激发的共振频率通常位于中高频率，且参考图1所示，故不同Q值下的TQWT分解结果中只单支重构从高频开始的前10层子带信号，以减小计算工作量、提高算法效率；

步骤4计算各重构分量CK值，得到不同Q下的相关峭度分布图，根据相关峭度最大值选取最佳分量；求最佳分量的包络谱并与轴承的理论故障频率进行比较，完成故障诊断。

2 内圈仿真信号分析

在轴承实际运行时，信号中除了含有轴承自身的故障冲击和常规振动以外，还可能受到外界其它偶然性冲击干扰。偶然性冲击在振动信号中往往表现为幅值突然增大，冲击幅值通常能够达到轴承故障冲击的几倍，且不具有周期性。因此，偶然性冲击的峭度值会远大于轴承故障循环冲击的峭度值，从而影响最终的解调分析结果。本小节以仿真信号为例对该情况进行分析验证。

纯内圈故障仿真信号如图3(a)所示，其中内圈故障特征频率为90 Hz，信号采样频率为20 480 Hz，轴承结构共振频率为3 500 Hz。为了使仿真信号更接近轴承实际运转时所产的振动信号，在内圈故障冲击信号中加入幅值为0.4的高斯随机噪声如图3(b)所示。为了表明峭度易受高幅值偶然性干扰冲击的影响，在信号中1 000～1 060点范围内人为添加一段幅值为10、频率为1 500 Hz的正弦信号，结果如图3(c)所示。可见内圈故障冲击在高斯噪声和正弦冲击干扰下已无法从时域明显辨识，图3(d)包络谱中未能发现有效的故障特征频率成分。

(a) 原始内圈故障仿真信号

为了使本文方法的试验结果更具有说服力，首先采用Kurtogram对图3(c)所示的内圈故障仿真信号进行分析，根据滤波器带宽与最大故障特特征频率之间的要求(带宽>3×最大故障特征频率)设置谱峭度的分解层数为3，得到图4(a)的谱峭度图。所选择的最佳滤波频带参数为：中心频率1 900 Hz，带宽800 Hz，恰好涵盖了人为添加的正弦干扰冲击频率1 500 Hz。对应频带滤波后的包络信号如图4(b)，仅存在明显的偶然性冲击成分。包络谱图4(c)中无任何故障频率成分，无法判断滚动轴承存在故障。究其原因，在于峭度指标未考虑故障冲击的周期性特点，在高幅值冲击的干扰下，导致滤波频带选择错误，最终Kurtogram方法诊断失败。

(a) 谱峭度图

采用本文方法所得分析结果如图5所示。根据滚动轴承故障特征频率计算公式，设内、外圈以及滚动体故障特征频率分别为90 Hz、80 Hz、75 Hz，对应的周期T分别为227、256、273，因此可设置参数T的取值范围为[220,280]。利用不同的T值对图3(c)所示的内圈故障仿真信号进行MCKD解卷积预处理，根据CK最大准则所得最佳周期T为226，与实际内圈周期T=227接近。预处理结果如图5(a)，图中可见偶然性冲击和传递路径影响得到一定的抑制，故障冲击成分得到初步增强，但不足以判断轴承故障发生情况。

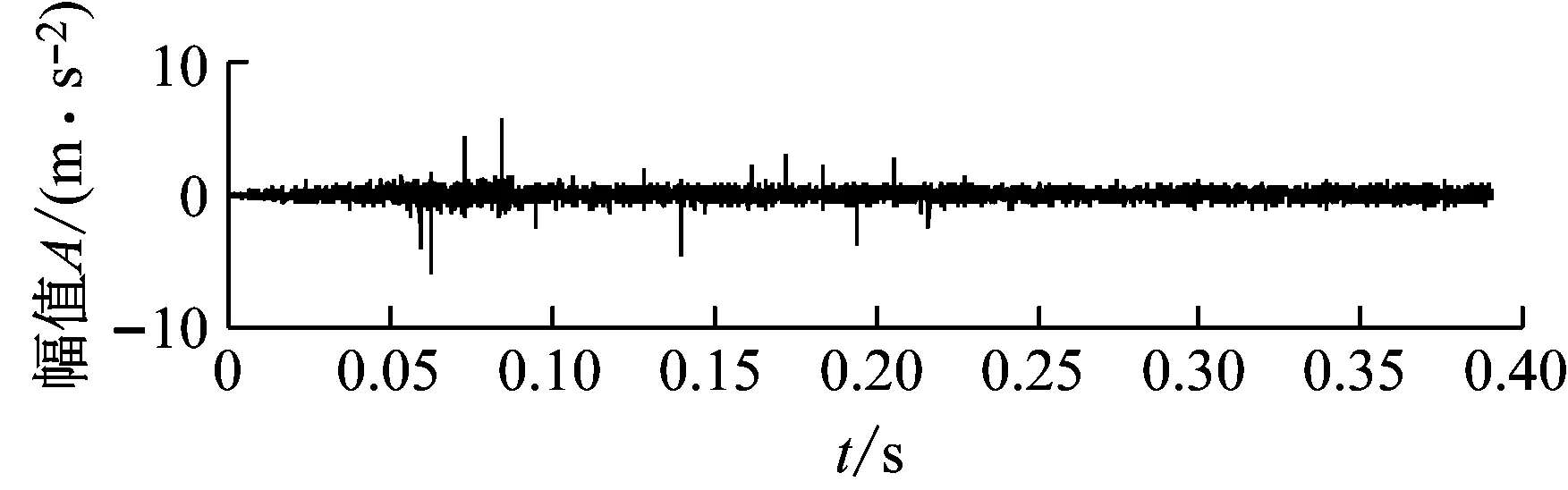
(a) MCKD预处理后信号

进一步对预处理后信号进行TQWT分解，设置品质因子Q的变化范围为[1.0，3.0]，步长为0.1，冗余因子r为4.0。取分解后每个Q值对应的前10层小波系数并进行单支重构，求各个重构分量的CK值，得到如图5(d)所示的TQWT各子带分量相关峭度图。根据图5(d)中CK值最大原则，得到最佳TQWT分量。最佳分量对应的Q为1，层数为该Q下的第1层，其对应的滤波器为第一层的高通滤波器。其对应的滤波器频带开始于2 000 Hz，覆盖该仿真信号的共振频率3 500 Hz，且有效避开了加入的正弦干扰冲击频率1 500 Hz，证明了该方法对偶然性冲击干扰具有较好的鲁棒性。最佳分量时域波形如图5(b)，可以看到冲击成分得到了明显的增强。其包络谱如图5(c)所示，包络谱中可以看到89.6 Hz的频率成分与内圈故障特征频率90 Hz非常接近，幅值明显且存在边频带，且存在181.8 Hz、271.4 Hz等明显倍频成分，可以判断此时轴承发生了内圈故障。仿真信号分析结果表明本文方法在噪声和偶然性干扰冲击下仍能有效提取滚动轴承故障特征。

本文方法的主要创新点在于预处理和后处理均一致采用考虑故障冲击特征周期发生特点的CK值最大作为优化准则，这与当前许多文章前后处理优化指标不一致存在明显区别[23]。为了体现本文所提方法的优势所在，将本文TQWT后处理阶段优化指标替换为常规时域峭度，其余步骤及参数均不变。图6(a)为TQWT各子带分量的峭度值分布图，最佳分量对应的Q为2。对应滤波器中心频率为1 759 Hz，恰好涵盖了设置的干扰冲击频率1 500 Hz。最佳分量时域波形如图6(b)，包络谱图6(c)中没有明显的故障特征频率成分，无法判断滚动轴承是否存在故障。故此方法诊断失败,印证了本文所提方法的必要性。

(a) 各分量的峭度值

3 试验数据分析

3.1 含偶然性冲击的故障信号分析

试验数据来源于美国Case Western Reserve大学轴承数据中心，故障模拟试验台如图7所示。该试验台由一个1.491 kW的电机、一个扭转传感器、编码器、一个功率计和控制电子单元组成。本文选取驱动端轴承滚动体故障数据进行分析，采用电火花加工技术在轴承滚动体上加工不同尺寸的故障。为体现本文的方法在轴承早期微小故障的作用，选取最小直径0.007 mm的数据进行分析。该试验台使用的轴承是深沟球轴承，编号为SKF-6205，内圈直径25 mm，外圈直径52 mm，滚动体直径7.94 mm，轴承节径39.04 mm，厚度15 mm。通过公式计算出轴承滚动体故障特征频率fb为68 Hz，轴承的转频fr为15 Hz。

图7 试验装置图Fig.7 Experimental setup

图8(a)为在数据样本中随机选取的6 000个采样点，可以看到冲击成分几乎都被噪声覆盖。为了验证笔者所提方法的有效性及合理性，进一步在信号中1 000～1 060点范围内人为添加一段幅值为10的高幅值偶然性冲击如图8(b)所示，可见振动信号被严重影响，且在包络谱图8(c)中无法判断轴承是否发生故障。

(a) 原始滚动体故障信号

处于比较的目的，首先采用Kurtogram对图8(b)的信号进行分析，同仿真信号分析一致，设置分解层数为3，得到的谱峭度图如图9(a)所示，可见谱峭度受偶然性冲击影响严重。滤波后信号包络如图9(b)，可以看到明显的偶然性干扰冲击，无明显周期性故障冲击特征。图9(c)的包络谱中未出现明显特征频率成分，无法判断滚动轴承存在故障,故Kurtogram方法诊断失败。

(a) 谱峭度图

采用本文方法所得分析结果如图10所示。设置T的取值范围为[70,200],得到最佳故障周期T=175，与实际滚动体周期相符。预处理信号如图10(a)所示，时域波形中可见冲击特征得到一定增强。进一步进行TQWT分解重构，对应最佳滤波信号时域波形及其包络谱分别如图10(b)和(c)，可见68 Hz、134 Hz等倍频成分明显，可以判断此时轴承发生滚动体故障。因此凯斯西储滚动体故障数据分析结果验证了本文方法在强干扰下诊断故障的可行性。

(a) MCKD预处理后信号

为了进一步体现本文提出的前后处理采用一致的优化指标这一观点的意义，将本文方法的TQWT后处理阶段优化指标替换为常规时域峭度，其余参数均不变。得到最佳分量时域波形如图11(a)，其包络谱如图11(b)所示，包络谱中虽然显示出90 Hz及其倍频成分，但与实际故障特征频率不符。故此方法诊断失败，印证了预处理与后处理一致采用考虑故障冲击周期发生特点的CK指标的必要性。

(a) 最佳分量时域图

3.2 轴承疲劳试验早期故障数据分析

轴承早期故障表示轴承故障处于发生的萌芽阶段，冲击特征微弱，若能准确地诊断出早期故障，则能为设备的维修和生产计划的安排争取足够多的时间。本节对美国辛辛那提大学智能维护中心提供的轴承疲劳寿命试验数据进行分析，该疲劳试验台如图12所示。整个轴承疲劳寿命试验共历时7天，试验结束后对试验台进行拆解发现轴承1出现较为严重的外圈故障，计算得轴承外圈故障特征频率为236.4 Hz。

(a) 试验台结构简图

试验过程共采集了984组数据。采样频率为20 000 Hz，数据长度为20 480点，全寿命周期的均方根值(RMS)演化情况如图13(a)所示。因此第534组可以认为轴承正处于故障的萌芽状态[8]。其波形图及包络谱分别如图13(b)和(c)所示。包络谱中虽然有一处明显的230.5 Hz频率成分，但在[500,1 000]Hz这一频率范围内也出现了其它一些与故障特征频率无关的谱峰，同时未出现明显的故障倍频成分，因此无法确切判断存在外圈故障。

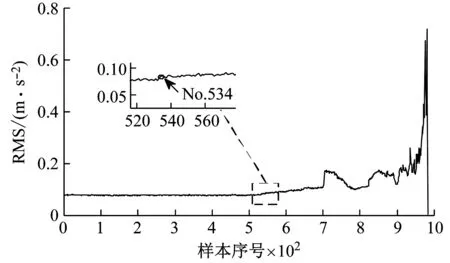
(a) 疲劳试验全寿命周期RMS演化

采用常规方法Kurtogram对图13(b)信号进行对比分析，谱峭度图14(a)中最优中心频率为7 500 Hz，带宽为1 666 Hz。滤波后信号包络如图14(b)所示，包络谱图14(c)中只存在与外圈故障特征频率BPFO相近的230.4 Hz频率成分，无明显倍频成分，因此不能确切判断滚动轴承是否存在故障。

(a) 谱峭度图

采用本文方法的轴承早期故障分析结果如图15所示。设置T的取值范围为[65,110],得到最佳故障周期T=86，与实际内圈故障周期85接近。预处理后信号如图15(a)的时域波形中冲击特征有所增强。进一步进行TQWT分解重构，图15(d)相关峭度分布图对应最佳滤波信号时域波形及其包络谱分别如图15(b)和(c)，可见232 Hz及其倍频成分明显，可以判断轴承发生外圈故障。该案例分析表明本文方法在轴承早期微弱故障特征提取中具有一定的可行性和优越性。

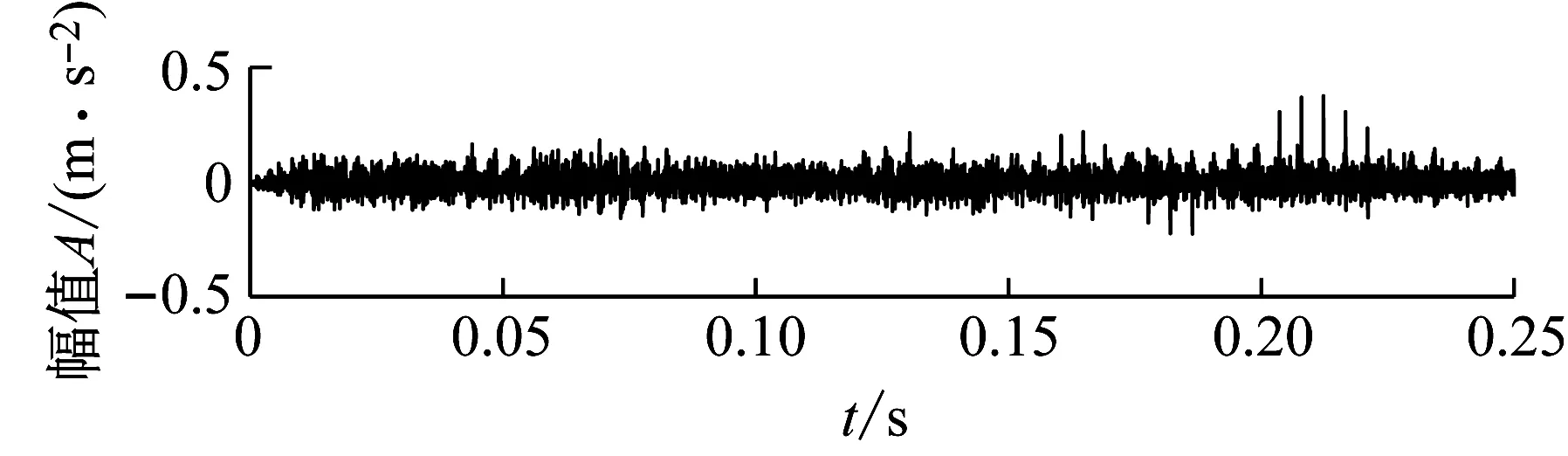
(a) MCKD预处理后信号

4 结 论

针对大多滚动轴承故障复合诊断方法中所采用的优化指标缺乏考虑滚动轴承故障冲击周期发生特点，同时各信号处理步骤采用的诊断优化指标不一致，导致轴承故障诊断效果不佳的问题，提出了预处理和后处理均以相关峭度为优化指标的滚动轴承复合诊断方法，以减小偶然性干扰冲击、传输路径等因素对处理结果的影响，保证了特征提取效果的一致优越性。仿真信号、实验室信号、以及疲劳试验数据表明：

(1) 由于一致采用CK为优化指标，基于MCKD预处理和TQWT后处理的轴承故障复合诊断方法能有效排除外界偶然性干扰冲击影响并降低信号传递路径和噪声影响，从而保证轴承故障诊断的有效性；

(2) 合理设置MCKD中故障周期T的取值范围并以CK最大原则对T值进行寻优，有效解决了转速波动等因素影响导致的计算故障周期与实际故障周期之间的差异问题，从而有效保障MCKD 算法效果；

(3) 与Kurtogram以及文中所举例的前后优化指标不一致的复合诊断方法的比较结果表明本文方法在轴承故障诊断方面更具优势。