基于AR-GP模型的结构损伤识别方法

唐启智，辛景舟，周建庭，付 雷，周滨枫

(1.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074；2.贵州桥梁建设集团有限责任公司，贵阳 550000；3.重庆大学 土木工程学院，重庆 400074)

随着服役年限的增加，工程结构物在运营过程中由于荷载效应、材料劣化、环境侵蚀等因素的作用，其使用性能不断恶化。识别结构的早期损伤，掌握其健康状况，有着重要的科学研究意义与工程实用价值[1]。

结构损伤将导致结构固有特性的改变，从而引起结构响应的变化。结构损伤识别从结构响应出发，以期获得结构的损伤状态，其核心环节即是损伤敏感性特征(damage sensitive feature,DSF)的提取[2]，常用的提取方法[3]包括频域方法和时域方法。频域方法通过实验模态分析，以频率变化率[4]、模态曲率[5]、模态应变能[6]等作为DSF进行损伤识别。时域方法在时间域上对测试数据进行分析，结合时间序列分析[7]、经验模态分解[8]等方法来提取DSF。与频域方法相比，时域方法由于不需要进行繁琐的频谱分析，越来越受到广泛关注[9～10]。

自回归(autoregressive,AR)模型作为时域方法中的重要组成部分，常被用于回归拟合结构加速度响应数据，并从中提取DSF。Lynch[11]通过对AR模型方程进行Z变换，证明了AR模型系数与结构固有特性相关。Nair等[12]以AR模型前三阶系数构造DSF，使用t检验进行了损伤识别及定位。Datteo等[13]通过全局敏感性分析和不确定分析，得出了AR模型系数对结构刚度与质量变化较为敏感，对阻尼与荷载的变化不敏感。杜永峰等以结构损伤前后AR模型残差方差之比作为损伤指标，通过数值算例定性的实现了结构损伤识别及定位。朱军华等[14]以AR模型残差的偏度和峰度作为DSF，取得了一定的识别效果。可见，将AR模型用于DSF的提取展现出了极大的应用潜力与科研价值。

获取DSF后，结构损伤识别就归结为模式识别的问题。机器学习作为模式识别的主要方法，包括神经网络[15]、支持向量机[16]、高斯过程等。高斯过程(Gaussian process,GP)是一种常用的监督学习方法，旨在解决回归问题和概率分类问题，包括高斯过程分类(Gaussian process classification,GPC)和高斯过程回归(Gaussian process regression,GPR)。Sawant等[17]基于GP提出了一种分层算法，实现了人脸年龄估计。舒坚等[18]利用GPR进行了链路质量预测，取得了比动态贝叶斯网络更精确的结果。朱彬等[19]提出了一种基于GPR的响应面拟合方法，并实现了边坡可靠度分析。程虎等[20]利用GPR实现了成像系统参数的在线优化。由此可以看出，GP在生物识别、状态预测、参数优化等方面有较多应用，但在损伤识别领域却很少见。损伤识别分三个阶段：一是识别损伤；二是定位损伤；三是识别损伤程度。实际过程中由于建模误差、测量噪声的影响，观测值近似随机过程，结合GP具有概率意义的输出特性，将GPC用于损伤定位、GPR用于识别损伤程度，能使输出结果更具信服力，因此将GP运用于损伤识别凸显了巨大的工程实用价值。

考虑到损伤识别的复杂性与既有方法的不足，本文提出了一种基于AR-GP模型的损伤识别方法。首先，利用AR模型回归拟合结构加速度响应数据；然后，根据AR模型的残差、系数分别构造DSF；最后，借助GPC与GPR分别识别结构损伤位置与损伤程度。通过某钢筋混凝土模型拱的数值算例，验证了所提出的损伤识别方法。

1 自回归模型

1.1 建模方法

如果一个随机过程中的观测量Yt可以表示为

Yt=c+φ1Yt-1+φ2Yt-2+…+φpYt-p+εt

(1)

AR模型建模步骤如下：(1)数据平稳性检验；(2)数据标准化处理；(3)模型识别；(4)参数估计。

数据平稳性检验即为单位根检验，本文采用ADF检验法[21]。ADF检验包括三个检验模型

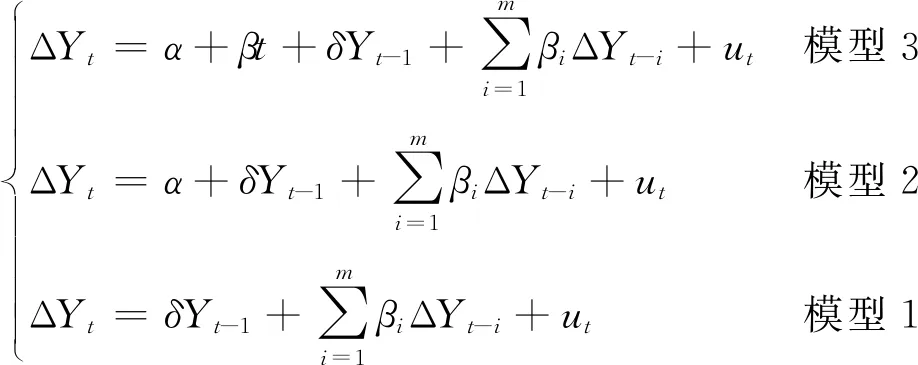
(2)

三个检验模型中α、β、δ为最小二乘回归系数。实际检验过程中从模型3～模型1依次检验，若有任何一个模型拒绝零假设，则认为序列不存在单位根，即序列平稳。各个模型原假设如下

(3)

数据标准化处理的目的是为了消除噪声及荷载对测试数据的影响，计算公式如下

(4)

式中，u、σ分别为响应数据的均值和标准差。

模型识别即确定AR模型滞后阶数p，根据AR(p)模型偏自相关函数p阶截尾的特点，可通过计算偏自相关函数来确定p。但实际过程中理论偏自相关函数难以获取，故本文采用样本偏自相关函数[22]与AIC准则[23]联合来确定p。

(5)

(6)

(7)

确定好AR模型的滞后阶数p之后，选取最小二乘法进行模型参数估计，基本思想为寻找使得模型残差平方和最小的一组参数值，即：

(8)

1.2 基于残差的损伤敏感性特征

建立好AR模型之后，即可提取DSF进行损伤识别工作。综合国内外研究成果，常用的DSF大致分两类：基于残差的DSF和基于自回归系数的DSF。本文分别建立了基于残差和自回归系数的DSF，并对其预测结果进行了对比分析。

针对损伤识别过程中，定位损伤位置困难、多损伤状态不易识别的问题，引入了表征结构损伤位置信息与损伤状态信息的参数L1、L2

(9)

(10)

式中：i代表传感器编号，i=1,2,…,d；DSFi表示第i个传感器的DSF。

结构发生损伤后，对应AR模型残差标准差(residual standard deviation,RSD)会发生变化，于是构造基于残差标准差的DSF

DSFi=σεi

式中,σεi表示第i个传感器处残差标准差，i=1,2,…,d。

在损伤定位时，引入参数L1、L2，定义基于残差标准差的GPC输入向量RSD1

RSD1=(σε1,σε2,…,σεd,L1,L2)

在识别损伤程度时，定义基于残差标准差的GPR输入向量RSD2

RSD2=(σε1,σε2,…,σεd)

1.3 基于自回归系数的损伤敏感性特征

根据文献[11]，AR模型系数与结构固有特性存在一定的联系，因此基于自回归系数(autoregressive coefficient,ARC)的DSF表述如下

其中，φj,j=1,2,…,p为AR(p)模型系数；φi为第i个传感器处的DSF，i=1,2,…,d。

同样在损伤定位时，引入参数L1、L2，定义基于自回归系数的GPC输入向量ARC1

ARC1=(φ1,φ2,…,φd,L1,L2)

在识别损伤程度时，定义基于自回归系数的GPR输入向量ARC2

ARC2=(φ1,φ2,…,φd)

2 高斯过程

2.1 高斯过程回归

GP是符合多维联合正态分布随机过程的总称。对于给定的训练数据集

D={(X,y)|X={x1,x2,…,xN}T∈RN×d,y∈RN}

其中X、y分别为输入和输出变量，且N、d分别为输入变量个数及输入变量维数，y用于描述输入变量的随机过程，且服从GP，其性质由均值函数E(y)、协方差函数K决定：

y～N(E(y),K)

其中K也叫做格拉姆矩阵，其元素为：

Kij=K(xi,xj),(i,j=1,2,…N)

高斯过程回归(GPR)是基于贝叶斯理论和统计学习理论发展起来的一种新的机器学习方法，适用于处理高维数、小样本、非线性等复杂回归问题，近几年来在国内外发展迅速[25]，其本质是基于贝叶斯推断，在给定输入的情况下，给出输出的条件分布，其基本步骤包括训练与预测。

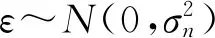
(11)

GPR的关键是协方差函数K，即核函数的选取，包括线性核、多项式核等，使用频率最高的是平方指数核，即：

(12)

(13)

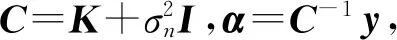
其中k是K(xi,x*)(i=1,2,…,N)的N×1维向量，r=K(x*,x*)。

根据贝叶斯推断，可得预测值y*的后验分布为

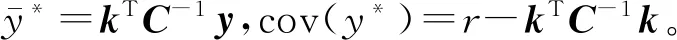
2.2 高斯过程分类

当GPR中的连续型输出变量变为离散的类别向量时，GPR就演化为高斯过程分类(Gaussian process classification,GPC)。

GPC的基本思想是首先赋予隐函数f(x)的高斯过程先验分布；然后引入反应函数获取先验分布π(x)=p(y=1|x)=σ(f(x))；最后输出类别概率最高的分类结果。

对于给定的输入x*，f*=f(x*)的分布以及类别预测概率分别按式(14)、(15)计算：

(14)

(15)

由于输入变量非连续，似然函数p(y|f)服从非高斯分布，式(14)、(15)无法获取解析解，常采用拉普拉斯近似方法求解[26]。

2.3 损伤识别流程

基于AR-GP模型的损伤识别方法的大致流程为：

(1) 获取结构在各个测点的加速度响应数据；

(2) 根据1.1节所提建模方法，建立AR模型；

(3) 构造DSF：计算RSD1、RSD2，ARC1、ARC2；

(4) 损伤识别：首先，以RSD1、ARC1为输入向量，损伤位置为分类标签，利用GPC实现损伤定位。然后，以RSD2、ARC2为输入向量，损伤程度为输出，利用GPR识别损伤程度。算法流程如图1所示。

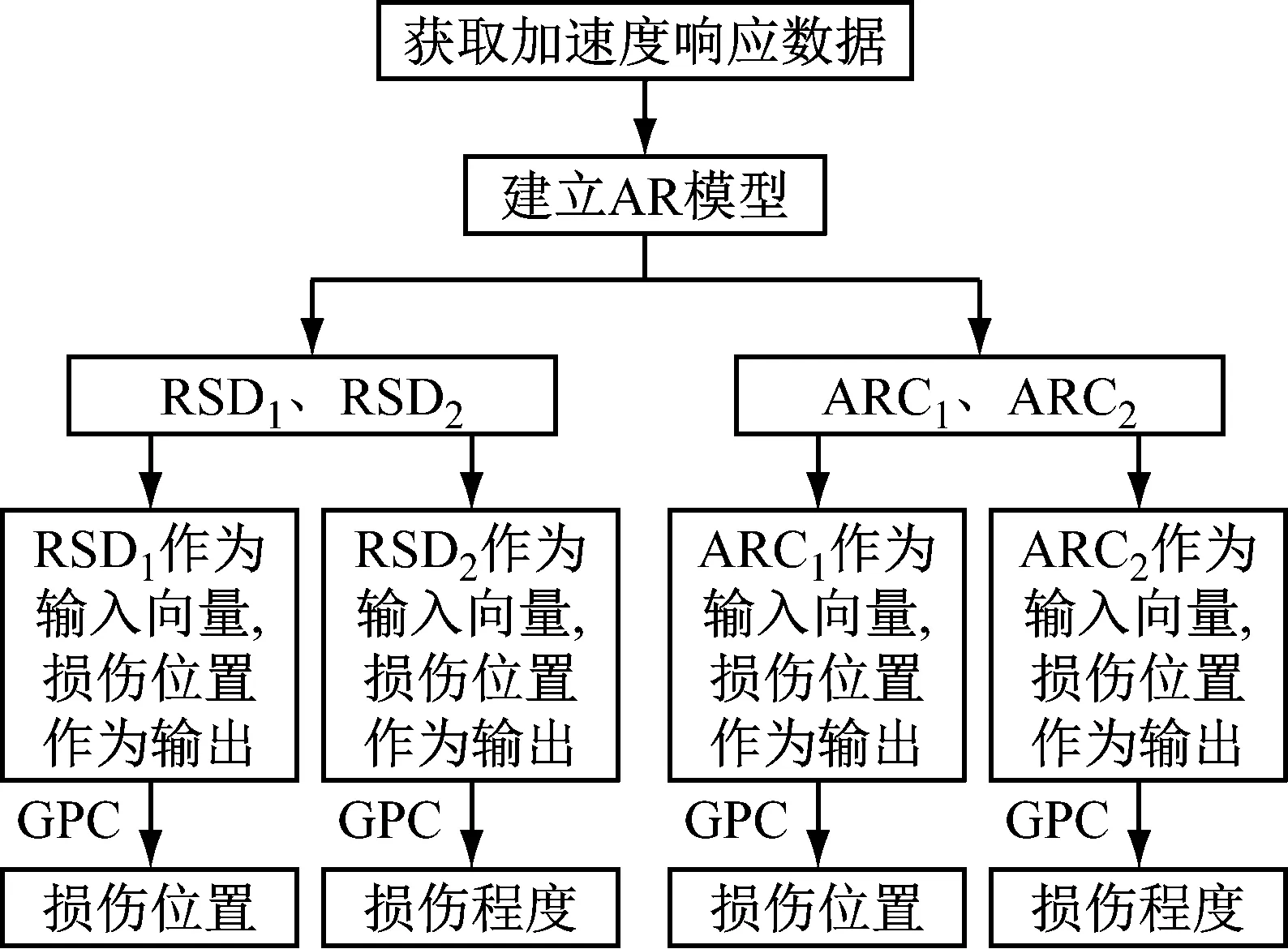
图1 AR-GP算法流程图Fig.1 Flow chart of AR-GP algorithm

3 实例验证

3.1 钢筋混凝土拱模型

本文所采用的数值模拟对象为某钢筋混凝土模型试验拱，拱肋沿跨径方向划分成9个节段，共布置了7个加速度测点，其具体尺寸参数如图2所示。

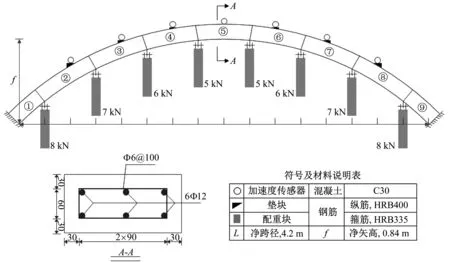
图2 模型拱基本构造Fig.2 Basic structure of model arch

利用ANSYS通用有限元软件建立结构有限元模型，采用分离式建模方法。混凝土采用SOLID65单元，加载块采用SOLID45单元，钢筋采用LINK8单元。有限元模型共划分为2 888个单元，如图3所示。

图3 ANSYS有限元模型Fig.3 Finite element model of ANSYS

边界条件以面约束的形式施加，约束两拱脚所有平动及转动位移；配重通过加载块的自重来施加，并根据其实际重量及加载块体积换算等效密度。随后，进行了瞬态分析。

瞬态分析采用完全法，结构阻尼采用瑞利阻尼，质量阻尼系数α与刚度阻尼系数β按下式计算

(16)

式中:ωi和ωj分别为结构第i和第j阶固有频率，可通过模态分析获取；ξi和ξj为相对应于第i和第j阶振型的阻尼比；一般取i=1，j=2，ξi=ξj=0.05。

在拱肋7L/16处施加白噪声激励，采样频率为1 000 Hz，采样时间为0.5 s。

3.2 损伤工况

结构损伤显著影响结构的刚度，刚度退化通过弹性模量的折减来实现。本文考虑了36种损伤工况，包括单损伤、多损伤，以及不同损伤程度的情况，其中有24种(A1～A24)训练工况以及12种(B1～B12)测试工况，损伤工况见表1。

表1 损伤工况Tab.1 Damage scenarios

为模拟实际的测试环境，对有限元提取的加速度响应数据施加了一定程度的白噪声干扰，按下式计算[27]

anoise=a+RMS(a)×Nlevel×Nunit

(17)

式中：anoise、a分别为含有噪声与未含噪声的加速度响应数据；RMS(a)为a的均方根；Nunit为高斯白噪声；Nlevel为所施加的噪声水平，本文选为5%和10%。

3.3 结果分析

根据加速度响应建立AR模型，然后计算各个工况、各个测点所对应的RSD1、RSD2、ARC1、ARC2，核函数采用平方指数函数与白噪声函数相加的形式，基于训练样本，利用sklearn机器学习库对GPC、GPR进行训练，然后将测试样本送入已经训练好的GPC、GPR进行损伤定位及识别损伤程度。

3.3.1 损伤定位结果

基于残差标准差和自回归系数的损伤定位结果见表2。

从表2的损伤定位结果可知，随着噪声水平的增加，识别精度逐渐降低，但总体而言，基于残差标准差的识别方法具有较好的识别精度以及抗噪性，且对于单损伤和多损伤状态有较好的区分能力；而基于自回归系数的识别方法则表现出较差的识别精度与抗噪性。

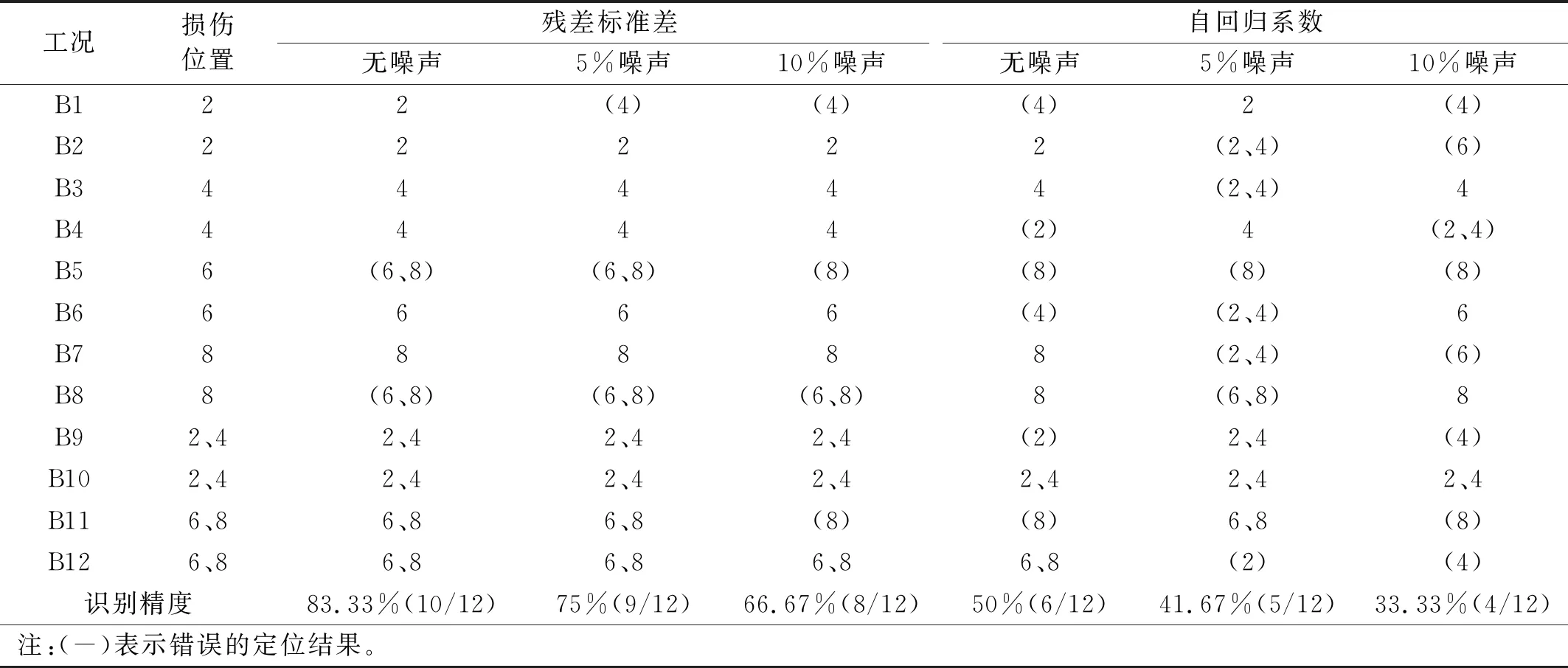
表2 损伤定位结果Tab.2 Results of damage localization

3.3.2 损伤程度识别结果

基于残差标准差和自回归系数的损伤程度识别结果分别见表3、表4。表中:u表示识别结果的均值；σ表示识别结果的标准差；RE表示识别结果的相对误差；DC表示识别结果的离散系数。

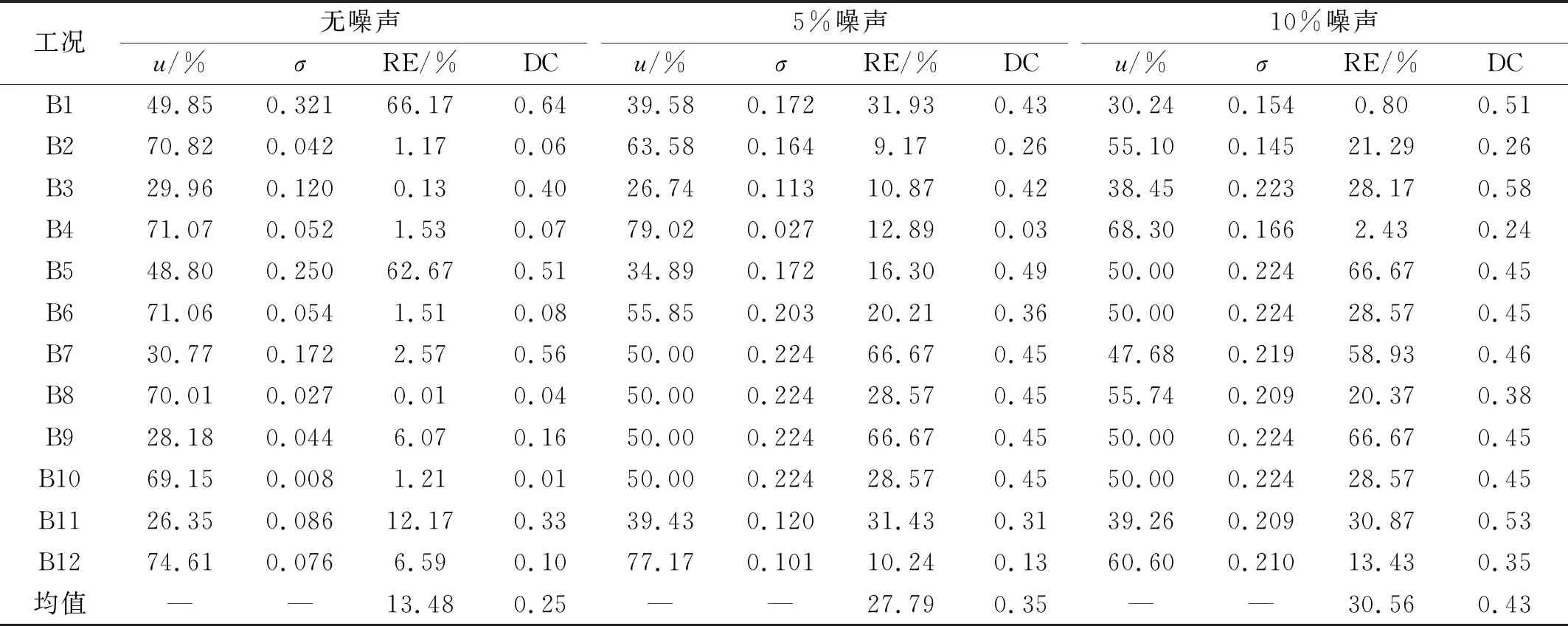
表4 基于自回归系数的损伤程度识别结果Tab.4 Results of damage severity identification based on autoregressive coefficient

从表3的损伤程度识别结果可以看出，随着噪声水平的增加，RE与DC的均值变化不大，且处于较低的水准，在10%噪声污染的情况下，识别结果的RE与DC值也仅仅为6.52%和0.19。DC越接近于0，表明识别结果波动性越小、越可靠，故可以认为基于残差标准差的方法有很高的识别精度及可靠度，且抗噪性能好。

表3 基于残差标准差的损伤程度识别结果Tab.3 Results of damage severity identification based on residual standard deviation

从表4可知，与基于残差标准差的识别结果相比，基于自回归系数的识别精度及可靠度则相对较低，抗噪性能差。

图4是所有识别结果的RE与DC散点图，从图中可以看出RE与DC呈现出较强的正相关性。在实际的监测过程中，由于无法知晓预测结果的真值，也就不能获取预测结果的RE。此时，可以根据DC判断预测结果的精确度以及波动程度，由此做出预测结果是否可接受的判断，从而提高了识别可信度。

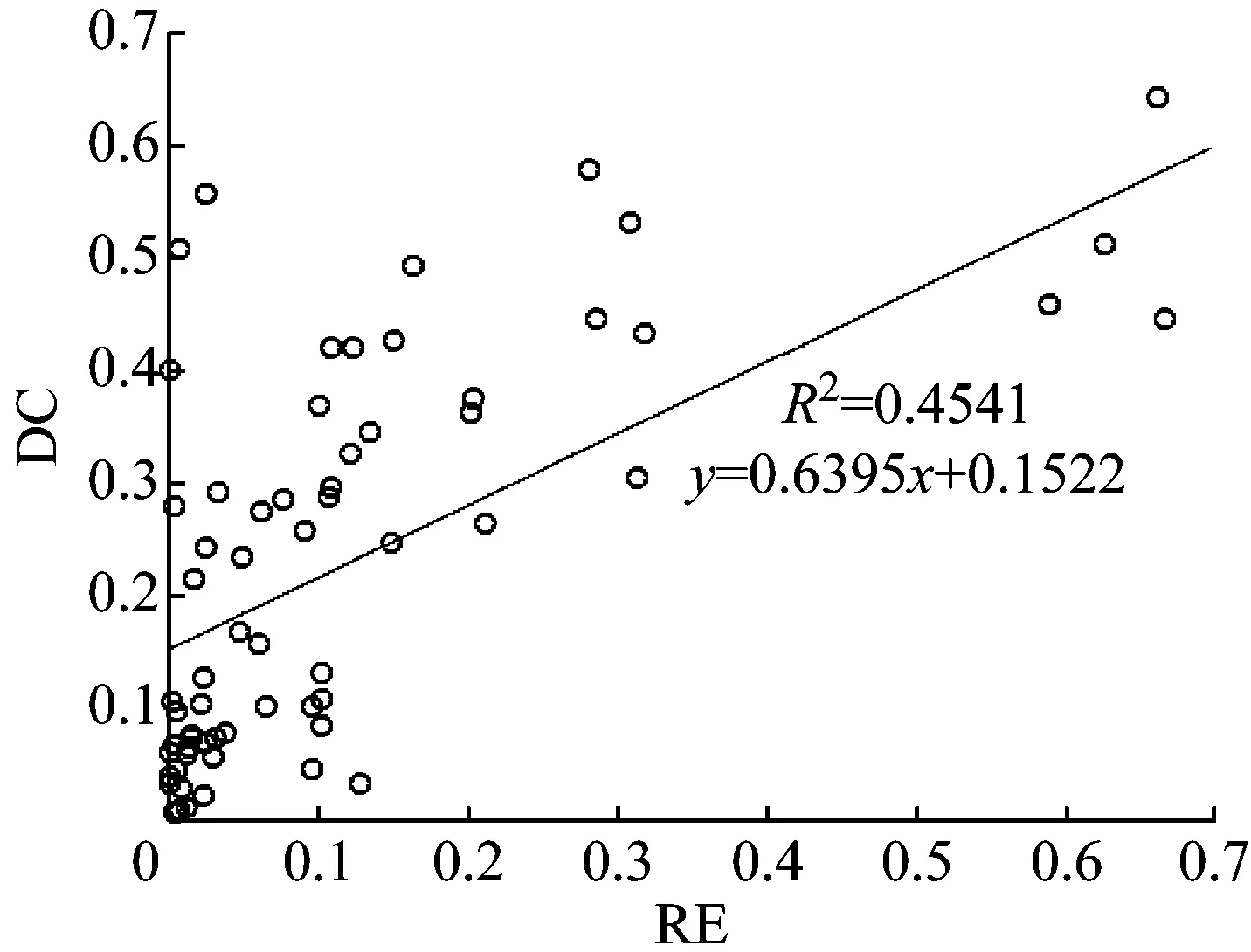
图4 RE与DC关系Fig.4 The relationship between RE and DC

另外，利用GPR输出结果概率分布的特点，在实际结构的监测过程中可以实现损伤预警，如图5所示，其基本思想为：如果预测结果有1-α的概率超过给定的损伤程度，则发出预警。图中:η为损伤程度;ηt为损伤阈值;ηα为根据特定问题所规定的下α分位点。

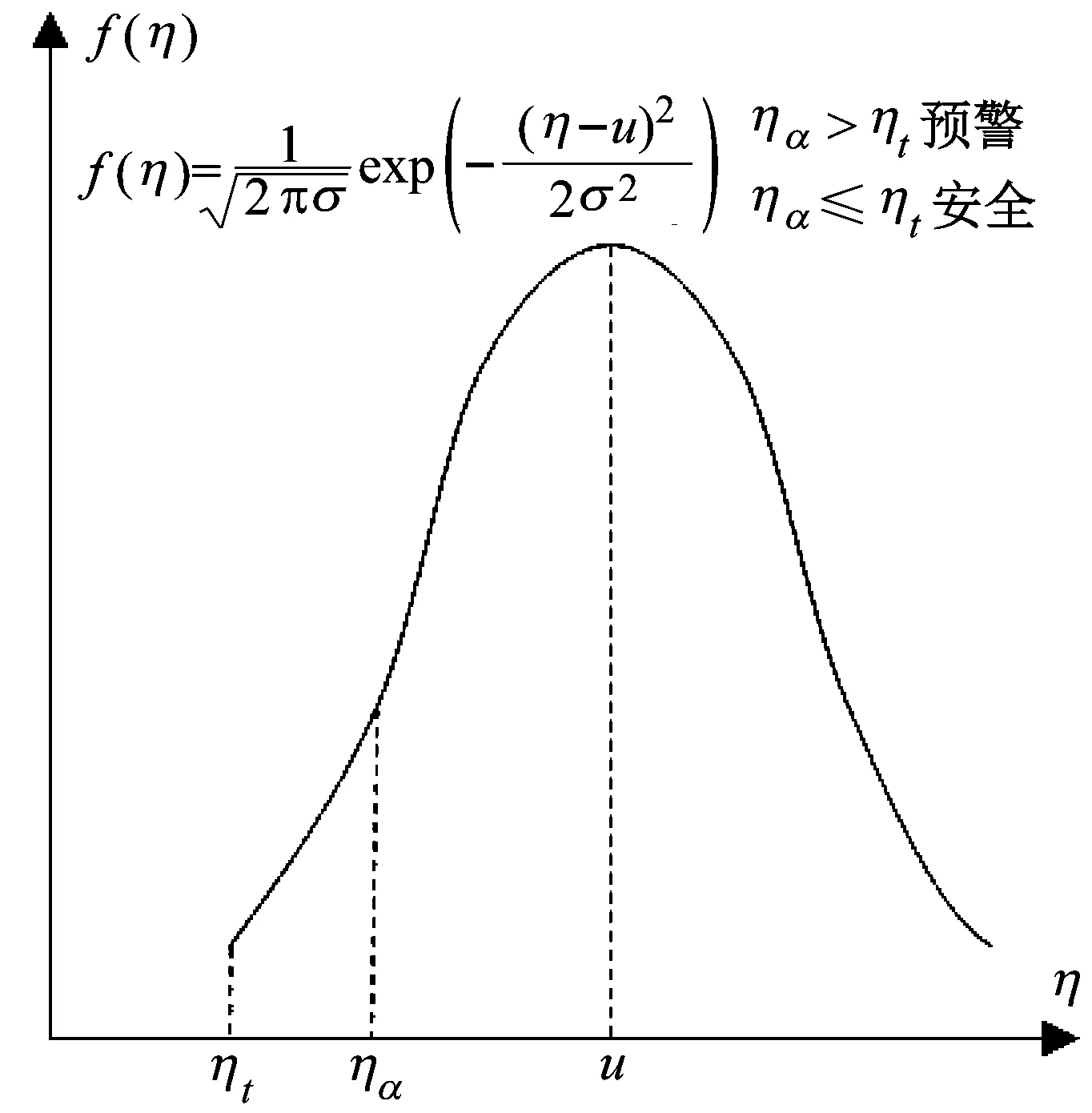
图5 损伤预警Fig.5 Damage alarming

4 结 论

本文提出了一种基于AR-GP模型的全新的结构损伤识别方法。该方法利用AR模型回归拟合结构加速度响应数据，并从中提取DSF，首次引入损伤位置信息与损伤状态信息参数L1、L2，基于GPC实现了结构多损伤定位，借助于GPR实现了损伤程度的概率结果输出。通过36种不同损伤工况的数值算例，验证了所提方法，并对基于残差标准差和自回归系数的识别结果进行了对比分析，得出了以下结论：

(1) 在损伤定位方面，所提识别方法能够较好的区分单损伤和多损伤状态，同时基于残差标准差的定位结果较基于自回归系数的结果有更好的识别精度与抗噪性能。在识别损伤程度方面，基于残差标准差的识别结果表现出了良好的识别精度、可靠度与抗噪能力，在10%噪声污染的情况下，识别结果的RE与DC值仅为6.52%和0.19，而基于自回归系数的识别结果的精度与抗噪能力则较差。

(2) 损伤程度识别结果的RE与DC展示出了较强的正相关性，在实际的监测过程中，可以由DC判断预测结果的精确度以及波动程度，能够提高识别可靠性。

(3) 利用GPR输出预测结果均值与方差的特性，建立相应的损伤阈值，从而可以实现损伤预警。值得一提的是，可通过可靠度理论，按一定的失效概率构造损伤阈值，这也是未来的研究方向。