冰区海上单桩风机振动响应与控制

朱本瑞，孙 超，黄 焱

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.路易斯安那州立大学 土木与环境工程学院,美国 70803)

随着世界各国对能源需求的增加，海上风能作为一种清洁可再生资源备受关注。根据全球风能理事会(Global Wind Energy Council,GWEC)2018年数据统计，世界范围内的风能发电量达到539 GW，并预测在未来5年内，以平均每年55 GW的装机总量速度持续增长[1]。我国海上风电事业起步较晚，但发展迅速，截至2019年6月底，海上风电累计装机容量已达403万千瓦，预计2020年，实现并网装机790万千瓦[2]。目前，海上风电不断向大型化发展，2019年，金风科技在江苏大丰海上风电中，安装了GW184-6.45 MW的海上风电机组，该机组搭载90 m叶片，是国内已投运机组中叶片直径最大的海上风力发电机组，刷新了亚太地区投运机组的最大叶轮直径记录[3]。

不同于陆上风电结构，海上风电服役环境恶劣，除承受风、浪、流等海洋环境载荷，在冰区海域还受到海冰的威胁。相对于风浪流载荷，海冰是一种极其特殊的载荷，受其温度、盐分、冰厚、冰速以及与之作用结构的刚度、作用面积和形状等参数的影响，具有复杂多变的失效模式和截然不同的作用机理。截至目前为止，学术界对冰与结构的相互作用机理仍未达成统一的认识[4]。文献[5]研究表明，海冰载荷是冰区海上石油平台设计的主要控制载荷，特别是其引起的冰激锁频振动现象(冰载频率与结构基频基本一致)，严重威胁结构的服役安全。位于我国辽东湾的JZ20-2平台现场监测表明，海冰与柔性直立桩结构相互作用易引发结构的强烈稳态锁频振动[6]；JZ9-3海洋平台的现场监测数据亦观察到了这一现象[7]；国外，美国阿拉斯加库克湾的钻井平台[8]，加拿大大型沉箱式采油平台[9]等都曾遭受到冰激锁频振动事件；而一系列的室内实验亦证实了冰激锁频振动的存在[10-11]。相对海上石油平台，海上风机结构，特别是被广泛采用的单桩风机基础，具有更柔的刚度，更易发生锁频振动现象[12]，从而致使风机塔筒发生剧烈的振动，大大降低风机的发电效率，甚至导致结构发生疲劳破坏，严重威胁结构的安全。黄焱等[13]率先对渤海单柱三桩式海上风机的冰激振动问题进行了研究，建立了基于综合控制因子的冰振事件区划及概率预判方法；叶柯华等[14]基于强迫振动原理，研究了风冰联合作用下海上风机的振动响应。这些现存的文献主要关注冰-结构相互作用的机理，而对发生锁频时，如何有效的避免或控制结构的振动研究较少，特别是对新兴的海上风电结构。

在结构振动控制领域，目前常用的控制方法包括被动控制、半主动控制以及主动控制[15]。文献[16]采用被动式调谐质量阻尼器(TMD)研究了冰区海洋石油平台的振动控制问题；文献[17]提出了半主动式冰锥结构用于进一步缓解锥体冰载引起的结构振动；许多学者利用不同阻尼器亦开展了海上风机结构的振动控制研究[18-22]，但分析载荷限于风、波和地震，而针对海冰载荷下的振动控制却鲜有文献报道。海冰运动主要取决于海流和海风，实现中，其运动方向往往与风载荷成一定夹角，在冰和风二者联合作用下，风机塔筒在叶片旋转平面内(面内方向)和平面外方向(面外方向)均会发生不同程度的振动，因此，需要对塔筒同时进行面内和面外振动控制。文献[23]提出了一种三维摆式阻尼器，验证了其相对于常规TMD具有明显的优势，且更适用于在多种载荷非同向作用时的振动控制。为此，本文针对NREL 5 MW海上单桩风机，基于Määttänen-Blenkarn模型原理，采用ANSYS参数化设计语言，开发海上风机自激振动分析程序，分析NREL 5 MW风机在冰区海域的锁频振动问题，并将三维摆式阻尼器应用于该风机的冰激振动控制中，研究其对冰区海上风机振动响应的控制效果，以期为我国大型风机在冰区海域的投产与运行提供技术支持。

1 冰区风机动力平衡方程

位于冰区的海上风机，冬季海平面结冰时，主要遭受风、流和海冰载荷的联合作用，其动力平衡方程可表示为

FT(t)+FI(t)+FC(t)

(1)

2 动冰载荷

2.1 自激振动原理

目前，针对海冰引起的结构动力问题，国内外学者提出了多种冰-结构相互作用模型。概括而言，可将其分为强迫振动和自激振动两大类别[24]。其中，自激振动理论被广泛应用于海洋工程结构冰激振动分析中[25]。该模型基于冰体连续破坏假设，充分考虑了海冰抗压强度与应力速率的关系，如图1所示。

图1 海冰抗压强度与应力速率关系Fig.1 Ice crushing stress vs.stress rate with different interaction regions

该曲线将冰与结构相互作用划分为三个典型的区域：(1) 低冰速延性区，冰排发生延性挤压破坏，结构响应为准静态；(2) 中冰速延性-脆性转换区，结构发生稳态振动，响应最大；(3) 高冰速脆性区，冰排发生脆性挤压破坏，结构响应为随机振动。自激振动模型认为在延-脆转换区内，由于海冰抗压强度随冰力加载速率的增大而降低，从而导致了负阻尼效应，当该负阻尼大于结构阻尼时，会导致结构振动趋于较大的稳态振动，即发生锁频振动。

2.2 Määttänen-Blenkarn模型

基于实测数据，Määttänen-Blenkarn给出了海冰抗压强度与应力速率的多项式表达式[25]，即

(2)

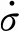
(3)

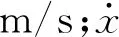
动冰载荷则可表示为海冰抗压强度与作用面积的乘积，即

(4)

由于海冰载荷是风机结构响应速度的函数，因此式(1)为需要编程进行迭代计算。整个计算分析的流程图，如图2所示，其中气动风载荷的生成详见本文第3章。

图2 程序求解流程图Fig.2 The flow chart of programming

3 空气动力载荷

不同于海洋平台结构受力特点，海上风机依靠巨大的叶片将空气动能转化为机械能，因而，其风载荷所占的水平侧向载荷比例较大，是其动力分析的重要载荷之一。

3.1 湍流风场模型

海上风机受到的风速可表示为平均风速和脉动风速之和。其中，任意高度z处的平均风速可采用对数或指数型式风剖面计算。采用对数风剖面型式时，则有

(5)

式中:v(z)为高度z处的平均风速，m/s；v0为参考高度H处的平均风速，m/s；H为风机轮毂处高度，m；z为距海平面的高度，m；z0为粗糙度长度，m，对于海平面，取0.03 m。

脉动风速则可采用IEC卡曼谱[26]进行描述，即

(6)

式中:Sv(f)为脉动风速的功率谱密度函数；f为频率，Hz；LC为积分尺度参数；I为湍流强度；v为风速，m/s。

考虑风速的空间相干性，任意计算两点i和j的互谱Sij可表示为

(7)

式中:Sii和Sjj分别为计算点i和j处的自功率谱；L为计算点i和j之间的距离，m；a0为相干性衰减系数；vH为轮毂处的平均风速，m/s；其余参数同上。根据IEC-1 1th推荐数值，本文取a0=12，LC=340.2 m。

根据式(5)～式(7)，基于TurbSim程序生成风机叶轮处的三维风场[27]，采用31×31的网格对整个风机扫掠面积的风场进行离散，然后利用MATLAB开发的程序得到作用于叶轮每段微元上的风速分布。

3.2 风机叶片载荷

将风机叶片沿展向离散为N个微元，假设每个微元之间互不影响，根据动量理论可推导作用于每段微元上的空气推力和转矩，采用叶素动量理论即可计算旋转叶片上的空气动力载荷[28]。

取任意第i个叶片微元分析，如图3所示，相对来流风速vr可以表示轴向风速v(1-b)与切向风速Ωr(1+b′)的矢量和，即

(8)

(a) 叶片微元

式中:b和b′分别为轴向和切向速度诱导因子；r为微元距离轮毂旋转中心的半径，m；Ω为叶轮的转速，rad/s。

于是，作用于每个叶素上的升力dFL和阻力dFD可以表示为

(9)

式中:c(r)为叶素弦长，m；CL和CD分别为升力系数和阻力系数；dr表示叶素长度，m；vr为相对于每个叶素的来流速度，m/s；ρ为空气密度，kg/m3。

根据几何关系，可以推导每个叶素上的轴向力和切向力为

dPN=dPLcos φ+dPDsin φ

dPT=dPLsin φ-dPDcos φ

(10)

式中:φ为相对来流风速vr与叶片旋转平面的夹角，φ=a+θ，其中，a为风攻角；θ为翼型扭转角。

由于轴向和切向速度诱导因子b和b′为非已知参数，采用式(8)～式(10)计算叶片风载荷时，需要通过迭代进行求解。为此，本文基于MATLAB开发了风机叶片轴向和切向风载荷时程的计算程序，并考虑了Prandtl叶尖损失修正和Grauert修正。图4展示了风速为12 m/s，湍流强度为0.1时，计算得到的NREL 5 MW风机单个叶片上的风载荷时程。

图4 叶片轴向风载荷与切向风载荷时程Fig.4 Normal and tangential aerodynamic loading applied on the blade

4 分析模型

4.1 5 MW风机参数

采用NREL 5 MW海上单桩风机作为分析对象，目标海域水深为20 m，桩基入泥深度36 m，塔筒总高90 m，过渡段距海平面高层为10 m，其基本尺度如图5所示，其他参数详见表1。将摆式阻尼器置于塔筒顶部，如图5(a)所示。采用ANSYS软件建立该风机振动响应分析模型，如图5(b)所示，其中，风机叶片基于NREL 5 MW提供的刚度数据采用BEAM4单元进行等效模拟；机舱和轮毂等效为无密度刚性梁单元，其重量则采用MASS2进行模拟(分别为240 t和56.78 t)；塔筒采用BEAM188单元的变截面锥形梁模拟；单桩支撑结构采用PIPE59单元模拟；桩土相互作用则采用文献[29]的方法，采用等效刚性梁和弹簧阻尼单元COMBIN14进行模拟，其中刚性梁等效长度取7.6 m，水平弹簧刚度为3.89×109N/m，转动弹簧刚度为1.14×1011N·m/rad，转动阻尼为9.34×108N·m·s-1/rad。

(a) 5 MW风机

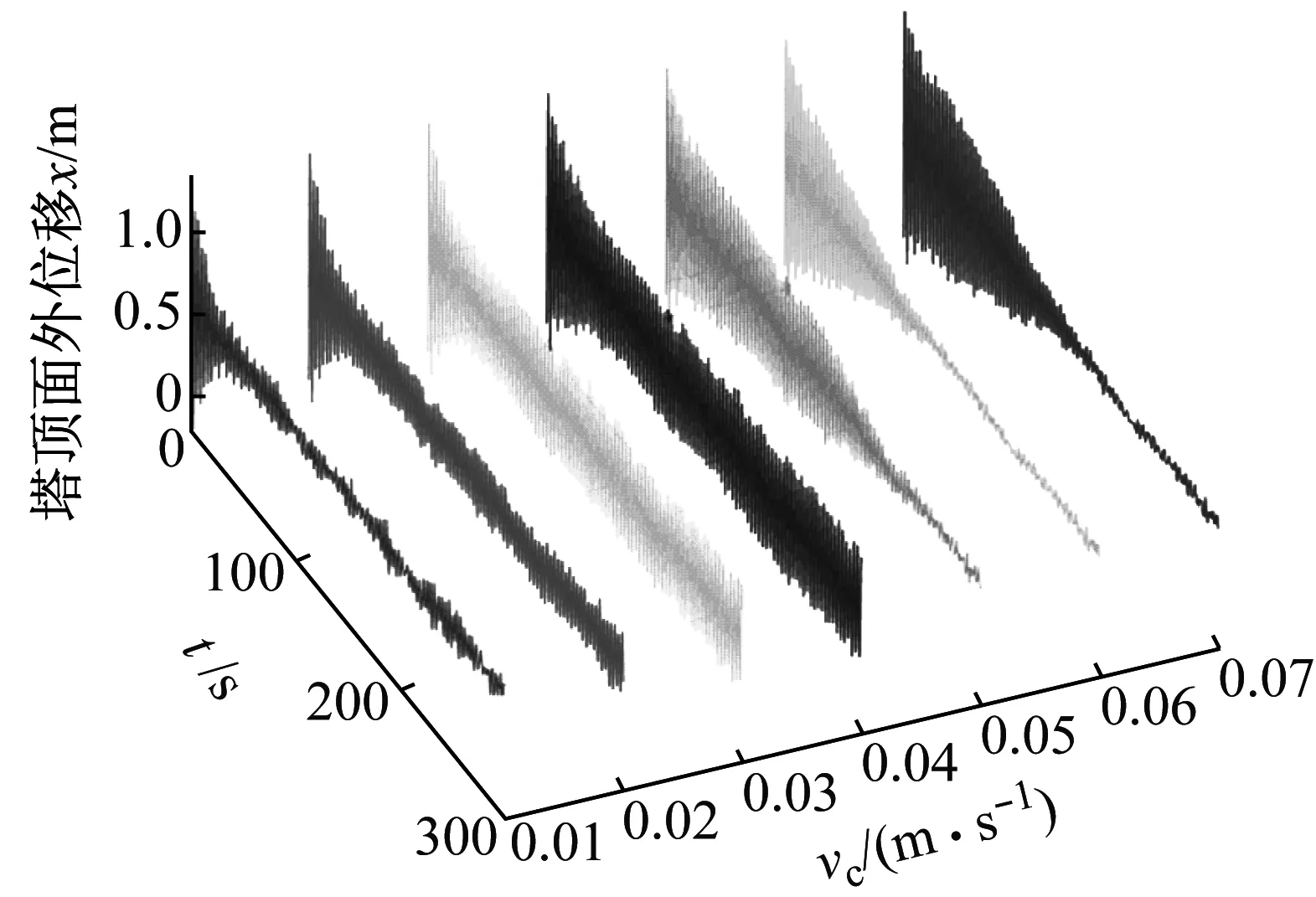
(a) 面外位移

(a) vc=0.01 m/s

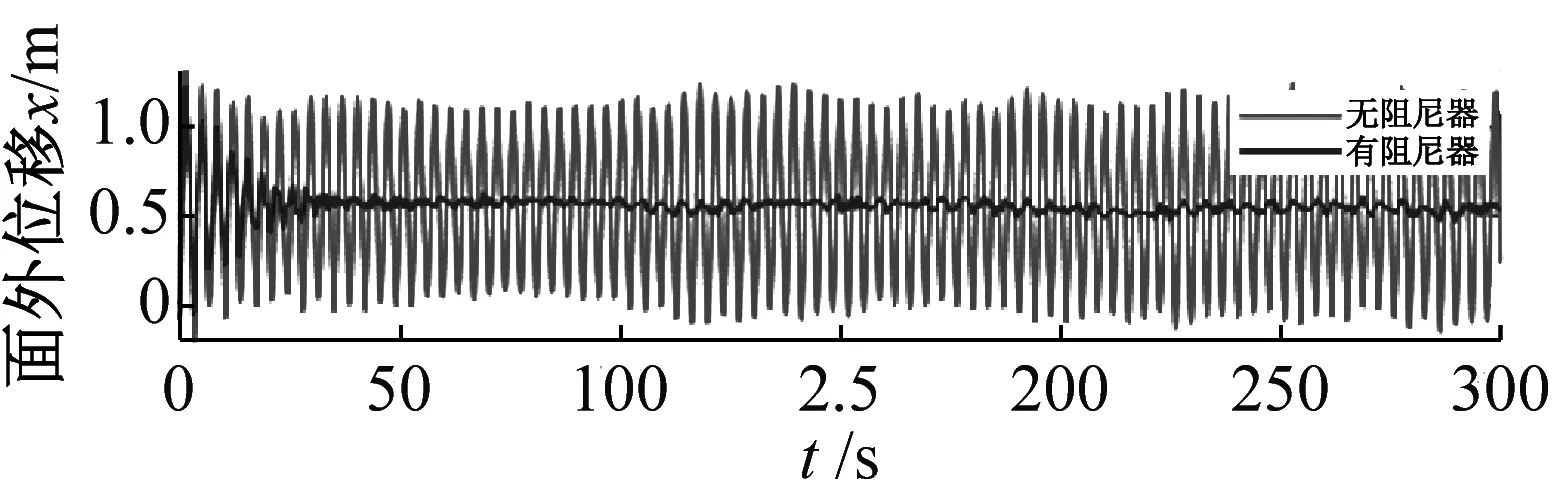
(a) 工况1 vc=0.06 m/s

(a) 面外方向

(a) 面外位移峰值

表1 5 MW海上风机基准模型参数Tab.1 Parameters of the NREL 5 MW baseline wind turbine

4.2 特征频率

采用Block Lanczos法对该风机进行模态分析，求得其整体模型自振频率，并与FAST软件计算结果进行对比，如表2所示。

表2 模态对比结果Tab.2 Comparison between the finite element model and FAST

由表2可知，本文所建立模型的模态分析结果与FAST分析结果具有较好的一致性，但数值略小于FAST分析结果，其原因主要是边界条件不同所致(文中模型考虑了土壤边界约束，而FAST结果为固支约束条件下所得)。

4.3 摆式阻尼器参数

采用三维摆式阻尼器对该风机在海冰载荷下的振动响应进行控制，需要确定阻尼器的最优参数，包括质量、最优阻尼比以及最优频率比。基于文献[23]的研究成果，三维摆式阻尼器的最优频率比fo以及最优阻尼比ζo的计算式为

fo=7.6μ2-2.5μ+1

ζo=-2.7μ2+μ+0.062

(11)

式中，μ为质量比，定义为阻尼器质量与风机结构总质量(不包含下部支撑结构和桩基部分)之比。

取质量比μ为2%，由式(11)求得fo=0.95，ζo=0.081；基于风机模态分析结果，求得摆式阻尼器的频率fp为0.274 4 Hz，进而确定其摆长为3.27 m，阻尼为3 895.5 N·s/m，质量为13.9 t。在ANSYS有限元模型中，采用质量单元MASS21、LINK188以及COMBIN14单元分别模拟三维摆式阻尼器的质量、摆长和阻尼，即可建立带阻尼器的分析模型，从而分析三维摆式阻尼器的减振效果。

4.4 分析工况

以我国渤海海域某风电场现场实测统计参数，对NREL 5 MW风机的锁频振动响应进行分析。该海域海冰抗压强度为2.0 MPa，弯曲强度约为0.68 MPa，1年一遇平整冰厚为7 cm，50年一遇冰厚为32 cm。考虑1年一遇海冰环境条件，对该冰厚下不同冰速以及不同环境载荷组合角度下的风机振动响应进行分析，以确定锁频发生的载荷工况。计算时，取风速为12 m/s，湍流强度为10%，风攻角保持垂直于风机叶片旋转平面，即与x轴夹角为0°；海流剖面取线性剖面，表层流速取与冰速一致，底层流速为0 m/s，考虑4种不同的环境载荷组合方向，见表3。

表3 风冰流载荷组合方向Tab.3 Multi-direction combined of wind,ice and current load

5 结果分析

5.1 无阻尼器风机振动锁频分析

采用APDL开发基于Määttänen-Blenkarn模型的自激振动分析程序，取载荷步长为0.01 s，计算时长为300 s，针对表3中不同工况中等冰速进行搜索(冰速从0.01 m/s开始试算，每次增加0.01 m/s，直至冰载表现为脆性特征)，得到不同冰速下风机塔筒顶部的面内(x-z平面)和面外位移(y-z平面)响应，如图6所示(限于篇幅，以工况2为例)。

由图6可知，工况2下，即风攻角为0°，冰攻角为30°时，风机塔顶面外位移响应远大于面内响应；当冰速为0.01 m/s，风机塔顶面内和面外位移振幅较小，表现为准静态响应；随着冰速的增加，当冰速为0.02 m/s、0.03 m/s、0.04 m/s，塔顶面外位移在50 s后表现为稳态响应，塔顶面内位移则表现为典型的共振特性，即发生锁频振动，此时，风机塔顶振幅远大于其他冰速下的响应，且随着冰速的增加，其响应幅值逐渐增大，最大稳态面外位移达0.93 m，最大面内位移达0.35 m，显然，会影响风机的平稳发电；当冰速相对较大时，即0.05 m/s和0.06 m/s时，随着结构响应的衰减，海冰与风机结构相对速度增大，冰载荷降为较小值，塔顶响应最终趋于小幅振动，在稳态响应阶段受冰载荷的影响较小。

进一步去除瞬态分析初始效应的影响，取计算时间200 s后的风机塔筒顶部水平位移结果，对其进行傅里叶变换，分析其频域特性，并与相应的冰载频域特性进行对比，如图7所示。

由图7可知，当冰速为0.02 m/s、0.03 m/s、0.04 m/s时，风机塔筒振动主频为0.28 Hz，略小于其结构一阶频率0.289 Hz(这与文献[30]在实验中发现的规律一致)，而此时，对应的冰力频率亦在风机结构基本以及倍频上出现峰值，即发生一阶锁频振动；当冰速低于0.02 m/s时，冰载荷与塔筒位移的主频率为0.27 Hz，小于其一阶基频；冰速为0.05 m/s，风机位移响应主频为0.29 Hz，而冰载荷主频率则演变为1.45 Hz；当冰速为0.06 m/s，风机振动主频与风机叶片转频为0.2 Hz一致，即其振动响应主要受叶片运行及其风载荷控制，此时，冰载荷主频比冰速为0.05 m/s时略有增大，变为1.48 Hz。综合风机位移响应可知，工况2时，风机在冰速为0.02～0.04 m/s时，发生一阶锁频振动，此时振动响应最大，而非锁频时，风机振动位移相对较小，运行平稳，且在冰速大于0.05 m/s，冰载荷主频跳跃为高频，逐渐远离风机基频，向脆性区演变，冰载荷演化为风机振动的次要控制载荷。

表4给了其他工况下风机塔筒在计算时间200～300 s内的水平合位移响应最大幅值，以及发生锁频事件所对应的冰速。由表4可知，当海冰与风攻角相同时，发生一阶锁频事件对应的冰速范围最大，为0.02 m/s～0.06 m/s，且由于两种载荷的组合叠加效应，风机位移响应振动最为剧烈，在冰速为0.06 m/s时，风机位移幅值达到1.424 m，严重威胁风机运行安全；随着冰-风载荷夹角的增大，锁频事件对应的冰速范围有所降低，风机位移响应幅值总体亦呈降低趋势，当海冰方向为90°时，风机振动响应最小，发生锁频时的最大幅值位移降为0.76 m。

表4 风机塔筒水平位移振动幅值Tab.4 Horizontal displacement amplitude at tower top

5.2 三维摆式阻尼器振动控制评价

以4种环境组合工况中风机振动响应最大时的冰速为例，展示三维摆式阻尼器对风机冰激振动响应的控制效果，如图8所示。

由图8可知，工况1时，即冰-风同向时，三维摆式阻尼器对风机塔筒面外振动响应起到极佳的控制效果，稳态响应的振动幅值减小可达90%；但在面内方向，仅在初始振动阶段存在一定控制作用，当计算时间大于100 s后，部分时刻存在缓解振动的作用，部分时刻使风机振动略有增加，但应注意到，由于该工况风机面内载荷主要源自叶片的风载，因此，其面内位移振动很小，最大值不足0.2 m。工况4时，即当冰-风夹角为90°，三维摆式阻尼器在面内(冰载作用方向)起到良好的减振效果，在面外方向，则使得风机振动快速衰减至振动微小的稳定响应；当冰-风夹角为30°和90°时，摆式阻尼器在起到双向控制作用，在面内和面外均大大降低了风机塔筒的振动响应。

图9展示了工况2下，冰速为0.04 m/s时有无3D-PTMD的风机塔顶面外和面内方向振动位移的频率响应图。由图9可知，安装3D-PTMD后，风机塔顶面外和面内的峰值频率能量均被大大降低，3D-PTMD具有极佳的耗能效果；尤其在面内方向，3D-PTMD使得风机塔顶的面外峰值频率由0.28 Hz调谐至0.2 Hz，减振动效果非常显著。

计算表4中所有工况有、无3D-PTMD的风机塔筒响应峰值及标准差，进一步量化三维摆式阻尼器对风机振动控制的效果，如图10所示。

由图10可知，三维摆式阻尼器大大降低了风机塔筒顶部位移的峰值和标准差，面外方向最大分别降低为51.8%和93.7%，面内方向最大分别降低62.8%和84.2%，对风机塔筒的振动响应起到极佳的控制效果。由图10(b)和10(d)可知，在面内振动风向，三维摆式阻尼器对部分计算工况存在负面影响，但这些工况主要为非锁频工况，此时的风机振动响应均相对较小(如工况2中冰速为0.06 m/s时，位移峰值和标准差分别放大6.4%和13.5%，而由图6可知，该工况风机稳态响应时的面外和面内位移振幅仅为0.141 m和0.096 m)，即三维摆式阻尼器的负面影响并不会干扰风机的正常运行。

6 结 论

基于自激振动原理，开发冰区风机振动分析程序，实现对NREL 5 MW海上单桩风机锁频振动的有效模拟，并对其振动响应进行控制，结果表明：

(1) 针对1年一遇冰情，综合不同环境组合工况结果，该风机发生冰激锁频现象的冰速范围为0.01～0.06 m/s；海冰作用方向对锁频事件的发生具有明显的影响，当冰-风载荷同向时，对应的锁频冰速范围最大，更易发生锁频事件，当冰-风非同向时，锁频所对应的冰速范围变窄。

(2) 发生锁频时，随着冰速的增加，风机塔筒振动响应逐渐增大，冰-风同向时，最大面水平振动幅值达1.424 m，即在常遇海冰作用下，一旦发生锁频振动，风机结构的运行安全性将受到严重威胁；冰-风非同向时，塔筒振幅降低，当冰-风为90°夹角时，振动响应最小。

(3) 三维摆式阻尼器可以对风机锁频振动响应起到极佳的控制效果，增加三维摆式阻尼器后，风机塔筒顶部面外和面内振动响应峰值和标准差均得到有效的抑制，在部分非锁频工况，三维摆式阻尼器存在负面效应，但影响甚微，综合而言，在进行冰区海上大型风机安装时，可以增设三维摆式阻尼器，以实现对风机振动响应的控制，提高风机运行的疲劳寿命。