基于支持张量机的近红外光谱检测成品纸张质量
杜树新,裘 一
(湖州师范学院 工学院,浙江 湖州 313000)
0 引 言
成品纸张的质量指标是衡量纸张质量的重要因素,包括水分(纸产品中含有的水量)、灰分(纸经高温灼烧后剩下残留矿物质与原来质量之比)、克重(每单位面积纸的质量,也称纸张定量)、厚度、机械浆和化学浆含量等.作为无损、快速的检测技术,近红外光谱在纸张质量检测中受到越来越广泛的关注[1-3].
近红外光谱曲线在数学上表现为向量形式,一般采用主元回归、偏最小二乘、神经网络及支持向量机等基于向量形式的方法建立校正模型.在基于向量形式的建模方法中,向量长度与建模中需要确定的模型参数相关.一条近红外光谱曲线一般有成百上千个光谱数据点,如果采用向量形式的方法建模就需确定成百上千个模型参数,这就意味着需要大量的训练样本[4].而在小样本情况下,由于训练样本较少,容易导致欠拟合,校正模型的精度达不到理想要求.
支持张量机是近年来发展起来的、适用于张量数据的机器学习方法,是支持向量机方法在张量形式上的进一步扩展.支持张量机中需要确定的模型参数数量是张量数据的维数之和.以二阶张量X∈Rn1×n2为例,其模型参数数量为n1+n2.如果将一个长向量(长度为n)通过某种方式组装成一个n1×n2的二阶张量(n≈n1×n2),那么需要确定的模型参数数量就由n下降为n1+n2,这样也降低了对训练样本数量的要求.
本文将采集的成品纸张近红外光谱的向量数据组装成二阶张量数据,再采用支持张量机方法进行建模,实现对成品纸张质量的检测,并对双面铜版纸进行实验研究.将向量数据组装成二阶张量数据,可使待确定的模型参数数量显著减少,从而显著降低对训练样本数量的要求,提高小样本校正模型的检测精度.
1 实验方法
1.1 将大长度的向量组装成二阶张量
假设将向量x∈Rn组装成二阶张量X∈Rn1×n2,即根据n确定n1和n2的值.假定n1≥n2,为保证在组装二阶张量时拥有至少n个元素,n、n1、n2需要满足(n1-1)×n2 根据优化得到的n1和n2,将n个元素的向量x填充到n1×n2的二阶张量X中.具体方法为:将x中的前n1个元素放在张量X的第1列,下一组n1个元素放在张量X的第二列,以此类推.对剩余没有被填满的位置,用任意值进行填充.图1是将长度为11的向量组装成4×3的二阶张量. 图1 将长度为11的向量组装成4×3的二阶张量Fig.1 The vector of length 11 assembled into a 4 × 3 second order tensor 支持张量机方法是支持向量机扩展到张量模式的一种监督学习方法,由Tao等于2005年首次提出并应用于分类预测问题,2012年Guo等将分类预测扩展到回归预测[4],从而可应用于光谱的定量分析.由于所组装的张量为二阶张量,可直接采用文献[5]中N阶张量的支持张量机方法.为便于理解,本文简单给出二阶张量的支持张量机方法. 给定训练样本及输出{Xi,yi},i=1,2,…,M,其中Xi∈Rn1×n2为输入的、经组装成二阶张量的近红外光谱数据;yi∈R为输出的目标值即纸张质量指标;M为训练样本数量.所构造的回归估计函数(校正模型)为: f(X)=uTXv+b, (1) 其中,u∈Rn1、v∈Rn2、b∈R为模型待定参数.由此看出,待定的模型参数数量为n1+n2+1.类似于支持向量机方法,引入ε不敏感损失函数,将回归函数的确定转化为如下优化问题[5]: (2) 步骤1:初始化向量u,如u的所有元素值为1. (3) 这是标准的支持向量机形式.其可采用支持向量机中的二次规划方法,即拉格朗日乘子法求解该优化问题[4],即求得向量v. (4) 这是标准的支持向量机形式,可经同样的计算得到u. 步骤4:循环执行步骤2和步骤3,直到本次循环得到的u∈Rn1、v∈Rn2、b∈R与上次循环得到的值充分接近.达到最优化后,根据所计算的u、v和b,由式(2)得到回归模型,即校正模型. 由某纸业公司品管部技术人员对双面铜板纸的水分、灰分、克重和厚度进行检测,并采用布鲁克公司的傅里叶近红外光谱仪(Bruker Equinox 55)采集近红外光谱数据(波长为800~2 500 nm;光谱数据点为2 203个).为确保数据的正确性,每个样品重复检测3次,取平均值,共采集816个双面铜版纸样本. 光谱预处理的目的是消除原始光谱中仪器噪声、背景漂移及测量干扰等的影响,预处理的方法包括消除噪声、基线校正及归一化等. 实验中训练集和测试集的样本大致按4∶1的比例随机抽取,训练集的样本数为652个,测试集的样本数为164个. 光谱经过预处理后,首先根据相关系数分析法选取相关系数较大的光谱点组成向量.然后按照1.1节的方法组装成二阶张量,位数不足的用0补全.水分选取2 444~2 481 nm共35个波长点组装成6×6的二阶张量;灰分选取2 348~2 381 nm共30个波长点组装成6×5的二阶张量;厚度选取2 441~2 484 nm共45个波长点组装成7×7的二阶张量;克重选取2 431~2 484 nm共50个波长点组装成8×7的二阶张量.最后使用支持张量机方法对组装成的二阶张量进行建模,对水分、灰分、克重、厚度等独立建模.图2至图5分别为测试样本的水分、灰分、厚度、克重等质量参数与实际值的相关性图.从图中可见,采用支持张量机方法建立的校正模型检测效果较理想. 图2 水分检测的相关性Fig.2 Correlation of moisture 图3 灰分检测的相关性Fig.3 Correlation of ash 图4 克重检测的相关性Fig.4 Correlation of gram per square meter 图5 厚度检测的相关性Fig.5 Correlation of thickness 为进行比较,采用主元回归(PCR)、偏最小二乘(PLS)、支持向量机(SVM)等基于向量的方法建立校正模型,并对双面铜版纸质量参数进行预测.表1为这3种方法与支持张量机方法(STM)建立的模型性能比对结果(支持向量机采用高斯核函数).评估模型性能的指标为相关系数和预测误差均方根,相关系数越接近1,预测误差均方根越小,说明模型性能越好.从表1可看出,支持张量机方法相比主元回归、偏最小二乘、支持向量机等方法,相关系数和预测误差均方根都有一定改善,其原因是支持张量机中待确定的参数数量较少. 表1 采用PCR、PLS、SVM、STM等方法建立的模型性能比较 将向量形式的近红外光谱数据表示成二阶张量形式进行,再采用支持张量机方法建立校正模型,其目的是解决小样本情况下的欠拟合问题,因此需要对不同样本数量建立的模型性能进行考察.实验样本数由10逐渐增加到816,并采用留一验证法评估模型的性能.图6至图9分别为当样本数由10到816变化时,通过支持向量机方法与支持张量机方法所建模型来预测水分、灰分、克重和厚度的相关系数和预测误差均方根的变化情况.从图中可以看出,样本数较少时,采用支持张量机方法建立的模型性能优于支持向量机方法;随着样本数的增加,两种方法建立的模型性能渐渐趋向一致(除灰分和厚度的预测误差均方根外,其他质量参数均保持较固定的差距).换言之,样本数较少时,支持张量机方法建立的模型性能优于支持向量机方法;样本数较多时,两者差异不大,即对小样本问题,采用支持张量机方法建立的模型预测效果优于支持向量机方法. 图6 水分的模型性能随样本数量变化情况Fig.6 The change of moisture model performance with the number of samples 图7 灰分的模型性能随样本数量变化情况Fig.7 The change of ash model performance with the number of samples 图8 克重的模型性能随样本数量变化情况Fig.8 The change of model performance for gram per square meter with the number of samples 图9 厚度的模型性能随样本数量变化情况Fig.9 The change of thickness model performance with the number of samples 本文将采集的成品纸张近红外光谱的向量数据组装成二阶张量数据,再采用支持张量机方法进行建模,实现对成品纸张质量的检测移正.该方法减少了模型参数的数量,降低了对训练样本数的要求,更适合小样本校正模型的建立.采用校正模型对双面铜版纸的水分、灰分、克重和厚度等质量指标进行检测,结果表明,采用支持张量机方法建立的校正模型,其相关系数、预测均方根误差等性能指标优于基于向量的主元回归、偏最小二乘、支持向量机等方法建立的模型.实验还研究了训练样本数量与模型性能的关系,结果表明,随着样本数的增加,采用支持向量机方法建立的校正模型,其性能逐步增加,两种方法建立的模型性能差距逐渐减少;在小样本情况下,支持张量机方法建立的校正模型,其相关系数、预测误差均方根明显优于基于支持向量机方法建立的模型.由此说明,本文采用支持张量机方法建立的校正模型更适宜小样本.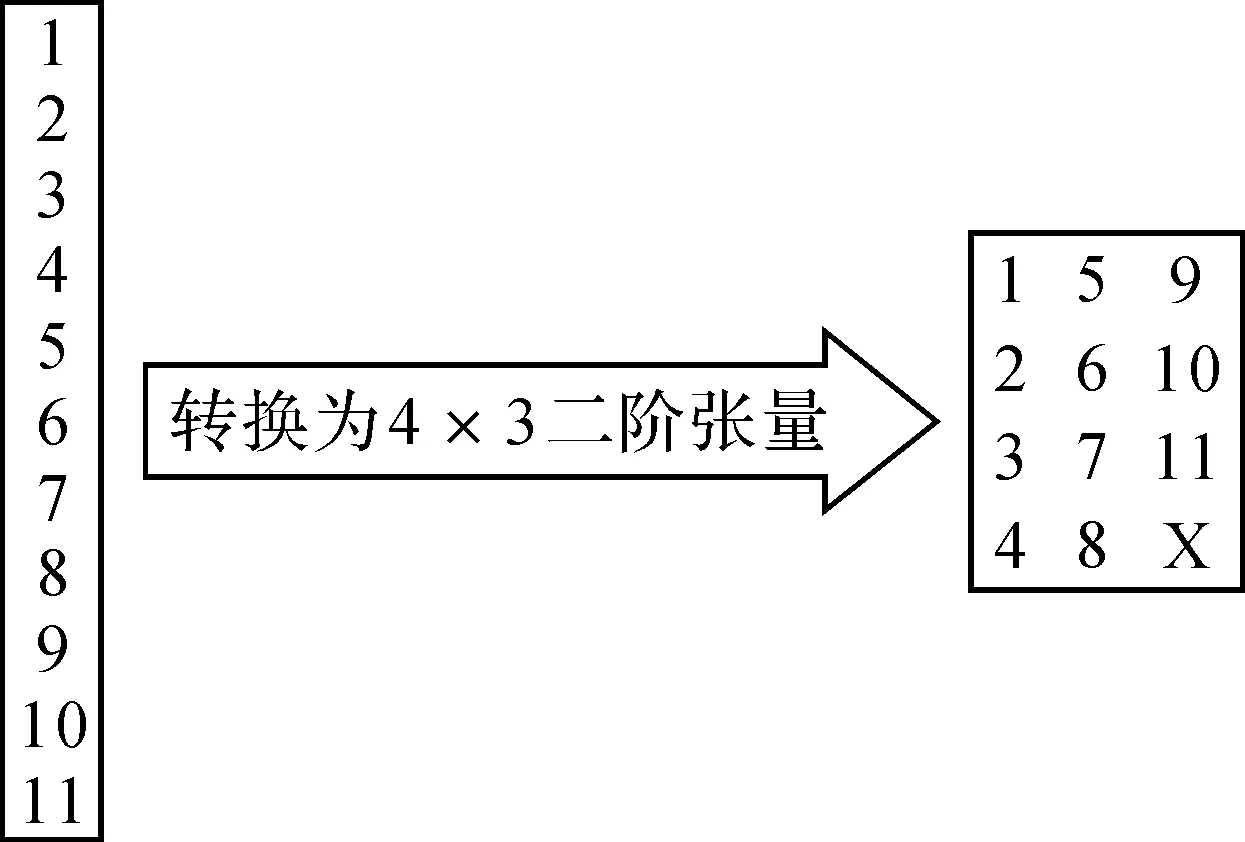
1.2 二阶张量的支持张量机方法




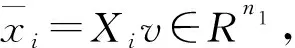

2 结果与分析
2.1 纸张质量数据、近红外光谱数据的采集
2.2 近红外光谱数据的预处理
2.3 采用支持张量机方法建立校正模型的实验结果




2.4 与其他建模方法的比较

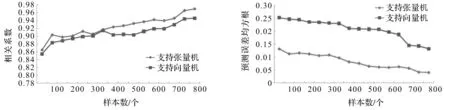
2.5 实验样本数对模型性能的影响



3 结 论

