李级数法在两体问题中的应用
肖志峰,林文斌
(南华大学 数理学院,湖南 衡阳 421001)
0 引 言
广义相对论最重要的应用之一是理解时空曲率对天体运动的影响[1]。广义相对论描述了牛顿力学框架下所不能描述的宇宙大范围的行为,开启了天体物理全新的研究领域。在爱因斯坦的广义相对论中[2],时空是一个四维的伪黎曼流形,物质与时空的相互作用是非线性的,因此一般而言,广义相对论的计算是非常复杂的,这也使得对广义相对论的理解更加困难。
基于上述原因,爱因斯坦等人在二十世纪三十年代发展了一种摄动方法,能够描述广义相对论对太阳系中的天体演化所引起的细微变化,A.Einstein、L.Infeld、B.Hoffmann[3]在1938年得到的结果就是一阶后牛顿(1PN)的结果,这也标志着“相对论天体力学”这一新领域的诞生。此后,相对论天体力学的研究一直方兴未艾,对后牛顿展开进行了大量不同的分析,同时提出了许多新的更有力的工具来研究相对论天体力学[4-5]。尽管相对论天体力学取得了长足的进步,但得到后牛顿展开的解析仍然是一项艰巨的任务。特别是,到目前为止,轨道运动和旋转运动之间的相互作用还没有得到足够的研究。
本文着重研究了带自旋双星的运动问题的二阶后牛顿(2PN)展开,目标是基于李级数摄动理论[6-7]得到一个运动粒子的轨道角动量的z分量关于时间t演化的解析解,这个方法可以得到系统的长期演化行为,并且可以拓展到更高阶的后牛顿近似展开。
1 哈密顿量
本文的推导从自旋双星问题的2PN哈密顿量开始。在折合质量与折合质量坐标系中,自旋双星问题的2PN哈密顿量为[8]
H=HN+εH1+ε2H2
(1)
这里ε=1/c2是选择的一个小参数,其中c表示光速。在摄动理论中
(2)
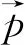
(3)
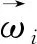
H1的表达式为
H1=HPN+HSO+HSS,
(4)
这里
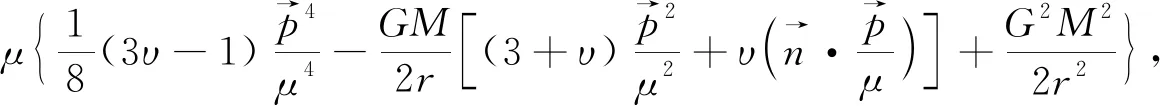
(5)
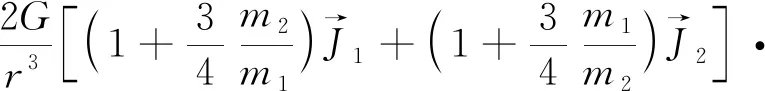
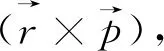
(6)
是轨道-自旋相互作用项,且
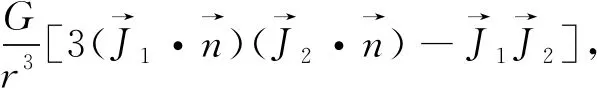
(7)
是自旋耦合作用项。
H2的表达式为
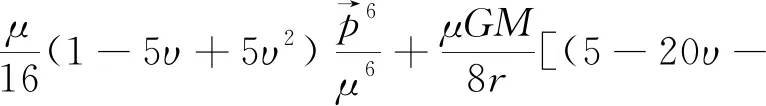
(8)

(9)
(10)
(11)
(12)
(13)
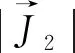
(14)
2 作用角变量
为了使用李级数摄动法来研究哈密顿量式(9)~式(13),我们需要将哈密顿量表示在作用角变量坐标中的摄动形式。对于轨道运动变量,一般选择Delaunay元素集来表示。而对于旋转运动变量,一般选择Serret-Aadoyer(SA)变量。这两组变量都是正则变量。
对于Delaunay元素集,可以通过以下标准关系来引入[10]
H=Gcosih=Ω
(15)
这里a是轨道半长轴,e是轨道偏心率,i的轨道倾角,ω是近心点幅角,M是平近点角,Ω是升交点黄经。L是半主轴的归一化平方根,G是轨道角动量的归一化,H是轨道角动量的归一化的z分量。在方程中,(L,G,H)表示广义动量,(l,g,h)表示广义坐标。
SA变量[11]是描述一个刚体关于旋转角和旋转角动量的相互关系。在讨论中,物体是一个理想的球体,所以SA变量的形式可以表示为
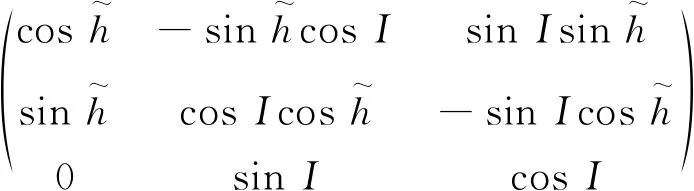
(16)
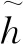
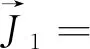
(17)
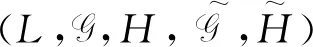
(18)
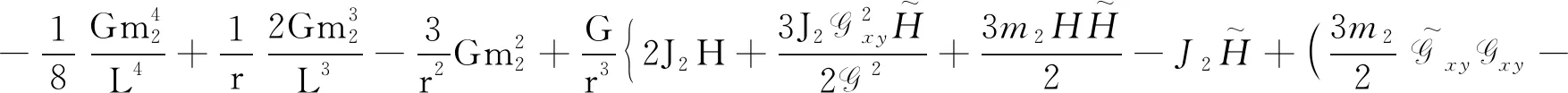
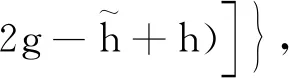
(19)
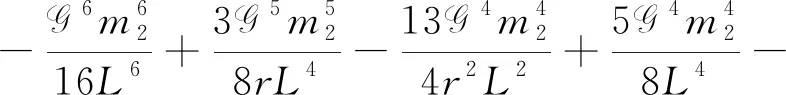
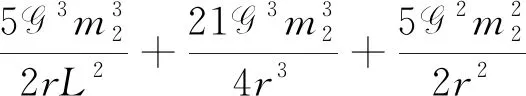
(20)
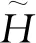
r=r(L,G,l),
(21)
Gxy=Gxy(G,H),
(22)
(23)
f=f(L,G,l)。
(24)
现在可以使用李级数[6-7]来分析哈密顿量。李级数扰动方法的目的是通过坐标的拟正则变换来简化问题的哈密顿量,这个变换取决于生成函数χ。李级数变换如下
(25)
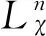
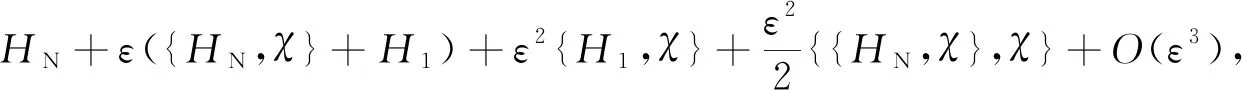
(26)
因此需要解同态方程
{HN,χ}+H1=K。
(27)
(28)
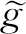
(29)
在方程中,其本质表为平近点角的运动,因此,通过李级数变换且在方程中确定了χ后,哈密顿量变为如下形式
(30)
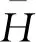
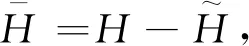
(31)
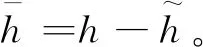
(32)
通过式(31)、式(32)的变换后,最终形式的哈密顿量为
(33)
这里F0、F1、F2仅仅是动量的函数
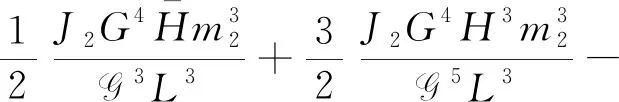
(34)
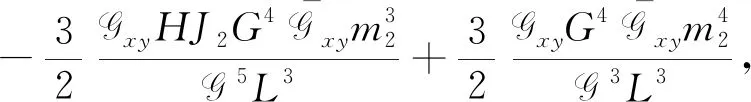
(35)
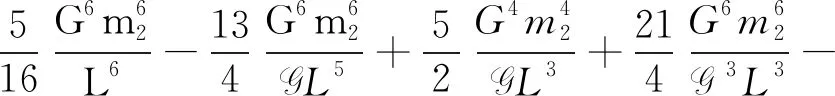
(36)
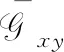
(37)
现在可以来分析最终形式的哈密顿量了。首先将哈密顿量代入正则方程得到的运动方程为
(38)
和
(39)
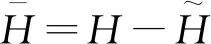
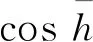
将方程和方程中关于H的方程
(40)
结合起来,可以得到
(41)
这里H′是哈密顿常数。通过计算,可以证明,方程(41)中右边关于H5和H6的项都抵消了。因此方程(41)的右边是一个关于H的四次多项式[12],即
f4(H)=ε2F12-(H′-HN-εF0-ε2F2)2=a0H4+a1H3+a2H2+a3H+a4,
(42)
其中a0,a1,a2,a3,a4是代入各项后整理得到的系数。重写方程为
(43)
这里H0是H的初始值,t0是初始时间。除符号外,方程的左边是标准的椭圆积分。通过Weierstrass公式[12],可以写为
(44)
这里a是一个任意常数,于是有
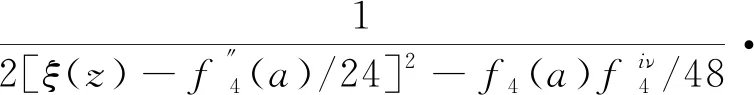
(45)
这里ξ(z)≡ξ(z;g2,g3)定义为关于不变量g2、g3的Weierstrass椭圆函数
(46)
其中f4的导数表示关于变量H的导数。H关于时间t的演化方程的解为
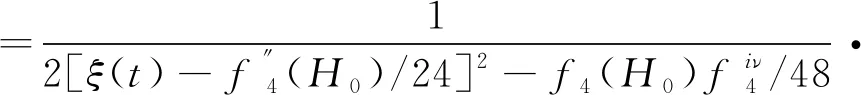
(47)
3 结 论
在本文中,文章基于李级数摄动理论分析了带自旋双星问题的演化。基于李级数摄动理论,得到了椭圆函数形式的解析解,从而可以分析系统的长期扰动效应,这是用数值方法所不能做到的。这个方法也可以推广到更高阶的后牛顿展开,以得到更精确的结果。

