高效无源三次倍频器研究与设计
孙 毅,王 彦
(南华大学 电气工程学院,湖南 衡阳 421001)
0 引 言
随着通信技术的发展,所使用的信号频率越来越高,目前5G已经采用了毫米波[1],因此对于毫米波甚至是太赫兹频段的研究成为当前的热点。毫米波频率源由于频率较高,通常采用低频频率源与倍频器级联的方式制作频率源,因此毫米波倍频器具有重要的研究意义。中国空间电子信息技术研究院的研究人员基于肖特基势垒二极管,通过波导腔体结构进行精细仿真并制作出倍频效率最高为12%的W波段三倍频器[2]。电子科技大学的研究人员基于国产肖特基二极管,仿真出倍频效率大于4%,相对带宽为27%的宽带平衡三倍频器[3]。还有学者采用变容二极管,设计并仿真出输出频率为140 GHz的二倍频器[4],倍频效率为10.8%。上述几篇文献均采用波导腔体的结构设计,这种结构体积大,不适合体积较小的商用产品,而是适合于航空航天领域。为了能够在体积较小的商品中使用,一般都做成芯片的形式,比如采用(complementary metal oxide semiconductor,CMOS)工艺。美国加利福尼亚大学的研究人员采用45 nm CMOS技术,研制出了一种输出频率135 GHz~160 GHz,倍频效率约为31.7%的有源二倍倍频器[5]。日本东京工业大学的研究人员采用65 nm CMOS技术进行设计并实现了单个晶体管二倍频倍频器[6],并提出了一种优化的缓冲方法,抑制基频分量和其他谐波,同时采用了反馈拓扑结构提高增益。在输入功率为-8 dBm时,基频抑制超过60 dBc,输出频率为100 GHz~123 GHz,饱和输出功率高达5.5 dBm。瑞典查尔姆斯理工大学的研究人员提出了使用分布式超导体-绝缘体-超导体(superconductor-insulator-superconductor,SIS)连接的倍频器[7],导出了描述分布式SIS结作为倍频器特性的解析表达式,对分布式SIS节点的建模表明,采用该方法可以获得较高的转换效率。也有研究人员采用吉尔伯特结构,避免了输出直流偏移,可以提供真正的差分输出信号[8],但是该结构相对复杂,对于分立电路而言需要较多的晶体管,增加成本。以上几种方式是通过有源方式设计倍频器,其倍频效率较高,但是增加了倍频器的复杂性。虽然通过不同工艺可以将倍频器做成小型化,但是这些工艺复杂。为了工艺简单并且达到小型化,本文考虑直接采用制作简单且成本低的印制电路板(printed circuit board, PCB)进行设计。
1 提高倍频器倍频性能的方法
倍频器的原理就是利用非线性器件的非线性效应产生谐波信号,然后通过滤波网络滤除无用谐波并保留有用谐波,最终得到所需的倍频信号。倍频器的系统框图如图1所示,其中低通滤波器是防止所产生的谐波信号反向注入输入端的频率源,避免基波信号发生频率偏移。输入阻抗匹配和输出阻抗匹配是在匹配阻抗,使得所需信号传输效率达到最大。输出滤波网络的作用主要是抑制无用谐波,使得所需谐波通过。

图1 倍频器系统框图Fig.1 The system block diagram of the frequency multiplier
通过对倍频器的研究发现,在设计倍频器时,为提高倍频性能要着重考虑以下几点。
1)选择合适的非线性器件。目前常见的非线性器件有肖特基势垒二极管(schottky barrier diode,SBD)、阶跃恢复二极管(step-recovary diode,SRD)、金属半导体型场效应晶体管(metal-semiconductor field effect transistor,MESFET)、异质结势垒变容二极管(heterostructure barrier varactor,HBV)、高电子迁移率晶体管(high electron mobility transistor,HEMT)等。倍频时所利用的非线性特性主要分为变阻特性和变容特性,当倍频器是利用非线性器件的变阻特性时,倍频带宽较宽,但是倍频效率较低,而当倍频器是利用非线性器件的变容特性时,倍频带宽较窄,但是倍频效率较高。一般变容二极管适合低次倍频(2~4次倍频),而阶跃恢复二极管适合高次倍频,晶体管虽然可以获得倍频增益,但是晶体管受到截至频率的限制,所以其构成的倍频器的使用频段也受到了限制。因此要根据倍频器的设计指标来选择合适的非线性器件。
2)选择适合的非线性器件工作状态。以变容二极管为例,变容二极管倍频器是利用其电容特性进行倍频,在信号的一个周期内,某段时间偏压使PN结进入正向状态,即从反向状态较小的结电容转化到正向状态较大的扩散电容时,其电容变化率很高,从而可以有效体现出其较高的倍频效率,但是当激励过高时,PN结的结电阻所产生的损耗又会降低倍频器的倍频效率。因此对于不同的输入信号功率,需要选择合适的变容二极管偏置电压,使其达到最佳的工作状态。
3)采用合适的电路结构。在设计倍频器时,最常用的电路结构就是平衡结构,即由偶数个二极管组成二极管对,形成串联或并联结构,二极管对可以是同向也可以是反向。一般同向结构可以抑制奇次谐波,反向结构可以抑制偶次谐波,因此这种结构可以抑制部分谐波,而且这种结构可以改善输入阻抗特性。同时二极管数量增加,也会提高倍频信号的输出功率。
4)做好阻抗匹配。在设计高频电路时,阻抗匹配做的好可以使输出功率最大化,因此阻抗匹配无疑是最重要的事情,在设计倍频器时亦是如此。但是有所不同的是,倍频器需要对两个频率信号进行阻抗匹配,即非线性器件的输入电路与输入信号频率进行匹配,输出电路与倍频信号进行匹配。
5)减少不同频率之间的相互干扰。虽然输入信号频率与非线性器件的输出电路阻抗不匹配,但是依然有一定功率的输入信号可以通过,混入输出信号,降低倍频器的性能。倍频信号也是一样,会泄漏到输入端,干扰信号源,从而影响倍频器性能。因此需要在输入电路和输出电路部分增加滤波网络,使得在输入端只有输入信号能够通过,而在输出端,只有所需的倍频信号能够通过。
6)增加空闲电路。一个信号通过非线性器件之后会产生多个谐波,然而有用的谐波只有一个,其他谐波都属于空闲谐波。为了提高有用谐波的效率,就需要这些无用的谐波在电路中没有功率损耗,此时就需要将这些谐波信号接入纯电抗负载,使其功率损耗为零,或者将这些信号反馈回非线性器件,从而再次利用。而构成这些功能的电路就是空闲电路。大多数情况下,空闲电路加在输出滤波网络中。
2 电路设计与仿真
根据Manley-Rowe功率关系[9],变容二极管的倍频效率在理论上可达100%,且所使用的频段较高,需要反向恢复时间较短的二极管,因此在设计无源倍频器时采用GaAs变容二极管MA46H146。在选择基材时,通过权衡价格与损耗等因素,最终选择了介电常数为2.2的RT/duroid 5880。由于微带线过细的情况下,制造工艺很难把控,在相同阻抗情况下基片厚度越厚,线宽越宽,因此选择介质基片厚度为0.508 mm。通过比较不同倍频电路之后,对于非线性器件部分,本文采用如图2所示的反向并联电路结构。反向并联的二极管结构可以抑制偶次谐波,因此可以大大减小输出滤波网络的复杂程度和尺寸,从而减少整个倍频器的尺寸。而且该结构中二极管一端接地,有利于二极管散热,提高倍频器的稳定性。
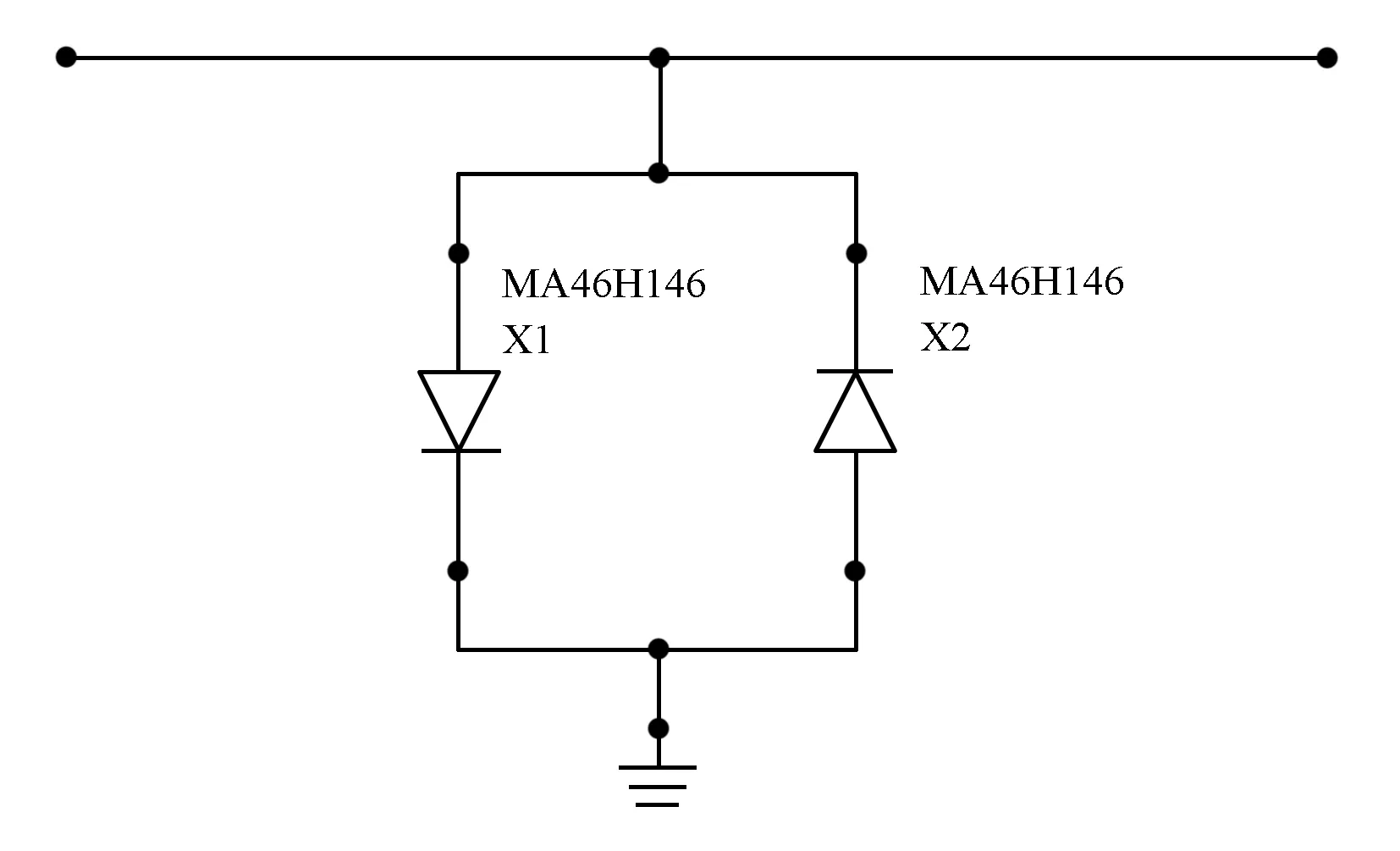
图2 反向并联电路结构Fig.2 Reverse parallel circuit structure
当给一个二极管两端加上电压vd时,流过二极管中PN结的电流可表示为
id=Is(evd/nVT-1)
(1)
式中:Is表示反向饱和电流;n表示发射系数(范围为1~2,与PN结的尺寸、材料和所通过的电流有关);VT表示温度为T时的电压当量。若通过X1二极管的电流为
i1=Is(evd/nVT-1)
(2)
通过X2二极管的电流为
i2=Is(e-vd/nVT-1)
(3)
则二极管对所产生的总电流为
iall=2Issin(vd/nVT)
(4)
当输入信号为正弦信号,即vd=Vcos(ωt),带入上式并进行傅里叶变换后可得
iall=4Is[I1(V/nVT)cos(ωt)+
I3(V/nVT)cos(3ωt)+…]
(5)
由式(5)可知,通过该结构,只会得到奇次谐波,所以该结构通常用于奇次倍频。
方案确定后,利用先进设计系统(advanced design system,ADS)软件对各部分内容进行仿真及优化。首先根据变容二极管MA46H146的数据手册中SPICE参数可知,该二极管的击穿电压为26 V,具有高Q值(大于1.5×104),其中二极管的欧姆电阻取6.5 Ω,封装电容取0.03 pF,寄生电感取0.04 nH。其仿真模型如图3所示。

图3 变容二极管MA46H146等效电路模型Fig.3 The equivalent circuit model of the varactor diode MA46H146
之后通过高低阻滤波器的设计方法,采用巴特沃斯低通原型滤波器对低通滤波器进行设计,在ADS中对所设计的滤波器进行建模,并对尺寸进行优化,然后生成低通滤波器版图,得到如图4所示性能良好的低通滤波器,尺寸约为2.5 mm×2.33 mm。
图4 低通滤波器版图Fig.4 The layout of the low pass filter
该低通滤波器的仿真结果如图5所示。在通带(30 GHz以下)内回波损耗S11小于-20 dB,插入损耗S21大于-1.3 dB,阻带(50 GHz~100 GHz)内插入损耗S21小于-20 dB。由于在该电路中,偶次谐波被抑制,高次谐波能量低,因此无需考虑偶次谐波的信号和高次谐波信号,只需要考虑基波信号和三次谐波信号,对与基波信号20.4 GHz来说可以通过,衰减很低,对于三次谐波信号61.2 GHz来说无法通过,满足所设计倍频器的性能要求。

1—回波损耗S11;2—插入损耗S21。图5 低通滤波器性能仿真图Fig.5 Simulation diagram of low pass filter performance
为便于放置二极管,需要添加一个T字形微带线结构,左边接输入,右边接输出,下边接反向并联的二极管对,二极管对的另一端通过过孔接地。为了得到最佳的输出功率,需要对该结构前后进行阻抗匹配,匹配之前通过搭建电路,读出其基波的输入阻抗为(29.458+j5.98) Ω,同理读出三次谐波的输出阻抗为(33.534-j29.693) Ω,然后通过微带理论将输入阻抗、输出阻抗分别和50 Ω进行阻抗匹配,得到输入匹配电路和输出匹配电路。
由于该电路中偶次谐波被天然抑制,且高次谐波的功率很低,因此只需着重考虑基波抑制。这里采用如图6所示的分支线对其进行抑制,即采用四分之一波长的分支线将基波信号接入纯电抗负载,使其功率损耗为零,形成空闲电路。如果采用带阻滤波器或高通滤波器对基波进行抑制,则需要对滤波器进行设计,其尺寸可能会小一些,但是滤波器设计过程复杂,调试起来也不方便,而且滤波器对有用信号必定是有衰减的。而采用空闲电路的方式对有用信号衰减很小,且调试方便,只需要调整分支线的长度即可。

图6 空闲电路版图Fig.6 The layout of the idle circuit
空闲电路的仿真结果如图7所示,在空闲电路中,基波信号的回波损耗S11为-0.126 dB,而三次谐波信号的回波损耗S11为-28.727 dB,因此空闲电路可以有效抑制基波信号,而对其他谐波信号衰减很低,可以等效带组滤波器或是高通滤波器的效果。该空闲电路是提高基波抑制率的关键。

图7 空闲电路仿真图Fig.7 Simulation diagram of idle circuit
最后将所有电路连接起来进行整体优化,其仿真原理图如图8所示。

图8 无源三倍频器整体仿真原理图Fig.8 Schematic diagram of the whole simulation of passive triplex
优化后生成版图如图9,尺寸约为16.7 mm×4.6 mm。其中二极管的反向并联结构,一端接在图示中的端口,另一端通过过孔接地。

图9 无源三次倍频器版图Fig.9 Passive triple frequency multiplier layout
3 结果分析
在输入频率为20.4 GHz,功率为20 dBm时,谐波平衡仿真结果如图10所示。从图中可以看出,由于采用反向并联结构,所产生的偶次谐波信号功率极低,高次谐波(五次谐波)信号功率也很低,三次谐波输出功率为17.465 dBm,倍频效率为55.78%。
不同频率下三次谐波输出功率如图11所示,从图中可以看出,当输入频率在20.34 GHz~20.45 GHz范围内时,倍频效率大于1%;在20.38 GHz~20.41 GHz范围内时,倍频效率大于10%;在20.4 GHz附近时,倍频效率最高,从图10中可看出具体数值。
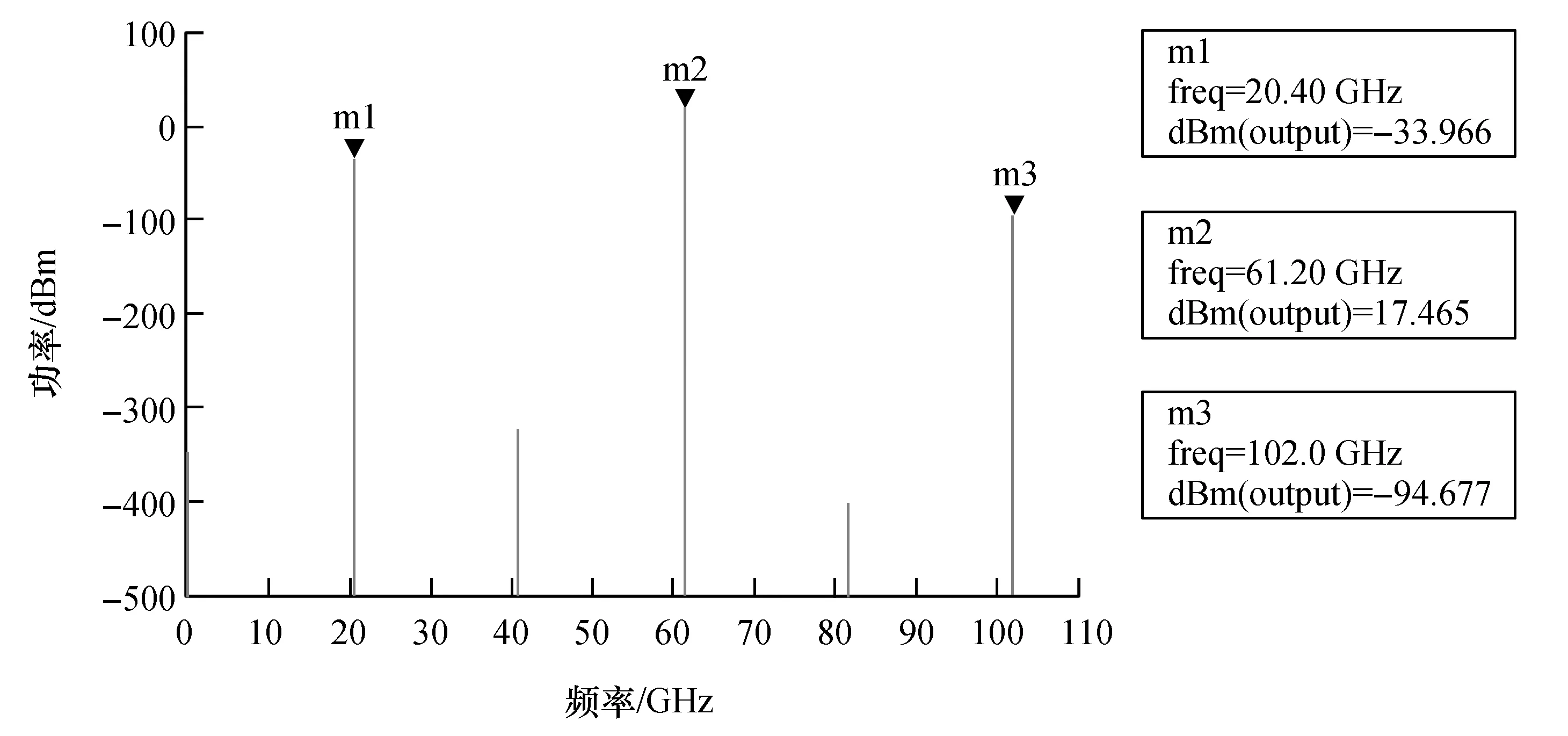
图10 谐波平衡仿真图Fig.10 Harmonic balance simulation diagram

图11 不同频率下的三次谐波输出功率Fig.11 Output power of third harmonic at different frequencies
不同频率下各次谐波输出功率如图12所示,基波抑制大于50 dBc,五次谐波抑制大于110 dBc。

1—三次谐波信号;2—基波信号;3—五次谐波信号。图12 不同频率下各次谐波输出功率Fig.12 Output power of each harmonic at different frequencies
从该结果中可以看出,所设计的倍频器倍频效率较高,无用谐波抑制效果很好,只是倍频带宽偏窄,这是由于采用变容二极管导致的。由于该倍频器设计初衷是用于ISM(industrial scientific medical)频段中的61 GHz~61.5 GHz内,因此该结果满足需求。由于该倍频器频率较高,因此部分结构的尺寸要求比较严格,通过仿真研究可知,当尺寸存在微小误差时,倍频带宽变化不大,主要是倍频频带发生偏移,因此要求误差小于0.1 mm,否则会导致倍频频段偏离设计频段。
4 结 论
通过对毫米波倍频器的研究,本文设计出一种应用于ISM频段中中心频率为61.25 GHz的毫米波倍频器,该倍频器的最高倍频效率大于50%,但是倍频带宽偏窄,只适用于窄带系统。后续需要对所设计倍频器进行实物制作,进一步进行验证。

