三向网格混凝土锥面密肋网壳的静力性能分析

杨水艳，张华刚*，2，马克俭，2

(1.贵州大学 空间结构研究中心，贵州 贵阳 550025；2.贵州省结构工程重点实验室，贵州 贵阳 550025)

我国从上世纪50年代便开始了混凝土薄壳结构的应用[1]，后由于混凝土曲面施工的困难及现代大跨度空间结构的兴起，致使薄壳结构逐渐淡出了工程视野[2-3]。但混凝土材料具有良好的抗压、耐久和防火性能，因此，众多学者对混凝土壳体结构的创新研究工作并未停止，其中组合壳体结构[4-5]和V形折板结构[6]是两个重要的研究方向。张华刚[7-11]等采用密肋平板交汇并提出了一类混凝土折板形密肋网壳结构。这些工作推动了混凝土空间结构的发展。

相比于旋转面薄壳结构，由平板交汇的折板结构施工简便，构造简单，且几乎没有声学问题，但结构刚度相对较差，荷载较大时往往需要增加折梁来进一步明确传力途径[12]。对其中的伞状结构，由折缝形成的汇交折线拱是主要传力结构，承担了较大的内力。因此，刘开国[13]等在1985年提出了V形折板式伞状结构，并进行了12 m跨结构的工程实践。可见，对组成伞状结构的三角形平板起折，是提高结构刚度和承载力的一种有效措施，但相应也增大了折缝的施工处理难度。事实上，当结构跨度较大时，对三角形平板加肋将是提高结构面外刚度的另一种有效措施，由此可获得伞状结构的另一种形状——锥面密肋网壳结构[7]。

为了了解锥面密肋网壳在点支承条件下的静力性能，本文采用数值模拟方法来分析结构的挠度和内力分布，并考虑构件刚度的影响进行参数化分析，以期确定主要构件尺寸的合理选值范围，为工程应用提供参考。

1 结构形式及算例基本情况

1.1 结构形式

锥面网壳结构形式如图1(a)所示。主结构由脊线和边梁构成，脊线与边梁交汇处设置支座，密肋梁采用三向网格布置。沿斜面等标高处形成封闭圈的密肋梁称为环向肋，剩余的密肋梁称为拱向肋。

1.2 算例情况

基本算例的剖面如图1(b)所示。跨度L为30 m,矢高f为7.5 m。密肋平板的网格构造如图1(c)所示。网格水平投影长度均为1.5 m。构件尺寸如图1(d)所示。材料采用C40混凝土，弹性模量Ec=3.25×107kN/m2，泊松比v=0.2，钢筋混凝土密度为2.42×103kg/m3。1/6结构平面如图1(e)所示。图1(e)中，编号BL、JX和ML分别代表边梁、脊线和密肋梁，1～10为节间的编号。不计自重的计算荷载为5.0 kN/m2，脊线和边梁交汇处节点应约束全部自由度。结果分析时，用Wmax表示结构最大挠度，Fn表示轴力，M表示弯矩。结构内力符号规定如下：Fn以受拉为正；M以使梁的上部纤维受拉为负；弯矩分别以左和右确定其截面位置，左右方向与图1(e)中节间编号顺序方向一致。

图1 基本算例结构Fig.1 Basic example structure

参数化分析是在基本算例的基础上，通过调整单因素来确定。

2 结构静力分析

2.1 结构挠度

基本算例的挠度分布如图2所示。由于脊线形成的折线拱的刚度强于边梁，致使密肋板的变形主要发生在靠近边梁的区域，但最大挠度仅为9.55 mm，约为结构跨度的1/3 142，表明结构具有较强的整体刚度，且脊线是密肋平板的有效弹性支承。

图2 结构挠度Fig.2 Structural deflection

2.2 结构内力

结构轴力和弯矩分布如图3和图4所示，部分构件内力的数值结果如图5和图6所示。脊线主要受压，但靠近支座处的弯矩数值较大。边梁的轴力和弯矩数值几乎处于同一量级。可见，脊线与支座附近的梁段和全跨边梁应按偏心受力构件来计算承载力。密肋平板上，梁的弯矩分布规律与用作楼盖时类似，但弯矩数值较小。数值较大的轴力主要出现在密肋板中部区域的环向肋梁上，可见密肋梁不应按纯受弯构件计算其承载力，梁上通长纵筋的配置应能抵抗偏心轴力的影响。

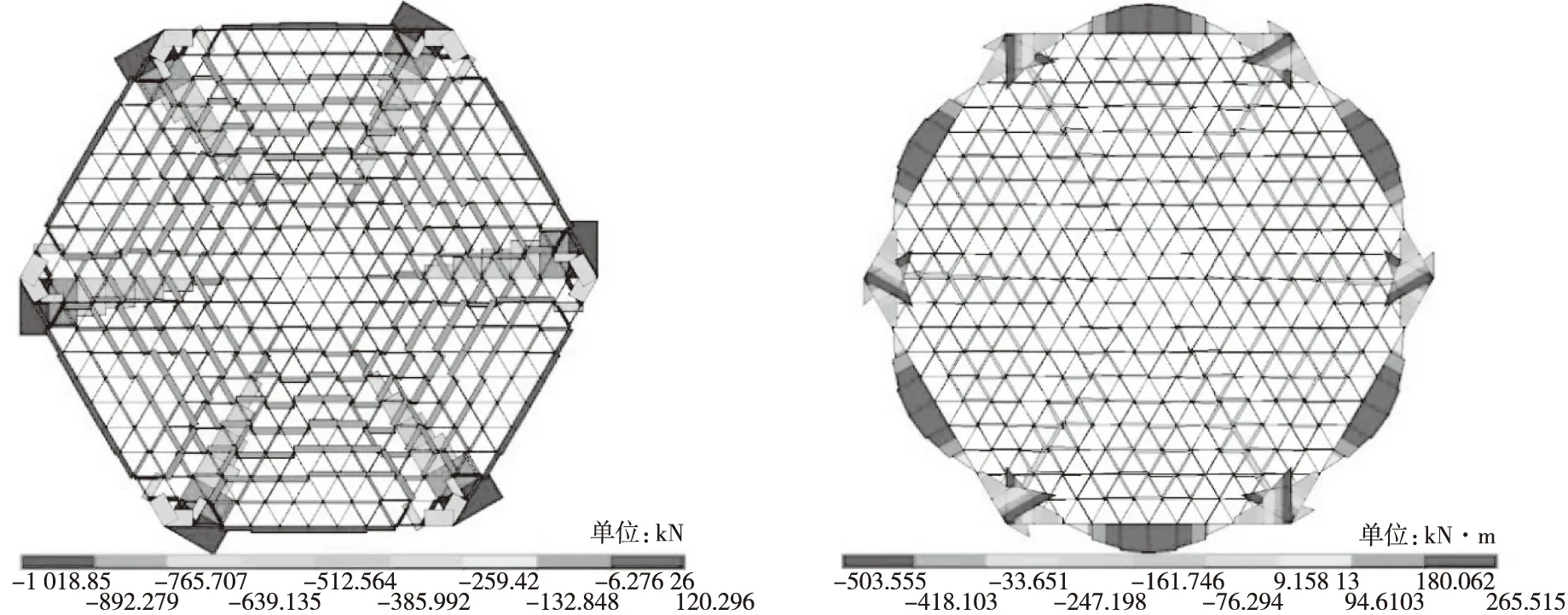
图3 结构轴力图 图4 结构弯矩图Fig.3 Axial force diagram of structure Fig.4 Bending moment diagram of structure

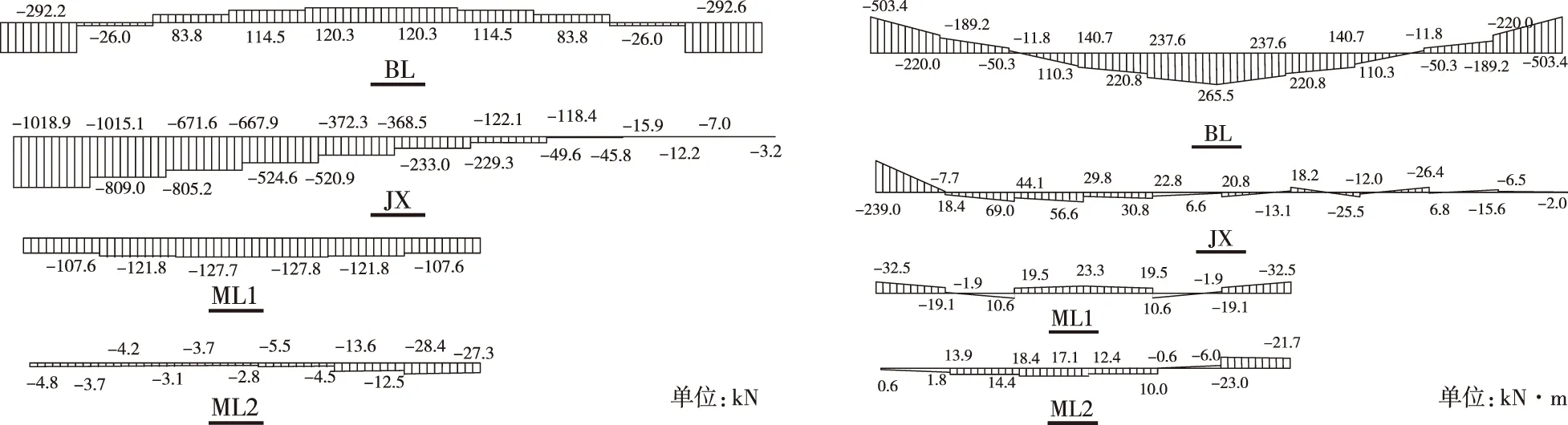
图5 部分构件轴力图 图6 部分构件弯矩图 Fig.5 Axial force diagram of partial members Fig.6 Bending moment diagram of partial members

3 静力性能的参数化分析

3.1 矢跨比对结构静力性能的影响

基于图1所示结构，分别考虑矢跨比、边梁刚度、脊线刚度、密肋梁刚度和屋面板厚对结构静力性能的影响，修改相应的参数做静力计算，各参数取值情况如下：

(1)矢跨比分别取1/8、1/7、1/6、1/5、1/4和1/3这6个算例进行数值模拟分析。

(2)考虑边梁刚度对结构静力性能影响时，脊线截面高度取650 mm，边梁截面高度的取值分别为700、750、800、850、900、950 mm。

(3)考虑脊线刚度对结构静力性能影响时，边梁截面高度取950 mm，脊线截面高度的取值分别为600、650、700、750、800、850 mm。

(4)考虑密肋梁刚度对结构静力性能影响时，密肋梁截面高度的取值分别为300、350、400、450、500、550 mm。

(5)考虑屋面板厚对结构静力性能的影响时，屋面板厚的取值分别为50、60、70、80、90、100 mm。

3.2 矢跨比对结构静力性能的影响

矢跨比的改变对Wmax的影响如图7所示。由图7可以看出：当矢跨比为1/8时，Wmax为11.57 mm；当矢跨比为1/4时，Wmax为9.55 mm,降低了17.5%；继续增大矢跨比，最大挠度又呈增长趋势。

图8和图9给出不同矢跨比对结构部分构件内力的影响结果，节间位置如图1(e)所示。矢跨比对BL和ML的弯矩影响较小，对JX的内力和BL、ML的轴力影响均较大，且内力数值随着矢跨比的增大均呈下降趋势。矢跨比为1/8和1/3相比，由图8和图9可以看出： BL/1#左和BL/5#右的轴力数值分别降低了55.8%和62.2%，ML1/3#左和ML1/5#右的轴力数值分别降低了44.3%和44.4%，JX/1#左的轴力数值和弯矩数值分别降低了28.0%和55.6%。

上述计算结果表明，虽然增大矢跨比有利于降低结构内力，但是矢跨比大于或等于1/3后，密肋平板的实际边长将发生突变，且当网格数一定时，将显著降低结构刚度并增加自重。因此结构矢跨比不宜大于1/4。

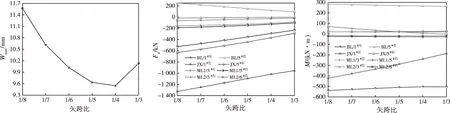
图7 矢跨比对Wmax的影响 图8 矢跨比对Fn的影响 图9 矢跨比对M的影响Fig.7 Effect of rise-span ratio on Wmax Fig.8 Effect of rise-span ratio on Fn Fig.9 Effect of rise-span ratio on M

3.3 边梁刚度对结构静力性能的影响

边梁刚度的改变对结构最大挠度的影响如图10所示。由图10可以看出，Wmax随着边梁刚度的增大而显著下降。边梁截面高度为750 mm和950 mm相比，Wmax分别为10.7 mm和8.4 mm，降低了21.5%，可见边梁刚度的增大对Wmax的影响较大。

改变边梁刚度对内力的影响如图11和图12所示。由图11和图12可以看出：边梁截面高度从700 mm增加到950 mm, BL/1#左和BL/5#右的弯矩数值分别增加了38.6%和34.2%，JX/1#左的弯矩数值降低了15.9%；JX/5#右的弯矩数值始终为个位数，密肋梁的内力未见明显增长。

基本算例的分析结果已表明，结构的变形和内力主要集中在三角形密肋平板的重心附近，荷载主要由脊线向支座传递。因此，提高边梁刚度可增强密肋平板的边界约束效应来降低其挠度，但不会改变结构的传力途径，也就不会明显影响脊线和密肋梁的内力分布。边梁在满足承载力要求前提下可采用较小的高跨比。

图10 边梁刚度对Wmax的影响 图11 边梁刚度对Fn的影响 图12 边梁刚度对M的影响Fig.10 Effect of side beam stiffness Fig.11 Effect of side beam stiffness Fig.12 Effect of side beam stiffness on Wmax on Fn on M

3.4 脊线刚度对结构静力性能的影响

改变脊线刚度对Wmax的影响如图13所示。由图13可以看出，Wmax与脊线刚度呈线性变化。当脊线截面高度从600 mm增到850 mm时，Wmax分别为8.8 mm和8.6 mm ，降低了2.3%。因此，脊线刚度的增大对延缓结构变形效果不明显，变形主要发生在密肋平板上。

改变脊线刚度对结构部分构件内力的影响如图14和图15所示。由图14和图15可以看出：随着脊线刚度的增大，除了增大自身内力外，BL和ML2的内力均呈减小趋势。如脊线截面高度为600 mm和850 mm相比，BL和ML2的内力数值的变化率均小于10%，JX/1#左和JX/5#右的轴力数值分别增加了14.9%和31.7%，弯矩数值分别增加了101.7%和366.7%。

脊线成拱后自身变形较小。因此，脊线刚度的增大对提高结构整体刚度效果欠佳，且过大的脊线刚度会使自身内力大幅度增加，建议脊线截面高度的取值满足强度设计要求即可。

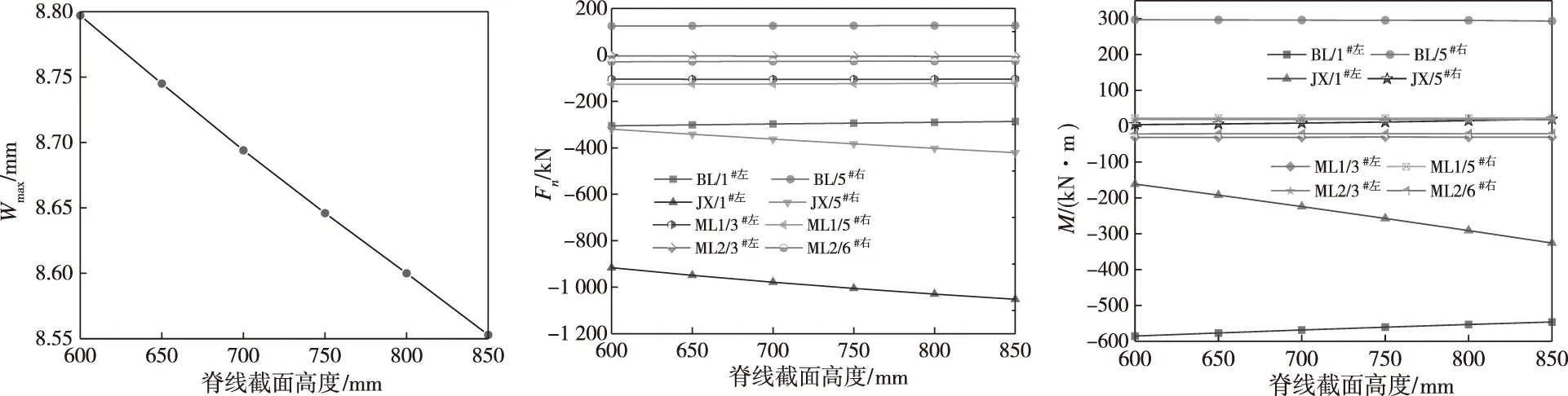
图13 脊线刚度对Wmax的影响 图14 脊线刚度对Fn的影响 图15 脊线刚度对M的影响Fig.13 Effect of ridge beam stiffness Fig.14 Effect of ridge beam stiffness Fig.15 Effect of ridge beam stiffness on Wmax on Fn on M

3.5 密肋梁刚度对结构静力性能的影响

改变密肋梁刚度对Wmax的影响如图16所示。由图16可以看出，密肋梁刚度的增大可有效地降低结构变形。密肋梁截面高度为300 mm和550 mm相比，Wmax分别为13.1 mm和7.0 mm，降低了46.6%。

密肋梁刚度对结构部分构件内力的影响如图17和图18所示。由图17和图18可以看出：随着密肋梁刚度的增大，除了BL的弯矩数值略有下降趋势外，剩余构件的内力数值均呈上升趋势。密肋梁截面高度为300 mm和550 mm相比，BL/1#左和JX/1#左的轴力数值提高率均在20%以上；ML1/3#左、ML1/5#右和ML2/6#右的内力数值提高率均在75%以上。

上述分析表明：虽然增大密肋梁刚度可显著提高结构整体刚度，但结构变形数值本身较小，工程应用时结构破坏更多地会受强度控制，刚度过大的密肋梁还会增加结构自重。因此，建议密肋梁的截面高度可采用结构跨度的1/100～1/75。

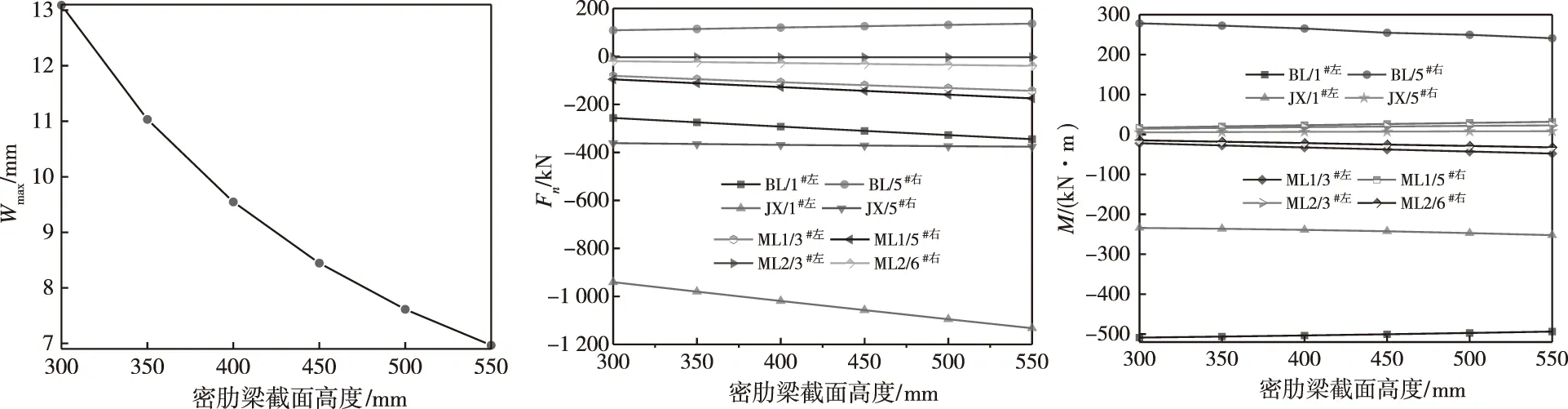
图16 密肋梁刚度对Wmax的影响 图17 密肋梁刚度对Fn的影响 图18 密肋梁刚度对M的影响Fig.16 Effect of multi-ribbed beam Fig.17 Effect of multi-ribbed beam Fig.18 Effect of multi-ribbed beam stiffness on Wmax stiffness on Fn stiffness on M

3.6 屋面板厚对结构静力性能的影响

改变屋面板厚对Wmax的影响如图19所示。由图19可以看出，Wmax随屋面板厚的增大而减小，屋面板厚的改变对Wmax的影响较小。当屋面板厚从50 mm增加到100 mm时，Wmax分别为9.55 mm和9.38 mm，减小了1.8%。

屋面板厚的改变对结构部分构件内力的影响如图20和图21所示。由图20和图21可以看出：屋面板厚的增大除了增大BL构件的内力数值外，其他构件内力均呈下降趋势；且屋面板厚的增大对JX/5#的内力和ML的轴力数值影响较大。如屋面板厚为50 mm和100 mm相比，BL/1#左和BL/5#右的轴力数值分别增加了10.3%和0.6%，弯矩数值分别增加了2.0%和4.5%；ML1/3#左和ML1/5#右的轴力数值分别降低了25.2%和23.5%。

综合上述分析可得，加大屋面板厚对提高结构整体刚度贡献较小，对调整结构内力影响有限，不建议采用过厚的屋面板。

图19 屋面板厚对Wmax的影响 图20 屋面板厚对Fn的影响 图21 屋面板厚对M的影响 Fig.19 Effect of roof slab stiffness Fig.20 Effect of roof slab stiffness Fig.21 Effect of roof slab stiffness on Wmax on Fn on M

4 结论

通过对锥面密肋式网壳在竖向荷载作用下进行有限元模拟分析，得到以下结论：

(1)结构最大挠度发生在密肋平板重心位置，致使脊线成为主要传力结构。结构同时存在轴力和弯曲内力，因此承载力设计应考虑偏心轴力的影响。

(2)矢跨比的改变将影响密肋平板沿结构跨度方向的实际边长，从而会降低结构刚度并增加自重，结构矢跨比不宜大于1/4。

(3)边梁刚度的提高可加强对拱向肋的约束，但不会根本改变结构的传力途径，因此边梁可采用较小的高跨比。

(4)脊线作为密肋平板的弹性支承，脊线成拱后的刚度较大，因此，进一步加强脊线刚度对提高结构受力性质意义不大。

(5)密肋梁刚度的提高对自身内力影响较大。密肋梁截面高度宜按结构跨度的1/100～1/75确定。

(6)屋面板厚的改变对提高结构整体刚度的贡献较小，对内力影响有限。屋面板厚的选取满足构造要求即可。