基于黏滞阻尼器的单跨悬索桥地震位移响应控制

卢长炯 卢明奇

摘 要：工程中，黏滞阻尼器常用于降低大跨度单跨悬索桥的顺桥向地震位移响应。为此，有必要深入研究其主要技术参数对桥梁结构地震位移响应的影响作用规律。以主跨1 250 m单跨悬索公路桥为例，建立其三维有限元数值分析模型，选取七条实测地震记录，通过时程分析法进行计算，得到结构重点部位的地震位移响应。研究表明：随着阻尼系数的增大，大跨度单跨悬索桥主梁左、右两端的顺桥向地震位移呈减小趋势;当阻尼系数较大时，继续增大阻尼系数或者改变速度指数，主梁左、右端最大地震位移响应值变化不显著;黏滞阻尼器对索塔顶部的地震位移响应无明显影响;阻尼系数增加，单跨悬索桥左、右两侧索塔横梁的最大地震位移值先减小后增大;当阻尼系数较大时，速度指数增加，该处的最大地震位移值减小。

关键词：悬索桥;黏滞阻尼器;地震响应;有限元;位移

中图分类号：U442.5+5  文献标志码：A

单跨悬索桥采用桥墩支撑边跨，提高了梁体结构的经济性，常用于高山峡谷地区或者道路接线受限等情况，是悬索桥结构体系的重要形式之一，在交通工程中得以越来越广泛的应用。由结构的动力特性可知，单跨悬索桥属于长周期、柔性结构，在地震作用下其上部梁体和索塔易于产生较大的位移响应，进而可能造成严重的结构损伤和破坏。如何有效地控制其结构地震位移是这类桥型抗震设计必须解决的关键问题。目前，国内外相关的研究工作主要有：VADER等[1]研究了阻尼器对悬索桥桥塔地震响应的影响作用;焦常科等[2]分析了弹性拉索、黏滞阻尼器及二者组合使用对大跨度三塔悬索桥的减震控制效果，发现该类减震措施能够有效控制塔梁相对位移，但会显著增大中塔底部的内力响应;伍隋文等[3]提出了黏滞阻尼器可以有效地控制梁端纵向位移，且当阻尼指数不变时，主梁纵向位移随着阻尼系数的增大不断减小，但减幅不大;张玉平等[4]探讨了弹塑性软钢阻尼器对大跨度三塔悬索桥的减震控制效果，研究表明：设置软钢阻尼器可有效减小塔梁相对位移;郭志明等[5]对设柔性中央扣的特大跨度悬索桥纵向抗震体系进行了计算分析，研究认为黏滞阻尼器的减震效果远好于柔性中央扣;李奇[6]以某实际工程为例，探讨了大跨度悬索桥的抗震、抗風标准及应采用的减震、抗风措施。但是，现有研究的分析对象多为两跨、三跨或者多跨悬索桥体系，针对大跨度单跨悬索桥上部梁体和索塔地震位移响应减震控制的研究还相对较少，以往的研究结论是否适用于单跨悬索桥仍需深入考察。为此，本文基于某实际工程的单跨悬索桥设计方案，研究了黏滞阻尼器主要技术参数对大跨度单跨悬索桥地震位移响应的影响规律。

1 有限元分析模型

1.1 工程概况

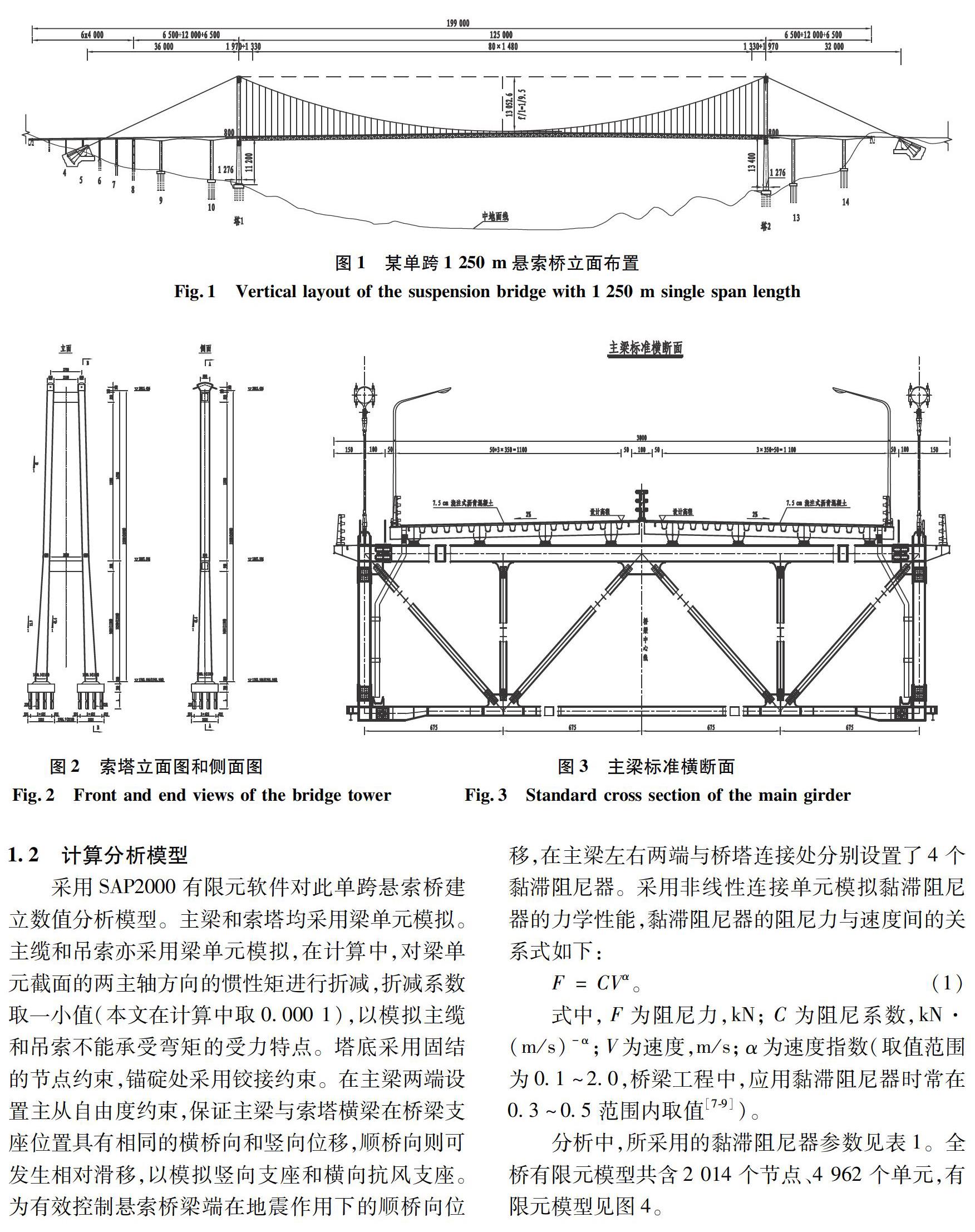
某单跨悬索公路桥，抗震设防烈度为八度，二类场地，主跨1 250 m，其桥型立面布置见图1。桥梁主跨矢跨比为1∶9.5，索塔采用双横梁刚构式混凝土索塔，一侧索塔塔高252.88 m，另一侧索塔塔高269.88 m，均设上下两道横梁，塔柱采用带圆倒角的矩形截面，塔柱立面如图2所示。主梁采用钢桁梁，上下桁架中心间距取7.8 m。钢桁梁钢材采用Q345qD。主梁断面如图3所示。主梁在两个桥塔处均设置横向抗风支座、竖向拉压支座。主缆采用预制束股法（pretormed parallel wire standards，PPWS）架设，高强镀锌钢丝采用φ5 mm系列，索股钢丝根数为91丝，抗拉强度为1 770 MPa，锚固于重力式锚碇上。吊索采用平行钢丝吊索，抗拉强度为1 770 MPa。主梁与索塔横梁间沿顺桥向布置黏滞阻尼器，以降低地震作用下桥梁的纵向位移。

1.2 计算分析模型

采用SAP2000有限元软件对此单跨悬索桥建立数值分析模型。主梁和索塔均采用梁单元模拟。主缆和吊索亦采用梁单元模拟，在计算中，对梁单元截面的两主轴方向的惯性矩进行折减，折减系数取一小值（本文在计算中取0.000 1），以模拟主缆和吊索不能承受弯矩的受力特点。塔底采用固结的节点约束，锚碇处采用铰接约束。在主梁两端设置主从自由度约束，保证主梁与索塔横梁在桥梁支座位置具有相同的横桥向和竖向位移，顺桥向则可发生相对滑移，以模拟竖向支座和横向抗风支座。为有效控制悬索桥梁端在地震作用下的顺桥向位移，在主梁左右两端与桥塔连接处分别设置了4个黏滞阻尼器。采用非线性连接单元模拟黏滞阻尼器的力学性能，黏滞阻尼器的阻尼力与速度间的关系式如下：

2 地震记录的选择

从美国太平洋地震工程研究中心地震记录数据库中选取与我国二类场地条件相对应的7条地震记录，见表2。将七条地震记录的加速度反应谱平均值与规范设计谱[10]进行比较，如图5所示，加速度反应谱平均值和规范谱偏差均在20%以内，满足文献[11]对地震记录选取的要求。

3 黏滞阻尼器对大跨度单跨悬索桥地震位移响应的影响规律  通过地震响应时程分析，可得黏滞阻尼器主要技术参数C、α对单跨悬索桥顺桥向最大地震位移响应的影响作用曲线，如图6所示。由图6可见，随着阻尼系数C的增大，主梁左、右两端的顺桥向位移均呈减小趋势，当阻尼系数C≥15 000 kN（m/s）-α，此时，继续增大阻尼系数C或者改变速度指数α，主梁左、右端最大位移响应值均无明显变化，这说明黏滞阻尼器对单跨悬索桥主梁顺桥向位移的减震控制能力已经得到了最大程度的发挥。由图6还可以看出，主梁左、右端最大位移响应值随着速度指数α的增加变化较小，这是因为大跨度单跨悬索桥属于长周期结构，对应于质量参与系数和振型影响系数较大的振动周期较多地处于结构地震反应谱的位移敏感区范围内[12]，其速度响应量值并非十分显著，而速度指数α的减震作用则是对周期处于速度影响区内的振型影响明显，因此，图6中主梁左右端最大位移响应值随着速度指数α的增加并未出现较明显的变化。

图7为黏滞阻尼器速度指数α分别为0.3、0.4、0.5时，悬索桥左、右两侧索塔顶部最大地震位移响应值与阻尼系数C的关系曲线，可见阻尼系数C和速度指数α的变化对索塔顶端的位移影响不大，这表明：主梁两端布置的黏滞阻尼器对索塔顶部的地震位移响应无明显作用。

图8为黏滞阻尼器速度指数α分别为0.3、0.4、0.5时，悬索桥左、右两侧索塔横梁（与主梁相连处）最大地震位移值随着阻尼系数C的变化曲线。由图8可见，随着阻尼系数C的增加，悬索桥左、右两侧索塔横梁的最大地震位移值先减小后增大;当C≥3 750 kN（m/s）-α时，随着速度指数α的增加，悬索桥左、右两侧索塔横梁的最大地震位移值减小。

4 结论

本文对某大跨度单跨悬索桥建立三维有限元分析模型，通过时程分析方法研究了黏滞阻尼器的阻尼系数C、速度指数α对桥梁地震位移响应的影响规律，得出以下结论：

（1）大跨度单跨悬索桥主梁左、右两端的顺桥向地震位移随着阻尼系数的增大，呈减小趋势，当阻尼系数较大时，继续增大阻尼系数或者改变速度指数，主梁左、右端最大地震位移响应值变化不显著。

（2）单跨悬索桥主梁两端布置的黏滞阻尼器对索塔顶部的地震位移响应无明显作用。

（3）随着阻尼系数的增加，单跨悬索桥左、右两侧索塔横梁的最大地震位移值先减小后增大。当阻尼系数较大时，随着速度指数的增加，索塔横梁的最大地震位移值减小。参考文献：

[1] VADER T S，MCDANNIEL C C.Influence of dampers on seismic response of cable-supported bridge towers[J].Journal of Bridge Engineering，2007，12（3）： 373-379.

[2] 焦常科，李愛群，王浩.三塔悬索桥地震响应控制[J].振动、测试与诊断，2011，31（2）： 156-161.

[3] 伍隋文，李建中.单塔地锚式悬索桥减震阻尼器参数分析[J].振动与冲击，2013，35（S1）：9-12，16.

[4] 张玉平，王浩，邹仲钦，等.大跨度三塔悬索桥弹塑性软钢阻尼器减震控制[J].振动与冲击，2018，37（23）：226-223.

[5] 郭志明，汪鸿鑫，叶爱君.设柔性中央扣的特大跨度悬索桥纵向抗震体系研究[J].桥梁建设，2019，50（1）：38- 43.

[6] 李奇.某大跨度悬索桥抗震、抗风技术研究[J].交通科技，2019（2）：13-15.

[7] 亓路宽，宋宇亮，王君杰，等.自锚式悬索桥动力特性及减震效果[J].北京工业大学学报，2008，34（9）： 950-954.

[8] 丁礼华，段平，董熙，等.黏滞阻尼器对自锚式悬索桥的减震控制分析[J].施工技术，2017，46（24）： 117-120.

[9] 郑锋利，陈逸民，李建中，等.塔梁连接方式对多塔悬索桥地震反应的影响[J].公路交通科技，2020，37（8）： 58-65.

[10]中华人民共和国交通运输部.公路桥梁抗震设计规范：JTG/T 2231—01—2020[S]. 北京：人民交通出版社，2020.

[11]中华人民共和国住房和城乡建设部.建筑抗震设计规范：GB 50011—2001[S]. 北京：中国建筑工业出版社，2010.

[12]CHOPRA A K. Dynamics of structures： theory and applications to earthquake engineering[M]. Upper Saddle River： N.J. Prentice Hall，2012.

（责任编辑：于慧梅）

Abstract： Viscous dampers are commonly used to reduce the seismic displacement responses along the longitudinal direction of long span suspension bridges in engineering projects. Therefore， it is necessary to study the seismic displacement responses of bridge structures affected by main technical parameters of viscous dampers. Taking the single-span suspension bridge with the main span of 1 250 m as an example， its three-dimensional finite element numerical analysis model was established. Seven measured seismic records were selected and the seismic displacement responses of key parts of the bridge structure were obtained by the time-history analysis method. According to the results， the longitudinal seismic displacements at the left and right ends of the main girder of the single-span suspension bridge decrease with the increase of damping coefficient. However， when the damping coefficient is large enough， further increase in the damping coefficient itself or altering the velocity index do not lead to dramatic changes in the maximum seismic displacement responses of both ends of the main girder. Viscous dampers have no obvious effects on the seismic displacement of the top of the bridge towers. With the increase of damping coefficient， the maximum seismic displacement of transverse girders of the left and right sides of bridge tower will decrease first and then increase. As for larger damping coefficient， the maximum seismic displacement at the same places will decrease with the increase of velocity index.

Key words： suspension bridge; viscous damper; seismic responses; finite element; displacement