非奇异H-矩阵的一组判定条件*

魏盈盈，罗 彪，莫宏敏

(吉首大学数学与统计学院，湖南 吉首 416000)

1 基础知识

设Cn×n表示n×n阶复矩阵的集合.对于A=(aij)∈Cn×n,N+={1,…,n},α∈(0,1],记

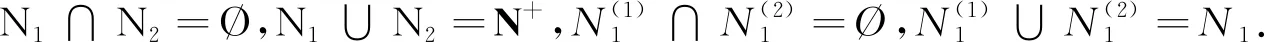
定义1[1]设A=(aij)∈Cn×n.若对于∀i∈N+,有|aii|>Ri,则称A为严格对角占优矩阵,记A∈D;若存在正对角矩阵X,使得AX∈D,则称A为广义严格对角占优矩阵(也称A为非奇异H-矩阵),记A∈D*.

引理1[2]设A∈Cn×n,若存在正对角矩阵X,使得AX∈D*,则A∈D*.

引理2[3]设A∈Cn×n且A为α-链对角占优矩阵,α∈(0,1],若A满足下列条件之一:

(1)A为严格α-链对角占优矩阵;

则A为非奇异H-矩阵,即A∈D*.

引理3[4]设σ,γ为任意的2个非负实数,α∈[0,1],则有αγ+(1-α)σ≥γασ1-α.

2 主要结果及其证明

引入如下符号：

(1)

因此0<βi≤r<1(i∈N2).

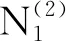
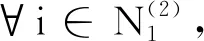
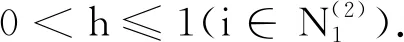
由(1)式可得

取充分小的正数ε,使其满足

(2)

构造正对角矩阵D=diag(d1,d2,…,dn),记B=AD=(bij),其中

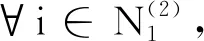
又由σi的表达式可知

(3)

因此

(ⅲ)对于∀i∈N2,由βi的表达式可得

因此，公共英语课教师可根据学生所在院系和近期所学医学课程，进行针对性备课，给予更多课外知识补充，为今后专业英语教学打下基础。而对于公共英语课内容，可变换多种教学和考核形式，鼓励并教会学生自学其中较简单的内容，在课堂上讨论学生不懂的问题，学生之间也可相互解答，教师阶段性地给予总结，表扬提问积极的学生，激发其对英语的内在兴趣。此外，根据学生要求开设基础英语兴趣班、日常英语兴趣班等，充分利用校内优秀留学生资源，互帮互助，亦可形成良性循环。

因此

(4)

且(4)式至少有1个严格的不等式成立,则A∈D*.

证明构造正对角矩阵D=diag(d1,d2,…,dn),记B=AD=(bij),其中

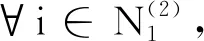
(ⅲ)对于∀i∈N2,0<βi≤r<1,由βi的表达式可得

类似于定理2的证明,利用引理1和引理2可得如下结论：

3 数值算例

例1 设

|a11|=6.1<α(|a12|+|a13|δ3+|a14|+|a15|δ5)+(1-α)S1=6.4,

|a22|=6<α(|a21|+|a23|δ3+|a24|+|a25|δ5)+(1-α)S2=6.2,

|a44|=3.8>α(|a41|+|a42|δ3+|a43|+|a45|δ5)+(1-α)S4=3.7.

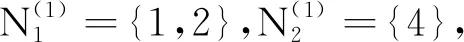
所以此算例不满足文献[5]中定理1的条件.

(ⅱ)对于本研究,N1={1,2,4},N2={3,5},求得r=0.8,β3=0.24,β5=0.768,此时

所以此算例满足定理1的条件,即A为非奇异H-矩阵.

例2设

|a33|=4<α(|a31|δ1+|a32|δ2+|a34|+|a35|)+(1-α)S3=5.25,

|a44|=3<α(|a41|δ1+|a42|δ2+|a43|+|a45|)+(1-α)S4=3.125,

|a55|=4.7>α(|a51|δ1+|a52|δ2+|a53|+|a54|)+(1-α)S5=4.575.

所以此算例不满足文献[5]中定理1的条件.

(ⅱ)对于本研究,N1={3,4,5},N2={1,2},求得r=0.56,β1=0.56,β2=0.329 6,此时

所以此算例满足定理1的条件,即A为非奇异H-矩阵.