含沙固液两相流动对变径管道冲蚀磨损影响
*段文博 马帅 王洁 万永刚 张立平
(1.齐齐哈尔医学院医学技术学院物理教研室 黑龙江 161000 2.中国电力工程顾问集团公司东北电力设计院有限公司 吉林 130000)
引言
出于减小管道冲蚀磨损及提高部件使用寿命的目的,众多国内外学者对管道的冲蚀现象进行了研究,并总结出了大量的冲蚀磨损理论与数学模型。
Zhang等采用数值计算方法分析了管道的冲蚀情况,结果表明数值计算方法与实验方法分析出的冲蚀情况吻合度较好,可以采用数值计算模拟管道的冲蚀磨损。
王凯等对含有沙粒的液固两相流、等直径弯管进行了分析,研究了管道中不同位置的冲蚀磨损率。
刘寒秋等利用数值模拟方法研究了海洋工程作业中的冰水混合物对直角弯管的磨损,并给出了减小管道冲蚀磨损的相关建议。
孙强等利用CFD的动网格技术,研究了不同振动工况下水平及竖直圆管转角处的冲蚀磨损特性,并预测了管道寿命变化情况。
可以看到,在管道的冲蚀磨损研究领域研究方向主要集中在等直径管道方面,而对于变直径管道的冲蚀磨损研究相对较少。鉴于此,本文以变径管作为研究对象,以常见的沙粒与水分别作为固相及液相,同时加入重力的影响,分析液相速度及沙粒粒径对变径管道的冲蚀磨损影响规律,以期为变径管道的设计、防护及结构优化提供一定的参考。
1.冲蚀磨损方程
固体颗粒对管道的冲蚀磨损,可利用离散相(DPM)冲蚀磨损方程进行计算。冲蚀磨损方程如式(1)所示:
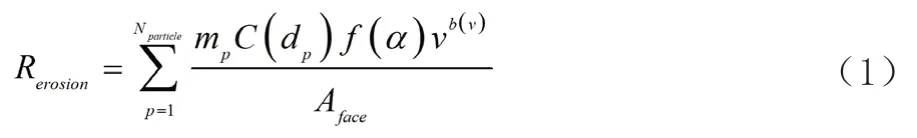
式中,Rerosion表示颗粒冲击管道壁面的磨损速率,kg/(m2·s);NParticle为离散相碰撞数目;mp为离散相的质量流量,kg/s;C(dp)为颗粒的粒径函数,取为1.8×10-9;v为固体颗粒的相对速度,m/s;b(v)为颗粒的相对速度函数,取为2.6;Aface为壁面面积,m2;f(a)为侵入角函数。
2.几何模型与计算条件
本文变径管道的几何模型如图1所示,分为上游段A,变径段B及下游段C。网格划分采用O型网格。以面射流的方式在管道入口释放固体颗粒。选择密度为1000kg/m3的液态水为连续相,密度为1500kg/m3的沙粒为离散相。采用SIMPLE算法对压力速度进行耦合求解,初始化流场,开始计算。
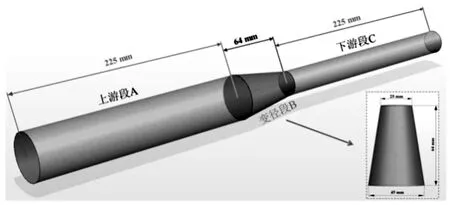
图1 变径管道几何模型
3.结果与讨论
(1)颗粒直径对管道冲蚀磨损的影响
经计算得出,随着颗粒尺寸的增大,管道的冲蚀磨损率也在不断增大。因大尺寸的固体沙粒质量较大,受到的惯性力也较强,所以大尺寸颗粒将具有更大的动能,当颗粒与管道发生摩擦撞击时,具有更大动能的大尺寸固体颗粒对管道壁面的破坏程度将会比小尺寸颗粒严重的多,这就造成了管道的冲蚀率随着颗粒直径增大而增大。

图2 不同颗粒尺寸管道壁面的冲蚀磨损云图
图2为两种不同颗粒尺寸条件下管道壁面的冲蚀磨损云图。从云图可见,管道的冲蚀磨损主要集中在变径段B处,同时可以发现,变径段下部(重力方向)的磨损程度要远远大于管道上部的磨损情况,同时冲蚀磨损率随着颗粒直径的增大而继续增大。
(2)水流速度对管道冲蚀磨损的影响
给定相关参数,通过逐渐增大管道进口处的水流速度,得出水流速度与管道最大冲蚀磨损率的关系如图3所示。从图中可以看到,水流速度与管道的最大冲蚀率成反比趋势,这不同于前文的颗粒直径与冲蚀磨损率的关系。在低速水流条件下,管道的冲蚀磨损率要明显大于高速水流条件下的冲蚀磨损率。而因重力的影响,变径段B处底部的磨损同样也会大于顶部。
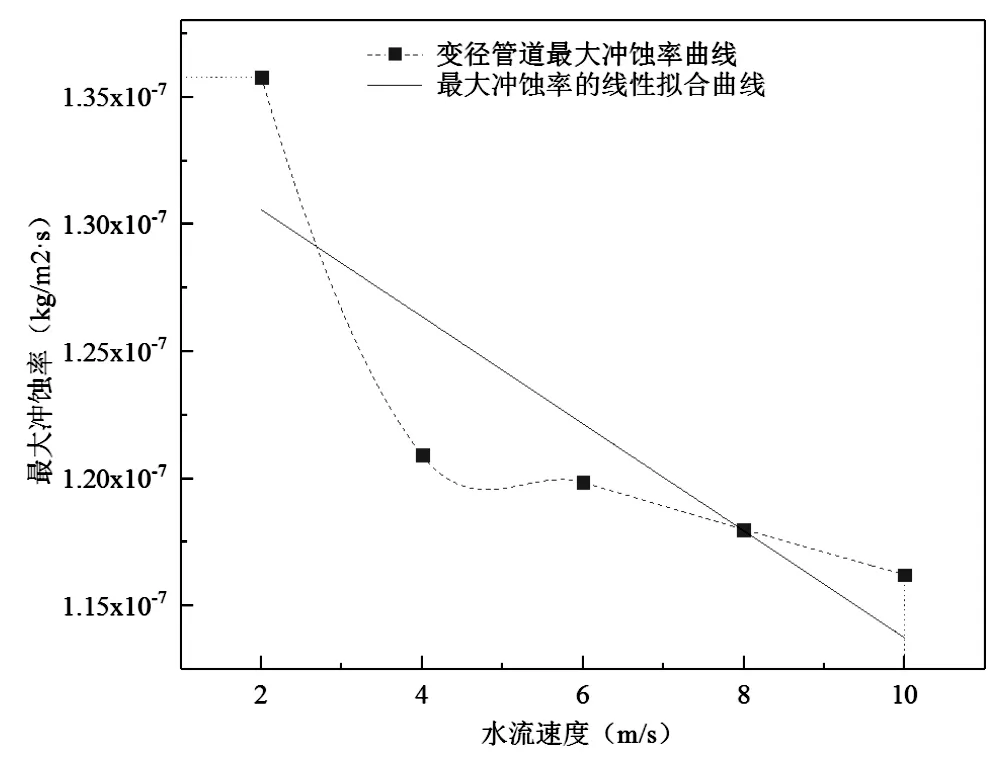
图3 不同水流速度与最大冲蚀磨损率的关系曲线
(3)最大冲蚀部位与防护
因变径管几何结构的原因,管道内的最大冲蚀磨损部位都出现在变径段B处,而变径段B处冲蚀最为严重的区域为底部(重力方向)。因此,管道的防护,应注意减小变径段B处的冲蚀磨损。可以采用诸如增大管道的水流速度及减小颗粒的大小等方法来对变径段进行防护。
4.结论
变径管道的最大冲蚀磨损率与颗粒直径及水流速度的关系如下:颗粒直径与管道的最大冲蚀磨损率成正比关系,而水流速度与最大冲蚀磨损率成反比关系。对于本文研究的液固两相流变径管道,因管道结构与液体流动的特点,最大冲蚀磨损部位均发生在变径段B处,因存在重力的作用,变径段B处磨损最严重的位置则出现在底部(重力方向)。

