读思达教学法下数学思想渗透的实践与思考——以“数学广角——集合”教学为例

张丽芳

（莆田市荔城区梅峰小学，福建 莆田 351100）

集合思想是数学中最基本的思想，虽然学生在计数和计算的学习中，已经接触过集合思想，但学生在低年级接触的集合思想更多是一一对应的思想，对于两个集合间的运算，尤其是交集和并集的体会并不多。本文结合人教版《义务教育教科书·数学》三年级上册第九单元“数学广角——集合”课堂教学实践，谈谈对本节课教学的一些实践与思考。

一、读情境，营造利于唤起求知欲的读思达课堂

古希腊著名科学家柏拉图说：“良好的开端是成功的一半。”教师在新课导入时，要根据教学内容，创设出有助于学生自主学习、合作交流的学习情境，从而激发他们的求知欲，真正把他们带入到最佳的学习状态。

在本课教学过程中，笔者设计了以下情境来导入新课：三年（2）班同学在迎元旦联欢会上有5 人参加合唱表演，有6 人参加小品表演，参加这两项表演的一共有多少人？创设这个情境，笔者并没有让学生马上得出参加这两项表演的一共有多少人？而是分三个层次让学生来解读情境，理解题意。

（一）了解信息，口算回答

让学生口算回答参加这两项表演的总人数为：5+6=11（人）。

（二）出示名单，引发认知冲突

课件出示三（2）班参加这两项表演学生名单的统计表，让学生观察参加这两项表演的总人数。

（三）出示座号，让学生再观察

课件出示三（2）班参加这两项表演的学生名单的座号，学生根据解读题意分析，得出参加这两项表演的总人数为9 人，发现其中有两位同学两项表演都有参加，从而得出重复或相近的意思。

在本课教学过程中，笔者让学生读出生活中熟悉的情境内容，发现有重复的人数，从而找准教学的起点，唤起学生的求知欲，让课堂教学变得更加有效。

二、思问题，营造利于体验解决方法多样性的读思达课堂

《义务教育数学课程标准（2011 年版）》要求：教师要充分发挥创造性，依据学生的年龄特性和知识水平，设计富有探索性和开放性的问题，给学生提供自主探索的机会。古语有云：“学起于思，思源于疑。”疑问是思维的动力，在课堂教学中，教师精心设计核心问题，把教师教授的主观愿望转化为学生学习的内在需要。

荷兰数学教育家弗赖登塔尔也曾强调：“学习数学的唯一正确的方法是实行‘再创造’”。本节课中，笔者充分遵循教学理论，围绕着“参加合唱和小品这两项表演共有多少人？”这个核心主问题，让学生自主探究韦恩图的由来，并在不同的策略中感受到解决问题方法的多样性，学生既获得了成功的体验，又经历利用集合思想来解决问题的过程。

在本节课，笔者让学生小组分工合作，思考用画图的方法或画表格来正确表示“参加合唱和小品这两项表演共有多少人？”，学生会得出不同的方法。笔者从中选出几种不同作品展示：

（一）方法一

合唱：翁艳青、翁燕燕、张宇

小品：叶飞霆、叶元浩、蔡秀婷、陈依星

两项都参加：翁家月、林凯宁

（二）方法二

两项都参加：⑧⑦

（三）方法三

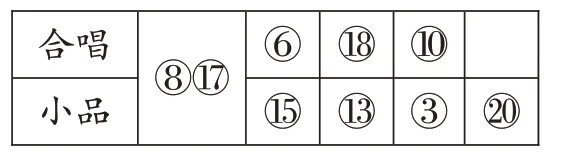
（四）方法四

（五）方法五

（六）方法六

在以上六种方法中，方法一和方法二都是用列举法来表示，其中方法二用座号表示更简单；方法三和方法四则是用表格的形式来表示，方法三中把⑧和○17放在中间便于观察而且能清楚地表示两项都参加的学生；方法五和方法六用椭圆来表示，把两项都参加的学生放在中间让人看了一目了然。日常中我们习惯用方法六来表示，方法六就是我们常说的维恩图，维恩图常用来研究表示数学中的“集合问题”，也叫集合图。对于这六种方法，笔者让学生再次思考：它们的异同点与优缺点？接着课件演示，让学生尝试正确表述集合图各部分的意义。学生据图列式计算出该班参加这两项表演的一共有多少人？算法一：5+6-2=9（人）；算法二：3+2+4=9（人）；算法三：5+4=9（人）；算法四：3+6=9（人）。在这里借助集合图，让学生弄清重叠问题中的数量关系，并适机渗透了数学集合思想，达到润物细无声的目的。

通过思考问题、合作探究、策略分析、反馈方法等途径，来使学生体验解决问题方法的多样化，激励学生思维，启发学生大胆、独立运用数学知识，营造有效课堂，促进学生创造力的提高。

三、达应用，营造利于解决生活问题的读思达课堂

拓展应用是学生学习过程中不可缺少的重要环节，也是学生掌握知识、形成技能、发展智力的重要手段。平时教学中，很多学生出现了“一看就懂，一说就会，一做就错”的现象。因此，如何破解这个难题，就需要教师在教学中根据教材内容的特点，围绕教学目标和学生实际。为此，笔者精心设计2 道有层次、针对、实效的表达应用，让学生在有效的课堂练习中形成数学技能，锻炼思维，发展智力，渗透数学集合思想。

（一）动物乐园

把下面动物的序号填写在合适的圈里。

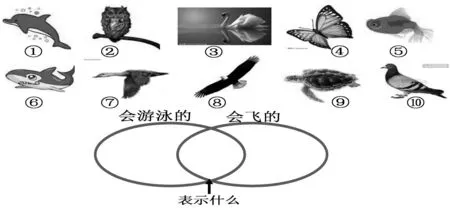
请同学们根据上图说一说:

1.只会游泳的有（）种动物；只会飞的有（）种动物；既会游泳又会飞的有（）种动物。

2.会游泳的或会飞的一共有（）种动物。

这一题要求学生根据集合元素的特征填写维恩图，第1 小题突出强调图中重合部分表示什么，让学生用语言表达“既会游泳又会飞的”，加深对交集含义的认识。第2 小题则用表达逻辑关系的语言“或”提出关于集合运算后的元素个数问题，让学生体会如何用生活语言表述两个集合的运算：并集。

（二）知识城堡

三年（1）班同学在迎元旦联欢晚会上有5 人参加合唱表演，有6 人参加小品表演，你觉得可能会有多少人参加这两项表演？最多会有几人？最少会有几人？

判断：

小军说：“每班参加这两项表演的同学最多有9人。”（）

林丽说：“每班参加这两项表演的同学最少有6人。”（）

这一题是创设情境中问题的延伸，笔者根据学生的回答，课件动态演示从不重复，依次重复1 人至5人参加两项比赛的情况，同时呈现算式：

本节课精心为学生设计了一组有梯度的课堂练习，从简单应用到开放，从正向思维到逆向思维，既链接所学知识资源，又实现对学生思维的拓展。这样的练习设计不仅能让学生在有效的课堂教学中结合集合思想进行分析，同时使学生始终处于积极的思考、交流和感悟之中，增强了学习数学的信心。

总之，在“数学广角——集合”的有效教学过程中，充分渗透数学集合思想，体现了以学生为本，让学生经历数学知识的形成过程，感悟数学的价值，使学生获得全面的进步与发展。