风险视角下的动车组部件预防性维修博弈优化
熊律, 王红, 蒋祖华
(1.兰州交通大学 机电工程学院,甘肃 兰州 730070; 2.广东交通职业技术学院 轨道交通学院,广东 广州 510650; 3.上海交通大学 机械与动力工程学院,上海 200240)
由于受到各自绩效的影响,企业中各部门存在潜在竞争关系。例如,大型制造企业中的生产方和维修方,生产方希望尽量减少设备的停机时间以满足生产需求,维修方为了保证生产设备安全可靠地运行会制定出一份详尽的维修计划,显然,二者之间存在某种利益竞争。近年来,采用博弈理论来解决生产实际中的经济学问题成为学者们研究的一个热点[1-5]。博弈理论在企业经营决策[6]、电力定价[7]和农地增值分配[8]等领域有着十分广泛的应用。丁珮雯[9]将博弈理论应用到预防性维修(PM)和生产调度的联合优化研究之中,解决了生产方和维修方在利益相互干涉的情况下,使得双方的收益达到最优;Hu等[10]以生产计划部门和维修部门作为博弈参与者,采用Stackelberg博弈模型来协调生产计划和PM计划之间的内在干涉问题;段华薇等[11]为得出传统快递与高铁快递合作的最优定价策略,分析主导权及市场需求波动对其影响,根据双方构成供应链的特点,基于2种随机市场需求函数分别构建了高铁快递和传统快递主导下的Stackelberg博弈模型;王红等[12]认为在地铁车辆的维修决策过程中,各部门之间存在隐形的利益竞争,为了探讨这种隐形竞争对车辆设备PM计划的影响,论文基于动态博弈理论,以地铁车辆运营方和维修方为参与者,分别建立了运营优先和维修优先的Stackelberg博弈模型;詹文杰等[13]通过建立“双种群”复制动态模型,研究了有限理性假设下“多对多”讨价还价策略演化问题,证明了只有严格纳什均衡才能成为“多对多”讨价还价的演化稳定策略。以上文献在争取博弈双方经济效益最优化方面做出了贡献,然而,有时候在追求经济效益最优化的同时,把风险控制在合理的、可以接受的范围内也是学者们追求的关键目标。例如,动车组检修行业,随着铁路行业市场化进程的加快,如何在满足动车组安全可靠运行(低运行风险)的大前提下,尽量降低动车组的检修费用是一个值得深入探讨的问题。作为保障动车组安全有序运营的2个重要部门,动车组的运营方和维修方具有天然的博弈协作关系。作为运营方,它期望动车组可以以最低的风险水平,把乘客安全舒适地送达目的地。而作为维修方,则期望在保证动车组具有一定的可靠性的前提下,可以尽量地降低维修成本。然而,由文献[14]可知,部件的PM可靠度阈值越高,则部件在一个寿命周期内的PM成本越高,部件的故障次数越少,从而运行风险越低;反之,部件的PM可靠度阈值越低,其PM成本越低,则一个寿命周期内对其实施的PM次数越少,部件的故障次数越多,从而导致运行风险增加。如何平衡动车组部件维修成本和故障风险的分配,实现双方利益的均衡是本文研究的重点。
本文首先对动车组部件现行的PM机制作了基本的问题描述和假设。其次,基于我国动车组维修方现行的分级检修机制,对两级非完美维修策略的故障率演化规则进行了详细阐述,并对影响动车组部件故障风险的因素进行评分和权重,建立动车组部件故障风险评价函数。然后,以动车组运营方和维修方作为博弈参与者,建立了基于故障风险的动车组部件3阶段讨价还价PM博弈模型。最后对运营方优先出价和维修方优先出价的优化结果进行对比分析并得出结论。
1 问题描述与假设
本文以CRH3系列动车组在四级修程时进行更换的部件为研究对象。由CRH3系列动车组的检修制度可知,每20 000 km就会对整车进行检修,因此选择偶数里程对部件进行维修就可以确保部件的维修时机是选择在动车组整车的检修时机时执行的,即部件的维修时机为li=2n,其中,i=1,2,…,N-1,n=1,2,…,N-1,从li-1到li为部件的第i个PM周期。此外,CRH3系列动车组四级修时,某些部件需要进行更换,更换属于完美维修[15-16]。部件在里程区间(l0,lmax)内共进行了N-1次PM,在第N次PM时刻,即动车组运行到lmax时对部件进行更换。
对论文作如下假设:
1) 部件从全新状态开始工作;
2) 当部件发生非预期故障时采用故障维修方式,故障维修不改变部件的故障率;
3) 初级维修和高级维修均属于非完美维修方式,即可在一定程度改善部件的故障率,但不能使部件修复如新。
2 模型的建立
2.1 故障率演化规则
Lin等[17]综合役龄递减模型[18]和故障率递增模型[19]的优势,提出了一种混合PM模型,其故障率表达式为:
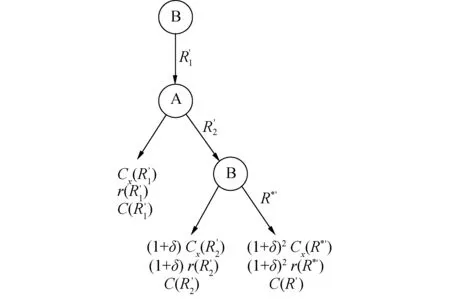
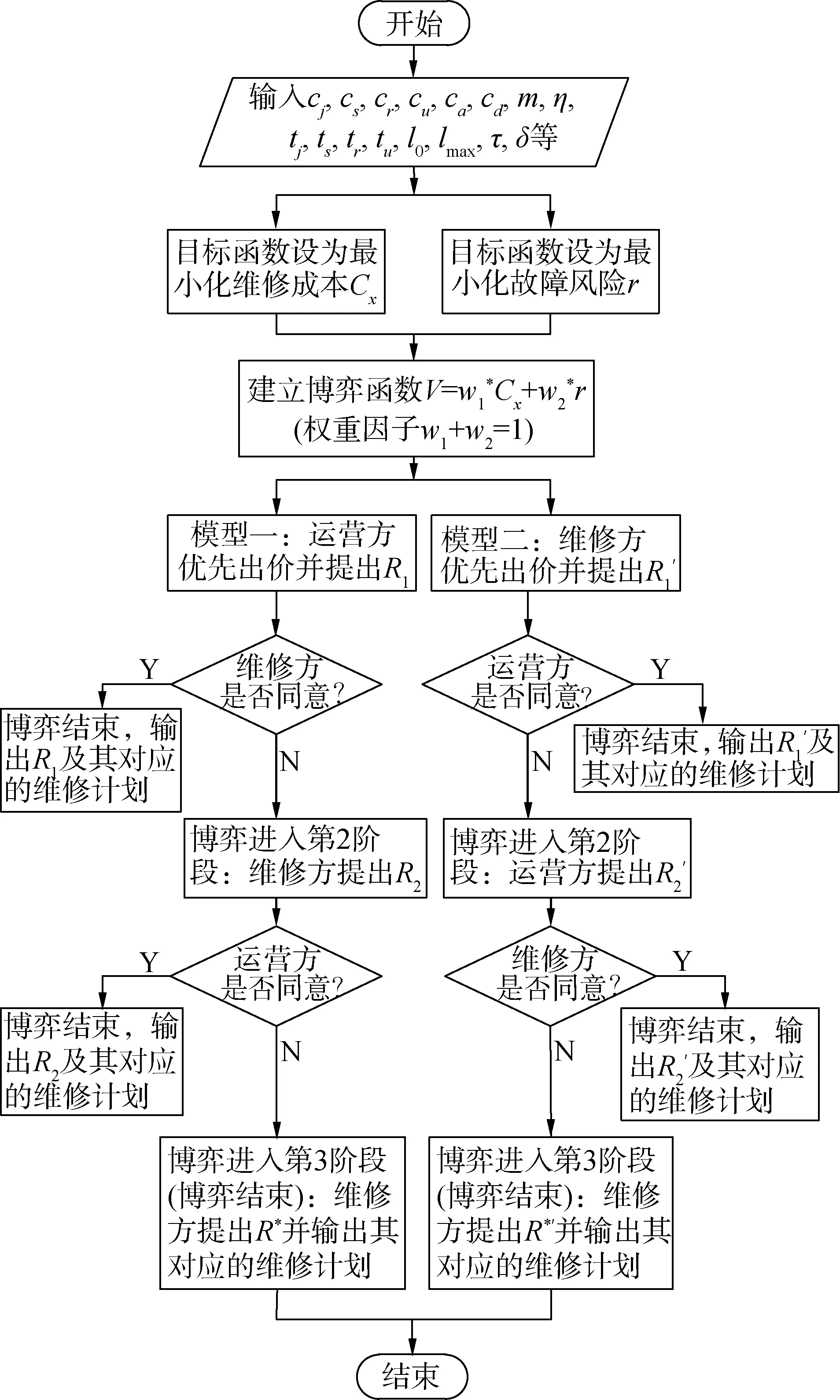
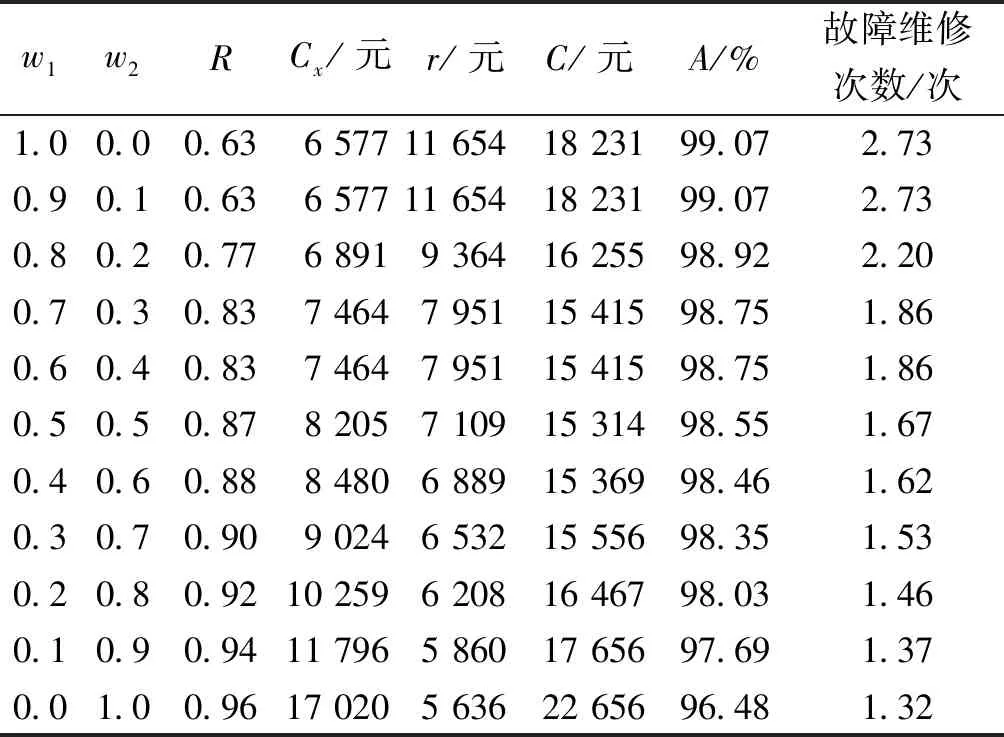
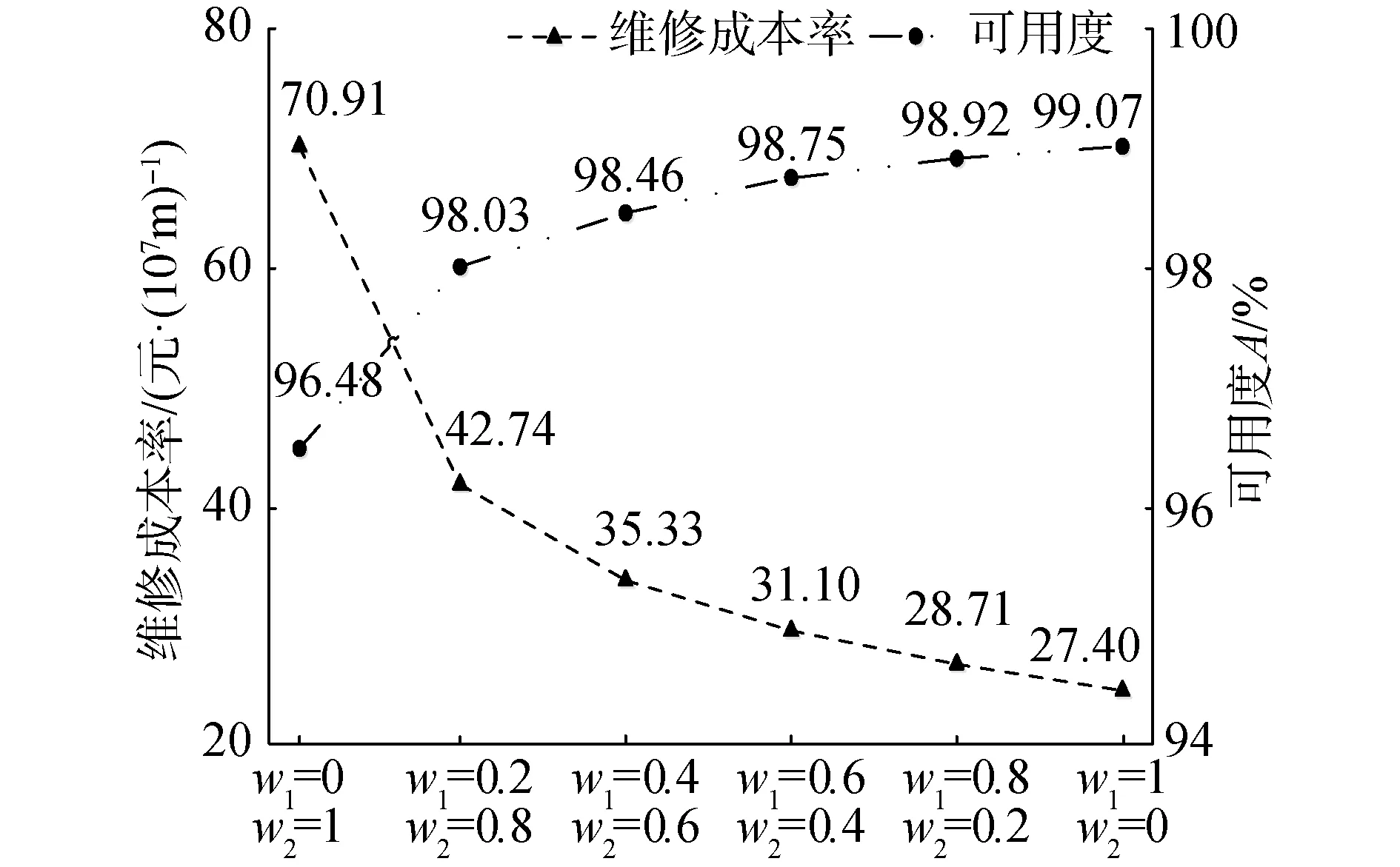
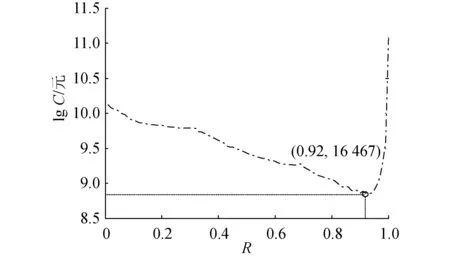
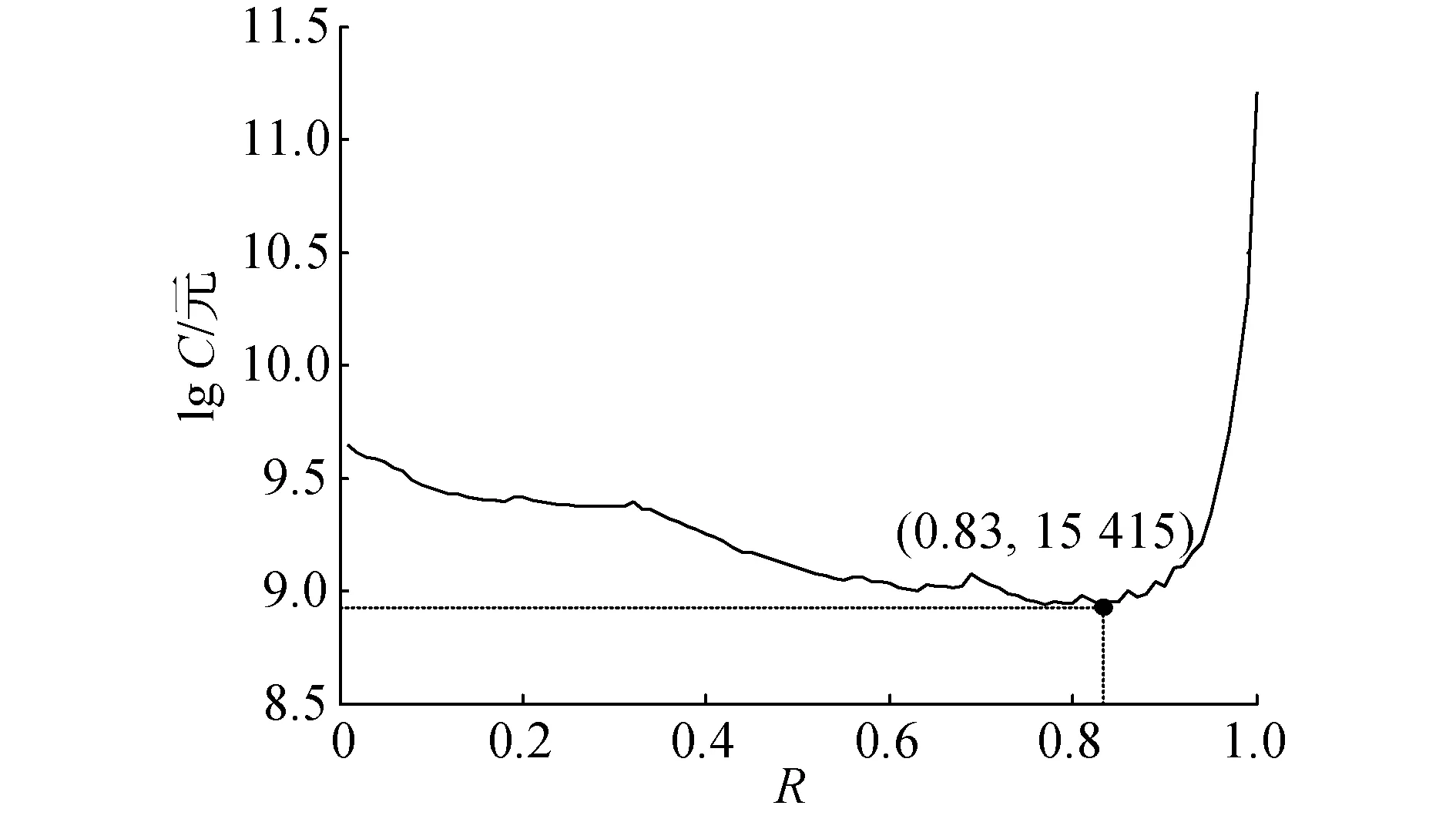
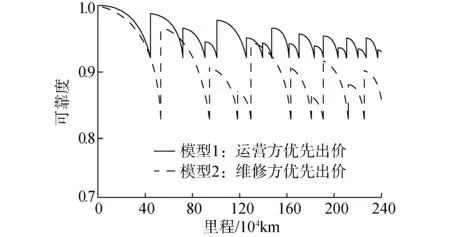
λi+1(l)=biλi(l+aiLi) 0 (1) 式中:λi为部件第i个PM周期的故障率函数;Li为部件第i-1次与第i次PM的里程间隔,且有Li=li-li-1;ai为役龄递减因子;bi为故障率递增因子。部件的维修方式采用两级非完美PM策略,其故障率演化规则如图1所示。 以υi表示部件的PM方式: (2) 则ai和bi可分别表示为: (3) (4) 图1 两级非完美故障率演化规则Fig.1 Failure rate evolution rule of bi-level imperfect PM (5) (6) (7) 式中:cj为初级维修成本;as为高级维修成本。 式(2)可表示为: (8) 本文以动车组运行安全性、动车组晚点以及维修的难易程度[20-21]作为影响动车组部件故障风险的评价因素。 故障风险因子ψ可表示为: (9) 式中:sk表示对影响因素的评分;σk表示影响因素的权重;n表示影响因素的个数。 参照文献[22]对设备重要度的评价方法,对动车组部件的故障风险进行量化分析。 首先,对各影响因素进行评分,其评分标准如表1所示。 其次,需要确定各影响因素的权重。对于各决定因素权重的确定,可参照文献[23-25]采用层次分析法求得。 表1 各影响因素的评分标准Table 1 Scoring criteria for each influence factors 最后,部件的故障风险表达式可表示为: (10) 式中cd表示单位故障风险成本。 根据本文的维修策略,当部件到达PM时机时,对部件执行PM维修;若部件发生非预期故障则对部件执行故障维修;当部件运行到达lmax时,对部件执行更换操作。部件在一个更换周期内的维修成本主要由:PM成本、故障维修成本和更换成本3部分组成。 1) PM成本。 (11) (12) (13) 2) 故障维修成本。 故障维修旨在恢复部件的功能,使其保持运行状态。当动车组部件出现非预期故障时,对其执行故障维修。故障维修成本Cr表达式为: (14) 式中:cr为故障维修成本;ti为故障维修时间。 3) 故障维修惩罚成本。 当部件在工作过程中出现非预期故障时,故障修复时间越短越好。以tj表示故障修复时间的最大允许值,如果在tj时间段内故障无法消除,就要产生故障维修惩罚。用cb表示小修时间超过tj后单位时间的惩罚成本,则部件故障惩罚成本为: (15) 4) 更换成本。 当动车组部件到达四级维修时机时,对其执行更换操作。更换成本包括更换操作成本cu和浪费成本ca。 Cg=cu+ca+τtu (16) 式中λu为更换操作时间。 综上可知,维修成本可表示为: Cx=Cp+Cr+Cd+Cg (17) 维修成本率可表示为: (18) 部件在一个更换周期内的总成本包括2部分,维修成本和风险成本,其表达式为: C=Cx+r (19) 通过优化部件在一个更换周期内的总成本可以得到部件最终的PM计划。 将动车组预防性维修和故障维修的时间以300 km/h换算成里程数,从而可将动车组部件一个寿命周期内的可用度表示为: (20) 讨价还价是有共同利益的参与人面临冲突时试图达成一致的一种博弈过程,它是一种典型的谈判活动:谈判过程中当对方的报价连同主要的合同条款向己方提出后,己方对其全部内容进行分析,通过对方的报价来判断对方的意图,并给予再报价等反应,使交易朝着即对己方有利又满足对方某些要求的方向发展,以有利于最终实现谈判中的利益交换。 对于讨价还价博弈模型,由于需要消耗一定的谈判费用和谈判时间,每当谈判进行到下一个回合,双方的成本函数都要在原基础上额外增加一个损失系数δ(0<δ<1)[3]。 为了表征维修成本和风险成本在总成本中所占的比例不同对动车组部件PM计划的影响,引入维修成本权重w1和风险成本权重w2。加权总成本表达式为: V=w1Cx+w2r (21) 模型1:运营方优先出价,博弈过程如图2。 图2 模型1博弈过程Fig.2 Game process of the first model 双方博弈过程如下: 1)运营方以min(r)为决策目标,优化得到R1; 2)维修方选择接受或者拒绝。若维修方接受,则博弈结束,此时,维修成本为Cx(R1),风险成本为r(R1),总成本为C(R1);若维修方拒绝,则由维修方优化得到R2; 3)运营方选择接受或者拒绝。若运营方接受,则博弈结束,此时维修成本为(1+δ)Cx(R2),风险成本为(1+δ)r(R2),总成本为C(R2);若运营方拒绝,则由运营方优化得到R*,此时,维修方必须接受,博弈结束。则维修成本为(1+δ)2Cx(R*),风险成本为(1+δ)2r(R*),总成本为C(R*)。 模型2:维修方优先出价,博弈过程如图3。 图3 模型2博弈过程Fig.3 Game process of the second model 双方博弈过程如下: 1) 模型1的求解方法。 Round 1:运营方通过优化目标函数min(r),得到对其较有利的R1值。维修方可以选择接受或者拒绝,若接受,则博弈结束;反之,维修方提出R2。 Round 2:博弈进入到第2回合R2需满足条件: (1+δ)Cx(R2) (22) Round 3:博弈进入到第3回合R*需满足条件: (1+δ)2r(R*)<(1+δ)r(R2) 且(1+δ)2C(R*)<(1+δ)C(R2) (23) 2) 模型2的求解方法。 (24) Round 3:博弈进入到第3回合R*′需满足条件: (25) 风险视角下的动车组部件PM博弈算法流程如图4所示。首先输入系统参数,并以维修成本和故障风险为优化目标建立博弈函数V。然后,以运营方优先出价和维修方优先出价分别建立3阶段讨价还价博弈模型。3阶段讨价还价博弈的特点是只要任何一方接受另一方的方案,博弈就结束,并且博弈过程只能进行3个回合。最后,根据2种博弈模型的优化结果得出PM可靠度阈值R作为最优解,并输出其对应的PM计划。 图4 算法流程Fig.4 The algorithm flow chart 动车组部件的故障率函数服从威布尔分布,其表达式为λ1(l)=(m/η)(l/η)m-1。威布尔分布的参数m和η,可通过收集整理部件的寿命数据,进而通过寿命数据分析求得。取部件的形状参数m=3,尺度参数η=100。 其他维修参数如表2所示。 表2 维修参数Table 2 Maintenance parameters 表3是在w1和w2分别取不同值的情况下,部件的PM优化结果。图5是不同权重分配下的部件的维修成本率和可用度结果对比。 表3不同权重分配下的PM优化结果 Table3PMoptimizationresultswithdifferentweightcoefficients w1w2RCx/元r/元C/元A/%故障维修次数/次1.00.00.636 57711 65418 23199.072.730.90.10.636 57711 65418 23199.072.730.80.20.776 8919 36416 25598.922.200.70.30.837 4647 95115 41598.751.860.60.40.837 4647 95115 41598.751.860.50.50.878 2057 10915 31498.551.670.40.60.888 4806 88915 36998.461.620.30.70.909 0246 53215 55698.351.530.20.80.9210 2596 20816 46798.031.460.10.90.9411 7965 86017 65697.691.370.01.00.9617 0205 63622 65696.481.32 图5 不同权重分配下的维修成本率和可用度Fig.5 Maintenance cost rate and availability with different weight coefficients 由表3中优化结果可知: R值的优化结果随着w1的变大而减小,随着w2的变大而增大;Cx随着w1的变小而增大,随着w2的变小而减小;r随着w1的变小而减小,随着w2的变小而增大;可用度A和故障维修次数随着w1的变小而减小,随着w2的变小而增大。 当w1=0.0,w2=1.0时,风险成本r最低,但是维修成本Cx却很高,所以总成本C并非最低;当w1=1.0,w2=0.0时,维修成本Cx最低,但是风险成本r却很高,故总成本C依然较高;当w1=0.5,w2=0.5时,维修成本Cx和风险成本r虽然都不是最低,但总成本C最低。 由图5可知,部件的维修成本率随着w1的增大而减小,随着w2的增大而增大;部件的可用度随着w1的变大而上升,随着w2的变大而降低。 图6和图7分别给出了运营方优先出价和维修方优先出价情况下的总成本C随R值增加的变化曲线。 图6 运营方优先出价情况下的lgC-R曲线Fig.6 lgC-R curve of operation sector priority bid 图7 维修方优先出价情况下的lgC-R曲线Fig.7 lgC-R curve of maintenance sector priority bid 由图6和图7可以看出,部件在一个PM周期内的总成本C随R值的增加呈现先减小后增加的趋势,在某一R值处总成本C达到最低,这个最低点即为我们所求的最优点。 表4是2种博弈模型的优化结果,表5是2种博弈模型下部件的PM计划。 由表4和表5可知: 在3阶段讨价还价博弈规则下,运营方优先出价(模型1)的R值优化结果高于维修方优先出价(模型2),并且其故障维修次数相比于模型二降低了21.5%,这说明运营方对部件的可靠度有着更高的要求。 图8 2种博弈模型的可靠度演化对比Fig.8 Reliability evolution comparison between the two models 模型1风险成本的优化结果要低于模型2,模型2维修成本的优化结果要低于模型1。这是由于运营方期望动车组的运营风险较低,而维修方期望动车组的维修成本较低,2种博弈模型的优化结果基本符合二者的期望。这也说明优先出价方具有优势,即博弈的结果更有利于优先出价方。 模型1相比于模型2多执行了4次初级维修和3次高级维修,这意味着模型1需要更多次的停机来执行PM计划,故模型1的可用度低于模型2。同时,模型1会导致更高的维修成本率,并且其总成本也高于模型2。 表4 2种博弈模型的优化结果Table 4 Optimization results of the two game models 表5 2种博弈模型下的PM计划(0-初级维修, 1-高级维修)Table 5 PM shedules under the two game models(0-junior maintenance, 1-senior maintenance) 无论是模型1还是模型2,部件在前半个更换周期(0~120×104km)的非完美PM措施采用的都是初级维修,而高级维修都是在部件更换周期的后半阶段(120×104~240×104km)执行的。 1) 运营方优先出价的情况下,部件在一个寿命周期内的可用度较低,维修成本率较高,但可使部件保持更高的可靠度水平,尤其在部件寿命周期的后半阶段。并且其非预期故障发生概率相比于维修方优先出价情况下降低了约21.5%。 2) 在两级非完美PM策略下,部件在前半个更换周期内采取初级维修即可满足可靠度要求,而在部件更换周期的后半阶段,有必要采取一定次数的高级维修措施以保证动车组部件的可靠度水平保持在合理水平。 3) 在三阶段讨价还价博弈模型中,博弈的结果更有利于优先出价的一方。故为了在博弈过程中占据主动,博弈双方应尽量争取优先出价权。 4) 文中对动车组部件的非完美维修策略采用的是两级非完美PM策略,然而,在动车组以及其他生产设备的维修实际中,针对部件的状态和性能阶段不同,往往有多种维修手段与之对应。下一步研究可将对动车组部件的非完美维修策略延展到多级非完美维修。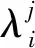
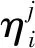

2.2 维修方式选择

2.3 故障风险评价函数建模

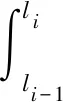
2.4 维修成本建模

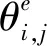
2.5 总成本建模
2.6 可用度建模
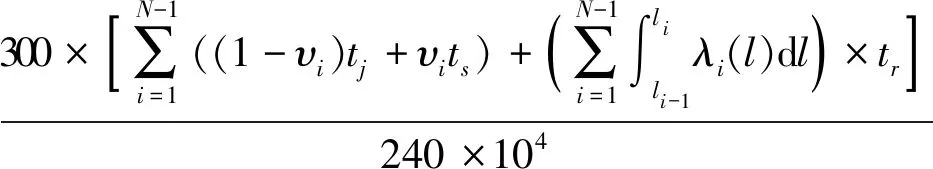
3 三阶段讨价还价博弈模型
3.1 模型的建立

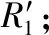
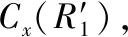
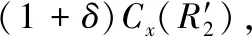
3.2 模型的求解
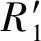
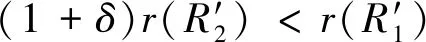

3.3 算法流程图
4 实例分析



5 结论

